6.1.1 分类加法计数原理与分步乘法计数原理-2022-2023学年高二数学同步精讲课件(共28张PPT)(人教A版2019选择性必修第三册)
文档属性
| 名称 | 6.1.1 分类加法计数原理与分步乘法计数原理-2022-2023学年高二数学同步精讲课件(共28张PPT)(人教A版2019选择性必修第三册) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-22 14:15:42 | ||
图片预览








文档简介
直线
6.1 .1 分类加法计数原理与分步乘法计数原理
问题导入
l
l
思考1:用一个大写的英文字母或一个阿拉伯数字给教室里的一个座位编号,总共能编出多少种不同的号码?
l
计数问题是我们从小就经常遇到的,通过列举一个一个地数是计数的基本方法.但当问题中的数量很大时,列举的方法效率不高.能否设计巧妙的“数法”,以提高效率呢?下面先分析一个简单的问题,并尝试从中得出巧妙的计数方法.
因为英文字母共有26个,阿拉伯数字共有10个,所以总共可以编出
26+10=36种不同的号码.
?
新知探索
l
l
问题1:你能说一说这个问题的特征吗?
l
首先,这里要完成的事情是“给一个座位编号”;其次是“或”字的出现:一个座位编号用一个英文字母或一个阿拉伯数字表示.因为英文字母与阿拉伯数字互不相同,所以用英文字母编出的号码与用阿拉伯数字编出的号码也互不相同.这两类号码数相加就得到了号码的总数.
上述计数过程的基本环节是:
(1)确定分类标准,根据问题条件分为字母号码和数字号码两类;
(2)分别计算各类号码的个数;
(3)各类号码的个数相加,得出所有号码的个数.
新知探索
l
l
l
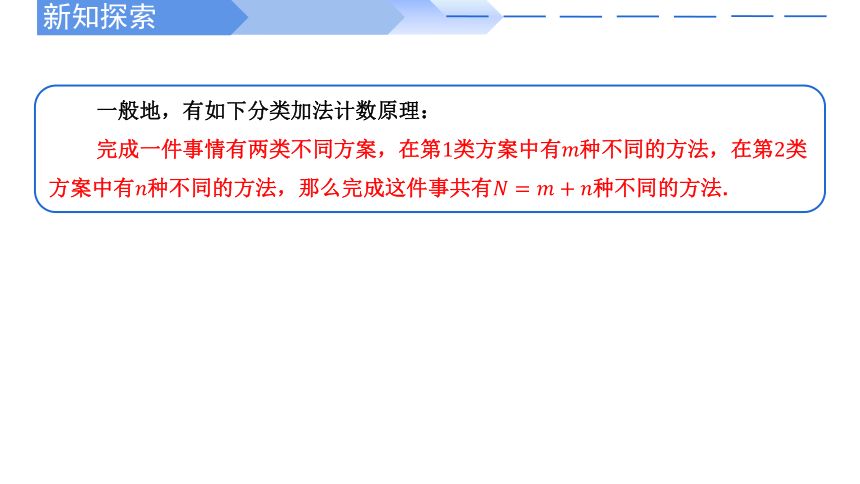
一般地,有如下分类加法计数原理:
完成一件事情有两类不同方案,在第1类方案中有????种不同的方法,在第2类方案中有????种不同的方法,那么完成这件事共有????=????+????种不同的方法.
?
例析
例1.在填写高考志愿表时,一名高中毕业生了解到,????,????两所大学各有一些自己感兴趣的强项专业,如表.如果这名同学只能选一个专业,那么他共有多少种选择?
?
l
解:这名同学可以选择????,????两所大学中的一所.在????大学中有5种专业选择方法,在????大学中有4种专业选择方法.因为没有一个强势专业是两所大学共有的,所以根据分类加法计数原理,这名同学可能的专业选择种数为:????=5+4=9.
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}????大学
????大学
生物学
数学
化学
会计学
医学
信息技术学
物理学
法学
工程学
新知探索
l
l
问题2:如果完成一件事有三类不同方案,在第1类方案中有????1种不同的方法,在第2类方案中有????2种不同的方法,在第3类方案中有????3种不同的方法,那么完成这件事共有多少种不同的方法?
如果完成一件事有????类不同方案,在每一类方案中都有若干种不同的方法,那么应当如何计数呢?
?
l
思考2:用前6个大写英文字母和1~9这9个阿拉伯数字,以????1,????2,…,????9,????1,
????2,…的方式给教室里的一个座位编号,总共能编出多少种不同的号码?
?
新知探索
l
l
这里要完成的事情仍然是“给一个座位编号”,但与前一问题的要求不同.在前一问题中,用26个英文字母中的任意一个或10个阿拉伯数字中的任意一个,都可以给出一个座位号码.但在这个问题中,号码必须由一个英文字母和一个作为下标的阿拉伯数字组成,即得到一个号码要经过先确定一个英文字母,后确定一个阿拉伯数字这样两个步骤.用如图所示的方法可以列出所有可能的号码.
l
新知探索
l
l
也可能这样思考:由于前6个英文字母中的任意一个都能与9个数字中的任意一个组成一个号码,而且它们互不相同,因此共有6×9=54种不同的号码.
?
l
问题3:你能说一说这个问题的特征吗?
上述问题要完成的一件事情仍然是“给一个座位编号”,其中最重要的特征是“和”字的出现:一个座位编号由一个英文字母和一个阿拉伯数字构成.因此得到一个座位号要经过先确定一个英文字母,后确定一个阿拉伯数字这两个步骤,每一个英文字母与不同的数字组成的号码是互不相同的.
新知探索
l
l
l
一般地,有如下分步乘法计数原理:
完成一件事需要两个步骤,做第1步有????种不同的方法,在第2步有????种不同的方法,那么完成这件事共有????=????×????种不同的方法.
?
例析
例2.某班有男生30名、女生24名,从中任选男生和女生各1名代表班级参加比赛,共有多少种不同的选法?
?
l
解:第1步,从30名男生中选出1人,有30种不同选法;第2步,从24名男生中选出1人,有24种不同选法.根据分步乘法计数原理,共有不同选法的种数为????=30×24=720.
?
问题4:如果完成一件事需要三个步骤,做第1步有????1种不同的方法,做第2步有????2种不同的方法,做第3步有????3种不同的方法,那么完成这件事共有多少种不同的方法?
如果完成一件事有????类不同方案,做每一步都有若干种不同的方法,那么应当如何计数呢?
?
例析
例3.书架的第1层放有4本不同的计算机书,第2层放有3本不同的文艺书,第3层放有2本不同的体育书.
(1)从书架上任取1本书,有多少种不同取法?
(2)从书架的第1层、第2层、第3层各取1本书,有多少种不同取法?
l
解:(1)从书架上任取1本书,有三类方案:第1类方案是从第1层取1本计算机书,有4种方法;第2类方案是从第2层取1本文艺书,有3种方法;第3类方案是从第3层取1本体育书,有2种方法.根据分类加法计数原理,不同取法的种数为
????=4+3+2=9.
?
例析
例3.书架的第1层放有4本不同的计算机书,第2层放有3本不同的文艺书,第3层放有2本不同的体育书.
(1)从书架上任取1本书,有多少种不同取法?
(2)从书架的第1层、第2层、第3层各取1本书,有多少种不同取法?
l
解:(2)从书架的第1层、第2层、第3层各取1本书,可以分三个步骤完成:第1步,从第1层取1本计算机书,有4种方法;第2步,从第2层取1本文艺书,有3种方法;第3步,从第3层取1本体育书,有2种方法.根据分步乘法计数原理,不同取法的种数为????=4×3×2=24.
?
新知探索
答案:√,×,×,√.
辨析1.判断正误.
(1)在分类加法计数原理中,每类方案中的方法都能完成这件事.( )
(2)在分类加法计数原理中,两类不同方案中的方法可以相同.( )
(3)在分步乘法计数原理中,事情是分两步完成的,其中任何一个单独的步骤都能完成这件事.( )
(4)在分步乘法计数原理中,每个步骤中完成这个步骤的方法是各不相同的.( )
新知探索
辨析2.从3名女同学和2名男同学中选出一人主持本班一次班会,则不同的选法种数为( ).
A.6 B.5 C.3 D.2
?
答案:B.
辨析3.某商城共有4个门,购物者若从任意一个门进,从任意一个门出,则不同走法的种数是________.
?
答案:16.
练习
题型一:分类加法计数原理
例1.在所有的两位数中,个位数字大于十位数字的两位数的个数为_______.
解:(解法一)根据题意,将十位上的数字按1,2,3,4,5,6,7,8的情况分成8类,在每一类中满足题目条件的两位数分别是8个,7个,6个,5个,4个,3个,2个,1个.根据分类加法计数原理,符合条件的两位数的个数为8+7+6+5+4+3+2+1=36.
?
练习
例1.在所有的两位数中,个位数字大于十位数字的两位数的个数为_______.
解:(解法二)分析个位数字,可分以下几类:
个位是9,则十位可以是1,2,3,?,8中的一个,故共有8个;
个位是8,则十位可以是1,2,3,?,7中的一个,故共有7个;
同理,个位是7的有6个;?个位是2的有1个.
根据分类加法计数原理,符合条件的两位数的个数为8+7+6+5+4+3+2+1=36.
?
练习
方法技巧:
利用分类加法计数原理时的解题流程
(1)分类:将完成这件事的方法分成若干类.
(2)计数:求出每一类的方法数.
(3)结论:将每一类的方法数相加得出结果.
[提醒]确定分类标准时要确保每一类都能独立的完成这件事.
练习
变1.某校高三共有三个班,其各班人数如下表:
(1)从三个班中选一名学生担任学生会主席,有多少种不同的选法?
解(1):从三个班中任选一名学生,可分三类.
第一类,从1班任选一名学生,有50种不同选法;
第二类,从2班任选一名学生,有60种不同选法;
第三类,从3班任选一名学生,有55种不同选法.
根据分类加法计数原理,不同的选法的种数为????=50+60+55=165.
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}班级
男生人数
女生人数
总人数
高三1班
30
20
50
高三2班
30
30
60
高三3班
35
20
55
练习
变1.某校高三共有三个班,其各班人数如下表:
(2)从1班、2班、3班男生中或从3班女生中选一名学生担任学生会生活部部长,有多少种不同的选法?
解(2):由题设知共有三类方案.
第一类,从1班男生中任选一名学生,有30种不同选法;
第二类,从2班男生中任选一名学生,有30种不同选法;
第三类,从3班女生中任选一名学生,有20种不同选法.
根据分类加法计数原理,不同的选法的种数为????=30+30+20=80.
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}班级
男生人数
女生人数
总人数
高三1班
30
20
50
高三2班
30
30
60
高三3班
35
20
55
练习
题型二:分步乘法计数原理
例2.从?2,?1,0,1,2,3这六个数字中任选3个不重复的数字作为二次函数????=????????2+????????+????的系数????,????,????,则可以组成抛物线的条数为多少?
?
解:由题意知????不能为0,故????的值有5种选法;????的值有5种选法;????的值有4种选法.根据分步乘法计数原理,可以组成抛物线的条数为5×5×4=100.
?
练习
方法技巧:
利用分步乘法计数原理时的解题流程
(1)分步:将完成这件事的方法分成若干步.
(2)计数:求出每一步的方法数.
(3)结论:将每一步的方法数相乘得最终结果.
[提醒]分步时要注意不能遗漏步骤,否则就不能完成这件事.
练习
变2.从?2,?1,0,1,2,3这六个数字中任选2个作为椭圆????2????+????2????=1的参数????,????,则可以组成椭圆的个数是多少?
?
解:据条件知????>0,????>0,且????≠????,故需分两步完成,第一步确定????,有3种方法,第二步确定????,有2种方法,根据分步乘法计数原理可以组成椭圆的个数为3×2=6.
?
练习
题型三:两个计数原理的简单综合应用
例3.王华同学有课外参考书若干本,其中有5本不同的外语书,4本不同的数学书,3本不同的物理书,他欲带参考书到图书馆阅读.
(1)若他从这些参考书中带1本去图书馆,有多少种不同的带法?
(2)若带外语、数学、物理参考书各1本,有多少种不同的带法?
解(1):要完成的事情是带1本参考书,无论是带外语书,还是带数学书、物理书,事情都可完成,从而根据分类加法计数原理,不同带法的种数为5+4+3=12.
?
解(2):要完成的事情是带3本不同学科的参考书,只有从外语、数学、物理书中各选1本后,才能完成这件事,因此根据分步乘法计数原理,不同带法的种数为5×4×3=60.
?
练习
方法技巧:
利用两个计数原理解题时的三个注意点
(1)当题目无从下手时,可考虑要完成的这件事是什么,即怎样做才算完成这件事,然后给出完成这件事的一种或几种方法,从这几种方法中归纳出解题方法.
(2)分类时标准要明确,做到不重不漏,有时要恰当画出示意图或树状图,使问题的分析更直观、清楚,便于探索规律.
(3)综合问题一般是先分类再分步.
练习
变3.某电视台的主持人在某综艺节目中拿出两个信箱,其中放着竞猜中成绩优秀的观众来信,甲箱中有30封,乙箱中有20封,现由主持人抽奖确定幸运观众,若先从中确定一名幸运之星,再从两箱中各确定一名幸运观众,则有多少种不同结果?
解:①若幸运之星在甲箱中抽取,
不同结果的种数为30×29×20=17400;
②若幸运之星在乙箱中抽取,
不同结果的种数为20×19×30=11400.
故不同结果的种数为17400+11400=28800.
?
课堂小结
1.分类加法计数原理:
(1)任务:完成一件事;
(2)分类:有两类不同方案,在第1类方案中有????种不同的方法,在第2类方案中有????种不同的方法;
(3)计数:完成这件事共有????=????+????种不同的方法.
[注]????=????1+????2+????3+?+????????.
?
课堂小结
2.分类乘法计数原理:
(1)任务:完成一件事;
(2)分类:需要两个步骤,做第1步有????种不同的方法,做第2步有????种不同的方法;
(3)计数:完成这件事共有????=????×????种不同的方法.
[注]????=????1×????2×????3×?×????????.
?
作业
(1)整理本节课的题型;
(2)课本P5-—P6的练习1——4题;
(3)课本P11习题6.1的第1——6题.
6.1 .1 分类加法计数原理与分步乘法计数原理
问题导入
l
l
思考1:用一个大写的英文字母或一个阿拉伯数字给教室里的一个座位编号,总共能编出多少种不同的号码?
l
计数问题是我们从小就经常遇到的,通过列举一个一个地数是计数的基本方法.但当问题中的数量很大时,列举的方法效率不高.能否设计巧妙的“数法”,以提高效率呢?下面先分析一个简单的问题,并尝试从中得出巧妙的计数方法.
因为英文字母共有26个,阿拉伯数字共有10个,所以总共可以编出
26+10=36种不同的号码.
?
新知探索
l
l
问题1:你能说一说这个问题的特征吗?
l
首先,这里要完成的事情是“给一个座位编号”;其次是“或”字的出现:一个座位编号用一个英文字母或一个阿拉伯数字表示.因为英文字母与阿拉伯数字互不相同,所以用英文字母编出的号码与用阿拉伯数字编出的号码也互不相同.这两类号码数相加就得到了号码的总数.
上述计数过程的基本环节是:
(1)确定分类标准,根据问题条件分为字母号码和数字号码两类;
(2)分别计算各类号码的个数;
(3)各类号码的个数相加,得出所有号码的个数.
新知探索
l
l
l
一般地,有如下分类加法计数原理:
完成一件事情有两类不同方案,在第1类方案中有????种不同的方法,在第2类方案中有????种不同的方法,那么完成这件事共有????=????+????种不同的方法.
?
例析
例1.在填写高考志愿表时,一名高中毕业生了解到,????,????两所大学各有一些自己感兴趣的强项专业,如表.如果这名同学只能选一个专业,那么他共有多少种选择?
?
l
解:这名同学可以选择????,????两所大学中的一所.在????大学中有5种专业选择方法,在????大学中有4种专业选择方法.因为没有一个强势专业是两所大学共有的,所以根据分类加法计数原理,这名同学可能的专业选择种数为:????=5+4=9.
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}????大学
????大学
生物学
数学
化学
会计学
医学
信息技术学
物理学
法学
工程学
新知探索
l
l
问题2:如果完成一件事有三类不同方案,在第1类方案中有????1种不同的方法,在第2类方案中有????2种不同的方法,在第3类方案中有????3种不同的方法,那么完成这件事共有多少种不同的方法?
如果完成一件事有????类不同方案,在每一类方案中都有若干种不同的方法,那么应当如何计数呢?
?
l
思考2:用前6个大写英文字母和1~9这9个阿拉伯数字,以????1,????2,…,????9,????1,
????2,…的方式给教室里的一个座位编号,总共能编出多少种不同的号码?
?
新知探索
l
l
这里要完成的事情仍然是“给一个座位编号”,但与前一问题的要求不同.在前一问题中,用26个英文字母中的任意一个或10个阿拉伯数字中的任意一个,都可以给出一个座位号码.但在这个问题中,号码必须由一个英文字母和一个作为下标的阿拉伯数字组成,即得到一个号码要经过先确定一个英文字母,后确定一个阿拉伯数字这样两个步骤.用如图所示的方法可以列出所有可能的号码.
l
新知探索
l
l
也可能这样思考:由于前6个英文字母中的任意一个都能与9个数字中的任意一个组成一个号码,而且它们互不相同,因此共有6×9=54种不同的号码.
?
l
问题3:你能说一说这个问题的特征吗?
上述问题要完成的一件事情仍然是“给一个座位编号”,其中最重要的特征是“和”字的出现:一个座位编号由一个英文字母和一个阿拉伯数字构成.因此得到一个座位号要经过先确定一个英文字母,后确定一个阿拉伯数字这两个步骤,每一个英文字母与不同的数字组成的号码是互不相同的.
新知探索
l
l
l
一般地,有如下分步乘法计数原理:
完成一件事需要两个步骤,做第1步有????种不同的方法,在第2步有????种不同的方法,那么完成这件事共有????=????×????种不同的方法.
?
例析
例2.某班有男生30名、女生24名,从中任选男生和女生各1名代表班级参加比赛,共有多少种不同的选法?
?
l
解:第1步,从30名男生中选出1人,有30种不同选法;第2步,从24名男生中选出1人,有24种不同选法.根据分步乘法计数原理,共有不同选法的种数为????=30×24=720.
?
问题4:如果完成一件事需要三个步骤,做第1步有????1种不同的方法,做第2步有????2种不同的方法,做第3步有????3种不同的方法,那么完成这件事共有多少种不同的方法?
如果完成一件事有????类不同方案,做每一步都有若干种不同的方法,那么应当如何计数呢?
?
例析
例3.书架的第1层放有4本不同的计算机书,第2层放有3本不同的文艺书,第3层放有2本不同的体育书.
(1)从书架上任取1本书,有多少种不同取法?
(2)从书架的第1层、第2层、第3层各取1本书,有多少种不同取法?
l
解:(1)从书架上任取1本书,有三类方案:第1类方案是从第1层取1本计算机书,有4种方法;第2类方案是从第2层取1本文艺书,有3种方法;第3类方案是从第3层取1本体育书,有2种方法.根据分类加法计数原理,不同取法的种数为
????=4+3+2=9.
?
例析
例3.书架的第1层放有4本不同的计算机书,第2层放有3本不同的文艺书,第3层放有2本不同的体育书.
(1)从书架上任取1本书,有多少种不同取法?
(2)从书架的第1层、第2层、第3层各取1本书,有多少种不同取法?
l
解:(2)从书架的第1层、第2层、第3层各取1本书,可以分三个步骤完成:第1步,从第1层取1本计算机书,有4种方法;第2步,从第2层取1本文艺书,有3种方法;第3步,从第3层取1本体育书,有2种方法.根据分步乘法计数原理,不同取法的种数为????=4×3×2=24.
?
新知探索
答案:√,×,×,√.
辨析1.判断正误.
(1)在分类加法计数原理中,每类方案中的方法都能完成这件事.( )
(2)在分类加法计数原理中,两类不同方案中的方法可以相同.( )
(3)在分步乘法计数原理中,事情是分两步完成的,其中任何一个单独的步骤都能完成这件事.( )
(4)在分步乘法计数原理中,每个步骤中完成这个步骤的方法是各不相同的.( )
新知探索
辨析2.从3名女同学和2名男同学中选出一人主持本班一次班会,则不同的选法种数为( ).
A.6 B.5 C.3 D.2
?
答案:B.
辨析3.某商城共有4个门,购物者若从任意一个门进,从任意一个门出,则不同走法的种数是________.
?
答案:16.
练习
题型一:分类加法计数原理
例1.在所有的两位数中,个位数字大于十位数字的两位数的个数为_______.
解:(解法一)根据题意,将十位上的数字按1,2,3,4,5,6,7,8的情况分成8类,在每一类中满足题目条件的两位数分别是8个,7个,6个,5个,4个,3个,2个,1个.根据分类加法计数原理,符合条件的两位数的个数为8+7+6+5+4+3+2+1=36.
?
练习
例1.在所有的两位数中,个位数字大于十位数字的两位数的个数为_______.
解:(解法二)分析个位数字,可分以下几类:
个位是9,则十位可以是1,2,3,?,8中的一个,故共有8个;
个位是8,则十位可以是1,2,3,?,7中的一个,故共有7个;
同理,个位是7的有6个;?个位是2的有1个.
根据分类加法计数原理,符合条件的两位数的个数为8+7+6+5+4+3+2+1=36.
?
练习
方法技巧:
利用分类加法计数原理时的解题流程
(1)分类:将完成这件事的方法分成若干类.
(2)计数:求出每一类的方法数.
(3)结论:将每一类的方法数相加得出结果.
[提醒]确定分类标准时要确保每一类都能独立的完成这件事.
练习
变1.某校高三共有三个班,其各班人数如下表:
(1)从三个班中选一名学生担任学生会主席,有多少种不同的选法?
解(1):从三个班中任选一名学生,可分三类.
第一类,从1班任选一名学生,有50种不同选法;
第二类,从2班任选一名学生,有60种不同选法;
第三类,从3班任选一名学生,有55种不同选法.
根据分类加法计数原理,不同的选法的种数为????=50+60+55=165.
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}班级
男生人数
女生人数
总人数
高三1班
30
20
50
高三2班
30
30
60
高三3班
35
20
55
练习
变1.某校高三共有三个班,其各班人数如下表:
(2)从1班、2班、3班男生中或从3班女生中选一名学生担任学生会生活部部长,有多少种不同的选法?
解(2):由题设知共有三类方案.
第一类,从1班男生中任选一名学生,有30种不同选法;
第二类,从2班男生中任选一名学生,有30种不同选法;
第三类,从3班女生中任选一名学生,有20种不同选法.
根据分类加法计数原理,不同的选法的种数为????=30+30+20=80.
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}班级
男生人数
女生人数
总人数
高三1班
30
20
50
高三2班
30
30
60
高三3班
35
20
55
练习
题型二:分步乘法计数原理
例2.从?2,?1,0,1,2,3这六个数字中任选3个不重复的数字作为二次函数????=????????2+????????+????的系数????,????,????,则可以组成抛物线的条数为多少?
?
解:由题意知????不能为0,故????的值有5种选法;????的值有5种选法;????的值有4种选法.根据分步乘法计数原理,可以组成抛物线的条数为5×5×4=100.
?
练习
方法技巧:
利用分步乘法计数原理时的解题流程
(1)分步:将完成这件事的方法分成若干步.
(2)计数:求出每一步的方法数.
(3)结论:将每一步的方法数相乘得最终结果.
[提醒]分步时要注意不能遗漏步骤,否则就不能完成这件事.
练习
变2.从?2,?1,0,1,2,3这六个数字中任选2个作为椭圆????2????+????2????=1的参数????,????,则可以组成椭圆的个数是多少?
?
解:据条件知????>0,????>0,且????≠????,故需分两步完成,第一步确定????,有3种方法,第二步确定????,有2种方法,根据分步乘法计数原理可以组成椭圆的个数为3×2=6.
?
练习
题型三:两个计数原理的简单综合应用
例3.王华同学有课外参考书若干本,其中有5本不同的外语书,4本不同的数学书,3本不同的物理书,他欲带参考书到图书馆阅读.
(1)若他从这些参考书中带1本去图书馆,有多少种不同的带法?
(2)若带外语、数学、物理参考书各1本,有多少种不同的带法?
解(1):要完成的事情是带1本参考书,无论是带外语书,还是带数学书、物理书,事情都可完成,从而根据分类加法计数原理,不同带法的种数为5+4+3=12.
?
解(2):要完成的事情是带3本不同学科的参考书,只有从外语、数学、物理书中各选1本后,才能完成这件事,因此根据分步乘法计数原理,不同带法的种数为5×4×3=60.
?
练习
方法技巧:
利用两个计数原理解题时的三个注意点
(1)当题目无从下手时,可考虑要完成的这件事是什么,即怎样做才算完成这件事,然后给出完成这件事的一种或几种方法,从这几种方法中归纳出解题方法.
(2)分类时标准要明确,做到不重不漏,有时要恰当画出示意图或树状图,使问题的分析更直观、清楚,便于探索规律.
(3)综合问题一般是先分类再分步.
练习
变3.某电视台的主持人在某综艺节目中拿出两个信箱,其中放着竞猜中成绩优秀的观众来信,甲箱中有30封,乙箱中有20封,现由主持人抽奖确定幸运观众,若先从中确定一名幸运之星,再从两箱中各确定一名幸运观众,则有多少种不同结果?
解:①若幸运之星在甲箱中抽取,
不同结果的种数为30×29×20=17400;
②若幸运之星在乙箱中抽取,
不同结果的种数为20×19×30=11400.
故不同结果的种数为17400+11400=28800.
?
课堂小结
1.分类加法计数原理:
(1)任务:完成一件事;
(2)分类:有两类不同方案,在第1类方案中有????种不同的方法,在第2类方案中有????种不同的方法;
(3)计数:完成这件事共有????=????+????种不同的方法.
[注]????=????1+????2+????3+?+????????.
?
课堂小结
2.分类乘法计数原理:
(1)任务:完成一件事;
(2)分类:需要两个步骤,做第1步有????种不同的方法,做第2步有????种不同的方法;
(3)计数:完成这件事共有????=????×????种不同的方法.
[注]????=????1×????2×????3×?×????????.
?
作业
(1)整理本节课的题型;
(2)课本P5-—P6的练习1——4题;
(3)课本P11习题6.1的第1——6题.
