山东省济宁市微山一中2013-2014学年高二下学期第一次月考数学(文)试题 Word版含答案
文档属性
| 名称 | 山东省济宁市微山一中2013-2014学年高二下学期第一次月考数学(文)试题 Word版含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 169.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-03-29 07:45:07 | ||
图片预览

文档简介
高二下学期第一次月考数学(文)试题
命题人:杨 敏
(满分:150分 时间:120分钟)
注意事项:
1.本试题分第I卷和第Ⅱ卷两部分,第I卷为选择题,共50分;第Ⅱ卷为非选择题,共100分,满分l50分.考试时间为120分钟.
2.答第I卷前,考生务必将姓名、准考证号、考试科目填写清楚,并用2B铅笔涂写在答题卡上,将第I卷选择题的答案涂在答题卡上.
3.答第Ⅱ卷时须将答题纸密封线内的项目填写清楚,第Ⅱ卷的答案用中性笔直接答在答题纸指定的位置上.考试结束后,只收答题卡和第Ⅱ卷答题纸.
第I卷(选择题共50分)
参考公式或数据:
选择题(本大题共10小题,共50分,只有一个答案正确)
1.函数的导数是( )
A. B. C. D.
2.在回归直线方程中,回归系数表示( )
A.当时,的平均值 B.变动一个单位时,的实际变动量
C.变动一个单位时,的平均变动量 D.变动一个单位时,的平均变动量
3.已知对任意实数,有,且时,,则 时( )
A. B.
C. D.
4.下列说法正确的有( )
①回归方程适用于一切样本和总体。②回归方程一般都有时间性。③样本取值的范围会影响回归方程的适用范围。④回归方程得到的预报值是预报变量的精确值。
A. ①② B. ①③ C. ②③ D. ③④
5.曲线在点处的切线与坐标轴所围三角形的面积为( )
A. B. C. D.
6、在两个变量与的回归模型中,分别选择了四个不同的模型,它们的相关指数如下,其中拟合效果最好的为( )
A.模型①的相关指数为 B.模型②的相关指数为
C.模型③的相关指数为 D.模型④的相关指数为
7.若函数在内有极小值,则( )
A. B. C. D.
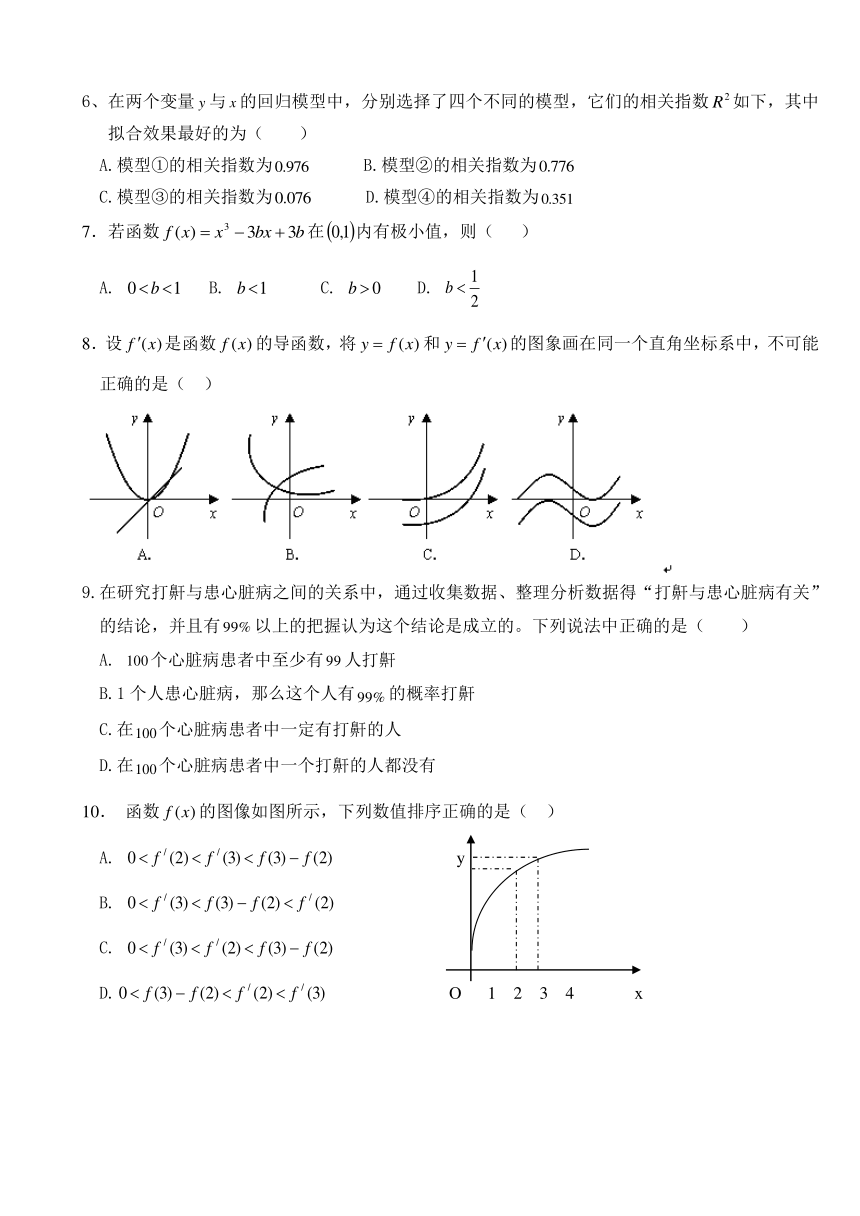
8.设是函数的导函数,将和的图象画在同一个直角坐标系中,不可能正确的是( )
9.在研究打鼾与患心脏病之间的关系中,通过收集数据、整理分析数据得“打鼾与患心脏病有关”的结论,并且有以上的把握认为这个结论是成立的。下列说法中正确的是( )
A. 个心脏病患者中至少有人打鼾
B.1个人患心脏病,那么这个人有的概率打鼾
C.在个心脏病患者中一定有打鼾的人
D.在个心脏病患者中一个打鼾的人都没有
10. 函数的图像如图所示,下列数值排序正确的是( )
A. y
B.
C.
D. O 1 2 3 4 x
第Ⅱ卷(非选择题共100分)
二.填空题(本大题共5小题,共25分)
11.函数的单调递增区间是____.
12.已知函数在区间上的最大值与最小值分别为,则 .
13.已知回归直线方程,其中且样本点中心为,则回归直线方程为
14.已知函数,若函数在总是单调函数,则的取值范围是 .
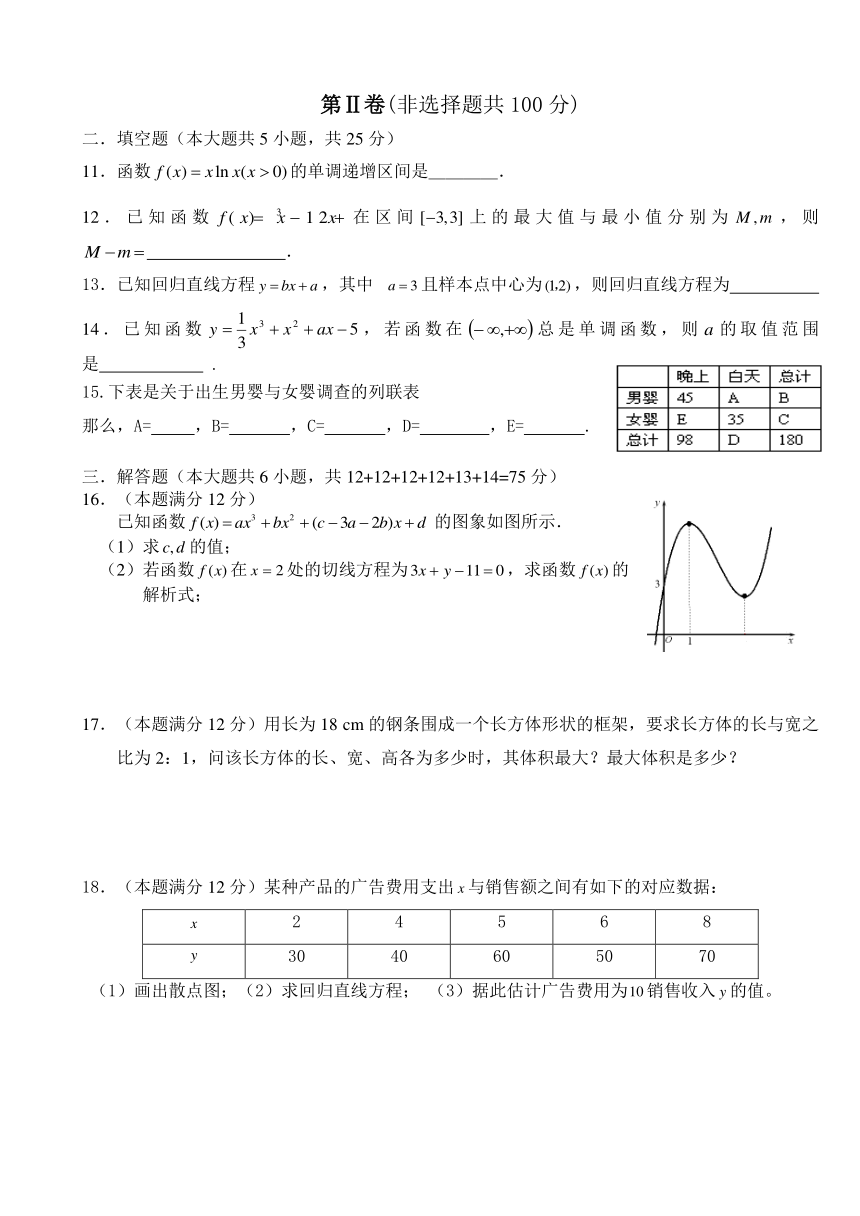
15.下表是关于出生男婴与女婴调查的列联表
那么,A= ,B= ,C= ,D= ,E= .
三.解答题(本大题共6小题,共12+12+12+12+13+14=75分)
16.(本题满分12分)
已知函数的图象如图所示.
(1)求的值;
(2)若函数在处的切线方程为,求函数的
解析式;
17.(本题满分12分)用长为18 cm的钢条围成一个长方体形状的框架,要求长方体的长与宽之比为2:1,问该长方体的长、宽、高各为多少时,其体积最大?最大体积是多少?
18.(本题满分12分)某种产品的广告费用支出与销售额之间有如下的对应数据:
2
4
5
6
8
30
40
60
50
70
(1)画出散点图;(2)求回归直线方程; (3)据此估计广告费用为销售收入的值。
19.(本小题满分12分)
已知是函数的一个极值点().
(1)求实数的值;
(2)求函数在的最大值和最小值.
20.(本题满分13分)在研究色盲与性别的关系调查中,调查了男性500人,其中有50人患色盲,调查的500个女性中10人患色盲,
(1)根据以上的数据建立一个的列联表;
(2)能否在犯错误的概率不超过的前提下,认为“性别与患色盲有关系”?说明你的理由。(注: )
21. (本题满分14分)已知函数
(1)求曲线在点处的切线方程;
(2)若关于的方程有三个不同的实根,求实数的取值范围.
高二年级第二学期第一次阶段检测
数学(文)答案
二、填空题(本大题共5小题,共25分)
11.(开区间也可) 12. 32 13.
14. 15.A=47 B=92 C=88 D=82 E=53
三、解答题(本大题共6小题,共12+12+12+12+13+14=75分)
16解:函数的导函数为 …………(3分)
(I)由图可知 函数的图象过点(0,3),且
得 …………(7分)
(II)依题意 且
解得 所以 …………(12分)
17. 解:设长方体的宽为x(m),则长为2x(m),高为
………(2分)
故长方体的体积为
………(4分)
从而 …………(6分)
令V′(x)=0,解得x=0(舍去)或x=1,因此x=1.
当0<x<1时,V′(x)>0;当1<x<时,V′(x)<0,
故在x=1处V(x)取得极大值,并且这个极大值就是V(x)的最大值。……(10分)
从而最大体积V=V(1)=9×12-6×13=3 (m3),此时长方体的长为2 m,宽为1 m,高为1.5 m.
答:当长方体的长为2 m时,高为1.5 m时,体积最大,最大体积为3 m3。…………(12分)
18.解:(1)图略; …………(4分)
(2),,
,,
,∴,,
∴回归直线方程为。 …………(10分)
(3)时,预报的值为 …………(12分)
19.解:(I)由可得
……(4分)
∵是函数的一个极值点,∴
∴,解得 ……………(6分)
(II)由,得在递增,在递增,
由,得在在递减
∴是在的最小值; ……………(8分)
,
∵
∴在的最大值是. …………(12分)
20.解:(1)
患色盲
不患色盲
总计
男
50
450
500
女
10
490
500
总计
60
940
1000
…………(6分)
(2)假设:“性别与患色盲没有关系”
先算出的观测值:
则有
即是H 成立的概率不超过,
所以,能在犯错误的概率不超过的前提下,认为“性别与患色盲有关系”.
………………………(13分)
命题人:杨 敏
(满分:150分 时间:120分钟)
注意事项:
1.本试题分第I卷和第Ⅱ卷两部分,第I卷为选择题,共50分;第Ⅱ卷为非选择题,共100分,满分l50分.考试时间为120分钟.
2.答第I卷前,考生务必将姓名、准考证号、考试科目填写清楚,并用2B铅笔涂写在答题卡上,将第I卷选择题的答案涂在答题卡上.
3.答第Ⅱ卷时须将答题纸密封线内的项目填写清楚,第Ⅱ卷的答案用中性笔直接答在答题纸指定的位置上.考试结束后,只收答题卡和第Ⅱ卷答题纸.
第I卷(选择题共50分)
参考公式或数据:
选择题(本大题共10小题,共50分,只有一个答案正确)
1.函数的导数是( )
A. B. C. D.
2.在回归直线方程中,回归系数表示( )
A.当时,的平均值 B.变动一个单位时,的实际变动量
C.变动一个单位时,的平均变动量 D.变动一个单位时,的平均变动量
3.已知对任意实数,有,且时,,则 时( )
A. B.
C. D.
4.下列说法正确的有( )
①回归方程适用于一切样本和总体。②回归方程一般都有时间性。③样本取值的范围会影响回归方程的适用范围。④回归方程得到的预报值是预报变量的精确值。
A. ①② B. ①③ C. ②③ D. ③④
5.曲线在点处的切线与坐标轴所围三角形的面积为( )
A. B. C. D.
6、在两个变量与的回归模型中,分别选择了四个不同的模型,它们的相关指数如下,其中拟合效果最好的为( )
A.模型①的相关指数为 B.模型②的相关指数为
C.模型③的相关指数为 D.模型④的相关指数为
7.若函数在内有极小值,则( )
A. B. C. D.
8.设是函数的导函数,将和的图象画在同一个直角坐标系中,不可能正确的是( )
9.在研究打鼾与患心脏病之间的关系中,通过收集数据、整理分析数据得“打鼾与患心脏病有关”的结论,并且有以上的把握认为这个结论是成立的。下列说法中正确的是( )
A. 个心脏病患者中至少有人打鼾
B.1个人患心脏病,那么这个人有的概率打鼾
C.在个心脏病患者中一定有打鼾的人
D.在个心脏病患者中一个打鼾的人都没有
10. 函数的图像如图所示,下列数值排序正确的是( )
A. y
B.
C.
D. O 1 2 3 4 x
第Ⅱ卷(非选择题共100分)
二.填空题(本大题共5小题,共25分)
11.函数的单调递增区间是____.
12.已知函数在区间上的最大值与最小值分别为,则 .
13.已知回归直线方程,其中且样本点中心为,则回归直线方程为
14.已知函数,若函数在总是单调函数,则的取值范围是 .
15.下表是关于出生男婴与女婴调查的列联表
那么,A= ,B= ,C= ,D= ,E= .
三.解答题(本大题共6小题,共12+12+12+12+13+14=75分)
16.(本题满分12分)
已知函数的图象如图所示.
(1)求的值;
(2)若函数在处的切线方程为,求函数的
解析式;
17.(本题满分12分)用长为18 cm的钢条围成一个长方体形状的框架,要求长方体的长与宽之比为2:1,问该长方体的长、宽、高各为多少时,其体积最大?最大体积是多少?
18.(本题满分12分)某种产品的广告费用支出与销售额之间有如下的对应数据:
2
4
5
6
8
30
40
60
50
70
(1)画出散点图;(2)求回归直线方程; (3)据此估计广告费用为销售收入的值。
19.(本小题满分12分)
已知是函数的一个极值点().
(1)求实数的值;
(2)求函数在的最大值和最小值.
20.(本题满分13分)在研究色盲与性别的关系调查中,调查了男性500人,其中有50人患色盲,调查的500个女性中10人患色盲,
(1)根据以上的数据建立一个的列联表;
(2)能否在犯错误的概率不超过的前提下,认为“性别与患色盲有关系”?说明你的理由。(注: )
21. (本题满分14分)已知函数
(1)求曲线在点处的切线方程;
(2)若关于的方程有三个不同的实根,求实数的取值范围.
高二年级第二学期第一次阶段检测
数学(文)答案
二、填空题(本大题共5小题,共25分)
11.(开区间也可) 12. 32 13.
14. 15.A=47 B=92 C=88 D=82 E=53
三、解答题(本大题共6小题,共12+12+12+12+13+14=75分)
16解:函数的导函数为 …………(3分)
(I)由图可知 函数的图象过点(0,3),且
得 …………(7分)
(II)依题意 且
解得 所以 …………(12分)
17. 解:设长方体的宽为x(m),则长为2x(m),高为
………(2分)
故长方体的体积为
………(4分)
从而 …………(6分)
令V′(x)=0,解得x=0(舍去)或x=1,因此x=1.
当0<x<1时,V′(x)>0;当1<x<时,V′(x)<0,
故在x=1处V(x)取得极大值,并且这个极大值就是V(x)的最大值。……(10分)
从而最大体积V=V(1)=9×12-6×13=3 (m3),此时长方体的长为2 m,宽为1 m,高为1.5 m.
答:当长方体的长为2 m时,高为1.5 m时,体积最大,最大体积为3 m3。…………(12分)
18.解:(1)图略; …………(4分)
(2),,
,,
,∴,,
∴回归直线方程为。 …………(10分)
(3)时,预报的值为 …………(12分)
19.解:(I)由可得
……(4分)
∵是函数的一个极值点,∴
∴,解得 ……………(6分)
(II)由,得在递增,在递增,
由,得在在递减
∴是在的最小值; ……………(8分)
,
∵
∴在的最大值是. …………(12分)
20.解:(1)
患色盲
不患色盲
总计
男
50
450
500
女
10
490
500
总计
60
940
1000
…………(6分)
(2)假设:“性别与患色盲没有关系”
先算出的观测值:
则有
即是H 成立的概率不超过,
所以,能在犯错误的概率不超过的前提下,认为“性别与患色盲有关系”.
………………………(13分)
同课章节目录
