山东省济宁市微山一中2013-2014学年高二下学期第一次月考数学(理)试题 Word版含答案
文档属性
| 名称 | 山东省济宁市微山一中2013-2014学年高二下学期第一次月考数学(理)试题 Word版含答案 |

|
|
| 格式 | zip | ||
| 文件大小 | 375.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-03-29 00:00:00 | ||
图片预览



文档简介
高二下学期第一次月考数学(理)试题
命题人:罗红孝
注意事项:
1.本试题分第I卷和第Ⅱ卷两部分,第I卷为选择题, 50分;第Ⅱ卷为非选择题,共100分,满分l50分.考试时间为120分钟.
2.答第I卷前,考生务必将姓名、准考证号、考试科目填写清楚,并用2B铅笔涂写在答题卡上,将第I卷选择题的答案涂在答题卡上.
3.答第Ⅱ卷时须将答题纸密封线内的项目填写清楚,第Ⅱ卷的答案用中性笔直接答在答题纸指定的位置上.考试结束后,只收答题卡和第Ⅱ卷答题纸.
第I卷(选择题共50分)
一、选择题:本大题共l0小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.在曲线上切线的倾斜角为的点是( )
A.(0,0) B.(2,4) C. D.
2. 若直线的方向向量为,平面的法向量为,则能使的是( )
A. B.
C. D.
3. 设,则此函数在区间(0,1)内为( )
A.单调递增 B. 有增有减 C.单调递减 D.不确定
4. 已知三点不共线,点为平面外的一点,则下列条件中,
能得到平面的充分条件是( )
A. ; B. ;
C. ; D.
5. 等于
A.1 B. C. D.
6. 正方体-棱长为1,E是中点,则E到平面的距离是
A. B. C. D.
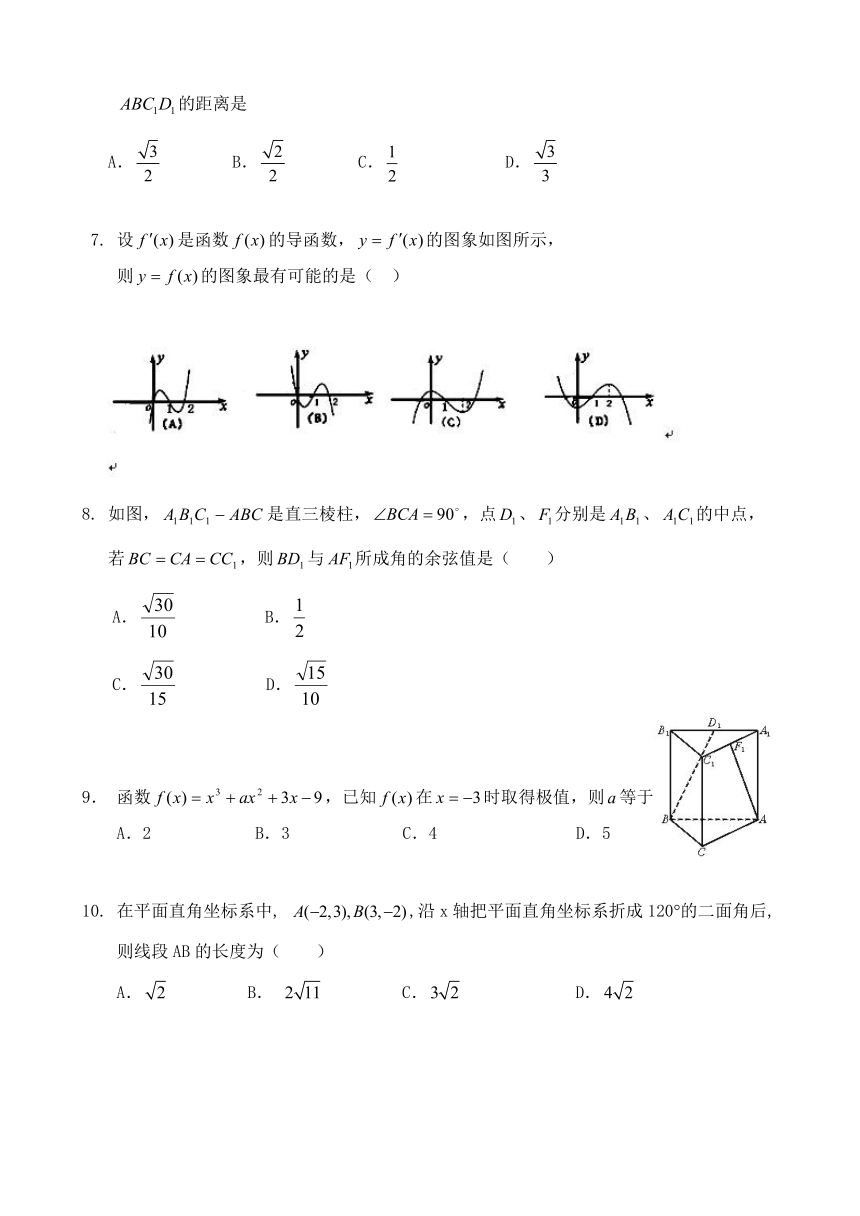
7. 设是函数的导函数,的图象如图所示,
则的图象最有可能的是( )
8. 如图,是直三棱柱,,点、分别是、的中点,
若,则与所成角的余弦值是( )
A. B.
C. D.
9. 函数,已知在时取得极值,则等于( )
A.2 B.3 C.4 D.5
10. 在平面直角坐标系中, ,沿x轴把平面直角坐标系折成120(的二面角后,
则线段AB的长度为( )
A. B. C. D.
第Ⅱ卷(非选择题共100分)
二、填空题:本大题共5小题,每小题5分,共25分.
11.设.若曲线与直线,所围成封闭图形的面积为,则=__ ____.
12.如图,在正方体中,、分别是、的 中点,
则异面直线与所成角的大小是____________.
13.函数在区间上的最大值是 .
14.设函数,若关于的方程有三个不同实根,
则的取值范围是______________ .
15.给出下列命题
①已知,则;
②为空间四点,若不构成空间的一个基底,则共面;
③已知,则与任何向量不构成空间的一个基底;
④已知是空间的一个基底,则基向量可以与向量构成空间另一个基底.
其中所有正确命题的序号为______________.
三、解答题:本大题共6小题,共75分,解答应写出文字说明,证明过程或演算步骤.
16.(本小题满分12分)
设函数 的图象与直线相切于.
(Ⅰ)求, 的值;
(Ⅱ)讨论函数的单调性.
17.(本小题满分12分)
已知三棱锥中,平面,AB⊥AC,,
N为AB上一点,,分别为PB,BC的中点.
(Ⅰ)证明:;
(Ⅱ)求与平面所成角的大小.
18(本小题满分12分)
设的导数满足,其中常数.
(Ⅰ)求曲线在点处的切线方程;
(Ⅱ) 设,求函数的极值.
19.(本小题满分12分)
如图,已知正三棱柱的侧棱长和底面边长均为1,
是底面边上的中点,是侧棱上的点,且
(Ⅰ)求二面角的平面角的余弦值;
(Ⅱ)求点到平面的距离。
20(本小题满分13分)
某商场销售某种商品的经验表明,该商品每日的销售量(单位:千克)与销售价格(单位:元/千克)满足关系式=,其中3<<6,为常数,已知销售价格为5元/千克时,每日可售出该商品11千克。
(I) 求的值
(Ⅱ)若该商品的成本为3元/千克,试确定销售价格的值,使商场每日销售该商品所获得的利润最大。
21.(本小题满分14分)
如图所示,在底面是菱形的四棱锥中,
,,点在上,且.
(Ⅰ)证明:平面;
(Ⅱ)求二面角的大小;
(Ⅲ)棱上是否存在一点,使平面?证明你的结论。
2012级高二年级下学期阶段测试
数学试题(理)参考答案 (2014.3)
三、解答题: 16(本小题满分12分)
解:(Ⅰ)求导得
由于的图象与直线相切于点(1,-11)
所以,即 解得 .(6分)
(Ⅱ)由得
令,解得;又令,解得
所以当时,是增函数;当时,也是增函数;
但时,是减函数. (12分)
17. (本题满分12分)
18.(本小题满分12分)
解:(I)因故
令
由已知
又令由已知
因此解得
因此
又因为故曲线处的切线方程为
(6分)
(II)由(I)知,从而有
令
当上为减函数;
当在(0,3)上为增函数;
当时,上为减函数;
从而函数处取得极小值处取得极大值(12分)
19.(本小题满分12分)
解:(Ⅰ)建立如图所示的空间直角坐标系,则(0,0,1),M(0,,0),C(0,1,0), N (0,1,) , A (),所以,
,,。
因为所以,同法可得。故﹤﹥为二面角—AM—N的平面角
∴﹤﹥=
故所求二面角—AM—N的平面角的余弦值为。(6分)
(Ⅱ)设n=(x,y,z)为平面AMN的一个法向量,则由得
故可取
设与n的夹角为a,则。
所以到平面AMN的距离为。(12分)
20(本小题满分13分)
解:(I)∵当=5时,=11,∴=11,解得=2;(4分)
(II)由(I)知该商品每日的销售量=(3<<6),
∴该商城每日的销售该商品的利润
==(3<<6),(7分)
∴==(9分)
当变化时,,的变化情况如下表:
(3,4)
4
(4,6)
+
0
-
单调递增
极大值42
单调递减
由上表可得,=4是函数在区间(3,6)内的极大值点,也是最大值点,
∴当=4时,=42. (13分)
答:当销售价格定为4元/千克时,商场每日销售该商品所获得的利润最大.
由,得
∴
∴由图可知二面角E-AC-D的大小为.(10分)
命题人:罗红孝
注意事项:
1.本试题分第I卷和第Ⅱ卷两部分,第I卷为选择题, 50分;第Ⅱ卷为非选择题,共100分,满分l50分.考试时间为120分钟.
2.答第I卷前,考生务必将姓名、准考证号、考试科目填写清楚,并用2B铅笔涂写在答题卡上,将第I卷选择题的答案涂在答题卡上.
3.答第Ⅱ卷时须将答题纸密封线内的项目填写清楚,第Ⅱ卷的答案用中性笔直接答在答题纸指定的位置上.考试结束后,只收答题卡和第Ⅱ卷答题纸.
第I卷(选择题共50分)
一、选择题:本大题共l0小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.在曲线上切线的倾斜角为的点是( )
A.(0,0) B.(2,4) C. D.
2. 若直线的方向向量为,平面的法向量为,则能使的是( )
A. B.
C. D.
3. 设,则此函数在区间(0,1)内为( )
A.单调递增 B. 有增有减 C.单调递减 D.不确定
4. 已知三点不共线,点为平面外的一点,则下列条件中,
能得到平面的充分条件是( )
A. ; B. ;
C. ; D.
5. 等于
A.1 B. C. D.
6. 正方体-棱长为1,E是中点,则E到平面的距离是
A. B. C. D.
7. 设是函数的导函数,的图象如图所示,
则的图象最有可能的是( )
8. 如图,是直三棱柱,,点、分别是、的中点,
若,则与所成角的余弦值是( )
A. B.
C. D.
9. 函数,已知在时取得极值,则等于( )
A.2 B.3 C.4 D.5
10. 在平面直角坐标系中, ,沿x轴把平面直角坐标系折成120(的二面角后,
则线段AB的长度为( )
A. B. C. D.
第Ⅱ卷(非选择题共100分)
二、填空题:本大题共5小题,每小题5分,共25分.
11.设.若曲线与直线,所围成封闭图形的面积为,则=__ ____.
12.如图,在正方体中,、分别是、的 中点,
则异面直线与所成角的大小是____________.
13.函数在区间上的最大值是 .
14.设函数,若关于的方程有三个不同实根,
则的取值范围是______________ .
15.给出下列命题
①已知,则;
②为空间四点,若不构成空间的一个基底,则共面;
③已知,则与任何向量不构成空间的一个基底;
④已知是空间的一个基底,则基向量可以与向量构成空间另一个基底.
其中所有正确命题的序号为______________.
三、解答题:本大题共6小题,共75分,解答应写出文字说明,证明过程或演算步骤.
16.(本小题满分12分)
设函数 的图象与直线相切于.
(Ⅰ)求, 的值;
(Ⅱ)讨论函数的单调性.
17.(本小题满分12分)
已知三棱锥中,平面,AB⊥AC,,
N为AB上一点,,分别为PB,BC的中点.
(Ⅰ)证明:;
(Ⅱ)求与平面所成角的大小.
18(本小题满分12分)
设的导数满足,其中常数.
(Ⅰ)求曲线在点处的切线方程;
(Ⅱ) 设,求函数的极值.
19.(本小题满分12分)
如图,已知正三棱柱的侧棱长和底面边长均为1,
是底面边上的中点,是侧棱上的点,且
(Ⅰ)求二面角的平面角的余弦值;
(Ⅱ)求点到平面的距离。
20(本小题满分13分)
某商场销售某种商品的经验表明,该商品每日的销售量(单位:千克)与销售价格(单位:元/千克)满足关系式=,其中3<<6,为常数,已知销售价格为5元/千克时,每日可售出该商品11千克。
(I) 求的值
(Ⅱ)若该商品的成本为3元/千克,试确定销售价格的值,使商场每日销售该商品所获得的利润最大。
21.(本小题满分14分)
如图所示,在底面是菱形的四棱锥中,
,,点在上,且.
(Ⅰ)证明:平面;
(Ⅱ)求二面角的大小;
(Ⅲ)棱上是否存在一点,使平面?证明你的结论。
2012级高二年级下学期阶段测试
数学试题(理)参考答案 (2014.3)
三、解答题: 16(本小题满分12分)
解:(Ⅰ)求导得
由于的图象与直线相切于点(1,-11)
所以,即 解得 .(6分)
(Ⅱ)由得
令,解得;又令,解得
所以当时,是增函数;当时,也是增函数;
但时,是减函数. (12分)
17. (本题满分12分)
18.(本小题满分12分)
解:(I)因故
令
由已知
又令由已知
因此解得
因此
又因为故曲线处的切线方程为
(6分)
(II)由(I)知,从而有
令
当上为减函数;
当在(0,3)上为增函数;
当时,上为减函数;
从而函数处取得极小值处取得极大值(12分)
19.(本小题满分12分)
解:(Ⅰ)建立如图所示的空间直角坐标系,则(0,0,1),M(0,,0),C(0,1,0), N (0,1,) , A (),所以,
,,。
因为所以,同法可得。故﹤﹥为二面角—AM—N的平面角
∴﹤﹥=
故所求二面角—AM—N的平面角的余弦值为。(6分)
(Ⅱ)设n=(x,y,z)为平面AMN的一个法向量,则由得
故可取
设与n的夹角为a,则。
所以到平面AMN的距离为。(12分)
20(本小题满分13分)
解:(I)∵当=5时,=11,∴=11,解得=2;(4分)
(II)由(I)知该商品每日的销售量=(3<<6),
∴该商城每日的销售该商品的利润
==(3<<6),(7分)
∴==(9分)
当变化时,,的变化情况如下表:
(3,4)
4
(4,6)
+
0
-
单调递增
极大值42
单调递减
由上表可得,=4是函数在区间(3,6)内的极大值点,也是最大值点,
∴当=4时,=42. (13分)
答:当销售价格定为4元/千克时,商场每日销售该商品所获得的利润最大.
由,得
∴
∴由图可知二面角E-AC-D的大小为.(10分)
同课章节目录
