沪科版七年级下册数学 10.1.2垂线及其性质、画法 教案
文档属性
| 名称 | 沪科版七年级下册数学 10.1.2垂线及其性质、画法 教案 |

|
|
| 格式 | doc | ||
| 文件大小 | 153.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-22 17:14:21 | ||
图片预览


文档简介
垂线及其性质
一、教材分析
地位和作用 垂直是平面内两条直线相交的一种特殊情形,在学生已有知识和经验的基础上来进一步研究平面内两条直线垂直的情形。在本节课中,首先探究两直线垂直的定义及过一点画已知直线的垂线的方法,后面经过观察、动手画、折纸等得出了垂线的性质定理1:过一点有且只有一条直线与已知直线垂直。本节课应在解决问题的过程中,注意学生推理能力的培养,引导学生观察,分析,猜想,得出结论。
2、学情分析 学生在上节课已经学习了相交线,复习旧知时引出当两直线相交其中一个角是90度时,就是垂直,学生以前也接触过这种从一般到特殊的情形。课堂中可以利用多媒体,动画等充分调动学生学习的积极性,引导学生积极开展思维活动,主动探索,获取新知,从具体事物到抽象理论,这符合学生的心理特征和认知规律。
教学目标知识与技能:1、理解并掌握垂线的定义及画法。 2、理解垂线的基本性质1并会运用其解决问题。过程与方法:经历观察、操作、交流等活动,进一步发展 空间观念,培养学生推理能力和表达能力。情感态度与价值观:发展学生在数学活动中的探究意识和合作交流的习惯,体会垂线性质定理的应用,培养学生勤于动手,乐于思考的品质。
4、教学重难点:重点:垂线及垂线基本性质1的理解与应用。难点:垂线性质的推理过程及应用。
学法分析学生在学习垂线及其性质定理1时,应按照探索垂线性质定理1,再验证垂线性质定理1,最后再应用垂线性质定理1的思路进行学习。本节课学法指导的重点是:观察、分析、概括、归纳、验证,鼓励学生要善于动手,通过动手来实现问题的转化。
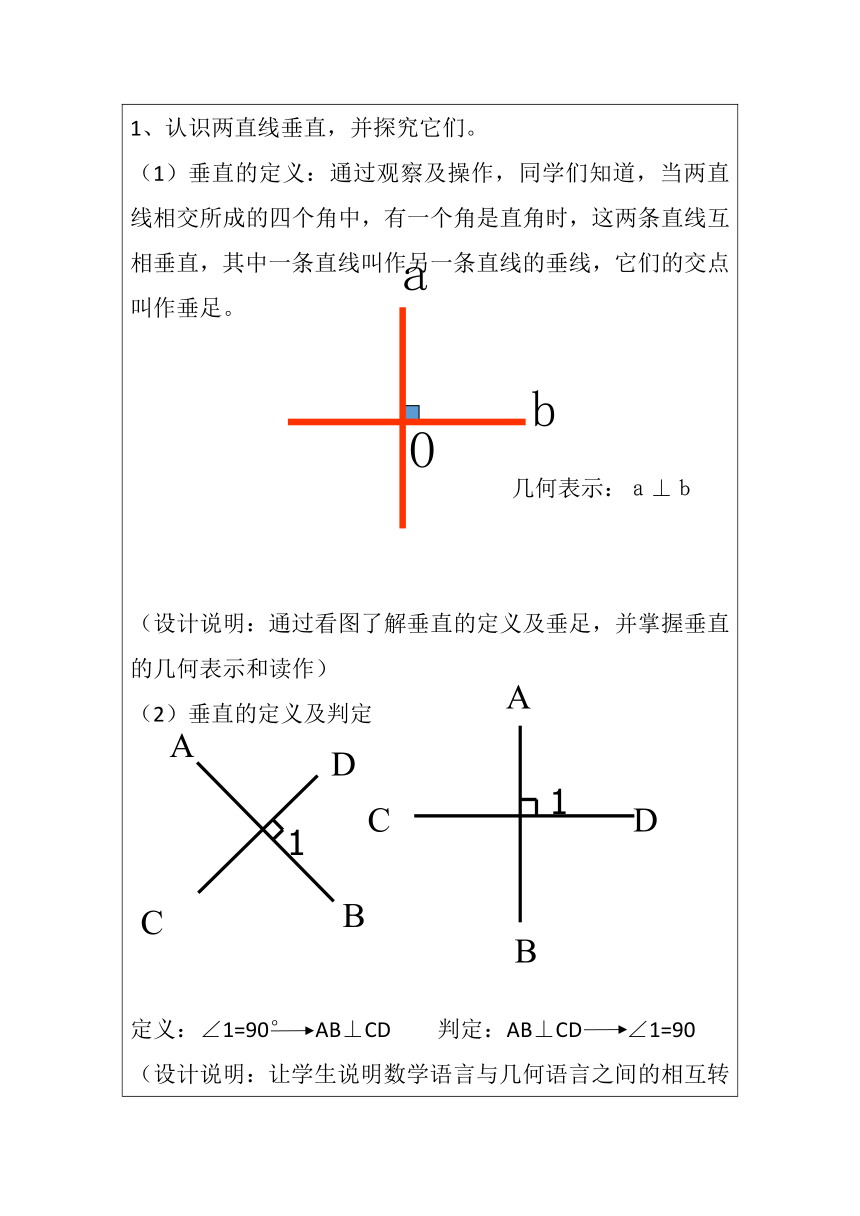
教学过程复习旧知,引入新知引导学生观看模型及图片,复习上节课学习的两直线相交中的对顶角及邻补角,当直线AB不动,CD绕AB转动,∠1 =∠2时, ∠1 ,∠2 ,∠3的度数各为多少?从而引出两直线垂直是两直线相交的一种特殊情形。(设计说明:通过学生上节课学习的相交线,对顶角相等及邻补角互补,得出两直线垂直,也让学生明白了前后知识的联系。) 探究新知,解决问题认识两直线垂直,并探究它们。垂直的定义:通过观察及操作,同学们知道,当两直线相交所成的四个角中,有一个角是直角时,这两条直线互相垂直,其中一条直线叫作另一条直线的垂线,它们的交点叫作垂足。 几何表示:a⊥b (设计说明:通过看图了解垂直的定义及垂足,并掌握垂直的几何表示和读作)垂直的定义及判定 定义:∠1=90° AB⊥CD 判定:AB⊥CD ∠1=90(设计说明:让学生说明数学语言与几何语言之间的相互转化,为以后的几何说理做准备。)场所语言:生活中有许多垂直的例子,你能举出一些例子吗?学生举例,并观察图片。(设计说明:通过生活中的实例,让学生了解两直线垂直是我们生活中经常见到的,有用的,通过图片,培养学生的空间想象力,启发学生广泛联想。)
探究垂线的画法问题::如何过一点画已知直线的垂线呢?(学生观察图片中画垂线的一种情况并总结,另一种情况学生自己动手画,教师演示并总结。)老师演示用折纸法,过一点找出已知直线的垂线,另一种情况让学生自己动手操作。(设计说明:让学生先观察再动手画,动手折叠,再小组交流分类讨论、总结得出垂线性质定理1,从而充分调动学生的积极性。(4)教师总结垂线的性质,让学生在此名确。
小试牛刀1、如图,(1)过点A作BC的垂线 (2)过点B作AC的垂线。2、如图:直线AB与直线CD相交于点O,OE⊥AB,已知∠BOD=45°,求∠COE的度数3、如图,直线AB、CD相交于点O,OE⊥CD,∠AOC=40°,求∠DOB和∠BOE的度数. (设计说明:通过练习加强学生对知识的理解,训练学生对垂直的语言表达,进一步巩固学生对垂直的理解,培养学生灵活运用知识解决问题的能力。)
反思总结、情谊发展今天数学课学习的内容是《10.1.2垂直》学生通过对垂直的探究,我发现生活中有很多垂直现象,数学来源于生活又运用于生活。我们还得出了垂线的画法有三步:一靠,二推,三画,接着通过画图、折纸等操作,运用了分类讨论的数学思想得出了垂线的性质是:过一点有且只有一条直线垂直于已知直线。但是,我对画钝角三角形的垂线仍有疑惑,仍需继续努力。
布置作业课本121页第1、2题
板书设计一、垂直定义: 几何语言:因为∠1=90° 所以AB⊥CD 垂线的性质1:(分类讨论) 应用
b
a
O
A
B
C
D
1
A
B
C
D
1
E
C
A
D
B
一、教材分析
地位和作用 垂直是平面内两条直线相交的一种特殊情形,在学生已有知识和经验的基础上来进一步研究平面内两条直线垂直的情形。在本节课中,首先探究两直线垂直的定义及过一点画已知直线的垂线的方法,后面经过观察、动手画、折纸等得出了垂线的性质定理1:过一点有且只有一条直线与已知直线垂直。本节课应在解决问题的过程中,注意学生推理能力的培养,引导学生观察,分析,猜想,得出结论。
2、学情分析 学生在上节课已经学习了相交线,复习旧知时引出当两直线相交其中一个角是90度时,就是垂直,学生以前也接触过这种从一般到特殊的情形。课堂中可以利用多媒体,动画等充分调动学生学习的积极性,引导学生积极开展思维活动,主动探索,获取新知,从具体事物到抽象理论,这符合学生的心理特征和认知规律。
教学目标知识与技能:1、理解并掌握垂线的定义及画法。 2、理解垂线的基本性质1并会运用其解决问题。过程与方法:经历观察、操作、交流等活动,进一步发展 空间观念,培养学生推理能力和表达能力。情感态度与价值观:发展学生在数学活动中的探究意识和合作交流的习惯,体会垂线性质定理的应用,培养学生勤于动手,乐于思考的品质。
4、教学重难点:重点:垂线及垂线基本性质1的理解与应用。难点:垂线性质的推理过程及应用。
学法分析学生在学习垂线及其性质定理1时,应按照探索垂线性质定理1,再验证垂线性质定理1,最后再应用垂线性质定理1的思路进行学习。本节课学法指导的重点是:观察、分析、概括、归纳、验证,鼓励学生要善于动手,通过动手来实现问题的转化。
教学过程复习旧知,引入新知引导学生观看模型及图片,复习上节课学习的两直线相交中的对顶角及邻补角,当直线AB不动,CD绕AB转动,∠1 =∠2时, ∠1 ,∠2 ,∠3的度数各为多少?从而引出两直线垂直是两直线相交的一种特殊情形。(设计说明:通过学生上节课学习的相交线,对顶角相等及邻补角互补,得出两直线垂直,也让学生明白了前后知识的联系。) 探究新知,解决问题认识两直线垂直,并探究它们。垂直的定义:通过观察及操作,同学们知道,当两直线相交所成的四个角中,有一个角是直角时,这两条直线互相垂直,其中一条直线叫作另一条直线的垂线,它们的交点叫作垂足。 几何表示:a⊥b (设计说明:通过看图了解垂直的定义及垂足,并掌握垂直的几何表示和读作)垂直的定义及判定 定义:∠1=90° AB⊥CD 判定:AB⊥CD ∠1=90(设计说明:让学生说明数学语言与几何语言之间的相互转化,为以后的几何说理做准备。)场所语言:生活中有许多垂直的例子,你能举出一些例子吗?学生举例,并观察图片。(设计说明:通过生活中的实例,让学生了解两直线垂直是我们生活中经常见到的,有用的,通过图片,培养学生的空间想象力,启发学生广泛联想。)
探究垂线的画法问题::如何过一点画已知直线的垂线呢?(学生观察图片中画垂线的一种情况并总结,另一种情况学生自己动手画,教师演示并总结。)老师演示用折纸法,过一点找出已知直线的垂线,另一种情况让学生自己动手操作。(设计说明:让学生先观察再动手画,动手折叠,再小组交流分类讨论、总结得出垂线性质定理1,从而充分调动学生的积极性。(4)教师总结垂线的性质,让学生在此名确。
小试牛刀1、如图,(1)过点A作BC的垂线 (2)过点B作AC的垂线。2、如图:直线AB与直线CD相交于点O,OE⊥AB,已知∠BOD=45°,求∠COE的度数3、如图,直线AB、CD相交于点O,OE⊥CD,∠AOC=40°,求∠DOB和∠BOE的度数. (设计说明:通过练习加强学生对知识的理解,训练学生对垂直的语言表达,进一步巩固学生对垂直的理解,培养学生灵活运用知识解决问题的能力。)
反思总结、情谊发展今天数学课学习的内容是《10.1.2垂直》学生通过对垂直的探究,我发现生活中有很多垂直现象,数学来源于生活又运用于生活。我们还得出了垂线的画法有三步:一靠,二推,三画,接着通过画图、折纸等操作,运用了分类讨论的数学思想得出了垂线的性质是:过一点有且只有一条直线垂直于已知直线。但是,我对画钝角三角形的垂线仍有疑惑,仍需继续努力。
布置作业课本121页第1、2题
板书设计一、垂直定义: 几何语言:因为∠1=90° 所以AB⊥CD 垂线的性质1:(分类讨论) 应用
b
a
O
A
B
C
D
1
A
B
C
D
1
E
C
A
D
B
