沪科版八下17.4《一元二次方程根与系数的关系》ppt课件
文档属性
| 名称 | 沪科版八下17.4《一元二次方程根与系数的关系》ppt课件 |  | |
| 格式 | zip | ||
| 文件大小 | 862.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-03-29 15:33:40 | ||
图片预览


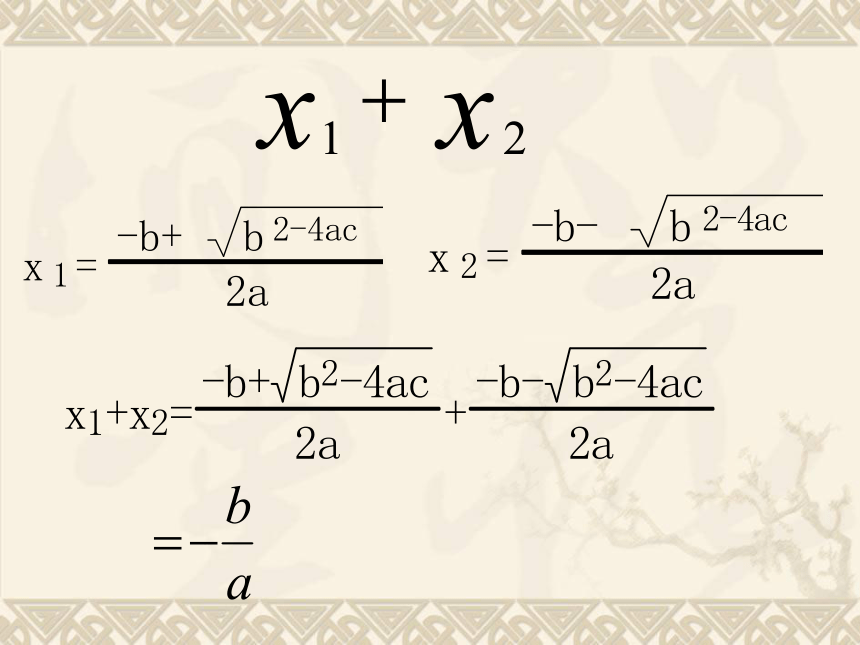
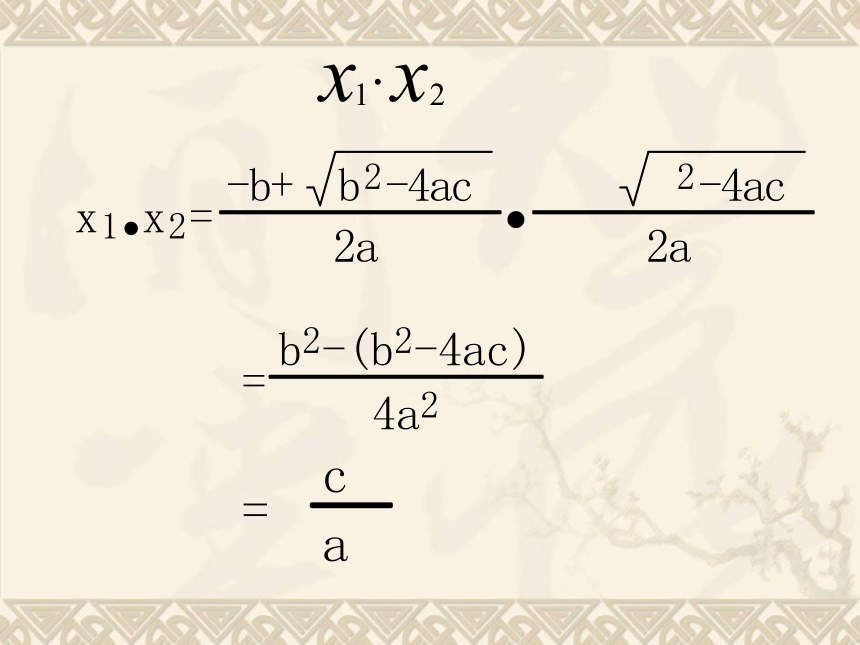



文档简介
课件20张PPT。 17.4一元二次方程
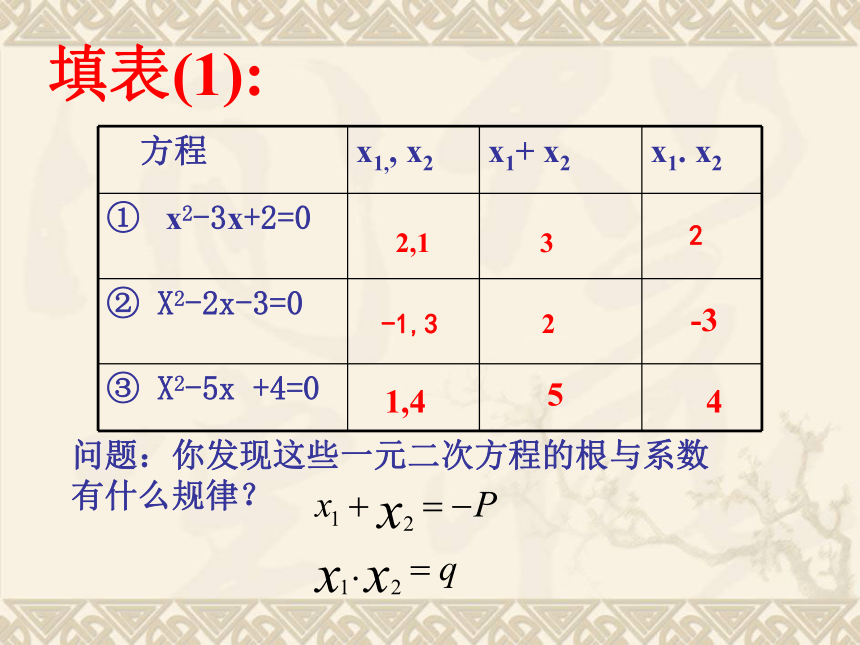
——根与系数关系 问题:你发现这些一元二次方程的根与系数
有什么规律?
2,13
2
-1,32-31,4
5
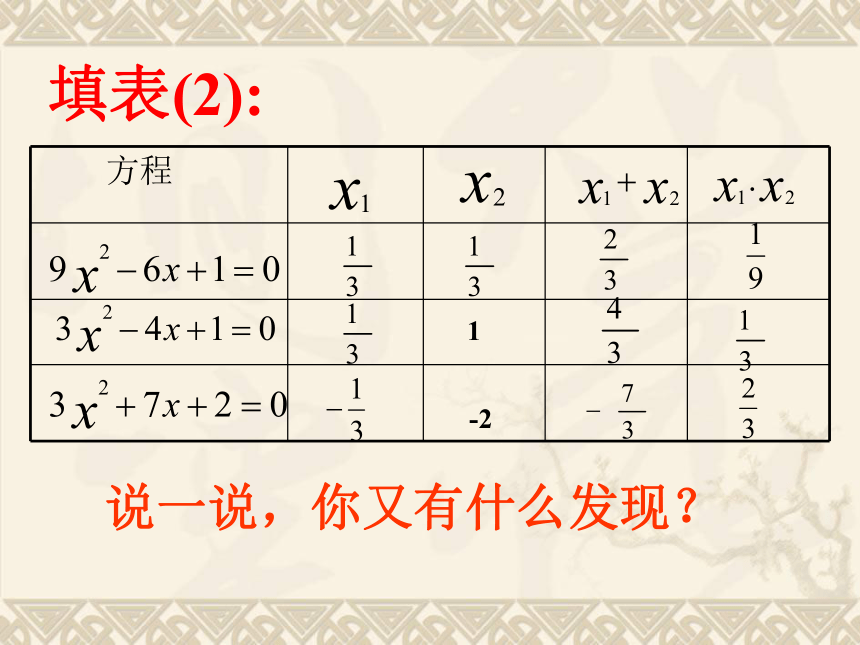
4填表(1):1-2填表(2):说一说,你又有什么发现? 如果关于x的一元二次方程的两根是 , ,则: 如果关于x的一元二次方程的两根是 , ,则:一元二次方程根与系数的关系是法国数学家“韦达”发现的,所以我们又称之为韦达定理.411412例1:则:==应用一:求值例2、已知方程X2+kX+k+2=0的两个根是X1、
X2,且X12+X22 = 4,求k的值。 解:由根与系数的关系得:
X1+X2=-k, X1?X2=k+2
又X12+ X2 2 = 4
即(X1+ X2)2 - 2 X1X2=4
∴K2- 2(k+2)=4
∴K2-2k-8=0
解得:k=4 或k=-2∵ △= K2-4(k+2)
当k=4时, △<0
当k=-2时,△>0
∴ k=-2另外几种常见的求值以 为两根的一元二次方程
(二次项系数为1)为:应用二:已知两根求作新的方程例3: 以方程X2+3X-5=0的两个根的相反数为根的方程是( )
A、y2+3y-5=0 B、 y2-3y-5=0
C、y2+3y+5=0 D、 y2-3y+5=0B解:设原方程两根为 则:新方程的两根之和为新方程的两根之积为例4: 已知两个数的和是1,积是-2,则两 个数是 。2和-1解法(一):设两数分别为x,y则:{解得:x=2
y=-1{或 x=-1
y=2{解法(二):设两数分别为一个一元二次方程
的两根则:求得∴两数为2,-1应用三:已知两个数的和与积,求两数 例5. 已知方程 2x2+kx-4=0的一个根是-4,求它的另一个根及k的值。解:设方程的另一根为了 ,则应用四:求方程中的待定系数例6、利用根与系数的关系,求一元二次方程
两个根的;(1)平方和;(2)倒数和解:设方程的两个根是x1 x2,那么例7: 已知方程x2-5x-2=0,作一个新方程,
使它的根分别是已知方程各根平方的倒数解:设x1、x2为方程x2-5x-2=0的两根,则
x1+x2=5 x1x2=-2设所求方程两根为y1、y2则:
例8.已知方程x2+2(m-2)x+m2+4=0有两个实数根,且这两个根的平方和比两根的积大21,求m的值.
解:设x1、x2为方程的两根∵方程有两个实数根,
解得m≤0.
依题意,得
∵m≤0,
∴m=-1.
(x12+x22)-x1x2=21 例9. 试确定m的值,使关于x的方程8x2-(2m2+m-6)x+2m-1=0的两根互为相反数.
解:设此方程的两个根为x1、x2,要使方程的两个根互为相反数,必需满足条件:
Δ
x1+x2=0,
x1x2≤0.
0,
得2m2+m-6=0
∴当m=-2时,原方程的两根互为相反数.
例10 方程
有一个正根,一个负根,求m的取值范围。解:由已知,△={即{m>0
m-1<0∴0X1X2<0两个正根△≥0
X1X2>0
X1+X2>0两个负根△≥0
X1X2>0
X1+X2<0{{{ 一元二次方程 ax2+bx+c=0(a≠0)的两个根
——根与系数关系 问题:你发现这些一元二次方程的根与系数
有什么规律?
2,13
2
-1,32-31,4
5
4填表(1):1-2填表(2):说一说,你又有什么发现? 如果关于x的一元二次方程的两根是 , ,则: 如果关于x的一元二次方程的两根是 , ,则:一元二次方程根与系数的关系是法国数学家“韦达”发现的,所以我们又称之为韦达定理.411412例1:则:==应用一:求值例2、已知方程X2+kX+k+2=0的两个根是X1、
X2,且X12+X22 = 4,求k的值。 解:由根与系数的关系得:
X1+X2=-k, X1?X2=k+2
又X12+ X2 2 = 4
即(X1+ X2)2 - 2 X1X2=4
∴K2- 2(k+2)=4
∴K2-2k-8=0
解得:k=4 或k=-2∵ △= K2-4(k+2)
当k=4时, △<0
当k=-2时,△>0
∴ k=-2另外几种常见的求值以 为两根的一元二次方程
(二次项系数为1)为:应用二:已知两根求作新的方程例3: 以方程X2+3X-5=0的两个根的相反数为根的方程是( )
A、y2+3y-5=0 B、 y2-3y-5=0
C、y2+3y+5=0 D、 y2-3y+5=0B解:设原方程两根为 则:新方程的两根之和为新方程的两根之积为例4: 已知两个数的和是1,积是-2,则两 个数是 。2和-1解法(一):设两数分别为x,y则:{解得:x=2
y=-1{或 x=-1
y=2{解法(二):设两数分别为一个一元二次方程
的两根则:求得∴两数为2,-1应用三:已知两个数的和与积,求两数 例5. 已知方程 2x2+kx-4=0的一个根是-4,求它的另一个根及k的值。解:设方程的另一根为了 ,则应用四:求方程中的待定系数例6、利用根与系数的关系,求一元二次方程
两个根的;(1)平方和;(2)倒数和解:设方程的两个根是x1 x2,那么例7: 已知方程x2-5x-2=0,作一个新方程,
使它的根分别是已知方程各根平方的倒数解:设x1、x2为方程x2-5x-2=0的两根,则
x1+x2=5 x1x2=-2设所求方程两根为y1、y2则:
例8.已知方程x2+2(m-2)x+m2+4=0有两个实数根,且这两个根的平方和比两根的积大21,求m的值.
解:设x1、x2为方程的两根∵方程有两个实数根,
解得m≤0.
依题意,得
∵m≤0,
∴m=-1.
(x12+x22)-x1x2=21 例9. 试确定m的值,使关于x的方程8x2-(2m2+m-6)x+2m-1=0的两根互为相反数.
解:设此方程的两个根为x1、x2,要使方程的两个根互为相反数,必需满足条件:
Δ
x1+x2=0,
x1x2≤0.
0,
得2m2+m-6=0
∴当m=-2时,原方程的两根互为相反数.
例10 方程
有一个正根,一个负根,求m的取值范围。解:由已知,△={即{m>0
m-1<0∴0
X1X2>0
X1+X2>0两个负根△≥0
X1X2>0
X1+X2<0{{{ 一元二次方程 ax2+bx+c=0(a≠0)的两个根
