沪科版数学八下 17.5一元二次方程的应用课件
文档属性
| 名称 | 沪科版数学八下 17.5一元二次方程的应用课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 244.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-03-29 15:35:22 | ||
图片预览






文档简介
课件30张PPT。17.5一元二次方程应用一元一次方程应用题的一般步骤?⒈审清题意,用字母表示一个未知数;⒉找出相等关系;⒊列出需要的代数式,从而列出方程;⒋解这个方程,求出未知数的值;⒌检查求得的答数是否符合应用题的
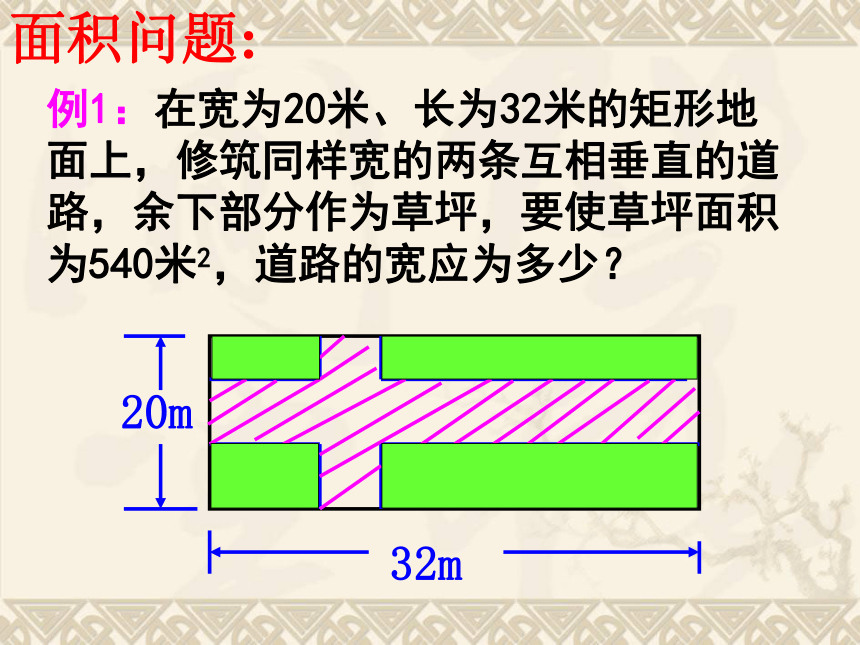
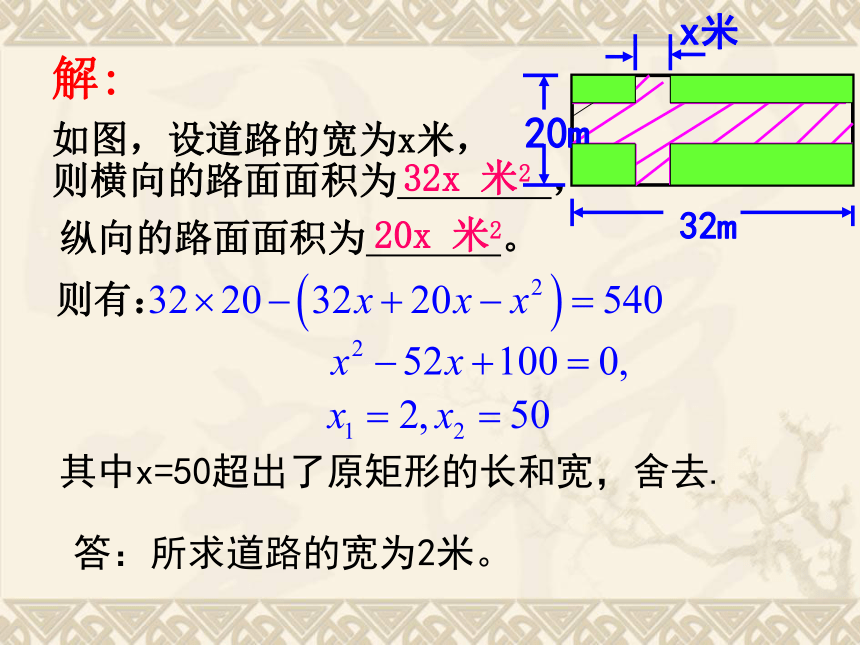
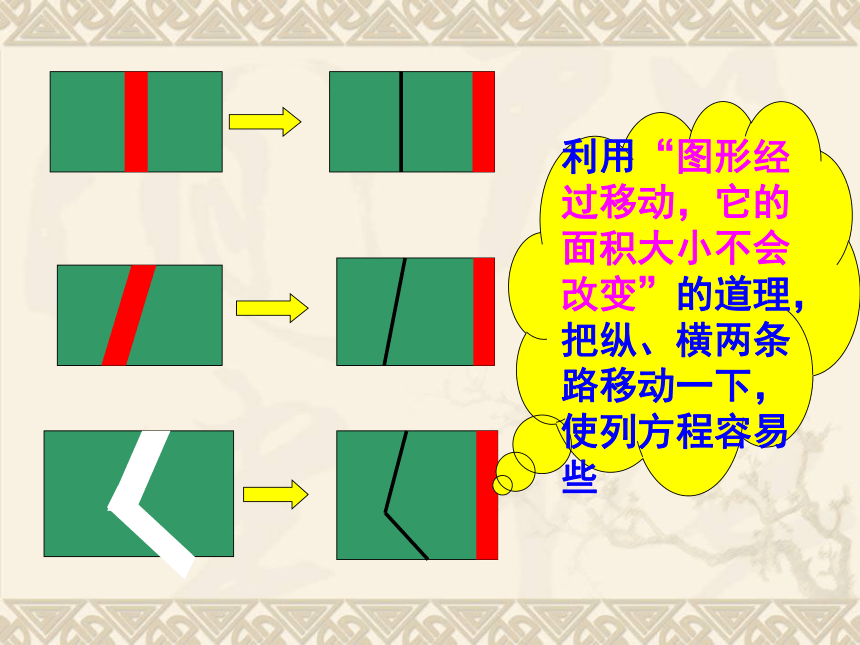
实际意义后,写出答案(及单位名称)。例1:在宽为20米、长为32米的矩形地面上,修筑同样宽的两条互相垂直的道路,余下部分作为草坪,要使草坪面积为540米2,道路的宽应为多少?面积问题:则横向的路面面积为 ,解: 如图,设道路的宽为x米,32x 米2纵向的路面面积为 。20x 米2其中x=50超出了原矩形的长和宽,舍去.答:所求道路的宽为2米。如图,设路宽为x米,耕地矩形的长(横向)为 ,耕地矩形的宽(纵向) 。解法2:(20-x)米(32-x)米试一试:
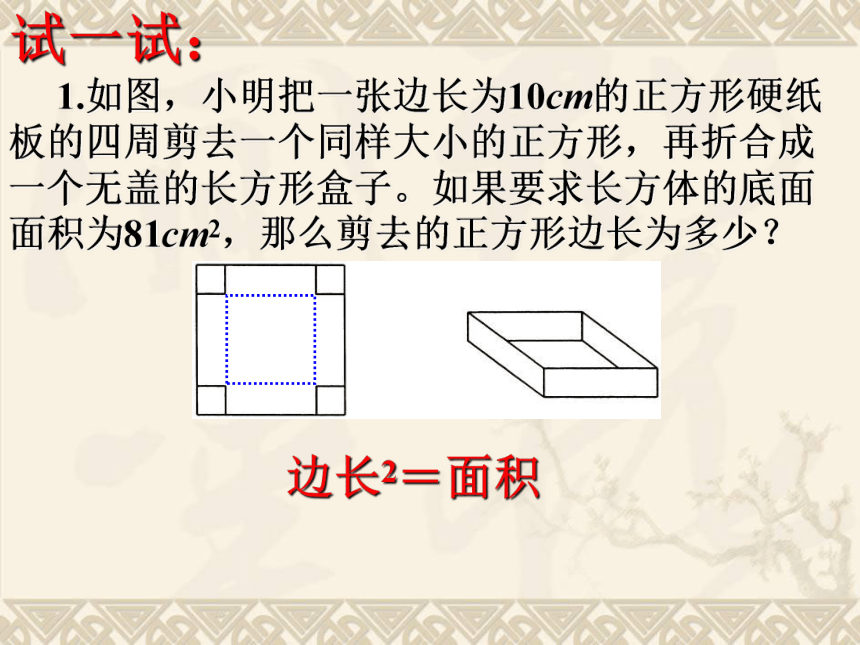
1.如图,小明把一张边长为10cm的正方形硬纸板的四周剪去一个同样大小的正方形,再折合成一个无盖的长方形盒子。如果要求长方体的底面面积为81cm2,那么剪去的正方形边长为多少?边长2=面积 解:设剪去的正方形的边长为 x cm,则长方体的底面边长为___________,依题意得:
(10-2x)2=81
10-2x=±9
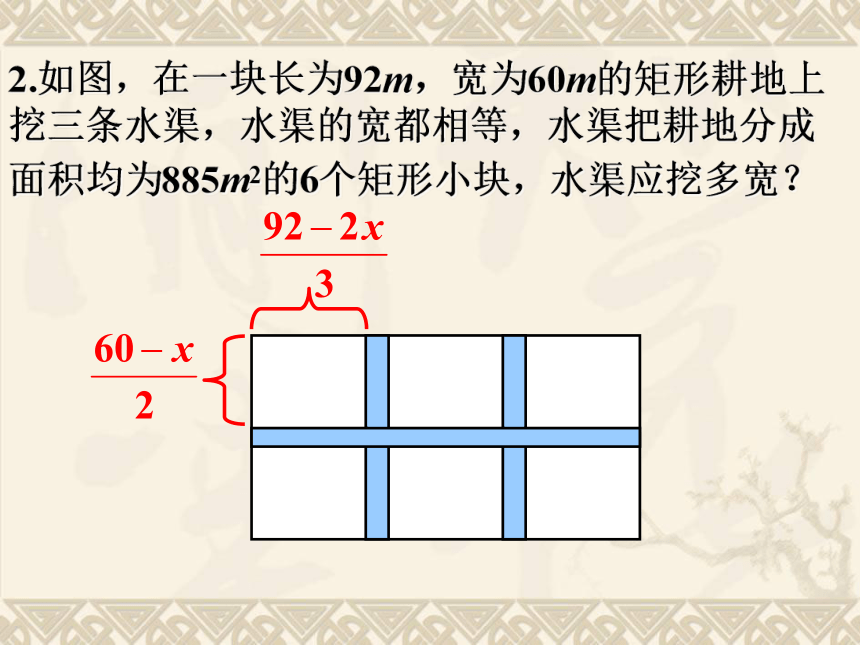
∴x1= x2=(10-2x)cm(不合题意,舍去)答:剪去的正方形的边长为0.5cm。2.如图,在一块长为92m,宽为60m的矩形耕地上挖三条水渠,水渠的宽都相等,水渠把耕地分成面积均为885m2的6个矩形小块,水渠应挖多宽? 解:设水渠应挖 x m宽,则矩形小块的长为 m,宽为 m,依题意得:化为一般形式:x2-106x+105=0
(x-1)(x-105)=0
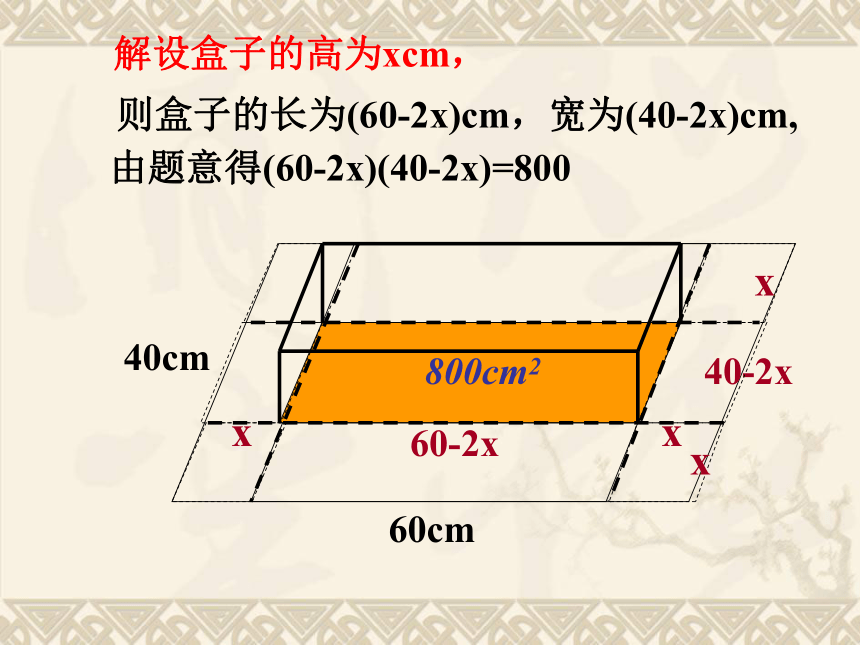
∴x1=1,x2=105(不合题意,舍去)答:水渠应挖 1 m宽。3.某公司因寄内部图纸需要,用一张长60cm,宽40cm的长方形铁皮,四周各剪去一个小的正方形,边折起,制作成一个无盖长方体纸盒,若要求纸盒底部面积为800cm2,
问:纸盒的高应是多少?40cm60cmxxxx60-2x40-2x800cm2解设盒子的高为xcm,则盒子的长为(60-2x)cm,宽为(40-2x)cm,由题意得(60-2x)(40-2x)=800增长(降低)率问题:
例2.某钢铁厂去年1月某种钢的产量为5000吨,3月上升到7200吨,这两个月平均每个月增长的百分率是多少?分析:则2月份比一月份增产________ 吨.
2月份的产量是 _______________吨
3月份比2月份增产____________ 吨
3月份的产量是 ____________ 吨5000(1+x)5000x5000(1+x)x5000(1+x)2解:设平均每个月增长的百分率为x,依题意得
5000(1+x)2 =7200
解得, x1=0.2 x2=-2.2 (不合题意),
答:平均每个月增长的百分率是20%.1.某试验田去年亩产1000斤,今年比去年增产10%,则今年亩产为________斤,计划明年再增产10%,则明年的产量为 斤。
2.某厂一月份产钢50吨,二、三月份的增长率都是x,则该厂三月分产钢______________吨.1100121050(1+x)2增长问题的数量关系是:一次增长:新数 = 基数×(1+增长率)二次增长:新数 = 基数×(1+增长率)2填一填练一练:1、某单位为节省经费,在两个月内将开支从每月1600元降到900元,求这个单位平均每月降低的百分率是多少?1600(1-x)2=9002、某校坚持对学生进行近视眼的防治,近视学生人数逐年减少.据统计,今年的近视学生人数是前年人数的75℅,那么这两年平均每年近视学生人数降低的百分率是多少(精确到1℅)?(1-x)2=0.75提示:增长率问题中若基数不明确,通常设为“1”,或设为a等设为“1”更常用.练一练:3、学校图书馆去年年底有图书5万册,预计到明年年底增加到7.2万册.求这两年的年平均增长率.5(1+x)2=7.24、某种药剂原售价为4元, 经过两次降价, 现在每瓶售价为2.56元,问平均每次降价百分之几? 4(1-x)2=2.56(1)增长率问题 (2)降低率问题 a(1+x)a(1+x)2a(1+x)na(1-x)a(1-x)2a(1-x)n 有一个人患了流感,经过两轮传染后共有121人患了流感,每轮传染中平均一个人传染了几个? 开始有一人患了流感,第一轮的传染源就是这个人,他传染了x个人,用代数式表示,第一轮后共有_______人患了流感; 第二轮传染中,这些人中的每个人又传染
了x个人,用代数式示,第二轮后公
有_______人患了流感. 分析:设每轮传染中平均一个人传染了x个人.探究:列方程1+x+x(1+x)=121解方程,得x1=___________, x2=______________. 平均一个人传染了__________个人.10-1210 如果按照这样的传染速度,三轮传染后有多少人患流感?平均每人传染10人,第二轮传染的人数是110人,第三轮为10×110=1100,三轮共传染了1+10+110+1100=1221人三轮传染的总人数为:( 1 + x ) + x ( 1 + x ) + x · x ( 1 + x )= ( 1+ 10) + 10 ( 1+10 ) + 10×10( 1+ 10)= 11+110+1100=1221数字问题
1.连续整数,后一个数比前一个数多1, 连续奇数或偶数,后一个数比前一个数多2。
2.三位数的表示方法:
三位数=百位数×100 + 十位数×10 + 个位数
其余以此类推。 解:设较小的一个奇数为x,则另一个为x+2, 根据题意得:x(x+2)=323
整理后得:x2+2x-323=0
解这个方程得:x1=17 x2=-19
由x1=17 得:x+2=19
由 x2=-19 得:x+2=-17
答:这两个数奇数是17,19,或者-19,-17。问:如果设这两个数奇数中较小的一个为x-1, 另一个为x+1,这道题该怎么解?例3、两个连续奇数的积是323,求这两个数。1:有一个两位数,它的两个数字之和是8,把这个两位数的数字交换位置后所得的数乘以原来的数就得到1855,求原来的两位数。解:设原来的两位数的个位数为x,
则十位上的数为8-x,根据题意得:
[10(8-x)+x][10x+(8-x)]=1855
整理后得: x2-8x+15=0
解这个方程得:x1=3 x2=5
答:原来的两位数为35或53.练习:2、有一个两位数,十位数字比个位数字大3,而此两位数比这两个数字之积的二倍多5,求这个两位数。解:设个位上的数为x,则十位上的数为 x+3,根据题意得:
10(x+3)+x-2x(x+3)=5
解得: x1=5 x2=- 5/2(舍去)
∴ x+3=8
答:所求两位数为85. 例5: 一组学生组织春游,预计共需费 用120元,后来又有2人参加进来,费用不变,这样每人可少分摊 3元,问原来这组学生的人数是多少?120120xx+2解:设原来这组学生的人数为x人 例5: 一组学生组织春游,预计共需费 用120元,后来又有2人参加进来,费用不变,这样每人可少分摊 3元,问原来这组学生的人数是多少?解:设原来这组学生的人数为x人 经检验,x1=-10 ,x2=8都是原方程的根,但x1=-10不合题意,应舍去,所以x =8答:原来这组学生为8人 例5: 一组学生组织春游,预计共需费 用120元,后来又有2人参加进来,费用不变,这样每人可少分摊 3元,问原来这组学生的人数是多少?120120yy-3解:设原来每人分摊的费用为y元 例5: 一组学生组织春游,预计共需费 用120元,后来又有2人参加进来,费用不变,这样每人可少分摊 3元,问原来这组学生的人数是多少?解:设原来每人分摊的费用为y元 1.某车间要加工170个零件,在加工完90个以后改进了操作方法,每天多加工10个,一共用5天完成了任务,求改进操作方法后每天加工的零件个数.练习: 2.某品牌瓶装饮料每箱价格26元,某商店对该瓶装饮料进行“买一送一”促销活动,若整箱购买,则买一箱送三瓶,这相当于每瓶比原价便宜了0.6元,问该品牌饮料一箱有多少瓶?2626yy+3解:设该品牌饮料一箱有y瓶
实际意义后,写出答案(及单位名称)。例1:在宽为20米、长为32米的矩形地面上,修筑同样宽的两条互相垂直的道路,余下部分作为草坪,要使草坪面积为540米2,道路的宽应为多少?面积问题:则横向的路面面积为 ,解: 如图,设道路的宽为x米,32x 米2纵向的路面面积为 。20x 米2其中x=50超出了原矩形的长和宽,舍去.答:所求道路的宽为2米。如图,设路宽为x米,耕地矩形的长(横向)为 ,耕地矩形的宽(纵向) 。解法2:(20-x)米(32-x)米试一试:
1.如图,小明把一张边长为10cm的正方形硬纸板的四周剪去一个同样大小的正方形,再折合成一个无盖的长方形盒子。如果要求长方体的底面面积为81cm2,那么剪去的正方形边长为多少?边长2=面积 解:设剪去的正方形的边长为 x cm,则长方体的底面边长为___________,依题意得:
(10-2x)2=81
10-2x=±9
∴x1= x2=(10-2x)cm(不合题意,舍去)答:剪去的正方形的边长为0.5cm。2.如图,在一块长为92m,宽为60m的矩形耕地上挖三条水渠,水渠的宽都相等,水渠把耕地分成面积均为885m2的6个矩形小块,水渠应挖多宽? 解:设水渠应挖 x m宽,则矩形小块的长为 m,宽为 m,依题意得:化为一般形式:x2-106x+105=0
(x-1)(x-105)=0
∴x1=1,x2=105(不合题意,舍去)答:水渠应挖 1 m宽。3.某公司因寄内部图纸需要,用一张长60cm,宽40cm的长方形铁皮,四周各剪去一个小的正方形,边折起,制作成一个无盖长方体纸盒,若要求纸盒底部面积为800cm2,
问:纸盒的高应是多少?40cm60cmxxxx60-2x40-2x800cm2解设盒子的高为xcm,则盒子的长为(60-2x)cm,宽为(40-2x)cm,由题意得(60-2x)(40-2x)=800增长(降低)率问题:
例2.某钢铁厂去年1月某种钢的产量为5000吨,3月上升到7200吨,这两个月平均每个月增长的百分率是多少?分析:则2月份比一月份增产________ 吨.
2月份的产量是 _______________吨
3月份比2月份增产____________ 吨
3月份的产量是 ____________ 吨5000(1+x)5000x5000(1+x)x5000(1+x)2解:设平均每个月增长的百分率为x,依题意得
5000(1+x)2 =7200
解得, x1=0.2 x2=-2.2 (不合题意),
答:平均每个月增长的百分率是20%.1.某试验田去年亩产1000斤,今年比去年增产10%,则今年亩产为________斤,计划明年再增产10%,则明年的产量为 斤。
2.某厂一月份产钢50吨,二、三月份的增长率都是x,则该厂三月分产钢______________吨.1100121050(1+x)2增长问题的数量关系是:一次增长:新数 = 基数×(1+增长率)二次增长:新数 = 基数×(1+增长率)2填一填练一练:1、某单位为节省经费,在两个月内将开支从每月1600元降到900元,求这个单位平均每月降低的百分率是多少?1600(1-x)2=9002、某校坚持对学生进行近视眼的防治,近视学生人数逐年减少.据统计,今年的近视学生人数是前年人数的75℅,那么这两年平均每年近视学生人数降低的百分率是多少(精确到1℅)?(1-x)2=0.75提示:增长率问题中若基数不明确,通常设为“1”,或设为a等设为“1”更常用.练一练:3、学校图书馆去年年底有图书5万册,预计到明年年底增加到7.2万册.求这两年的年平均增长率.5(1+x)2=7.24、某种药剂原售价为4元, 经过两次降价, 现在每瓶售价为2.56元,问平均每次降价百分之几? 4(1-x)2=2.56(1)增长率问题 (2)降低率问题 a(1+x)a(1+x)2a(1+x)na(1-x)a(1-x)2a(1-x)n 有一个人患了流感,经过两轮传染后共有121人患了流感,每轮传染中平均一个人传染了几个? 开始有一人患了流感,第一轮的传染源就是这个人,他传染了x个人,用代数式表示,第一轮后共有_______人患了流感; 第二轮传染中,这些人中的每个人又传染
了x个人,用代数式示,第二轮后公
有_______人患了流感. 分析:设每轮传染中平均一个人传染了x个人.探究:列方程1+x+x(1+x)=121解方程,得x1=___________, x2=______________. 平均一个人传染了__________个人.10-1210 如果按照这样的传染速度,三轮传染后有多少人患流感?平均每人传染10人,第二轮传染的人数是110人,第三轮为10×110=1100,三轮共传染了1+10+110+1100=1221人三轮传染的总人数为:( 1 + x ) + x ( 1 + x ) + x · x ( 1 + x )= ( 1+ 10) + 10 ( 1+10 ) + 10×10( 1+ 10)= 11+110+1100=1221数字问题
1.连续整数,后一个数比前一个数多1, 连续奇数或偶数,后一个数比前一个数多2。
2.三位数的表示方法:
三位数=百位数×100 + 十位数×10 + 个位数
其余以此类推。 解:设较小的一个奇数为x,则另一个为x+2, 根据题意得:x(x+2)=323
整理后得:x2+2x-323=0
解这个方程得:x1=17 x2=-19
由x1=17 得:x+2=19
由 x2=-19 得:x+2=-17
答:这两个数奇数是17,19,或者-19,-17。问:如果设这两个数奇数中较小的一个为x-1, 另一个为x+1,这道题该怎么解?例3、两个连续奇数的积是323,求这两个数。1:有一个两位数,它的两个数字之和是8,把这个两位数的数字交换位置后所得的数乘以原来的数就得到1855,求原来的两位数。解:设原来的两位数的个位数为x,
则十位上的数为8-x,根据题意得:
[10(8-x)+x][10x+(8-x)]=1855
整理后得: x2-8x+15=0
解这个方程得:x1=3 x2=5
答:原来的两位数为35或53.练习:2、有一个两位数,十位数字比个位数字大3,而此两位数比这两个数字之积的二倍多5,求这个两位数。解:设个位上的数为x,则十位上的数为 x+3,根据题意得:
10(x+3)+x-2x(x+3)=5
解得: x1=5 x2=- 5/2(舍去)
∴ x+3=8
答:所求两位数为85. 例5: 一组学生组织春游,预计共需费 用120元,后来又有2人参加进来,费用不变,这样每人可少分摊 3元,问原来这组学生的人数是多少?120120xx+2解:设原来这组学生的人数为x人 例5: 一组学生组织春游,预计共需费 用120元,后来又有2人参加进来,费用不变,这样每人可少分摊 3元,问原来这组学生的人数是多少?解:设原来这组学生的人数为x人 经检验,x1=-10 ,x2=8都是原方程的根,但x1=-10不合题意,应舍去,所以x =8答:原来这组学生为8人 例5: 一组学生组织春游,预计共需费 用120元,后来又有2人参加进来,费用不变,这样每人可少分摊 3元,问原来这组学生的人数是多少?120120yy-3解:设原来每人分摊的费用为y元 例5: 一组学生组织春游,预计共需费 用120元,后来又有2人参加进来,费用不变,这样每人可少分摊 3元,问原来这组学生的人数是多少?解:设原来每人分摊的费用为y元 1.某车间要加工170个零件,在加工完90个以后改进了操作方法,每天多加工10个,一共用5天完成了任务,求改进操作方法后每天加工的零件个数.练习: 2.某品牌瓶装饮料每箱价格26元,某商店对该瓶装饮料进行“买一送一”促销活动,若整箱购买,则买一箱送三瓶,这相当于每瓶比原价便宜了0.6元,问该品牌饮料一箱有多少瓶?2626yy+3解:设该品牌饮料一箱有y瓶
