2023年河南省普通高中学业水平考试数学仿真模拟卷(三)(2月)(Word版含答案)
文档属性
| 名称 | 2023年河南省普通高中学业水平考试数学仿真模拟卷(三)(2月)(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 92.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-22 00:00:00 | ||
图片预览



文档简介
河南省普通高中学业水平考试(2019版新教材)
数学仿真模拟卷(三)
一、选择题(本大题共16小题,每题3分,共48分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.已知全集U=R,A={x|x≤0},B={x|x≥1},则集合 U(A∪B)=( )
A.{x|x≥0} B.{x|x≤1} C.{x|0≤x≤1} D.{x|02.“x2-4x-5=0”是“x=5”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
3.函数y=在[2,3]上的最小值为( )
A.2 B. C. D.-
4.已知某圆台的一个底面周长是另一个底面周长的3倍,母线长为3,圆台的侧面积为84π,则该圆台较小底面的半径为( )
A.7 B.6 C.5 D.3
5.在△ABC中,若a=2,b=2,A=30°,则B为( )
A.60° B.60°或120° C.30° D.30°或150°
6.已知f(x)是偶函数,且在区间[0,+∞)上是增函数,则f(-0.5),f(-1),f(0)的大小关系是( )
A.f(-0.5)<f(0)<f(-1) B.f(-1)<f(-0.5)<f(0)
C.f(0)<f(-0.5)<f(-1) D.f(-1)<f(0)<f(-0.5)
7.某高三学生在连续五次月考中的数学成绩(单位:分)为:90,90,93,94,93,则该学生在这五次月考中数学成绩数据的平均数和方差分别为( )
A.92,2.8 B.92,2 C.93,2 D.93,2.8
8.若连续抛掷两次骰子得到的点数分别为m,n,则点P(m,n)在一次函数y=-x+4图象上的概率是( )
A. B. C. D.
9.下列函数中,在区间(0,+∞)上为增函数的是( )
A.y= B.y= C.y=log3x D.y=(x-1)2
10.函数f(x)=2x-的零点所在的区间是( )
A.(1,+∞) B. C. D.
11.已知,sin α-cos α=,则sin 2α的值为( )
A. B. C.- D.-
12.若P是两条异面直线l,m外的任意一点,则( )
A.过点P有且仅有一条直线与l,m都平行
B.过点P有且仅有一条直线与l,m都垂直
C.过点P有且仅有一条直线与l,m都相交
D.过点P有且仅有一条直线与l,m都异面
13.在△ABC中,=c,=b,若点D满足=2,以b与c作为基底,则=( )
A. b+c B. c-b C. b-c D. b+c
14.一元二次方程ax2+bx+c=0的两根为-2,3,a<0,那么ax2+bx+c>0的解集为( )
A.{x|x>3或x<-2} B.{x|x>2或x<-3}
C.{x|-215.已知点P(1,a)在角α的终边上,tan=-,则实数a的值是( )
A.2 B. C.-2 D.-
16.设函数f(x)=sin(ω>0,|φ|<)的最小正周期为π,且是偶函数,则( )
A.f(x)在单调递减 B.f(x)在单调递减
C.f(x)在单调递增 D.f(x)在单调递增
二、填空题(本大题共7小题,每小题3分,共21分)
17.已知a=(1,),b=(-2,0),则|a+b|=________.
18.若x2+y2=4,则xy的最大值为________.
19.在△ABC中,sin A=,则角A=________.
20.如图所示是一容量为100的样本的频率分布直方图,
则由图中的数据可知,样本落在[15,20]内的频数为_____.
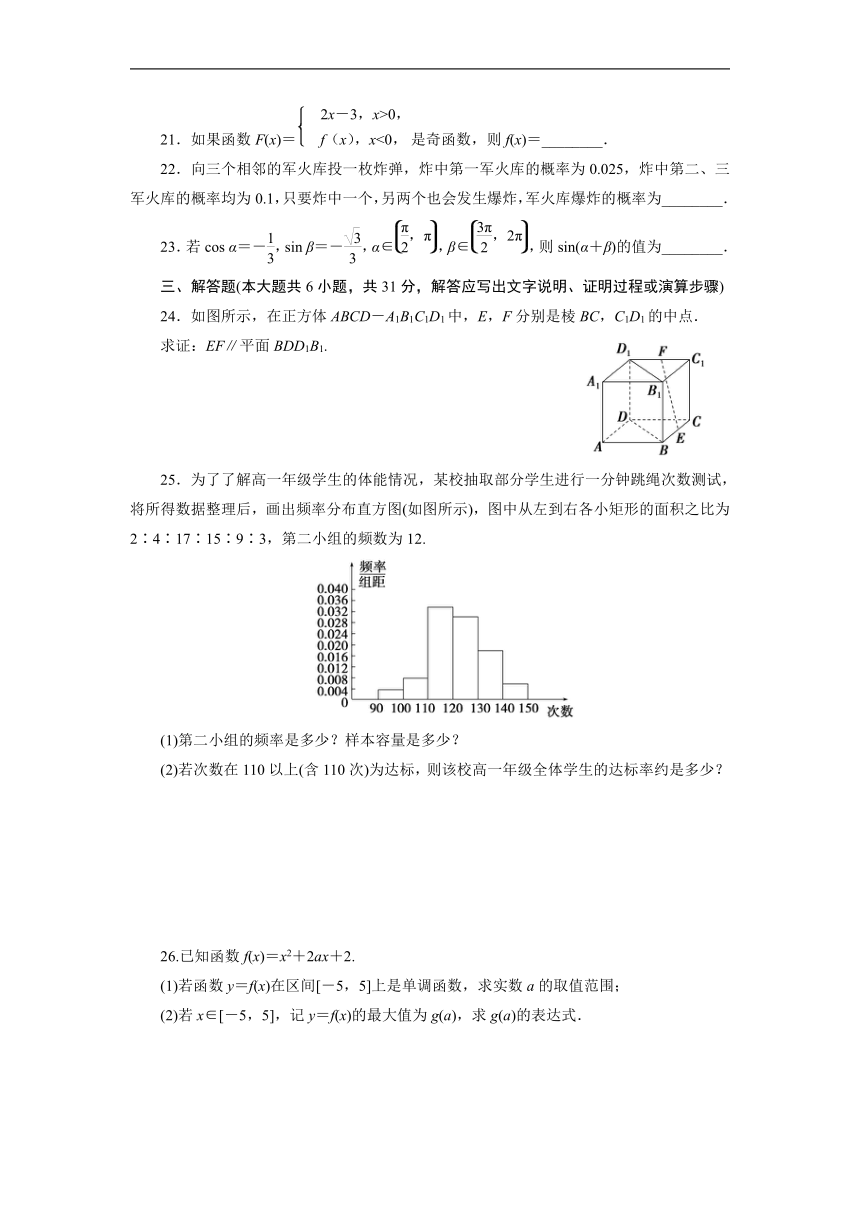
21.如果函数F(x)=是奇函数,则f(x)=________.
22.向三个相邻的军火库投一枚炸弹,炸中第一军火库的概率为0.025,炸中第二、三军火库的概率均为0.1,只要炸中一个,另两个也会发生爆炸,军火库爆炸的概率为________.
23.若cos α=-,sin β=-,α∈,β∈,则sin(α+β)的值为________.
三、解答题(本大题共6小题,共31分,解答应写出文字说明、证明过程或演算步骤)
24.如图所示,在正方体ABCD-A1B1C1D1中,E,F分别是棱BC,C1D1的中点.
求证:EF∥平面BDD1B1.
25.为了了解高一年级学生的体能情况,某校抽取部分学生进行一分钟跳绳次数测试,将所得数据整理后,画出频率分布直方图(如图所示),图中从左到右各小矩形的面积之比为2∶4∶17∶15∶9∶3,第二小组的频数为12.
(1)第二小组的频率是多少?样本容量是多少?
(2)若次数在110以上(含110次)为达标,则该校高一年级全体学生的达标率约是多少?
26.已知函数f(x)=x2+2ax+2.
(1)若函数y=f(x)在区间[-5,5]上是单调函数,求实数a的取值范围;
(2)若x∈[-5,5],记y=f(x)的最大值为g(a),求g(a)的表达式.
27.已知向量a,b,c是同一平面内的三个向量,其中a=(1,-1).
(1)若|c|=3,且c∥a,求向量c的坐标;
(2)若b是单位向量,且a⊥(a-2b),求a与b的夹角θ.
28.设△ABC的内角A,B,C的对边分别为a,b,c,且bsin A=acos B.
(1)求B的大小;
(2)若b=3,sin C=2sin A,求a,c的值.
29.已知函数某旅游爱好者计划从3个亚洲国家A1,A2,A3和3个欧洲国家B1,B2,B3中选择2个国家去旅游.
(1)若从这6个国家中任选2个,求这2个国家都是亚洲国家的概率;
(2)若从亚洲国家和欧洲国家中各任选1个,求这2个国家包括A1但不包括B1的概率.
仿真模拟卷(三)答案
1.解析:选D 由题意可知,A∪B={x|x≤0,或x≥1},所以 U(A∪B)={x|0<x<1}.故选D.
2.解析:选B 由x2-4x-5=0得x=5或x=-1,则当x=5时,x2-4x-5=0成立,但x2-4x-5=0时,x=5不一定成立,故选B.
3.解析:选B ∵函数y=在[2,3]上单调递减,∴当x=3时,ymin==.故选B.
4.解析:选A 设圆台较小底面的半径为r,则另一底面的半径为3r.由S侧=3π(r+3r)=84π,解得r=7.故选A.
5.解析:选B 由正弦定理可知=,
∴sin B===,∵0°<B<180°,b>a,∴B=60°或120°.故选B.
6.解析:选C ∵函数f(x)为偶函数,∴f(-0.5)=f(0.5),f(-1)=f(1).又∵f(x)在区间[0,+∞)上是增函数,∴f(0)<f(0.5)<f(1),即f(0)<f(-0.5)<f(-1).故选C.
7.解析:选A 该学生在这五次月考中数学成绩数据的平均数为x=×(90+90+93+94+93)=92,
方差为s2=×[(90-92)2+(90-92)2+(93-92)2+(94-92)2+(93-92)2]=2.8.故选A.
8.解析:选D 由题意(m,n)的取值情况有(1,1),(1,2),…,(1,6);(2,1),(2,2),…,(2,6);…;(6,1),(6,2),…,(6,6),共36种,而满足点P(m,n)在一次函数y=-x+4图象上的取值情况有(1,3),(2,2),(3,1),共3种.故所求概率为=.故选D.
9.解析:选C 根据题意,依次分析选项:
对于A,y=,是指数函数,在R上是减函数,不符合题意;对于B,y=,是反比例函数,在(0,+∞)上是减函数,不符合题意;对于C,y=log3x,是对数函数,在区间(0,+∞)上为增函数,符合题意;对于D,y=(x-1)2,是二次函数,在区间(0,1)上是减函数,不符合题意.故选C.
10.解析:选B 由f(x)=2x-,得
f =2 -2<0,f(1)=2-1=1>0,
∴f ·f(1)<0,
∴零点所在区间为.故选B.
11.解析:选B 由于sin α-cos α=,
所以(sin α-cos α)2=,即1-2sin αcos α=,
整理得sin 2α=.故选B.
12.解析:选B 逐个分析,过点P与l,m都平行的直线不存在;过点P与l,m都垂直的直线只有一条;过点P与l,m都相交的直线1条或0条;过点P与l,m都异面的直线有无数条.故选B.
13.解析:选A ∵=2,∴-=2(-),∴-c=2(b-),∴=c+b.故选A.
14.解析:选C 由题意知,-2+3=-,-2×3=,∴b=-a,c=-6a,
∴ax2+bx+c=ax2-ax-6a>0,
∵a<0,∴x2-x-6<0,
∴(x-3)(x+2)<0,∴-215.解析:选C ∵tan===-,
∴tan α=-2,
∵点P(1,a)在角α的终边上,
∴tan α==a,∴a=-2.故选C.
16.解析:选A 由条件知ω=2.
∵f(x)是偶函数且|φ|<,∴φ=,
这时f(x)=sin=cos 2x.
∵x∈时,2x∈(0,π),
∴f(x)在上单调递减.故选A.
17.解析: 因为a+b=(-1,),所以|a+b|==2.
答案:2
18.解析:xy≤=2,当且仅当x=y时,等号成立.
答案:2
19.解析:由题意知cos A>0,即A为锐角.
将sin A=两边平方得2sin2A=3cos A,即2(1-cos2A)=3cos A,
∴2cos2A+3cos A-2=0,
解得cos A=或cos A=-2(舍去),
∴A=.
答案:
20.解析:样本数据落在[15,20]内的频数为100×[1-5×(0.04+0.1)]=30.
答案:30
21.解析:当x<0时,-x>0,F(-x)=-2x-3,
又∵F(x)为奇函数,∴F(-x)=-F(x),
∴F(x)=2x+3,即f(x)=2x+3.
答案:2x+3
22.解析:设A,B,C分别表示炸弹炸中第一、第二、第三军火库这三个事件,D表示军火库爆炸,则P(A)=0.025,P(B)=0.1,P(C)=0.1,其中A,B,C互斥,根据概率加法公式得P(D)=P(A∪B∪C)=P(A)+P(B)+P(C)=0.025+0.1+0.1=0.225.
答案:0.225
23.解析:∵cos α=-,α∈,
∴sin α==.
∵sin β=-,β∈,
∴cos β==,
∴sin(α+β)=sin αcos β+cos αsin β
=×+×=.
答案:
24.证明:取D1B1的中点O,连接OF,OB(图略).
∵F为C1D1的中点,
∴OF∥B1C1且OF=B1C1,
又BE∥B1C1,BE=B1C1,
∴OF∥BE且OF=BE,
∴四边形OFEB是平行四边形,∴EF∥BO.
∵EF 平面BDD1B1,BO 平面BDD1B1,
∴EF∥平面BDD1B1.
25.解:(1)频率分布直方图是以面积的形式来反映数据落在各小组内的频率大小的,
因此第二小组的频率为=0.08.
因为第二小组的频率=,
所以样本容量===150.
(2)由频率分布直方图可知该校高一年级全体学生的达标率约为×100%=88%.
26.解:(1)∵函数f(x)=x2+2ax+2,
∴对称轴x=-a,根据二次函数的性质得出:
当-a≤-5或-a≥5时,f(x)在[-5,5]上单调,即a≥5或a≤-5.
故实数a的取值范围为(-∞,-5]∪[5,+∞).
(2)对称轴x=-a,当-a≤0,即a≥0时,最大值g(a)=f(5)=27+10a;
当-a>0,即a<0时,最大值g(a)=f(-5)=27-10a.
综上,g(a)=
27.解:(1)设c=(x,y),由|c|=3,c∥a可得
所以或
故c=(-3,3)或c=(3,-3).
(2)因为|a|=,且a⊥(a-2b),所以a·(a-2b)=0,
即a2-2a·b=0,所以a·b=1,
故cos θ==,
因为θ∈[0,π],
所以θ=.
28.解:(1)∵bsin A=acos B,
∴由正弦定理,得sin Bsin A=sin Acos B.
在△ABC中,sin A≠0,
即得tan B=,∴B=.
(2)∵sin C=2sin A,∴由正弦定理,得c=2a,
由余弦定理b2=a2+c2-2accos B,
即9=a2+4a2-2a·2acos,
解得a=,∴c=2a=2.
29.解:(1)由题意知,从6个国家中任选2个国家,其一切可能的结果有(A1,A2),(A1,A3),(A1,B1),(A1,B2),(A1,B3),(A2,A3),(A2,B1),(A2,B2),(A2,B3),(A3,B1),(A3,B2),(A3,B3),(B1,B2),(B1,B3),(B2,B3),共15个.
所选2个国家都是亚洲国家的事件所包含的样本点有(A1,A2),(A1,A3),(A2,A3),共3个,
则所求事件的概率为P==.
(2)从亚洲国家和欧洲国家中各任选1个,其一切可能的结果有(A1,B1),(A1,B2),(A1,B3),(A2,B1),(A2,B2),(A2,B3),(A3,B1),(A3,B2),(A3,B3),共9个.
包括A1但不包括B1的事件所包含的样本点有
(A1,B2),(A1,B3),共2个,
则所求事件的概率为P=.
数学仿真模拟卷(三)
一、选择题(本大题共16小题,每题3分,共48分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.已知全集U=R,A={x|x≤0},B={x|x≥1},则集合 U(A∪B)=( )
A.{x|x≥0} B.{x|x≤1} C.{x|0≤x≤1} D.{x|0
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
3.函数y=在[2,3]上的最小值为( )
A.2 B. C. D.-
4.已知某圆台的一个底面周长是另一个底面周长的3倍,母线长为3,圆台的侧面积为84π,则该圆台较小底面的半径为( )
A.7 B.6 C.5 D.3
5.在△ABC中,若a=2,b=2,A=30°,则B为( )
A.60° B.60°或120° C.30° D.30°或150°
6.已知f(x)是偶函数,且在区间[0,+∞)上是增函数,则f(-0.5),f(-1),f(0)的大小关系是( )
A.f(-0.5)<f(0)<f(-1) B.f(-1)<f(-0.5)<f(0)
C.f(0)<f(-0.5)<f(-1) D.f(-1)<f(0)<f(-0.5)
7.某高三学生在连续五次月考中的数学成绩(单位:分)为:90,90,93,94,93,则该学生在这五次月考中数学成绩数据的平均数和方差分别为( )
A.92,2.8 B.92,2 C.93,2 D.93,2.8
8.若连续抛掷两次骰子得到的点数分别为m,n,则点P(m,n)在一次函数y=-x+4图象上的概率是( )
A. B. C. D.
9.下列函数中,在区间(0,+∞)上为增函数的是( )
A.y= B.y= C.y=log3x D.y=(x-1)2
10.函数f(x)=2x-的零点所在的区间是( )
A.(1,+∞) B. C. D.
11.已知,sin α-cos α=,则sin 2α的值为( )
A. B. C.- D.-
12.若P是两条异面直线l,m外的任意一点,则( )
A.过点P有且仅有一条直线与l,m都平行
B.过点P有且仅有一条直线与l,m都垂直
C.过点P有且仅有一条直线与l,m都相交
D.过点P有且仅有一条直线与l,m都异面
13.在△ABC中,=c,=b,若点D满足=2,以b与c作为基底,则=( )
A. b+c B. c-b C. b-c D. b+c
14.一元二次方程ax2+bx+c=0的两根为-2,3,a<0,那么ax2+bx+c>0的解集为( )
A.{x|x>3或x<-2} B.{x|x>2或x<-3}
C.{x|-2
A.2 B. C.-2 D.-
16.设函数f(x)=sin(ω>0,|φ|<)的最小正周期为π,且是偶函数,则( )
A.f(x)在单调递减 B.f(x)在单调递减
C.f(x)在单调递增 D.f(x)在单调递增
二、填空题(本大题共7小题,每小题3分,共21分)
17.已知a=(1,),b=(-2,0),则|a+b|=________.
18.若x2+y2=4,则xy的最大值为________.
19.在△ABC中,sin A=,则角A=________.
20.如图所示是一容量为100的样本的频率分布直方图,
则由图中的数据可知,样本落在[15,20]内的频数为_____.
21.如果函数F(x)=是奇函数,则f(x)=________.
22.向三个相邻的军火库投一枚炸弹,炸中第一军火库的概率为0.025,炸中第二、三军火库的概率均为0.1,只要炸中一个,另两个也会发生爆炸,军火库爆炸的概率为________.
23.若cos α=-,sin β=-,α∈,β∈,则sin(α+β)的值为________.
三、解答题(本大题共6小题,共31分,解答应写出文字说明、证明过程或演算步骤)
24.如图所示,在正方体ABCD-A1B1C1D1中,E,F分别是棱BC,C1D1的中点.
求证:EF∥平面BDD1B1.
25.为了了解高一年级学生的体能情况,某校抽取部分学生进行一分钟跳绳次数测试,将所得数据整理后,画出频率分布直方图(如图所示),图中从左到右各小矩形的面积之比为2∶4∶17∶15∶9∶3,第二小组的频数为12.
(1)第二小组的频率是多少?样本容量是多少?
(2)若次数在110以上(含110次)为达标,则该校高一年级全体学生的达标率约是多少?
26.已知函数f(x)=x2+2ax+2.
(1)若函数y=f(x)在区间[-5,5]上是单调函数,求实数a的取值范围;
(2)若x∈[-5,5],记y=f(x)的最大值为g(a),求g(a)的表达式.
27.已知向量a,b,c是同一平面内的三个向量,其中a=(1,-1).
(1)若|c|=3,且c∥a,求向量c的坐标;
(2)若b是单位向量,且a⊥(a-2b),求a与b的夹角θ.
28.设△ABC的内角A,B,C的对边分别为a,b,c,且bsin A=acos B.
(1)求B的大小;
(2)若b=3,sin C=2sin A,求a,c的值.
29.已知函数某旅游爱好者计划从3个亚洲国家A1,A2,A3和3个欧洲国家B1,B2,B3中选择2个国家去旅游.
(1)若从这6个国家中任选2个,求这2个国家都是亚洲国家的概率;
(2)若从亚洲国家和欧洲国家中各任选1个,求这2个国家包括A1但不包括B1的概率.
仿真模拟卷(三)答案
1.解析:选D 由题意可知,A∪B={x|x≤0,或x≥1},所以 U(A∪B)={x|0<x<1}.故选D.
2.解析:选B 由x2-4x-5=0得x=5或x=-1,则当x=5时,x2-4x-5=0成立,但x2-4x-5=0时,x=5不一定成立,故选B.
3.解析:选B ∵函数y=在[2,3]上单调递减,∴当x=3时,ymin==.故选B.
4.解析:选A 设圆台较小底面的半径为r,则另一底面的半径为3r.由S侧=3π(r+3r)=84π,解得r=7.故选A.
5.解析:选B 由正弦定理可知=,
∴sin B===,∵0°<B<180°,b>a,∴B=60°或120°.故选B.
6.解析:选C ∵函数f(x)为偶函数,∴f(-0.5)=f(0.5),f(-1)=f(1).又∵f(x)在区间[0,+∞)上是增函数,∴f(0)<f(0.5)<f(1),即f(0)<f(-0.5)<f(-1).故选C.
7.解析:选A 该学生在这五次月考中数学成绩数据的平均数为x=×(90+90+93+94+93)=92,
方差为s2=×[(90-92)2+(90-92)2+(93-92)2+(94-92)2+(93-92)2]=2.8.故选A.
8.解析:选D 由题意(m,n)的取值情况有(1,1),(1,2),…,(1,6);(2,1),(2,2),…,(2,6);…;(6,1),(6,2),…,(6,6),共36种,而满足点P(m,n)在一次函数y=-x+4图象上的取值情况有(1,3),(2,2),(3,1),共3种.故所求概率为=.故选D.
9.解析:选C 根据题意,依次分析选项:
对于A,y=,是指数函数,在R上是减函数,不符合题意;对于B,y=,是反比例函数,在(0,+∞)上是减函数,不符合题意;对于C,y=log3x,是对数函数,在区间(0,+∞)上为增函数,符合题意;对于D,y=(x-1)2,是二次函数,在区间(0,1)上是减函数,不符合题意.故选C.
10.解析:选B 由f(x)=2x-,得
f =2 -2<0,f(1)=2-1=1>0,
∴f ·f(1)<0,
∴零点所在区间为.故选B.
11.解析:选B 由于sin α-cos α=,
所以(sin α-cos α)2=,即1-2sin αcos α=,
整理得sin 2α=.故选B.
12.解析:选B 逐个分析,过点P与l,m都平行的直线不存在;过点P与l,m都垂直的直线只有一条;过点P与l,m都相交的直线1条或0条;过点P与l,m都异面的直线有无数条.故选B.
13.解析:选A ∵=2,∴-=2(-),∴-c=2(b-),∴=c+b.故选A.
14.解析:选C 由题意知,-2+3=-,-2×3=,∴b=-a,c=-6a,
∴ax2+bx+c=ax2-ax-6a>0,
∵a<0,∴x2-x-6<0,
∴(x-3)(x+2)<0,∴-2
∴tan α=-2,
∵点P(1,a)在角α的终边上,
∴tan α==a,∴a=-2.故选C.
16.解析:选A 由条件知ω=2.
∵f(x)是偶函数且|φ|<,∴φ=,
这时f(x)=sin=cos 2x.
∵x∈时,2x∈(0,π),
∴f(x)在上单调递减.故选A.
17.解析: 因为a+b=(-1,),所以|a+b|==2.
答案:2
18.解析:xy≤=2,当且仅当x=y时,等号成立.
答案:2
19.解析:由题意知cos A>0,即A为锐角.
将sin A=两边平方得2sin2A=3cos A,即2(1-cos2A)=3cos A,
∴2cos2A+3cos A-2=0,
解得cos A=或cos A=-2(舍去),
∴A=.
答案:
20.解析:样本数据落在[15,20]内的频数为100×[1-5×(0.04+0.1)]=30.
答案:30
21.解析:当x<0时,-x>0,F(-x)=-2x-3,
又∵F(x)为奇函数,∴F(-x)=-F(x),
∴F(x)=2x+3,即f(x)=2x+3.
答案:2x+3
22.解析:设A,B,C分别表示炸弹炸中第一、第二、第三军火库这三个事件,D表示军火库爆炸,则P(A)=0.025,P(B)=0.1,P(C)=0.1,其中A,B,C互斥,根据概率加法公式得P(D)=P(A∪B∪C)=P(A)+P(B)+P(C)=0.025+0.1+0.1=0.225.
答案:0.225
23.解析:∵cos α=-,α∈,
∴sin α==.
∵sin β=-,β∈,
∴cos β==,
∴sin(α+β)=sin αcos β+cos αsin β
=×+×=.
答案:
24.证明:取D1B1的中点O,连接OF,OB(图略).
∵F为C1D1的中点,
∴OF∥B1C1且OF=B1C1,
又BE∥B1C1,BE=B1C1,
∴OF∥BE且OF=BE,
∴四边形OFEB是平行四边形,∴EF∥BO.
∵EF 平面BDD1B1,BO 平面BDD1B1,
∴EF∥平面BDD1B1.
25.解:(1)频率分布直方图是以面积的形式来反映数据落在各小组内的频率大小的,
因此第二小组的频率为=0.08.
因为第二小组的频率=,
所以样本容量===150.
(2)由频率分布直方图可知该校高一年级全体学生的达标率约为×100%=88%.
26.解:(1)∵函数f(x)=x2+2ax+2,
∴对称轴x=-a,根据二次函数的性质得出:
当-a≤-5或-a≥5时,f(x)在[-5,5]上单调,即a≥5或a≤-5.
故实数a的取值范围为(-∞,-5]∪[5,+∞).
(2)对称轴x=-a,当-a≤0,即a≥0时,最大值g(a)=f(5)=27+10a;
当-a>0,即a<0时,最大值g(a)=f(-5)=27-10a.
综上,g(a)=
27.解:(1)设c=(x,y),由|c|=3,c∥a可得
所以或
故c=(-3,3)或c=(3,-3).
(2)因为|a|=,且a⊥(a-2b),所以a·(a-2b)=0,
即a2-2a·b=0,所以a·b=1,
故cos θ==,
因为θ∈[0,π],
所以θ=.
28.解:(1)∵bsin A=acos B,
∴由正弦定理,得sin Bsin A=sin Acos B.
在△ABC中,sin A≠0,
即得tan B=,∴B=.
(2)∵sin C=2sin A,∴由正弦定理,得c=2a,
由余弦定理b2=a2+c2-2accos B,
即9=a2+4a2-2a·2acos,
解得a=,∴c=2a=2.
29.解:(1)由题意知,从6个国家中任选2个国家,其一切可能的结果有(A1,A2),(A1,A3),(A1,B1),(A1,B2),(A1,B3),(A2,A3),(A2,B1),(A2,B2),(A2,B3),(A3,B1),(A3,B2),(A3,B3),(B1,B2),(B1,B3),(B2,B3),共15个.
所选2个国家都是亚洲国家的事件所包含的样本点有(A1,A2),(A1,A3),(A2,A3),共3个,
则所求事件的概率为P==.
(2)从亚洲国家和欧洲国家中各任选1个,其一切可能的结果有(A1,B1),(A1,B2),(A1,B3),(A2,B1),(A2,B2),(A2,B3),(A3,B1),(A3,B2),(A3,B3),共9个.
包括A1但不包括B1的事件所包含的样本点有
(A1,B2),(A1,B3),共2个,
则所求事件的概率为P=.
同课章节目录
