2023年探究中考数学最值之瓜豆原理(无答案)
文档属性
| 名称 | 2023年探究中考数学最值之瓜豆原理(无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 954.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-23 10:55:21 | ||
图片预览


文档简介
2023年探究中考数学最值之瓜豆原理
瓜豆原理
必备知识
一、旋转及性质
1.旋转的定义:一个图形绕一点沿一定方向旋转一定的角度;
2.旋转三要素:①旋转中心(绕哪个点转);②旋转方向(顺时针或逆时针);③旋转角度;
3.旋转的性质:①旋转不改变图形的大小与形状,只改变图形的位置,即旋转前后图形全等;②对应点与旋转中心所连线段间的夹角等于旋转角。
二、位似及性质
1.位似的定义:若两个图形F和F'的点之间可以建立一一对应关系,并且满足:①每组对应点的连线所在的直线都经过同一点O;②每组对应点都在点O的同侧或异侧;③对每一组对应点A和A',有
(k为常数),则称图形F和F'位似,k叫位似比;
2.位似三要素:①位似中心(关于哪个点位似);②位似方向(同侧或异侧);③位似比(等于相似比);
3.位似的性质:成位似的两个图形必相似;
把一个几何图形变换成与之位似的图形,叫做位似变换;
利用位似变换可把一个图形放大或缩小,若位似比大于1,则通过位似变换把原图形放大;若位似比小于1,则通过位似变换把原图形缩小.
提炼方法
一、旋转作图
问题1:如图1,在平面内有两点A、B,请将点B绕点A按顺时针方向旋转40°.
简析:如图2所示,这里AB=AC,即“共顶点,等线段”.
图1 图2
二、位似作图
问题2:如图3,已知线段AB,请以点A为位似中心,为位似比,在同侧将线段AB进行位似变换。
图3 图4
简析如图4所示,这里,即“共顶点,定比值线段”。
三、模型建立
(一)旋转变换
问题3:(1)如图5,已知等腰Rt△APQ,其中A为定点,根据旋转作图的经验,请你说说:点Q可以看作点P经过怎样的变换得到?
(2)如图6,若改为等边ΔAPQ呢?
(3)如图7,若改为任意等腰ΔAPQ(其顶角为α)呢?
图5 图6 图7
简析:(1)点Q可以看作点P绕定点A按逆时针方向旋转90°而来;
(2)点Q可以看作点P绕定点A按逆时针方向旋转60°而来;
(3)点Q可以看作点P绕定点A按逆时针方向旋转角α而来;
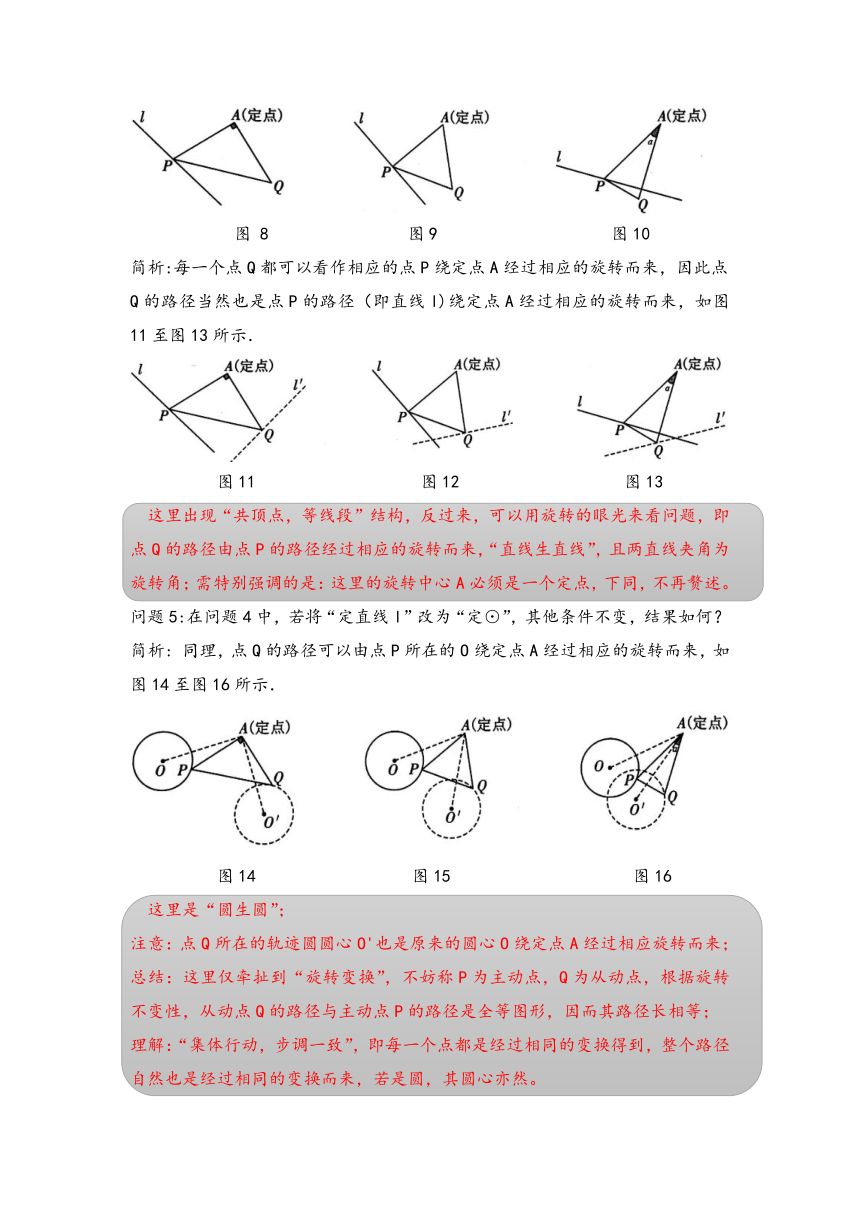
问题4:在问题3中,若点P在一条定直线l上运动,其他条件不变,如图14-2-8至图14-2-10所示,请问:点Q的运动路径是什么?它可以看作点P的路径如何而来?
图 8 图9 图10
简析:每一个点Q都可以看作相应的点P绕定点A经过相应的旋转而来,因此点Q的路径当然也是点P的路径(即直线l)绕定点A经过相应的旋转而来,如图11至图13所示.
图11 图12 图13
这里出现“共顶点,等线段”结构,反过来,可以用旋转的眼光来看问题,即点Q的路径由点P的路径经过相应的旋转而来,“直线生直线”,且两直线夹角为旋转角;需特别强调的是:这里的旋转中心A必须是一个定点,下同,不再赘述。
问题5:在问题4中,若将“定直线l”改为“定⊙”,其他条件不变,结果如何?
简析: 同理,点Q的路径可以由点P所在的O绕定点A经过相应的旋转而来,如图14至图16所示.
图14 图15 图16
这里是“圆生圆”;
注意:点Q所在的轨迹圆圆心O'也是原来的圆心O绕定点A经过相应旋转而来;
总结:这里仅牵扯到“旋转变换”,不妨称P为主动点,Q为从动点,根据旋转不变性,从动点Q的路径与主动点P的路径是全等图形,因而其路径长相等;
理解:“集体行动,步调一致”,即每一个点都是经过相同的变换得到,整个路径自然也是经过相同的变换而来,若是圆,其圆心亦然。
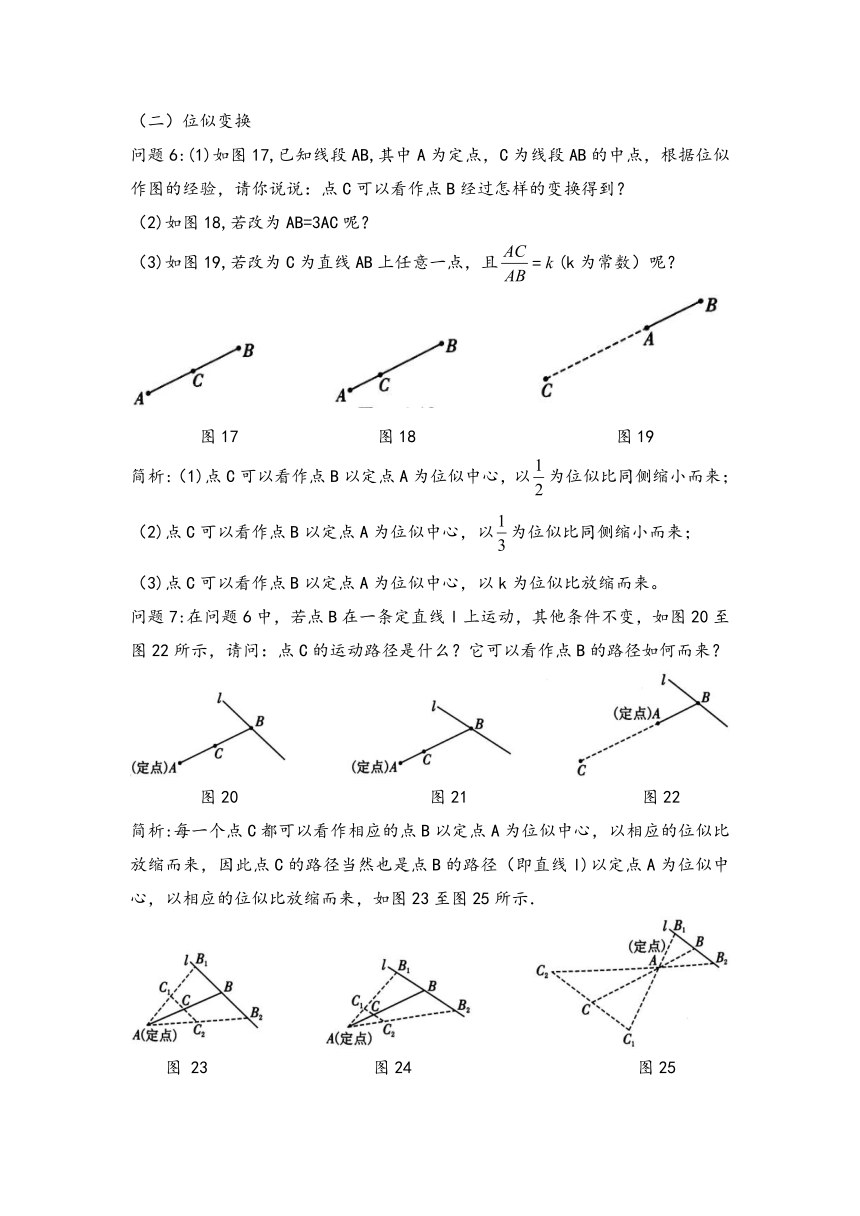
(二)位似变换
问题6:(1)如图17,已知线段AB,其中A为定点,C为线段AB的中点,根据位似作图的经验,请你说说:点C可以看作点B经过怎样的变换得到?
(2)如图18,若改为AB=3AC呢?
(3)如图19,若改为C为直线AB上任意一点,且(k为常数)呢?
图17 图18 图19
简析:(1)点C可以看作点B以定点A为位似中心,以为位似比同侧缩小而来;
(2)点C可以看作点B以定点A为位似中心,以为位似比同侧缩小而来;
(3)点C可以看作点B以定点A为位似中心,以k为位似比放缩而来。
问题7:在问题6中,若点B在一条定直线l上运动,其他条件不变,如图20至图22所示,请问:点C的运动路径是什么?它可以看作点B的路径如何而来?
图20 图21 图22
简析:每一个点C都可以看作相应的点B以定点A为位似中心,以相应的位似比放缩而来,因此点C的路径当然也是点B的路径(即直线l)以定点A为位似中心,以相应的位似比放缩而来,如图23至图25所示.
图 23 图24 图25
这里出现“共顶点,定比值线段”结构,反过来,可以用位似的眼光来看问题,即点C的路径由点B的路径经过相应的位似变换而来,“直线依然生直线”;
值得一提的是,因为“两点确定一条直线”,故只要作两个(特殊)点的位似变换即可。
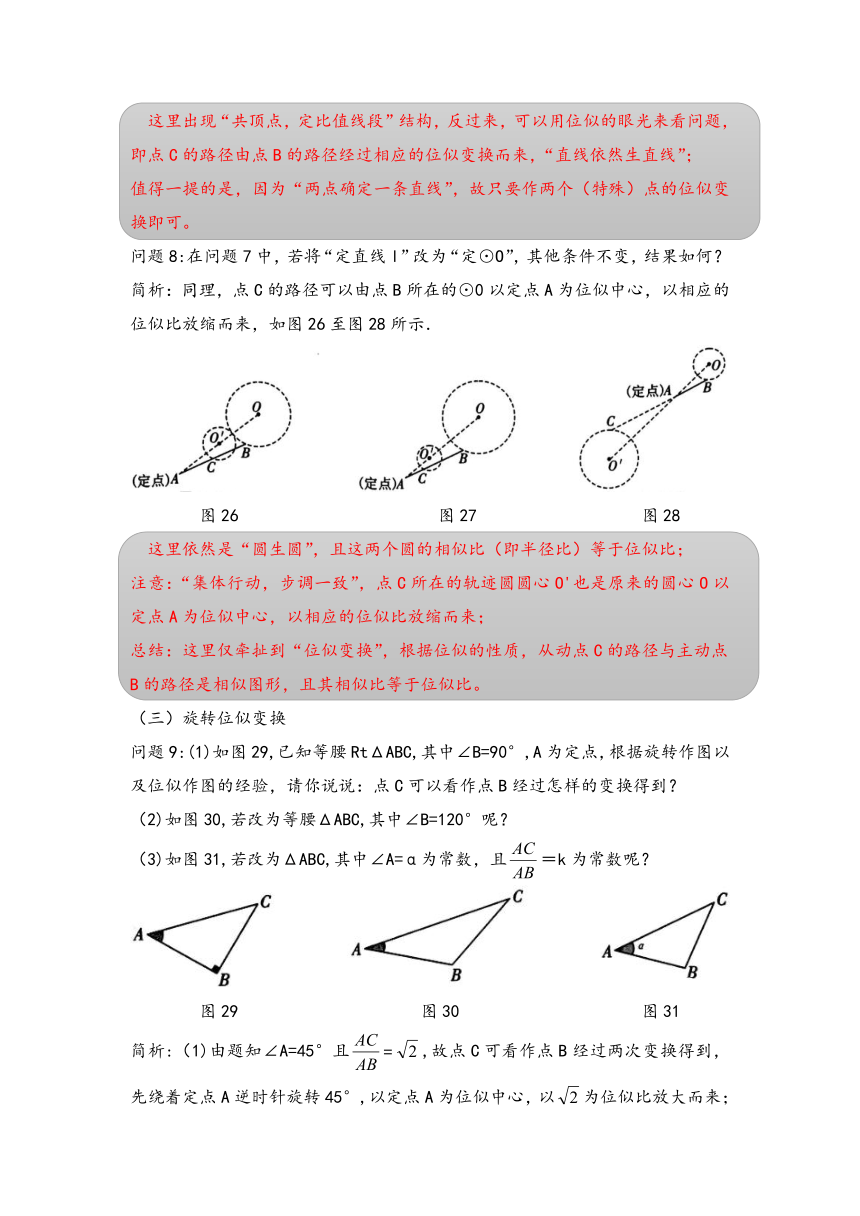
问题8:在问题7中,若将“定直线l”改为“定⊙O”,其他条件不变,结果如何?
简析:同理,点C的路径可以由点B所在的⊙0以定点A为位似中心,以相应的位似比放缩而来,如图26至图28所示.
图26 图27 图28
这里依然是“圆生圆”,且这两个圆的相似比(即半径比)等于位似比;
注意:“集体行动,步调一致”,点C所在的轨迹圆圆心O'也是原来的圆心O以定点A为位似中心,以相应的位似比放缩而来;
总结:这里仅牵扯到“位似变换”,根据位似的性质,从动点C的路径与主动点B的路径是相似图形,且其相似比等于位似比。
(三)旋转位似变换
问题9:(1)如图29,已知等腰RtΔABC,其中∠B=90°,A为定点,根据旋转作图以及位似作图的经验,请你说说:点C可以看作点B经过怎样的变换得到?
(2)如图30,若改为等腰ΔABC,其中∠B=120°呢?
(3)如图31,若改为ΔABC,其中∠A=α为常数,且=k为常数呢?
图29 图30 图31
简析:(1)由题知∠A=45°且,故点C可看作点B经过两次变换得到,先绕着定点A逆时针旋转45°,以定点A为位似中心,以为位似比放大而来;
(2)同理,由∠A=30°且,可知点C可以看作点B先绕着定点A逆时针旋转30°,再以定点A为位似中心,以为位似比放大而来;
(3)更一般地,点C可以看作点B先绕着定点A逆时针旋转角α,再以定点A为位似中心,以k为位似比放缩而来。
问题10:在问题9中,若点B在一条定直线l上运动,其他条件不变,如图32至图34所示,请问:点C的运动路径是什么?它可以看作点B的路径如何而来?
图32 图33 图34
简析:每一个点C都可以看作相应的点B先旋转后位似而来,因此点C的路径当然也是点B的路径(即直线l)先旋转后位似而来,如图35至图37所示.
图35 图36 图37
这里出现“共顶点,定夹角,定比值线段”结构,反过来,可以用旋转加位似的眼光看问题,即点C的路径由点B的路径经过相应的旋转位似变换而来,“直线还是生直线”。
问题11:在问题10中,将“定直线l”改为“定⊙O”,其他条件不变,结果如何?
简析:同理,点C的路径可以由点B所在的O先旋转后位似而来,如图38至图40所示.
图38 图39 图40
这里还是“圆生圆”,且这两个圆的相似比(即半径比)等于位似比;
注意:“集体行动,步调一致”,点C所在的轨迹圆圆心O也是原来的圆心O先旋转后位似而来;
总结:这里既牵扯“旋转变换”,又涉及“位似变换”,故称“旋转位似变换”;
根据旋转不变性以及位似的性质,从动点C的路径与主动点B的路径依然是相似图形,且其相似比等于位似比。
四、具体案例
(1)如图41,已知AB=2,点D是等腰RtΔABC斜边AC上一动点,以BD为一边向右下方作等边ΔBDE,当点D由点A运动到点C时,求点E运动的路径长;
(2)如图42,已知AB=2,点D是等腰RtΔABC斜边AC上一动点,以BD为斜边向右下方作等腰RtΔBDE,当点D由点A运动到点C时,求点E运动的路径长;
图41 图42 图43 图44
(3)如图43,已知AB=2,点D是等腰RtΔABC斜边AC上一动点,以BD为一边向右下方作以点D为直角顶点的等腰RtΔBDE,当点D由点A运动到点C时,求点E运动的路径长;
(4)如图44,已知AB=2,点D是等腰RtΔABC斜边AC上一动点,以BD为一边向右下方作等腰ΔBDE,其顶角∠BDE=120°,当点D由点A运动到点C时,求点E运动的路径长.
简析(1)点B为定点,从动点E可以看作主动点D绕点B顺时针旋转60°而来,故点E运动的路径长等于点D运动的路径长,即为2;
(2)点B为定点,从动点E可以看作主动点D先绕点B顺时针旋转45°,再以点B为位似中心,以为位似比缩小而来,故点E运动的路径长等于点D运动路径长的,即为2;
(3)点B为定点,从动点E可以看作主动点D先绕点B顺时针旋转45°,再以点B为位似中心,以为位似比放大而来,故点E运动的路径长等于点D运动路径长的倍,即为4;
(4)同理,点E运动的路径长等于点D运动路径长的倍,即为2.
五、总结反思
1.图形变换(平移、翻折、旋转及位似等)的本质是点变换;反过来,点变换也可以看作该点所在图形的变换,这是整体与局部之间辩证统一的关系;
2.分析问题时,要做到眼中有“点”:先找定点,再确定从动点如何随着主动点的运动而运动,即主动点关于定点经过怎样的变换可以得到从动点;
3.“直线(段)生直线(段)”、“圆(弧)生圆(弧)”、“折线(段)生折线(段)”、“抛物线生抛物线”、“双曲线生双曲线”等,真可谓“种瓜得瓜,种豆得豆”,不妨称为“瓜豆原理”;
4.“瓜豆原理”的本质是作图原理的逆过程;
5.特别强调:使用“瓜豆原理”的前提是必须存在定点来充当旋转(位似)中心,使主动点经过相应的变换可以得到从动点,即“无定点,不瓜豆”。
实战分折
(一)求路径长
例1(2016年湖北武汉)如图45,在等腰RtΔABC中,AC=BC=2,点P在以
斜边AB为直径的半圆上,M为PC的中点。当点P沿半圆从点A运动至点B时,则点M运动的路径长是( )
图45
A.π B.π C.2 D.2
简析:C为定点,点M随着点P的运动而运动,由M为PC的中点,可得
用位似变换的眼光来看,点M可以看作点P以定点C为位似中心,以为位似比缩小而来,故点M运动的路径也是点P运动的路径相应而来,即点M的路径长等于点P路径长的,因此点M运动的路径长是π,选B.
这里只涉及“位似变换”,其常规解法是利用定义法说明“圆弧型”路径。
例2(2013年浙江湖州)如图46,已知点A是第一象限内横坐标为2的一个定点,AN⊥x轴于点M,交直线y=-x于点N.若点P是线段ON上的一个动点,∠APB=30°,BA⊥PA,点P在线段ON上运动时,A点不变,B点随之运动。求当点P从点O运动到点N时,点B运动的路径长。
图46
简析:A为定点,点B随着点P的运动而运动,由题知∠PAB=90°,且;
用旋转位似变换的眼光来看,点B可以看作点P先绕定点A逆时针旋转90°,再以定点A为位似中心,以为位似比缩小而来,故点B运动的路径也是由点P运动的路径相应而来,即点B的路径长等于点P路径长的,因此点B运动的路径长是2.
这里属“旋转位似变换”,其常规解法是利用夹角定位法说明“直线型”路径。
例3 如图47,已知扇形AOB中,OA=3,∠AOB=120°.C是AB上的动点,以BC为边向右上方作正方形BCDE.当点C从点A移动至点B时,求点D经过的路径长。
图47 图 48
简析:如图48,连接BD,ΔBCD为等腰直角三角形,则∠CBD=45°,且
B为定点,点D随着点C的运动而运动;
用旋转位似变换的眼光来看,点D可以看作点C先绕定点B顺时针旋转45°,再以定点B为位似中心,以为位似比放大而来,故点D运动的路径也是由点C运动的路径相应而来,即点D的路径长等于点C路径长的倍,因此点D经过的路径长是2π.
这里属“旋转位似变换”;若求点E经过的路径长,可以锁定等腰RtΔCBE,得知点E的路径长等于点C的路径长,这时只涉及“旋转变换”。
总结:使用“瓜豆原理”的关键是主动寻找“瓜豆三点”:定点、主动点、从动点;一般情况下,主、从动点比较简单,但定点的选择尤为重要,用常见图形变换的眼光(如旋转、位似变换等)看这三个点之间的关联,即主动点关于定点如何变换可以得到从动点,那么其相应的路径也可以如此变换而来;
需要特别谨记的是“无定点,不瓜豆”,即若找不到一个定点充当主动点与从动点之间的桥梁(旋转中心或位似中心等),一般情况下,“瓜豆”就成了“无源之水、无本之木”,不可能再“生根发芽”了;
请记住,没有绝对的通法,所谓通法也仅仅是很大范围内适用的解法罢了;因为旋转不改变图形的大小与形状,故不影响路径长;而位似变换影响路径长,且从动点的路径长是主动点的路径长乘以相应的位似比;
(二)求最值
例4(2017年江苏徐州)如图49,已知二次函数的图像与x轴交于A、B两点,与y轴交于点C,⊙C的半径为,P为⊙C上一动点,连接PB,若E为PB的中点,连接OE,则OE的最大值为_______.
图49
简析:如图49,由E为PB的中点,可得,B为定点,P为主动点,E为从动点;从动点E可以看作主动点P以定点B为位似中心,以为位似比缩小而来,故从动点E的路径也是主动点P的路径(即⊙C)以定点B为位似中心,以
为位似比缩小而来;
特别是,圆心也是如此而来,即连接BC,取其中点M即为从动点E的轨迹圆圆心,且其半径ME为,因此OE的最大值为OM+ME=BC+ME=
“瓜豆原理”可以秒杀相关的路径长问题,但若涉及最值问题,则必须将目标动点的路径作出来,然后转化为“点圆距离”或“点线距离”等问题;
此题若不使用“瓜豆原理”,可以利用中点的常见处理策略解决,参见下一题:
例5如图50,在等边ΔABC中,AB=2,点D是以A为圆心,半径为1的圆上一动点,连接CD,E为CD的中点,连接BE,则BE的最大值与最小值之和为________.
图50 图51 图52 图53
简析1:如图51,取AC的中点F,连接EF、BF、AD,易得BF=AB=,EF
=AD=,在ΔBEF中,有BF-EF≤BE≤BF+EF,即-≤BE≤+,当且仅当B、E、F三点共线时取等,故BE的最小值为-,最大值为+,其和为2.
简析2:如图52,延长CB至点F,使BF=CB,连接DF,则BE为ΔCDF的中位线,故BE=FD;要求BE的最值,转化求FD的最值,这是一个典型的“点圆距离”问题,其最小值为FA-AD=FA-1,最大值为FA+AD=FA+1;
又∠FAC=90°,FA=2,故FD最小值为2-1,最大值为2+1,下略.
这两种方法属典型的中点处理策略,即构造中位线模型,法1通过取中点,法2通过倍长的方式,尤其是法2的转化异常精彩,没有转化,就没有数学。
简析3:如图53,由E为CD的中点,结合“瓜豆原理”,可知点E的路径是一个圆,且由⊙A以定点C为位似中心,以为位似比缩小而来,其圆心亦然,即为图中的⊙F,其中点F为AC的中点,则BE的最值问题转化为“点圆距离”问题,下略。
法3采取了“瓜豆原理”,其实这三种方法的本质相同,前两种中点处理策略告诉我们“是什么”,“瓜豆法”告诉我们“为什么”,即为什么取AC的中点F.
★★★总结:使用“瓜豆原理”解题的基本步骤为:
1.主动寻找“瓜豆三点”:定点、主动点、从动点(无定点,不瓜豆);
2.用常见的图形变化(如平移、翻折、旋转及位似等)眼光看待“瓜豆三点”,即从动点可以看成是主动点关于定点如何变幻而来;
3.从动点路径与主动点路径之间的变幻关系,完全等同于点的变幻关系;
4.若问路径长,可口算;若问最值,需作图,转化为“点圆距离”或“点线距离”
【瓜豆原理练习】
1、如图,正方形ABCD的边长为4,E为BC上一点,且BE=1,F为AB边上的一个动点,连接EF,以EF为边向右侧作等边△EFG,连接CG,则CG的最小值为 .
第1题图 第2题图 第3题图
2、如图,等腰Rt△ABC中,斜边AB的长为2,O为AB的中点,P为AC边上的动点,OQ⊥OP交BC于点Q,M为PQ的中点,当点P从点A运动到点C时,点M所经过的路线长为( )
A. B. C.1 D.2
3、如图,等边三角形ABC的边长为4,点D是直线AB上一点.将线段CD绕点D顺时针旋转60°得到线段DE,连结BE.
(1)若点D在AB边上(不与A,B重合)请依题意补全图并证明AD=BE;
(2)连接AE,当AE的长最小时,求CD的长.
4.如图,在△ABC中,∠ACB=90°,∠A=30°,BC=2,D是AB上一动点,以DC为斜边向右侧作等腰Rt△DCE,使得∠CED=90°,连接BE,则线段BE的最小值为_______.
5.(高新6模 将军饮马+瓜豆原理)如图,矩形ABCD中,AB=6,BC=10,点E是AD边上的中点,点F是线段AB上任意一点,连接EF,以EF为边在AD下方作等腰直角ΔEFG,连接DG,则ΔDEG周长最小值为_______.
6.(铁一中4模 瓜豆原理+将军饮马)如图,在平面直角坐标系中,A(-1,0),B(0,2),C为x轴上一个动点,以BC为一边作等腰RtΔBCD,使得∠BCD=90°,CB=CD,连接AD,则AD+BD的最小值为________.
7.(铁一中5模 瓜豆原理)如图,在正方形ABCD中,E是对角线AC上一动点,以DE为边作正方形DEFG,H是CD中点,连接GH,若GH的最小值是1,则正方形ABCD的边长为_______.
8.(交大附中3模 瓜豆原理+手拉手模型+旋转)如图,在RtΔABC中,∠ACB=90°,AB=4,以AC为边在ΔABC外作等边ΔACD,连接BD,则BD的最大值
为______.
9.(师大附中8模 瓜豆原理)如图,矩形ABCD中,AB=10,AD=5,E为AB的中点,F为EC上一动点,P为DF中点,连接PB,则PB的最小值为______.
如图,在平面直角坐标系中,A(-3,0),点B是y轴正半轴上一动点,以AB为边在AB的下方作等边△ABP,点B在y轴上运动时,求OP的最小值.
11.如图,点A(-1,0),B(0,-1),作点A关于y轴的对称点C,若点P是直线AB 上的动点,连CP,将CP绕点C逆时针旋转90°至CQ,则OQ+AQ的最小值是 .
瓜豆原理
必备知识
一、旋转及性质
1.旋转的定义:一个图形绕一点沿一定方向旋转一定的角度;
2.旋转三要素:①旋转中心(绕哪个点转);②旋转方向(顺时针或逆时针);③旋转角度;
3.旋转的性质:①旋转不改变图形的大小与形状,只改变图形的位置,即旋转前后图形全等;②对应点与旋转中心所连线段间的夹角等于旋转角。
二、位似及性质
1.位似的定义:若两个图形F和F'的点之间可以建立一一对应关系,并且满足:①每组对应点的连线所在的直线都经过同一点O;②每组对应点都在点O的同侧或异侧;③对每一组对应点A和A',有
(k为常数),则称图形F和F'位似,k叫位似比;
2.位似三要素:①位似中心(关于哪个点位似);②位似方向(同侧或异侧);③位似比(等于相似比);
3.位似的性质:成位似的两个图形必相似;
把一个几何图形变换成与之位似的图形,叫做位似变换;
利用位似变换可把一个图形放大或缩小,若位似比大于1,则通过位似变换把原图形放大;若位似比小于1,则通过位似变换把原图形缩小.
提炼方法
一、旋转作图
问题1:如图1,在平面内有两点A、B,请将点B绕点A按顺时针方向旋转40°.
简析:如图2所示,这里AB=AC,即“共顶点,等线段”.
图1 图2
二、位似作图
问题2:如图3,已知线段AB,请以点A为位似中心,为位似比,在同侧将线段AB进行位似变换。
图3 图4
简析如图4所示,这里,即“共顶点,定比值线段”。
三、模型建立
(一)旋转变换
问题3:(1)如图5,已知等腰Rt△APQ,其中A为定点,根据旋转作图的经验,请你说说:点Q可以看作点P经过怎样的变换得到?
(2)如图6,若改为等边ΔAPQ呢?
(3)如图7,若改为任意等腰ΔAPQ(其顶角为α)呢?
图5 图6 图7
简析:(1)点Q可以看作点P绕定点A按逆时针方向旋转90°而来;
(2)点Q可以看作点P绕定点A按逆时针方向旋转60°而来;
(3)点Q可以看作点P绕定点A按逆时针方向旋转角α而来;
问题4:在问题3中,若点P在一条定直线l上运动,其他条件不变,如图14-2-8至图14-2-10所示,请问:点Q的运动路径是什么?它可以看作点P的路径如何而来?
图 8 图9 图10
简析:每一个点Q都可以看作相应的点P绕定点A经过相应的旋转而来,因此点Q的路径当然也是点P的路径(即直线l)绕定点A经过相应的旋转而来,如图11至图13所示.
图11 图12 图13
这里出现“共顶点,等线段”结构,反过来,可以用旋转的眼光来看问题,即点Q的路径由点P的路径经过相应的旋转而来,“直线生直线”,且两直线夹角为旋转角;需特别强调的是:这里的旋转中心A必须是一个定点,下同,不再赘述。
问题5:在问题4中,若将“定直线l”改为“定⊙”,其他条件不变,结果如何?
简析: 同理,点Q的路径可以由点P所在的O绕定点A经过相应的旋转而来,如图14至图16所示.
图14 图15 图16
这里是“圆生圆”;
注意:点Q所在的轨迹圆圆心O'也是原来的圆心O绕定点A经过相应旋转而来;
总结:这里仅牵扯到“旋转变换”,不妨称P为主动点,Q为从动点,根据旋转不变性,从动点Q的路径与主动点P的路径是全等图形,因而其路径长相等;
理解:“集体行动,步调一致”,即每一个点都是经过相同的变换得到,整个路径自然也是经过相同的变换而来,若是圆,其圆心亦然。
(二)位似变换
问题6:(1)如图17,已知线段AB,其中A为定点,C为线段AB的中点,根据位似作图的经验,请你说说:点C可以看作点B经过怎样的变换得到?
(2)如图18,若改为AB=3AC呢?
(3)如图19,若改为C为直线AB上任意一点,且(k为常数)呢?
图17 图18 图19
简析:(1)点C可以看作点B以定点A为位似中心,以为位似比同侧缩小而来;
(2)点C可以看作点B以定点A为位似中心,以为位似比同侧缩小而来;
(3)点C可以看作点B以定点A为位似中心,以k为位似比放缩而来。
问题7:在问题6中,若点B在一条定直线l上运动,其他条件不变,如图20至图22所示,请问:点C的运动路径是什么?它可以看作点B的路径如何而来?
图20 图21 图22
简析:每一个点C都可以看作相应的点B以定点A为位似中心,以相应的位似比放缩而来,因此点C的路径当然也是点B的路径(即直线l)以定点A为位似中心,以相应的位似比放缩而来,如图23至图25所示.
图 23 图24 图25
这里出现“共顶点,定比值线段”结构,反过来,可以用位似的眼光来看问题,即点C的路径由点B的路径经过相应的位似变换而来,“直线依然生直线”;
值得一提的是,因为“两点确定一条直线”,故只要作两个(特殊)点的位似变换即可。
问题8:在问题7中,若将“定直线l”改为“定⊙O”,其他条件不变,结果如何?
简析:同理,点C的路径可以由点B所在的⊙0以定点A为位似中心,以相应的位似比放缩而来,如图26至图28所示.
图26 图27 图28
这里依然是“圆生圆”,且这两个圆的相似比(即半径比)等于位似比;
注意:“集体行动,步调一致”,点C所在的轨迹圆圆心O'也是原来的圆心O以定点A为位似中心,以相应的位似比放缩而来;
总结:这里仅牵扯到“位似变换”,根据位似的性质,从动点C的路径与主动点B的路径是相似图形,且其相似比等于位似比。
(三)旋转位似变换
问题9:(1)如图29,已知等腰RtΔABC,其中∠B=90°,A为定点,根据旋转作图以及位似作图的经验,请你说说:点C可以看作点B经过怎样的变换得到?
(2)如图30,若改为等腰ΔABC,其中∠B=120°呢?
(3)如图31,若改为ΔABC,其中∠A=α为常数,且=k为常数呢?
图29 图30 图31
简析:(1)由题知∠A=45°且,故点C可看作点B经过两次变换得到,先绕着定点A逆时针旋转45°,以定点A为位似中心,以为位似比放大而来;
(2)同理,由∠A=30°且,可知点C可以看作点B先绕着定点A逆时针旋转30°,再以定点A为位似中心,以为位似比放大而来;
(3)更一般地,点C可以看作点B先绕着定点A逆时针旋转角α,再以定点A为位似中心,以k为位似比放缩而来。
问题10:在问题9中,若点B在一条定直线l上运动,其他条件不变,如图32至图34所示,请问:点C的运动路径是什么?它可以看作点B的路径如何而来?
图32 图33 图34
简析:每一个点C都可以看作相应的点B先旋转后位似而来,因此点C的路径当然也是点B的路径(即直线l)先旋转后位似而来,如图35至图37所示.
图35 图36 图37
这里出现“共顶点,定夹角,定比值线段”结构,反过来,可以用旋转加位似的眼光看问题,即点C的路径由点B的路径经过相应的旋转位似变换而来,“直线还是生直线”。
问题11:在问题10中,将“定直线l”改为“定⊙O”,其他条件不变,结果如何?
简析:同理,点C的路径可以由点B所在的O先旋转后位似而来,如图38至图40所示.
图38 图39 图40
这里还是“圆生圆”,且这两个圆的相似比(即半径比)等于位似比;
注意:“集体行动,步调一致”,点C所在的轨迹圆圆心O也是原来的圆心O先旋转后位似而来;
总结:这里既牵扯“旋转变换”,又涉及“位似变换”,故称“旋转位似变换”;
根据旋转不变性以及位似的性质,从动点C的路径与主动点B的路径依然是相似图形,且其相似比等于位似比。
四、具体案例
(1)如图41,已知AB=2,点D是等腰RtΔABC斜边AC上一动点,以BD为一边向右下方作等边ΔBDE,当点D由点A运动到点C时,求点E运动的路径长;
(2)如图42,已知AB=2,点D是等腰RtΔABC斜边AC上一动点,以BD为斜边向右下方作等腰RtΔBDE,当点D由点A运动到点C时,求点E运动的路径长;
图41 图42 图43 图44
(3)如图43,已知AB=2,点D是等腰RtΔABC斜边AC上一动点,以BD为一边向右下方作以点D为直角顶点的等腰RtΔBDE,当点D由点A运动到点C时,求点E运动的路径长;
(4)如图44,已知AB=2,点D是等腰RtΔABC斜边AC上一动点,以BD为一边向右下方作等腰ΔBDE,其顶角∠BDE=120°,当点D由点A运动到点C时,求点E运动的路径长.
简析(1)点B为定点,从动点E可以看作主动点D绕点B顺时针旋转60°而来,故点E运动的路径长等于点D运动的路径长,即为2;
(2)点B为定点,从动点E可以看作主动点D先绕点B顺时针旋转45°,再以点B为位似中心,以为位似比缩小而来,故点E运动的路径长等于点D运动路径长的,即为2;
(3)点B为定点,从动点E可以看作主动点D先绕点B顺时针旋转45°,再以点B为位似中心,以为位似比放大而来,故点E运动的路径长等于点D运动路径长的倍,即为4;
(4)同理,点E运动的路径长等于点D运动路径长的倍,即为2.
五、总结反思
1.图形变换(平移、翻折、旋转及位似等)的本质是点变换;反过来,点变换也可以看作该点所在图形的变换,这是整体与局部之间辩证统一的关系;
2.分析问题时,要做到眼中有“点”:先找定点,再确定从动点如何随着主动点的运动而运动,即主动点关于定点经过怎样的变换可以得到从动点;
3.“直线(段)生直线(段)”、“圆(弧)生圆(弧)”、“折线(段)生折线(段)”、“抛物线生抛物线”、“双曲线生双曲线”等,真可谓“种瓜得瓜,种豆得豆”,不妨称为“瓜豆原理”;
4.“瓜豆原理”的本质是作图原理的逆过程;
5.特别强调:使用“瓜豆原理”的前提是必须存在定点来充当旋转(位似)中心,使主动点经过相应的变换可以得到从动点,即“无定点,不瓜豆”。
实战分折
(一)求路径长
例1(2016年湖北武汉)如图45,在等腰RtΔABC中,AC=BC=2,点P在以
斜边AB为直径的半圆上,M为PC的中点。当点P沿半圆从点A运动至点B时,则点M运动的路径长是( )
图45
A.π B.π C.2 D.2
简析:C为定点,点M随着点P的运动而运动,由M为PC的中点,可得
用位似变换的眼光来看,点M可以看作点P以定点C为位似中心,以为位似比缩小而来,故点M运动的路径也是点P运动的路径相应而来,即点M的路径长等于点P路径长的,因此点M运动的路径长是π,选B.
这里只涉及“位似变换”,其常规解法是利用定义法说明“圆弧型”路径。
例2(2013年浙江湖州)如图46,已知点A是第一象限内横坐标为2的一个定点,AN⊥x轴于点M,交直线y=-x于点N.若点P是线段ON上的一个动点,∠APB=30°,BA⊥PA,点P在线段ON上运动时,A点不变,B点随之运动。求当点P从点O运动到点N时,点B运动的路径长。
图46
简析:A为定点,点B随着点P的运动而运动,由题知∠PAB=90°,且;
用旋转位似变换的眼光来看,点B可以看作点P先绕定点A逆时针旋转90°,再以定点A为位似中心,以为位似比缩小而来,故点B运动的路径也是由点P运动的路径相应而来,即点B的路径长等于点P路径长的,因此点B运动的路径长是2.
这里属“旋转位似变换”,其常规解法是利用夹角定位法说明“直线型”路径。
例3 如图47,已知扇形AOB中,OA=3,∠AOB=120°.C是AB上的动点,以BC为边向右上方作正方形BCDE.当点C从点A移动至点B时,求点D经过的路径长。
图47 图 48
简析:如图48,连接BD,ΔBCD为等腰直角三角形,则∠CBD=45°,且
B为定点,点D随着点C的运动而运动;
用旋转位似变换的眼光来看,点D可以看作点C先绕定点B顺时针旋转45°,再以定点B为位似中心,以为位似比放大而来,故点D运动的路径也是由点C运动的路径相应而来,即点D的路径长等于点C路径长的倍,因此点D经过的路径长是2π.
这里属“旋转位似变换”;若求点E经过的路径长,可以锁定等腰RtΔCBE,得知点E的路径长等于点C的路径长,这时只涉及“旋转变换”。
总结:使用“瓜豆原理”的关键是主动寻找“瓜豆三点”:定点、主动点、从动点;一般情况下,主、从动点比较简单,但定点的选择尤为重要,用常见图形变换的眼光(如旋转、位似变换等)看这三个点之间的关联,即主动点关于定点如何变换可以得到从动点,那么其相应的路径也可以如此变换而来;
需要特别谨记的是“无定点,不瓜豆”,即若找不到一个定点充当主动点与从动点之间的桥梁(旋转中心或位似中心等),一般情况下,“瓜豆”就成了“无源之水、无本之木”,不可能再“生根发芽”了;
请记住,没有绝对的通法,所谓通法也仅仅是很大范围内适用的解法罢了;因为旋转不改变图形的大小与形状,故不影响路径长;而位似变换影响路径长,且从动点的路径长是主动点的路径长乘以相应的位似比;
(二)求最值
例4(2017年江苏徐州)如图49,已知二次函数的图像与x轴交于A、B两点,与y轴交于点C,⊙C的半径为,P为⊙C上一动点,连接PB,若E为PB的中点,连接OE,则OE的最大值为_______.
图49
简析:如图49,由E为PB的中点,可得,B为定点,P为主动点,E为从动点;从动点E可以看作主动点P以定点B为位似中心,以为位似比缩小而来,故从动点E的路径也是主动点P的路径(即⊙C)以定点B为位似中心,以
为位似比缩小而来;
特别是,圆心也是如此而来,即连接BC,取其中点M即为从动点E的轨迹圆圆心,且其半径ME为,因此OE的最大值为OM+ME=BC+ME=
“瓜豆原理”可以秒杀相关的路径长问题,但若涉及最值问题,则必须将目标动点的路径作出来,然后转化为“点圆距离”或“点线距离”等问题;
此题若不使用“瓜豆原理”,可以利用中点的常见处理策略解决,参见下一题:
例5如图50,在等边ΔABC中,AB=2,点D是以A为圆心,半径为1的圆上一动点,连接CD,E为CD的中点,连接BE,则BE的最大值与最小值之和为________.
图50 图51 图52 图53
简析1:如图51,取AC的中点F,连接EF、BF、AD,易得BF=AB=,EF
=AD=,在ΔBEF中,有BF-EF≤BE≤BF+EF,即-≤BE≤+,当且仅当B、E、F三点共线时取等,故BE的最小值为-,最大值为+,其和为2.
简析2:如图52,延长CB至点F,使BF=CB,连接DF,则BE为ΔCDF的中位线,故BE=FD;要求BE的最值,转化求FD的最值,这是一个典型的“点圆距离”问题,其最小值为FA-AD=FA-1,最大值为FA+AD=FA+1;
又∠FAC=90°,FA=2,故FD最小值为2-1,最大值为2+1,下略.
这两种方法属典型的中点处理策略,即构造中位线模型,法1通过取中点,法2通过倍长的方式,尤其是法2的转化异常精彩,没有转化,就没有数学。
简析3:如图53,由E为CD的中点,结合“瓜豆原理”,可知点E的路径是一个圆,且由⊙A以定点C为位似中心,以为位似比缩小而来,其圆心亦然,即为图中的⊙F,其中点F为AC的中点,则BE的最值问题转化为“点圆距离”问题,下略。
法3采取了“瓜豆原理”,其实这三种方法的本质相同,前两种中点处理策略告诉我们“是什么”,“瓜豆法”告诉我们“为什么”,即为什么取AC的中点F.
★★★总结:使用“瓜豆原理”解题的基本步骤为:
1.主动寻找“瓜豆三点”:定点、主动点、从动点(无定点,不瓜豆);
2.用常见的图形变化(如平移、翻折、旋转及位似等)眼光看待“瓜豆三点”,即从动点可以看成是主动点关于定点如何变幻而来;
3.从动点路径与主动点路径之间的变幻关系,完全等同于点的变幻关系;
4.若问路径长,可口算;若问最值,需作图,转化为“点圆距离”或“点线距离”
【瓜豆原理练习】
1、如图,正方形ABCD的边长为4,E为BC上一点,且BE=1,F为AB边上的一个动点,连接EF,以EF为边向右侧作等边△EFG,连接CG,则CG的最小值为 .
第1题图 第2题图 第3题图
2、如图,等腰Rt△ABC中,斜边AB的长为2,O为AB的中点,P为AC边上的动点,OQ⊥OP交BC于点Q,M为PQ的中点,当点P从点A运动到点C时,点M所经过的路线长为( )
A. B. C.1 D.2
3、如图,等边三角形ABC的边长为4,点D是直线AB上一点.将线段CD绕点D顺时针旋转60°得到线段DE,连结BE.
(1)若点D在AB边上(不与A,B重合)请依题意补全图并证明AD=BE;
(2)连接AE,当AE的长最小时,求CD的长.
4.如图,在△ABC中,∠ACB=90°,∠A=30°,BC=2,D是AB上一动点,以DC为斜边向右侧作等腰Rt△DCE,使得∠CED=90°,连接BE,则线段BE的最小值为_______.
5.(高新6模 将军饮马+瓜豆原理)如图,矩形ABCD中,AB=6,BC=10,点E是AD边上的中点,点F是线段AB上任意一点,连接EF,以EF为边在AD下方作等腰直角ΔEFG,连接DG,则ΔDEG周长最小值为_______.
6.(铁一中4模 瓜豆原理+将军饮马)如图,在平面直角坐标系中,A(-1,0),B(0,2),C为x轴上一个动点,以BC为一边作等腰RtΔBCD,使得∠BCD=90°,CB=CD,连接AD,则AD+BD的最小值为________.
7.(铁一中5模 瓜豆原理)如图,在正方形ABCD中,E是对角线AC上一动点,以DE为边作正方形DEFG,H是CD中点,连接GH,若GH的最小值是1,则正方形ABCD的边长为_______.
8.(交大附中3模 瓜豆原理+手拉手模型+旋转)如图,在RtΔABC中,∠ACB=90°,AB=4,以AC为边在ΔABC外作等边ΔACD,连接BD,则BD的最大值
为______.
9.(师大附中8模 瓜豆原理)如图,矩形ABCD中,AB=10,AD=5,E为AB的中点,F为EC上一动点,P为DF中点,连接PB,则PB的最小值为______.
如图,在平面直角坐标系中,A(-3,0),点B是y轴正半轴上一动点,以AB为边在AB的下方作等边△ABP,点B在y轴上运动时,求OP的最小值.
11.如图,点A(-1,0),B(0,-1),作点A关于y轴的对称点C,若点P是直线AB 上的动点,连CP,将CP绕点C逆时针旋转90°至CQ,则OQ+AQ的最小值是 .
同课章节目录
