人教版6下数学 3.4《圆锥的认识》同步练习(含答案)
文档属性
| 名称 | 人教版6下数学 3.4《圆锥的认识》同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 132.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-23 00:00:00 | ||
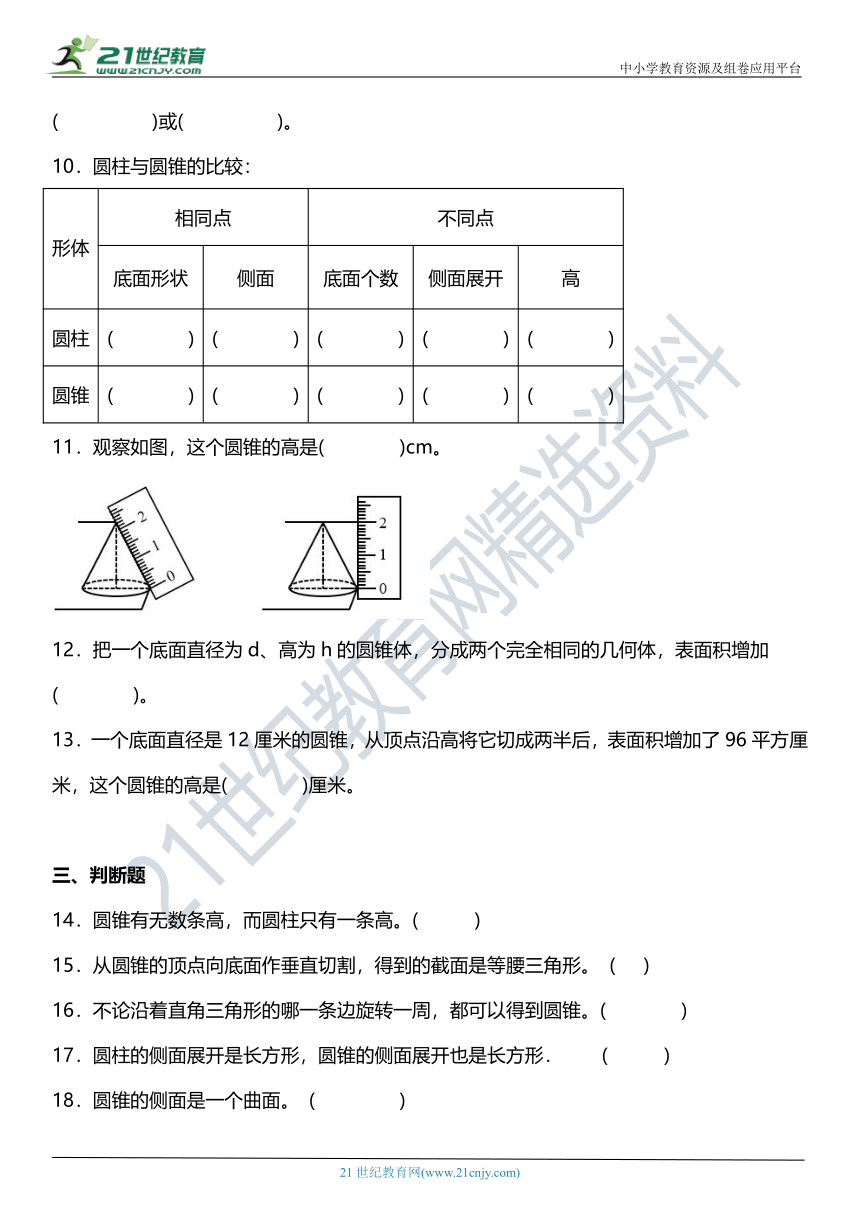
图片预览


文档简介
中小学教育资源及组卷应用平台
3.4《圆锥的认识》同步练习
班级:_________ 姓名:__________
一、选择题
1.直角三角形ABC(如下图),以直角边AB为轴旋转360°后得到的是( )。
A.底面半径是8cm,高是6cm的圆锥
B.底面半径是6cm,高是8cm的圆锥
C.底面直径是6cm,高是8cm的圆锥
2.以下能准确测量圆锥高的方法是( )。
A. B. C. D.
3.小华从正面看一个几何体,所看到的的形状是正方形,这个几何体不可能是( )。
A.长方体 B.正方体 C.圆柱 D.圆锥
4.如图所示,把一张三条边长分别是5cm、12cm和13cm的直角三角形硬纸贴在木棒上,快速转动木棒,转出的圆锥高是( )cm,底面半径是( )cm。
A.5,12 B.12,5 C.13,5 D.12,13
5.将一个圆锥沿高切成两部分,切面是( )。
A.扇形 B.等边三角形 C.等腰三角形 D.长方形
二、填空题
6.圆锥的底面是一个________,侧面是一个________,从圆锥的________到底面圆心的距离是圆锥的________,圆锥有________条高.
7.把一个圆锥沿着高切开,得到两个如图所示的物体,截面的面积和是10cm2。如果原来圆锥的高是5cm,它的底面半径是( )cm,底面积是( )cm2。
8.下面的物体形状是圆柱的画“○”,是圆锥的画“☆”。
( ) ( ) ( ) ( )
( ) ( ) ( ) ( )
9.一个直角三角形的两条直角边分别为3厘米,4厘米,以其中的一条直角边为轴旋转一周,可得到一个( ),这个图形的底面周长是( )或( );高是( )或( )。
10.圆柱与圆锥的比较:
形体 相同点 不同点
底面形状 侧面 底面个数 侧面展开 高
圆柱 ( ) ( ) ( ) ( ) ( )
圆锥 ( ) ( ) ( ) ( ) ( )
11.观察如图,这个圆锥的高是( )cm。
12.把一个底面直径为d、高为h的圆锥体,分成两个完全相同的几何体,表面积增加( )。
13.一个底面直径是12厘米的圆锥,从顶点沿高将它切成两半后,表面积增加了96平方厘米,这个圆锥的高是( )厘米。
三、判断题
14.圆锥有无数条高,而圆柱只有一条高。( )
15.从圆锥的顶点向底面作垂直切割,得到的截面是等腰三角形。 ( )
16.不论沿着直角三角形的哪一条边旋转一周,都可以得到圆锥。( )
17.圆柱的侧面展开是长方形,圆锥的侧面展开也是长方形. ( )
18.圆锥的侧面是一个曲面。 ( )
四、解答题
19.如图,有一个圆锥形沙堆的底面直径BC为4厘米,圆锥的侧面展开圆心角为120度,母线AC的长度为6厘米.请问:
(1)如果一只蚂蚁想从B点去C点,最短路线应该怎么走?请设计出一条最短路线(蚂蚁只能在圆锥表面走);
(2)如果一只蚂蚁需要由B点出发到达线段AC上(可以到其上的任意一点),那么最短路线应该怎么走?
20.将一个底面直径是、高是的圆锥形木块分成形状、大小完全相同的两个木块后,表面积比原来增加了多少平方厘米?
21.一个直角三角形两条直角边的长分别是4cm和3cm,如果以一条直角边为轴旋转一周会得到一个圆锥.怎样旋转得到的圆锥的底面积最大?最大是多少?
参考答案:
1.B
2.D
3.D
4.B
5.C
6. 圆 曲面 顶点 高 1
7. 1 3.14
8.(☆) ( ) (☆) (☆)
( ) (○) ( ) ( )
9. 圆锥 18.84厘米 25.12厘米 4厘米 3厘米
10. 圆 曲面 2 长方形 无数条 圆 曲面 1 扇形 1
11.2
12.dh
13.8
14.×
15.√
16.×
17.×
18.√
19.(1)B′C即为最短路线.(2)线段B′D即为最短路线.解答作图如下:
20.
21.以长是3cm的直角边为轴进行旋转,得到的圆锥的底面积最大 3.14×42=50.24(cm2)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
3.4《圆锥的认识》同步练习
班级:_________ 姓名:__________
一、选择题
1.直角三角形ABC(如下图),以直角边AB为轴旋转360°后得到的是( )。
A.底面半径是8cm,高是6cm的圆锥
B.底面半径是6cm,高是8cm的圆锥
C.底面直径是6cm,高是8cm的圆锥
2.以下能准确测量圆锥高的方法是( )。
A. B. C. D.
3.小华从正面看一个几何体,所看到的的形状是正方形,这个几何体不可能是( )。
A.长方体 B.正方体 C.圆柱 D.圆锥
4.如图所示,把一张三条边长分别是5cm、12cm和13cm的直角三角形硬纸贴在木棒上,快速转动木棒,转出的圆锥高是( )cm,底面半径是( )cm。
A.5,12 B.12,5 C.13,5 D.12,13
5.将一个圆锥沿高切成两部分,切面是( )。
A.扇形 B.等边三角形 C.等腰三角形 D.长方形
二、填空题
6.圆锥的底面是一个________,侧面是一个________,从圆锥的________到底面圆心的距离是圆锥的________,圆锥有________条高.
7.把一个圆锥沿着高切开,得到两个如图所示的物体,截面的面积和是10cm2。如果原来圆锥的高是5cm,它的底面半径是( )cm,底面积是( )cm2。
8.下面的物体形状是圆柱的画“○”,是圆锥的画“☆”。
( ) ( ) ( ) ( )
( ) ( ) ( ) ( )
9.一个直角三角形的两条直角边分别为3厘米,4厘米,以其中的一条直角边为轴旋转一周,可得到一个( ),这个图形的底面周长是( )或( );高是( )或( )。
10.圆柱与圆锥的比较:
形体 相同点 不同点
底面形状 侧面 底面个数 侧面展开 高
圆柱 ( ) ( ) ( ) ( ) ( )
圆锥 ( ) ( ) ( ) ( ) ( )
11.观察如图,这个圆锥的高是( )cm。
12.把一个底面直径为d、高为h的圆锥体,分成两个完全相同的几何体,表面积增加( )。
13.一个底面直径是12厘米的圆锥,从顶点沿高将它切成两半后,表面积增加了96平方厘米,这个圆锥的高是( )厘米。
三、判断题
14.圆锥有无数条高,而圆柱只有一条高。( )
15.从圆锥的顶点向底面作垂直切割,得到的截面是等腰三角形。 ( )
16.不论沿着直角三角形的哪一条边旋转一周,都可以得到圆锥。( )
17.圆柱的侧面展开是长方形,圆锥的侧面展开也是长方形. ( )
18.圆锥的侧面是一个曲面。 ( )
四、解答题
19.如图,有一个圆锥形沙堆的底面直径BC为4厘米,圆锥的侧面展开圆心角为120度,母线AC的长度为6厘米.请问:
(1)如果一只蚂蚁想从B点去C点,最短路线应该怎么走?请设计出一条最短路线(蚂蚁只能在圆锥表面走);
(2)如果一只蚂蚁需要由B点出发到达线段AC上(可以到其上的任意一点),那么最短路线应该怎么走?
20.将一个底面直径是、高是的圆锥形木块分成形状、大小完全相同的两个木块后,表面积比原来增加了多少平方厘米?
21.一个直角三角形两条直角边的长分别是4cm和3cm,如果以一条直角边为轴旋转一周会得到一个圆锥.怎样旋转得到的圆锥的底面积最大?最大是多少?
参考答案:
1.B
2.D
3.D
4.B
5.C
6. 圆 曲面 顶点 高 1
7. 1 3.14
8.(☆) ( ) (☆) (☆)
( ) (○) ( ) ( )
9. 圆锥 18.84厘米 25.12厘米 4厘米 3厘米
10. 圆 曲面 2 长方形 无数条 圆 曲面 1 扇形 1
11.2
12.dh
13.8
14.×
15.√
16.×
17.×
18.√
19.(1)B′C即为最短路线.(2)线段B′D即为最短路线.解答作图如下:
20.
21.以长是3cm的直角边为轴进行旋转,得到的圆锥的底面积最大 3.14×42=50.24(cm2)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
