2014学年度大庆市房顶中学第二学期初三数学第一次月考(含答案)
文档属性
| 名称 | 2014学年度大庆市房顶中学第二学期初三数学第一次月考(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 137.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-03-30 14:21:40 | ||
图片预览


文档简介
2014学年度大庆市房顶中学第二学期初三数学第一次月考
一.选择题(共14小题)
1.如果两个三角形的两条边和其中一条边上的高对应相等,那么这两个三角形的第三条边所对的角的关系是( )
A. 相等 B. 互余 C. 互补或相等 D. 不相等
2.△ABC中AB=AC,∠A=36°,BD平分∠ABC交AC于D,则图中的等腰三角形有( )
A. 1个 B. 2个 C. 3个 D. 4个
3.如图,CD是Rt△ABC斜边AB上的高,将△BCD沿CD折叠,B点恰好落在AB的中点E处,则∠A等于( )
A. 25° B. 30° C. 45° D. 60°
4.用含30°角的两块同样大小的直角三角板拼图形,下列四种图形:①平行四边形,②菱形,③矩形,④直角梯形,其中可以被拼成的图形是( )
A. ①② B. ①③ C. ③④ D. ①②③
5.能使两个直角三角形全等的条件是( )
A. 斜边相等 B. 一锐角对应相等 C. 两锐角对应相等 D. 两直角边对应相等
6.如图所示,在Rt△ABC中,∠A=90°,BD平分∠ABC,交AC于点D,且AB=4,BD=5,则点D到BC的距离是( )
A. 3 B. 4 C. 5 D. 6
2题 3题 6题 7题 9题
10题 15题 16题 17题 18题
19题 20题 21题 22题
7.如图,在Rt△ABC中,∠ACB=90°,BC=3,AC=4,AB的垂直平分线DE交BC的延长线于点E,则CE的长为( )
A. B. C. D. 2
8.到三角形三条边的距离都相等的点是这个三角形的( )
A. 三条中线的交点 B. 三条高的交点
C. 三条边的垂直平分线的交点 D. 三条角平分线的交点
9.已知△ABC的面积为36,将△ABC沿BC的方向平移到△A′B′C的位置,使B′和C重合,连接AC′交A′C于D,则△C′DC的面积为( )
A. 6 B. 9 C. 12 D. 18
10.已知:菱形ABCD中,对角线AC与BD相交于点O,OE∥DC交BC于点E,AD=6cm,则OE的长为( )
A. 6cm B. 4cm C. 3cm D. 2cm
11.活动课上,老师让同学们做一个对角线互相垂直的等腰梯形形状的风筝,其面积为450cm2,则两条对角线所用的竹条至少需要( )
A. 30cm B. 60cm C. 45cm D. 90cm
12.下列说法中,错误的是( )
A. 平行四边形的对角线互相平分 B. 对角线互相平分的四边形是平行四边形
C. 菱形的对角线互相垂直 D. 对角线互相垂直的四边形是菱形
13.△ABC中,AB=AC=5,BC=6,点D是BC上的一点,那么点D到AB与AC的距离的和为( )
A. 5 B. 6 C. 4 D.
14.在正方形ABCD的边AB、BC、CD、DA上分别任意取点E、F、G、H.这样得到的四边形EFGH中,是正方形的有( )
A. 1个 B. 2个 C. 4个 D. 无穷多个
二.填空题(共8小题)
15.如图,点B、F、C、E在同一条直线上,点A、D在直线BE的两侧,AB∥DE,BF=CE,请添加一个适当的条件: _________ ,使得AC=DF.
16.如图,在△ABC中,AB=AC,D、E是△ABC内两点,AD平分∠BAC,∠EBC=∠E=60°,若BE=6cm,DE=2cm,则BC= _________ .
17.如图,∠C=∠E=90°,AC=3,BC=4,AE=2,则AD= _________ .
18.在Rt△ABC中,∠C=90°,若BC=10,AD平分∠BAC交BC于点D,且BD:CD=3:2,则点D到线段AB的距离为 _________ .
19.如图, ABCD中,∠ABC=60°,E、F分别在CD和BC的延长线上,AE∥BD,EF⊥BC,EF=,则AB的长是 _________ .
20.如图,五边形ABCDE中,AB⊥BC,AE∥CD,∠A=∠E=120°,AB=CD=1,AE=2,则五边形ABCDE的面积等于 _________ .
21.如图,一个平行四边形的活动框架,对角线是两根橡皮筋.若改变框架的形状,则∠α也随之变化,两条对角线长度也在发生改变.当∠α为 _________ 度时,两条对角线长度相等.
22.如图,两张宽度均为3cm的纸条交错叠放在一起,相交成锐角α,且两张纸片中重叠部分的面积为9cm2,则锐角α的度数 _________ .
三.解答题(共6小题)
23.如图,在△ABC中,AB=AC,AD平分∠BAC.求证:∠DBC=∠DCB.
24.已知AD⊥BC,BE=CE,∠ABC=2∠C,BF为∠B的平分线.求证:AB=2DE.
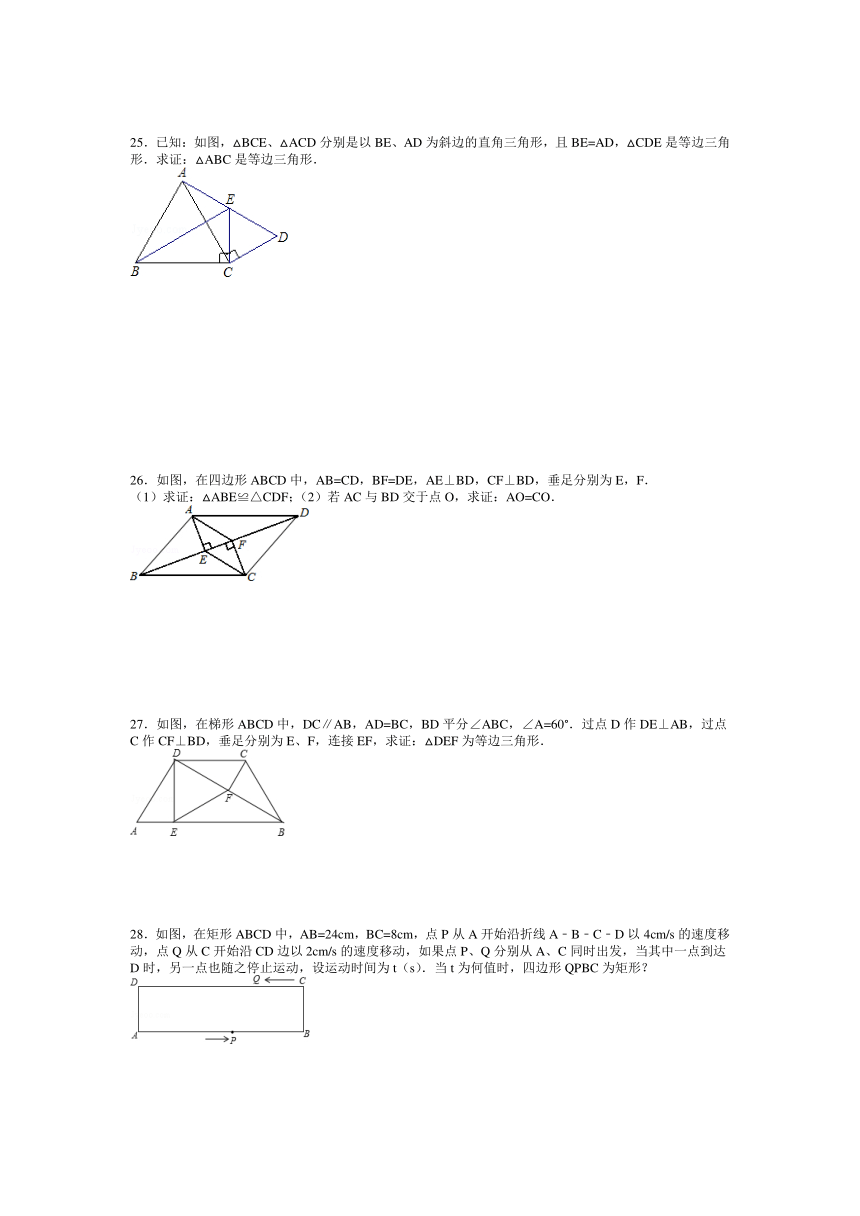
25.已知:如图,△BCE、△ACD分别是以BE、AD为斜边的直角三角形,且BE=AD,△CDE是等边三角形.求证:△ABC是等边三角形.
26.如图,在四边形ABCD中,AB=CD,BF=DE,AE⊥BD,CF⊥BD,垂足分别为E,F.
(1)求证:△ABE≌△CDF;(2)若AC与BD交于点O,求证:AO=CO.
27.如图,在梯形ABCD中,DC∥AB,AD=BC,BD平分∠ABC,∠A=60°.过点D作DE⊥AB,过点C作CF⊥BD,垂足分别为E、F,连接EF,求证:△DEF为等边三角形.
28.如图,在矩形ABCD中,AB=24cm,BC=8cm,点P从A开始沿折线A﹣B﹣C﹣D以4cm/s的速度移动,点Q从C开始沿CD边以2cm/s的速度移动,如果点P、Q分别从A、C同时出发,当其中一点到达D时,另一点也随之停止运动,设运动时间为t(s).当t为何值时,四边形QPBC为矩形?
2014学年度大庆市房顶中学第二学期初三数学第一次月考答案
一.选择题(共14小题)
1.C
2.C
3.B
4.B
5.D
6.A
7.B
8.D
9.D
10.C
11.D
13.D
14.D
二.填空题(共8小题)
15. AB=DE
16. 8cm .
17. .
18. 4 .
19. 1 .
20. .
21. 90
22. 45° .
三.解答题(共6小题)
23.(2012 常州)如图,在△ABC中,AB=AC,AD平分∠BAC.求证:∠DBC=∠DCB.
解答: 解:∵AD平分∠BAC,
∴∠BAD=∠CAD.
∴在△ACD和△ABD中
,
∴△ACD≌△ABD,
∴BD=CD,
∴∠DBC=∠DCB.
24.已知AD⊥BC,BE=CE,∠ABC=2∠C,BF为∠B的平分线.
求证:AB=2DE.
解答: 证明:连接EF.
∵∠ABC=2∠C,BF为∠B的平分线,
∴∠FBC=∠C=∠ABC,
∴BF=CF(等角对等边);
又∵BE=CE(已知),
∴EF⊥BC;
∵AD⊥BC,
∴EF∥AD,
∴AF:FC=DE:EC(平行线分线段成比例);
而AB:BC=AF:FC(角平分线的性质),
∴AB:BC=DE:EC(等量代换),
∴AB=2EC =2DE,即AB=2DE.
25.已知:如图,△BCE、△ACD分别是以BE、AD为斜边的直角三角形,且BE=AD,△CDE是等边三角形.求证:△ABC是等边三角形.
解答: 证明:∵△CDE是等边三角形,
∴EC=CD,∠1=60°.(1分)
∵BE、AD都是斜边,
∴∠BCE=∠ACD=90°(1分)
在Rt△BCE和Rt△ACD中,(1分)
∴Rt△BCE≌Rt△ACD(HL).(1分)
∴BC=AC.(1分)
∵∠1+∠2=90°,∠3+∠2=90°,
∴∠3=∠1=60°.(1分)
∴△ABC是等边三角形.
26.如图,在四边形ABCD中,AB=CD,BF=DE,AE⊥BD,CF⊥BD,垂足分别为E,F.
(1)求证:△ABE≌△CDF;
(2)若AC与BD交于点O,求证:AO=CO.
解答: 证明:(1)∵BF=DE,
∴BF﹣EF=DE﹣EF,
即BE=DF,
∵AE⊥BD,CF⊥BD,
∴∠AEB=∠CFD=90°,
∵AB=CD,
∴Rt△ABE≌Rt△CDF(HL);
(2)连接AC,
∵△ABE≌△CDF,
∴∠ABE=∠CDF,
∴AB∥CD,
∵AB=CD,
∴四边形ABCD是平行四边形,
∴AO=CO.
27.如图,在梯形ABCD中,DC∥AB,AD=BC,BD平分∠ABC,∠A=60°.过点D作DE⊥AB,过点C作CF⊥BD,垂足分别为E、F,连接EF,求证:△DEF为等边三角形.
解答: 证明:∵DC∥AB,AD=BC,∠A=60°,
∴∠A=∠ABC=60°,
∵BD平分∠ABC,
∴∠ABD=∠CBD=∠ABC=30°,
∵DC∥AB,
∴∠BDC=∠ABD=30°,
∴∠CDB=∠DBE
∴∠CBD=∠CDB,
∴CB=CD,
∵CF⊥BD,
∴F为BD的中点,
∵DE⊥AB,
∴DF=BF=EF,
由∠ABD=30°,得∠BDE=60°,
∴△DEF为等边三角形.
28.如图,在矩形ABCD中,AB=24cm,BC=8cm,点P从A开始沿折线A﹣B﹣C﹣D以4cm/s的速度移动,点Q从C开始沿CD边以2cm/s的速度移动,如果点P、Q分别从A、C同时出发,当其中一点到达D时,另一点也随之停止运动,设运动时间为t(s).当t为何值时,四边形QPBC为矩形?
解答: 解:根据题意得:CQ=2t,AP=4t,
则BP=24﹣4t,
∵四边形ABCD是矩形,
∴∠B=∠C=90°,CD∥AB,
∴只有CQ=BP时,四边形QPBC是矩形,
即2t=24﹣4t,
解得:t=4,
答:当t=4s时,四边形QPBC是矩形.
一.选择题(共14小题)
1.如果两个三角形的两条边和其中一条边上的高对应相等,那么这两个三角形的第三条边所对的角的关系是( )
A. 相等 B. 互余 C. 互补或相等 D. 不相等
2.△ABC中AB=AC,∠A=36°,BD平分∠ABC交AC于D,则图中的等腰三角形有( )
A. 1个 B. 2个 C. 3个 D. 4个
3.如图,CD是Rt△ABC斜边AB上的高,将△BCD沿CD折叠,B点恰好落在AB的中点E处,则∠A等于( )
A. 25° B. 30° C. 45° D. 60°
4.用含30°角的两块同样大小的直角三角板拼图形,下列四种图形:①平行四边形,②菱形,③矩形,④直角梯形,其中可以被拼成的图形是( )
A. ①② B. ①③ C. ③④ D. ①②③
5.能使两个直角三角形全等的条件是( )
A. 斜边相等 B. 一锐角对应相等 C. 两锐角对应相等 D. 两直角边对应相等
6.如图所示,在Rt△ABC中,∠A=90°,BD平分∠ABC,交AC于点D,且AB=4,BD=5,则点D到BC的距离是( )
A. 3 B. 4 C. 5 D. 6
2题 3题 6题 7题 9题
10题 15题 16题 17题 18题
19题 20题 21题 22题
7.如图,在Rt△ABC中,∠ACB=90°,BC=3,AC=4,AB的垂直平分线DE交BC的延长线于点E,则CE的长为( )
A. B. C. D. 2
8.到三角形三条边的距离都相等的点是这个三角形的( )
A. 三条中线的交点 B. 三条高的交点
C. 三条边的垂直平分线的交点 D. 三条角平分线的交点
9.已知△ABC的面积为36,将△ABC沿BC的方向平移到△A′B′C的位置,使B′和C重合,连接AC′交A′C于D,则△C′DC的面积为( )
A. 6 B. 9 C. 12 D. 18
10.已知:菱形ABCD中,对角线AC与BD相交于点O,OE∥DC交BC于点E,AD=6cm,则OE的长为( )
A. 6cm B. 4cm C. 3cm D. 2cm
11.活动课上,老师让同学们做一个对角线互相垂直的等腰梯形形状的风筝,其面积为450cm2,则两条对角线所用的竹条至少需要( )
A. 30cm B. 60cm C. 45cm D. 90cm
12.下列说法中,错误的是( )
A. 平行四边形的对角线互相平分 B. 对角线互相平分的四边形是平行四边形
C. 菱形的对角线互相垂直 D. 对角线互相垂直的四边形是菱形
13.△ABC中,AB=AC=5,BC=6,点D是BC上的一点,那么点D到AB与AC的距离的和为( )
A. 5 B. 6 C. 4 D.
14.在正方形ABCD的边AB、BC、CD、DA上分别任意取点E、F、G、H.这样得到的四边形EFGH中,是正方形的有( )
A. 1个 B. 2个 C. 4个 D. 无穷多个
二.填空题(共8小题)
15.如图,点B、F、C、E在同一条直线上,点A、D在直线BE的两侧,AB∥DE,BF=CE,请添加一个适当的条件: _________ ,使得AC=DF.
16.如图,在△ABC中,AB=AC,D、E是△ABC内两点,AD平分∠BAC,∠EBC=∠E=60°,若BE=6cm,DE=2cm,则BC= _________ .
17.如图,∠C=∠E=90°,AC=3,BC=4,AE=2,则AD= _________ .
18.在Rt△ABC中,∠C=90°,若BC=10,AD平分∠BAC交BC于点D,且BD:CD=3:2,则点D到线段AB的距离为 _________ .
19.如图, ABCD中,∠ABC=60°,E、F分别在CD和BC的延长线上,AE∥BD,EF⊥BC,EF=,则AB的长是 _________ .
20.如图,五边形ABCDE中,AB⊥BC,AE∥CD,∠A=∠E=120°,AB=CD=1,AE=2,则五边形ABCDE的面积等于 _________ .
21.如图,一个平行四边形的活动框架,对角线是两根橡皮筋.若改变框架的形状,则∠α也随之变化,两条对角线长度也在发生改变.当∠α为 _________ 度时,两条对角线长度相等.
22.如图,两张宽度均为3cm的纸条交错叠放在一起,相交成锐角α,且两张纸片中重叠部分的面积为9cm2,则锐角α的度数 _________ .
三.解答题(共6小题)
23.如图,在△ABC中,AB=AC,AD平分∠BAC.求证:∠DBC=∠DCB.
24.已知AD⊥BC,BE=CE,∠ABC=2∠C,BF为∠B的平分线.求证:AB=2DE.
25.已知:如图,△BCE、△ACD分别是以BE、AD为斜边的直角三角形,且BE=AD,△CDE是等边三角形.求证:△ABC是等边三角形.
26.如图,在四边形ABCD中,AB=CD,BF=DE,AE⊥BD,CF⊥BD,垂足分别为E,F.
(1)求证:△ABE≌△CDF;(2)若AC与BD交于点O,求证:AO=CO.
27.如图,在梯形ABCD中,DC∥AB,AD=BC,BD平分∠ABC,∠A=60°.过点D作DE⊥AB,过点C作CF⊥BD,垂足分别为E、F,连接EF,求证:△DEF为等边三角形.
28.如图,在矩形ABCD中,AB=24cm,BC=8cm,点P从A开始沿折线A﹣B﹣C﹣D以4cm/s的速度移动,点Q从C开始沿CD边以2cm/s的速度移动,如果点P、Q分别从A、C同时出发,当其中一点到达D时,另一点也随之停止运动,设运动时间为t(s).当t为何值时,四边形QPBC为矩形?
2014学年度大庆市房顶中学第二学期初三数学第一次月考答案
一.选择题(共14小题)
1.C
2.C
3.B
4.B
5.D
6.A
7.B
8.D
9.D
10.C
11.D
13.D
14.D
二.填空题(共8小题)
15. AB=DE
16. 8cm .
17. .
18. 4 .
19. 1 .
20. .
21. 90
22. 45° .
三.解答题(共6小题)
23.(2012 常州)如图,在△ABC中,AB=AC,AD平分∠BAC.求证:∠DBC=∠DCB.
解答: 解:∵AD平分∠BAC,
∴∠BAD=∠CAD.
∴在△ACD和△ABD中
,
∴△ACD≌△ABD,
∴BD=CD,
∴∠DBC=∠DCB.
24.已知AD⊥BC,BE=CE,∠ABC=2∠C,BF为∠B的平分线.
求证:AB=2DE.
解答: 证明:连接EF.
∵∠ABC=2∠C,BF为∠B的平分线,
∴∠FBC=∠C=∠ABC,
∴BF=CF(等角对等边);
又∵BE=CE(已知),
∴EF⊥BC;
∵AD⊥BC,
∴EF∥AD,
∴AF:FC=DE:EC(平行线分线段成比例);
而AB:BC=AF:FC(角平分线的性质),
∴AB:BC=DE:EC(等量代换),
∴AB=2EC =2DE,即AB=2DE.
25.已知:如图,△BCE、△ACD分别是以BE、AD为斜边的直角三角形,且BE=AD,△CDE是等边三角形.求证:△ABC是等边三角形.
解答: 证明:∵△CDE是等边三角形,
∴EC=CD,∠1=60°.(1分)
∵BE、AD都是斜边,
∴∠BCE=∠ACD=90°(1分)
在Rt△BCE和Rt△ACD中,(1分)
∴Rt△BCE≌Rt△ACD(HL).(1分)
∴BC=AC.(1分)
∵∠1+∠2=90°,∠3+∠2=90°,
∴∠3=∠1=60°.(1分)
∴△ABC是等边三角形.
26.如图,在四边形ABCD中,AB=CD,BF=DE,AE⊥BD,CF⊥BD,垂足分别为E,F.
(1)求证:△ABE≌△CDF;
(2)若AC与BD交于点O,求证:AO=CO.
解答: 证明:(1)∵BF=DE,
∴BF﹣EF=DE﹣EF,
即BE=DF,
∵AE⊥BD,CF⊥BD,
∴∠AEB=∠CFD=90°,
∵AB=CD,
∴Rt△ABE≌Rt△CDF(HL);
(2)连接AC,
∵△ABE≌△CDF,
∴∠ABE=∠CDF,
∴AB∥CD,
∵AB=CD,
∴四边形ABCD是平行四边形,
∴AO=CO.
27.如图,在梯形ABCD中,DC∥AB,AD=BC,BD平分∠ABC,∠A=60°.过点D作DE⊥AB,过点C作CF⊥BD,垂足分别为E、F,连接EF,求证:△DEF为等边三角形.
解答: 证明:∵DC∥AB,AD=BC,∠A=60°,
∴∠A=∠ABC=60°,
∵BD平分∠ABC,
∴∠ABD=∠CBD=∠ABC=30°,
∵DC∥AB,
∴∠BDC=∠ABD=30°,
∴∠CDB=∠DBE
∴∠CBD=∠CDB,
∴CB=CD,
∵CF⊥BD,
∴F为BD的中点,
∵DE⊥AB,
∴DF=BF=EF,
由∠ABD=30°,得∠BDE=60°,
∴△DEF为等边三角形.
28.如图,在矩形ABCD中,AB=24cm,BC=8cm,点P从A开始沿折线A﹣B﹣C﹣D以4cm/s的速度移动,点Q从C开始沿CD边以2cm/s的速度移动,如果点P、Q分别从A、C同时出发,当其中一点到达D时,另一点也随之停止运动,设运动时间为t(s).当t为何值时,四边形QPBC为矩形?
解答: 解:根据题意得:CQ=2t,AP=4t,
则BP=24﹣4t,
∵四边形ABCD是矩形,
∴∠B=∠C=90°,CD∥AB,
∴只有CQ=BP时,四边形QPBC是矩形,
即2t=24﹣4t,
解得:t=4,
答:当t=4s时,四边形QPBC是矩形.
同课章节目录
