26.3实践与探索(二次函数的实际问题) 课时练习(含解析)2022-2023学年华东师大版数学九年级下册
文档属性
| 名称 | 26.3实践与探索(二次函数的实际问题) 课时练习(含解析)2022-2023学年华东师大版数学九年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-23 00:00:00 | ||
图片预览



文档简介
26.3实践与探索(二次函数的实际问题)测试
学校:___________姓名:___________班级:___________考号:___________
满分120分 考试时间120分钟
一、单选题(每小题4分,共48分)
1.向空中发射一枚炮弹,经过秒后高度为米,且时间与高度的关系式为,若炮弹在第6秒与第14秒时的高度相等,则炮弹所在高度最高的时间是( )
A.第8秒 B.第9秒 C.第10秒 D.第11秒
2.一个人以6米/秒的匀速度去追赶停在交通灯前的汽车,当他离汽车米时交通灯由红变绿,汽车开始做变速直线行驶(汽车与人的前进方向相同),汽车在时刻t的路程,那么,此人( )
A.可在7秒内追上汽车 B.可在9秒内追上汽车
C.不能追上汽车,但期间最近距离为米 D.不能追上汽车,但期间最近距离为7米
3.某厂家2022年2月份生产口罩产量为180万只,4月份生产口罩的产量为461万只,设从2月份到4月份该厂家口罩产量的平均月增长率为x,根据题意可得方程( )
A. B. C. D.
4.如图,一位篮球运动员投篮,球沿抛物线运行,然后准确落入篮筐内,已知篮筐的中心离地面的高度为,则他距篮筐中心的水平距离是( )m.
A.1 B.2 C.3 D.4
5.2022年北京冬奥会的冰墩墩受广大群众的喜爱,某超市销售冰墩墩饰品,每件成本为40元,销售人员经调查发现,该商品每月的销售量y(件)与销售单价x(元)之间满足函数关系式,若要求销售单价不得低于成本.为了每月所获利润最大,该商品销售单价应定为多少元?每月最大利润是多少元?( )
A.80元,1800元 B.70元,2000元 C.70元,1800元 D.80元,2000元
6.如图,一座拱桥的轮廓是抛物线型,拱高,跨度,相邻两支柱间的距离均为,请根据所给的数据,则支柱的长度为( )
A.4.5 B.5 C.5.5 D.6
7.18岁的中国选手谷爱凌在北京2022年冬奥会比赛中夺得3枚金牌,被誉为“雪上公主”,谷爱凌从山坡上滑下,其滑行距离(单位:m)与滑行时间(单位:s)之间的关系可以近似地用二次函数刻画,其图像如图所示,根据图像,当滑行时间为时,滑行距离为( )
A.30 B.28.5 C.26.5 D.29
8.如图,晓波家的院墙一边靠墙处,用米长的铁栅栏围成了三个相连的养殖小院子,总面积为平方米,为方便喂养这些不同类的动物,在各个养殖院子之间留出了米宽的缺口作通道,在平行于墙的一边留下一个米宽的缺口作小门.若设米,则关于的函数关系式为( )
A. B. C. D.
9.为了美观,在加工太阳镜时将下半部分轮廓制作成抛物线的形状(如图)对应的两条抛物线关于y轴对称,轴,,最低点C在x轴上,高,.则左轮廓线所在抛物线的函数解析式为( )
A. B. C. D.
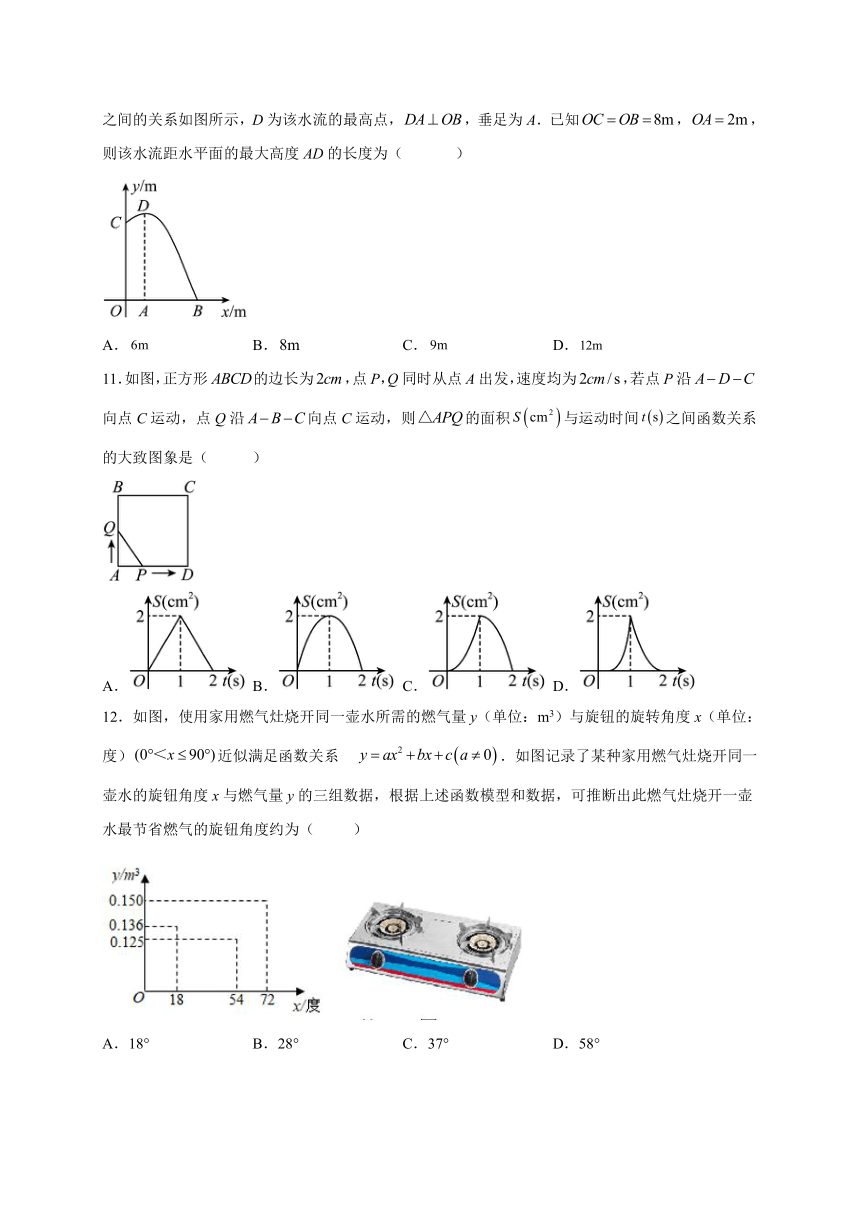
10.某景点的“喷水巨龙”口中C处的水流量抛物线形,该水流喷出的高度y(m)与水平距离x(m)之间的关系如图所示,D为该水流的最高点,,垂足为A.已知,,则该水流距水平面的最大高度AD的长度为( )
A. B. C. D.
11.如图,正方形的边长为,点P,Q同时从点A出发,速度均为,若点P沿向点C运动,点Q沿向点C运动,则的面积与运动时间之间函数关系的大致图象是( )
A. B. C. D.
12.如图,使用家用燃气灶烧开同一壶水所需的燃气量y(单位:m3)与旋钮的旋转角度x(单位:度)近似满足函数关系 .如图记录了某种家用燃气灶烧开同一壶水的旋钮角度x与燃气量y的三组数据,根据上述函数模型和数据,可推断出此燃气灶烧开一壶水最节省燃气的旋钮角度约为( )
A.18° B.28° C.37° D.58°
二、填空题(每小题4分,共16分)
13.用一段长的篱笆围成一个一边靠墙的矩形菜园,墙长为,设这个矩形的宽为,则矩形面积随变化的函数解析式为____________.
14.如图,抛物线的顶点为点P,点Q是该抛物线上一点,若将抛物线向左平移得到一条新抛物线,其中点P,,平移后的对应点分别为点,若曲线段扫过的面积为15(图中阴影部分),则新抛物线的解析式为__________.
15.“水幕电影”的工作原理是把影像打在抛物线状的水幕上,通过光学原理折射出图像,水幕是由若干个水嘴喷出的水柱组成的(如图),水柱的最高点为P,m,m,水嘴高m,则水柱落地点C到水嘴所在墙的距离是___________m.
16.廊桥是我国古老的文化遗产.如图,是某座抛物线型的廊桥示意图,已知抛物线的函数表达式为,为保护廊桥的安全,在该抛物线上距水面高为8米的点E,F处要安装两盏警示灯,则这两盏灯的水平距离是_________米.
三、解答题(6个小题,共56分)
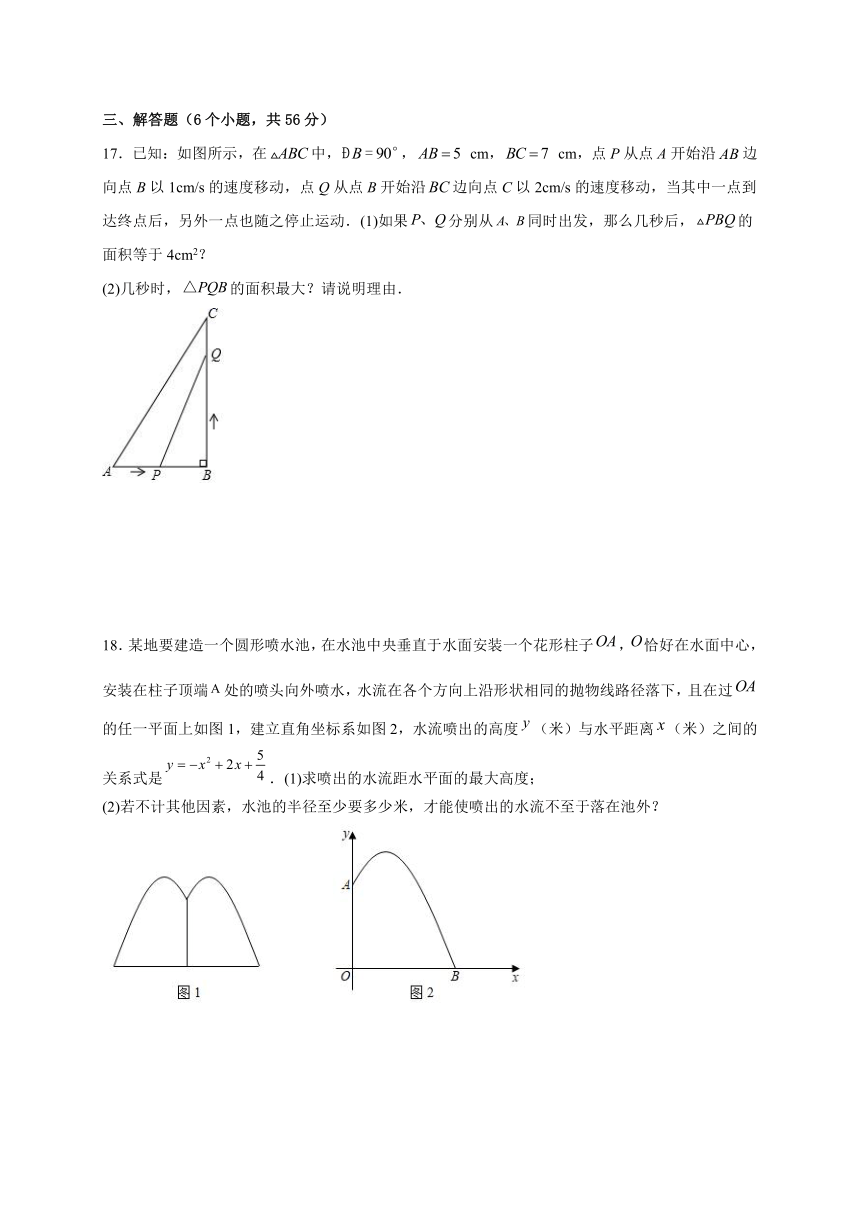
17.已知:如图所示,在中,, cm, cm,点P从点A开始沿边向点B以1cm/s的速度移动,点Q从点B开始沿边向点C以2cm/s的速度移动,当其中一点到达终点后,另外一点也随之停止运动.(1)如果分别从同时出发,那么几秒后,的面积等于4cm2?
(2)几秒时,的面积最大?请说明理由.
18.某地要建造一个圆形喷水池,在水池中央垂直于水面安装一个花形柱子,恰好在水面中心,安装在柱子顶端处的喷头向外喷水,水流在各个方向上沿形状相同的抛物线路径落下,且在过的任一平面上如图1,建立直角坐标系如图2,水流喷出的高度(米)与水平距离(米)之间的关系式是.(1)求喷出的水流距水平面的最大高度;
(2)若不计其他因素,水池的半径至少要多少米,才能使喷出的水流不至于落在池外?
19.为了有效预防和控制疫情,及时监测疫情发展态势,实施定期核酸检测.某社区准备搭建一个动态核酸检测点,现有33米可移动的隔离带,围成如图的临时检测点,这是一个一面靠墙(墙面为)的矩形,内部分成两个区,区为登记区,区为检测区,入口通道在边上,两区通道在边上,出口通道在边上,通道宽均为1米.设,矩形的面积为.
(1)可表示为________;
(2)当为何值时,有最大值?最大值是多少?
(3)所围成矩形的面积能否达到96平方米?如果能,求出的长;如果不能,请说明理由.
20.如图,隧道的截面由抛物线和长方形构成.长方形的长是,宽是.按照图中所示的平面直角坐标系,抛物线可以用表示.
(1)求抛物线的函数表达式,并计算出拱顶到地面的距离.
(2)一辆货运汽车载一长方体集装箱后高为,宽为,如果隧道内设双向车道,那么这辆货车能否安全通过?
(3)在抛物线形拱壁上需要安装两排灯,使它们离地面的高度相等,如果灯离地面的高度不超过,那么两排灯的水平距离最小是___________.
21.某运动器材批发市场销售一种篮球,每个篮球进价为元,规定每个篮球的售价不低于进价.经市场调查,每月的销售量(个)与每个篮球的售价(元)满足一次函数关系,部分数据如下表:
售价
销售量
(1)求与之间的函数关系式;(不需求自变量x的取值范围)
(2)该批发市场每月想从这种篮球销售中获利元,又想尽量多给客户实惠,应如何给这种篮球定价?
(3)物价部门规定,该篮球的每个利润不允许高于进货价的,设销售这种篮球每月的总利润为w(元),那么销售单价定为多少元可获得最大利润?最大利润是多少?
22.如图1,小兵和小伙伴一起玩扔小石头游戏,我们把小石头的运动轨迹看成是抛物线的一部分.
如图2所示,以点O为原点建立平面直角坐标系.已知扔小石头的出手点A在点O正上方2米的位置,小石头在与点O的水平距离为6米时达到最高高度5米;为扔小石头的预期击中目标,点B在x轴上,离点O的水平距离为12米,点C在点B的正上方2米.
(1)小兵扔的小石头能否正好击中点C,并说明理由;
(2)求小石头运动轨迹所在抛物线的解析式;
(3)直接写出小石头在运动过程中与直线的最大竖直距离.
参考答案:
1.C
【详解】解:∵此炮弹在第6与第14秒时的高度相等,
∴抛物线的对称轴是直线,
∴炮弹所在高度最高是10秒,
故选:C.
2.D
【详解】解:根据题意得,车与人的间距:,
即当s时,d取最小值7,
故不能追上汽车,当s时,期间最近距离为7米,
故选:D.
3.B
【详解】解:根据题意得,
故选:B.
4.D
【详解】当时,
,
解得:,
结合图象可知,.
故选:D.
5.C
【详解】设每月所获利润为,
由题意可知:
,
∵抛物线开口向下,
∴当时,函数有最大值为1800.
故选:C.
6.C
【详解】解:如图所示,建立平面直角坐标系,
由题意得A点坐标,B点坐标为,C点坐标为,N点横坐标为5,
设抛物线解析式为,
∴,
∴,
∴抛物线解析式为,
∴当时,,
∴支柱的高度m,
故选:C.
7.B
【详解】解:设抛物线的解析式为: ,
由图像可知,图像经过点、,
∴,
∴,
∴,
∴当滑行时间为时,,
故选:B.
8.D
【详解】解:如图所示,
设米,则,
又小院子的总面积为,
∴,
故选:.
9.B
【详解】解:∵高,,B、D关于y轴对称,
∴B点坐标为,
∵轴,,最低点C在x轴上,
∴关于直线对称,
∴左边抛物线的顶点C的坐标为,
设左边抛物线的解析式为,
把代入得,解得,
故左边抛物线的解析式为,
故选:B.
10.C
【详解】解:根据题意,设抛物线解析式为,
将点、代入,得:,解得,
∴抛物线解析式为,
所以当时,,即
故选:C.
11.C
【详解】解:当Q、P两点分别在、上时,,,
的面积为:,;
当Q、P两点分别在、上时,连接,如图所示:
根据题意有:,则,
∵正方形的边长为,
∴,
∴,
同理可得,
∵根据的面积为正方形的面积减去面积、面积和面积,
∴,
∴,
∴,,
则有,故C正确.
故选:C.
12.C
【详解】解:根据题意可知抛物线的开口向上,由已知的三个点描点、连线得到函数的大致图像,
由图知抛物线的对称轴的位置在36和54之间,比36 稍大,大约37.
因此可推断出此燃气灶烧开一壶水最节省燃气的旋钮角度约为37°.
故选:C.
13.
【详解】解:这个矩形的宽为,
这个矩形的长为,
由题意可得,
,
故答案为:.
14.
【详解】解:∵抛物线的顶点为点P,
∴,
曲线段扫过的面积,则,
故抛物线向左平移5个单位,则,
故答案为:.
15.5
【详解】解:以A为坐标原点,所在的直线为x轴,所在的直线为y轴建立平面直角坐标系,如图所示,
则,,,
∵点P是最高点,
∴设抛物线的解析式为:,
将点D坐标代入,可得:,解得:,
∴,
令,解得:,,
∴点,
∴,
故答案为:5.
16.18
【详解】解:由“在该抛物线上距水面高为8米的点”,
可知,
把代入得:
,解得,
由两点间距离公式可求出(米.
故答案为:18.
17.(1)见解析;(2)见解析
【详解】(1)解:设经过x秒以后面积为,则
,
整理得:,解得:,
∵当时,,
∴不合题意,
答:1秒后的面积等于;
(2)解:当秒时,面积最大.理由如下:
设经过t秒以后面积最大,则
,
当秒时,面积最大.
18.(1)2.25米;(2)2.5米
【详解】(1)解:,
顶点是,
故喷出的水流距水面的最大高度是2.25米;
(2)解:解方程,得,,
点坐标为,
.
故不计其他因素,水池的半径至少要2.5米,才能使喷出的水流不至于落在水池外.
19.(1)
(2)当时,有最大值,最大值是108
(3)能围成96平方米的面积,此时的长为4米或8米
【详解】(1)解:根据题意得:,
∴,
∴米,
则可表示为:,
故答案为:;
(2)解:根据题意得:,
∵,
∴当时,有最大值,最大值是108;
(3)能
∵,
∴,
∴,
∴或,
答:能围成96平方米的面积,此时的长为4米或8米.
20.(1),拱顶到地面的距离为米;(2)这辆货车不能安全通过,理由见解析;
(3)
【详解】(1)解:∵长方形的长是,宽是,
∴,,
代入,得:,解得:,
∴抛物线解析为,
∴顶点的坐标为;
∴拱顶到地面的距离为米;
(2)解:由(1)可知,抛物线的对称轴为直线,
∴货运汽车最外侧与地面的交点为或,
令或,得,
∴这辆货车不能安全通过;
(3)解:依题意,当时,,解得:
∴
∴两排灯的水平距离最小是米,
故答案为:.
21.(1);(2)元;(3)售价定为元可获得最大利润,最大利润是元
【详解】(1)解:设与之间的函数关系式为,
,解得,即与之间的函数表达式是;
(2)解:,解得,
∵尽量给客户优惠,
∴这种衬衫定价为元;
(3)解:由题意可得,
,
∵该衬衫的每件利润不允许高于进货价的,每件售价不低于进货价,
∴,,解得,
∴当时,取得最大值,此时,
答:售价定为元可获得最大利润,最大利润是元.
22.(1)小兵扔的小石头能击中点C,理由见解析
(2)
(3)小石头在运动过程中与直线的最大竖直距离为
【详解】(1)解:小兵扔的小石头能击中点C,理由如下:
∵根据题意,可得:抛物线的对称轴为,
又∵根据题意,可得:,,
∴点和点关于对称,
∴点在抛物线上,
∴小兵扔的小石头能击中点C;
(2)解:根据题意,可得:抛物线的顶点坐标为,
∴设抛物线的解析式为,
又∵点经过抛物线,
∴把的坐标代入解析式,可得:,解得:,
∴抛物线的解析式为,
又∵根据题意,可得:该抛物线的自变量的取值范围为,
∴小石头运动轨迹所在抛物线的解析式为,
(3)解:如图,连接,设直线的解析式为,
把代入,可得:,解得:,
∴直线的解析式为,
设直线上方的抛物线上的一点的坐标为,
过点作轴,交于点,则的坐标为,
∴,
∴当时,有最大值,最大值为,
∴小石头在运动过程中与直线的最大竖直距离为.
学校:___________姓名:___________班级:___________考号:___________
满分120分 考试时间120分钟
一、单选题(每小题4分,共48分)
1.向空中发射一枚炮弹,经过秒后高度为米,且时间与高度的关系式为,若炮弹在第6秒与第14秒时的高度相等,则炮弹所在高度最高的时间是( )
A.第8秒 B.第9秒 C.第10秒 D.第11秒
2.一个人以6米/秒的匀速度去追赶停在交通灯前的汽车,当他离汽车米时交通灯由红变绿,汽车开始做变速直线行驶(汽车与人的前进方向相同),汽车在时刻t的路程,那么,此人( )
A.可在7秒内追上汽车 B.可在9秒内追上汽车
C.不能追上汽车,但期间最近距离为米 D.不能追上汽车,但期间最近距离为7米
3.某厂家2022年2月份生产口罩产量为180万只,4月份生产口罩的产量为461万只,设从2月份到4月份该厂家口罩产量的平均月增长率为x,根据题意可得方程( )
A. B. C. D.
4.如图,一位篮球运动员投篮,球沿抛物线运行,然后准确落入篮筐内,已知篮筐的中心离地面的高度为,则他距篮筐中心的水平距离是( )m.
A.1 B.2 C.3 D.4
5.2022年北京冬奥会的冰墩墩受广大群众的喜爱,某超市销售冰墩墩饰品,每件成本为40元,销售人员经调查发现,该商品每月的销售量y(件)与销售单价x(元)之间满足函数关系式,若要求销售单价不得低于成本.为了每月所获利润最大,该商品销售单价应定为多少元?每月最大利润是多少元?( )
A.80元,1800元 B.70元,2000元 C.70元,1800元 D.80元,2000元
6.如图,一座拱桥的轮廓是抛物线型,拱高,跨度,相邻两支柱间的距离均为,请根据所给的数据,则支柱的长度为( )
A.4.5 B.5 C.5.5 D.6
7.18岁的中国选手谷爱凌在北京2022年冬奥会比赛中夺得3枚金牌,被誉为“雪上公主”,谷爱凌从山坡上滑下,其滑行距离(单位:m)与滑行时间(单位:s)之间的关系可以近似地用二次函数刻画,其图像如图所示,根据图像,当滑行时间为时,滑行距离为( )
A.30 B.28.5 C.26.5 D.29
8.如图,晓波家的院墙一边靠墙处,用米长的铁栅栏围成了三个相连的养殖小院子,总面积为平方米,为方便喂养这些不同类的动物,在各个养殖院子之间留出了米宽的缺口作通道,在平行于墙的一边留下一个米宽的缺口作小门.若设米,则关于的函数关系式为( )
A. B. C. D.
9.为了美观,在加工太阳镜时将下半部分轮廓制作成抛物线的形状(如图)对应的两条抛物线关于y轴对称,轴,,最低点C在x轴上,高,.则左轮廓线所在抛物线的函数解析式为( )
A. B. C. D.
10.某景点的“喷水巨龙”口中C处的水流量抛物线形,该水流喷出的高度y(m)与水平距离x(m)之间的关系如图所示,D为该水流的最高点,,垂足为A.已知,,则该水流距水平面的最大高度AD的长度为( )
A. B. C. D.
11.如图,正方形的边长为,点P,Q同时从点A出发,速度均为,若点P沿向点C运动,点Q沿向点C运动,则的面积与运动时间之间函数关系的大致图象是( )
A. B. C. D.
12.如图,使用家用燃气灶烧开同一壶水所需的燃气量y(单位:m3)与旋钮的旋转角度x(单位:度)近似满足函数关系 .如图记录了某种家用燃气灶烧开同一壶水的旋钮角度x与燃气量y的三组数据,根据上述函数模型和数据,可推断出此燃气灶烧开一壶水最节省燃气的旋钮角度约为( )
A.18° B.28° C.37° D.58°
二、填空题(每小题4分,共16分)
13.用一段长的篱笆围成一个一边靠墙的矩形菜园,墙长为,设这个矩形的宽为,则矩形面积随变化的函数解析式为____________.
14.如图,抛物线的顶点为点P,点Q是该抛物线上一点,若将抛物线向左平移得到一条新抛物线,其中点P,,平移后的对应点分别为点,若曲线段扫过的面积为15(图中阴影部分),则新抛物线的解析式为__________.
15.“水幕电影”的工作原理是把影像打在抛物线状的水幕上,通过光学原理折射出图像,水幕是由若干个水嘴喷出的水柱组成的(如图),水柱的最高点为P,m,m,水嘴高m,则水柱落地点C到水嘴所在墙的距离是___________m.
16.廊桥是我国古老的文化遗产.如图,是某座抛物线型的廊桥示意图,已知抛物线的函数表达式为,为保护廊桥的安全,在该抛物线上距水面高为8米的点E,F处要安装两盏警示灯,则这两盏灯的水平距离是_________米.
三、解答题(6个小题,共56分)
17.已知:如图所示,在中,, cm, cm,点P从点A开始沿边向点B以1cm/s的速度移动,点Q从点B开始沿边向点C以2cm/s的速度移动,当其中一点到达终点后,另外一点也随之停止运动.(1)如果分别从同时出发,那么几秒后,的面积等于4cm2?
(2)几秒时,的面积最大?请说明理由.
18.某地要建造一个圆形喷水池,在水池中央垂直于水面安装一个花形柱子,恰好在水面中心,安装在柱子顶端处的喷头向外喷水,水流在各个方向上沿形状相同的抛物线路径落下,且在过的任一平面上如图1,建立直角坐标系如图2,水流喷出的高度(米)与水平距离(米)之间的关系式是.(1)求喷出的水流距水平面的最大高度;
(2)若不计其他因素,水池的半径至少要多少米,才能使喷出的水流不至于落在池外?
19.为了有效预防和控制疫情,及时监测疫情发展态势,实施定期核酸检测.某社区准备搭建一个动态核酸检测点,现有33米可移动的隔离带,围成如图的临时检测点,这是一个一面靠墙(墙面为)的矩形,内部分成两个区,区为登记区,区为检测区,入口通道在边上,两区通道在边上,出口通道在边上,通道宽均为1米.设,矩形的面积为.
(1)可表示为________;
(2)当为何值时,有最大值?最大值是多少?
(3)所围成矩形的面积能否达到96平方米?如果能,求出的长;如果不能,请说明理由.
20.如图,隧道的截面由抛物线和长方形构成.长方形的长是,宽是.按照图中所示的平面直角坐标系,抛物线可以用表示.
(1)求抛物线的函数表达式,并计算出拱顶到地面的距离.
(2)一辆货运汽车载一长方体集装箱后高为,宽为,如果隧道内设双向车道,那么这辆货车能否安全通过?
(3)在抛物线形拱壁上需要安装两排灯,使它们离地面的高度相等,如果灯离地面的高度不超过,那么两排灯的水平距离最小是___________.
21.某运动器材批发市场销售一种篮球,每个篮球进价为元,规定每个篮球的售价不低于进价.经市场调查,每月的销售量(个)与每个篮球的售价(元)满足一次函数关系,部分数据如下表:
售价
销售量
(1)求与之间的函数关系式;(不需求自变量x的取值范围)
(2)该批发市场每月想从这种篮球销售中获利元,又想尽量多给客户实惠,应如何给这种篮球定价?
(3)物价部门规定,该篮球的每个利润不允许高于进货价的,设销售这种篮球每月的总利润为w(元),那么销售单价定为多少元可获得最大利润?最大利润是多少?
22.如图1,小兵和小伙伴一起玩扔小石头游戏,我们把小石头的运动轨迹看成是抛物线的一部分.
如图2所示,以点O为原点建立平面直角坐标系.已知扔小石头的出手点A在点O正上方2米的位置,小石头在与点O的水平距离为6米时达到最高高度5米;为扔小石头的预期击中目标,点B在x轴上,离点O的水平距离为12米,点C在点B的正上方2米.
(1)小兵扔的小石头能否正好击中点C,并说明理由;
(2)求小石头运动轨迹所在抛物线的解析式;
(3)直接写出小石头在运动过程中与直线的最大竖直距离.
参考答案:
1.C
【详解】解:∵此炮弹在第6与第14秒时的高度相等,
∴抛物线的对称轴是直线,
∴炮弹所在高度最高是10秒,
故选:C.
2.D
【详解】解:根据题意得,车与人的间距:,
即当s时,d取最小值7,
故不能追上汽车,当s时,期间最近距离为7米,
故选:D.
3.B
【详解】解:根据题意得,
故选:B.
4.D
【详解】当时,
,
解得:,
结合图象可知,.
故选:D.
5.C
【详解】设每月所获利润为,
由题意可知:
,
∵抛物线开口向下,
∴当时,函数有最大值为1800.
故选:C.
6.C
【详解】解:如图所示,建立平面直角坐标系,
由题意得A点坐标,B点坐标为,C点坐标为,N点横坐标为5,
设抛物线解析式为,
∴,
∴,
∴抛物线解析式为,
∴当时,,
∴支柱的高度m,
故选:C.
7.B
【详解】解:设抛物线的解析式为: ,
由图像可知,图像经过点、,
∴,
∴,
∴,
∴当滑行时间为时,,
故选:B.
8.D
【详解】解:如图所示,
设米,则,
又小院子的总面积为,
∴,
故选:.
9.B
【详解】解:∵高,,B、D关于y轴对称,
∴B点坐标为,
∵轴,,最低点C在x轴上,
∴关于直线对称,
∴左边抛物线的顶点C的坐标为,
设左边抛物线的解析式为,
把代入得,解得,
故左边抛物线的解析式为,
故选:B.
10.C
【详解】解:根据题意,设抛物线解析式为,
将点、代入,得:,解得,
∴抛物线解析式为,
所以当时,,即
故选:C.
11.C
【详解】解:当Q、P两点分别在、上时,,,
的面积为:,;
当Q、P两点分别在、上时,连接,如图所示:
根据题意有:,则,
∵正方形的边长为,
∴,
∴,
同理可得,
∵根据的面积为正方形的面积减去面积、面积和面积,
∴,
∴,
∴,,
则有,故C正确.
故选:C.
12.C
【详解】解:根据题意可知抛物线的开口向上,由已知的三个点描点、连线得到函数的大致图像,
由图知抛物线的对称轴的位置在36和54之间,比36 稍大,大约37.
因此可推断出此燃气灶烧开一壶水最节省燃气的旋钮角度约为37°.
故选:C.
13.
【详解】解:这个矩形的宽为,
这个矩形的长为,
由题意可得,
,
故答案为:.
14.
【详解】解:∵抛物线的顶点为点P,
∴,
曲线段扫过的面积,则,
故抛物线向左平移5个单位,则,
故答案为:.
15.5
【详解】解:以A为坐标原点,所在的直线为x轴,所在的直线为y轴建立平面直角坐标系,如图所示,
则,,,
∵点P是最高点,
∴设抛物线的解析式为:,
将点D坐标代入,可得:,解得:,
∴,
令,解得:,,
∴点,
∴,
故答案为:5.
16.18
【详解】解:由“在该抛物线上距水面高为8米的点”,
可知,
把代入得:
,解得,
由两点间距离公式可求出(米.
故答案为:18.
17.(1)见解析;(2)见解析
【详解】(1)解:设经过x秒以后面积为,则
,
整理得:,解得:,
∵当时,,
∴不合题意,
答:1秒后的面积等于;
(2)解:当秒时,面积最大.理由如下:
设经过t秒以后面积最大,则
,
当秒时,面积最大.
18.(1)2.25米;(2)2.5米
【详解】(1)解:,
顶点是,
故喷出的水流距水面的最大高度是2.25米;
(2)解:解方程,得,,
点坐标为,
.
故不计其他因素,水池的半径至少要2.5米,才能使喷出的水流不至于落在水池外.
19.(1)
(2)当时,有最大值,最大值是108
(3)能围成96平方米的面积,此时的长为4米或8米
【详解】(1)解:根据题意得:,
∴,
∴米,
则可表示为:,
故答案为:;
(2)解:根据题意得:,
∵,
∴当时,有最大值,最大值是108;
(3)能
∵,
∴,
∴,
∴或,
答:能围成96平方米的面积,此时的长为4米或8米.
20.(1),拱顶到地面的距离为米;(2)这辆货车不能安全通过,理由见解析;
(3)
【详解】(1)解:∵长方形的长是,宽是,
∴,,
代入,得:,解得:,
∴抛物线解析为,
∴顶点的坐标为;
∴拱顶到地面的距离为米;
(2)解:由(1)可知,抛物线的对称轴为直线,
∴货运汽车最外侧与地面的交点为或,
令或,得,
∴这辆货车不能安全通过;
(3)解:依题意,当时,,解得:
∴
∴两排灯的水平距离最小是米,
故答案为:.
21.(1);(2)元;(3)售价定为元可获得最大利润,最大利润是元
【详解】(1)解:设与之间的函数关系式为,
,解得,即与之间的函数表达式是;
(2)解:,解得,
∵尽量给客户优惠,
∴这种衬衫定价为元;
(3)解:由题意可得,
,
∵该衬衫的每件利润不允许高于进货价的,每件售价不低于进货价,
∴,,解得,
∴当时,取得最大值,此时,
答:售价定为元可获得最大利润,最大利润是元.
22.(1)小兵扔的小石头能击中点C,理由见解析
(2)
(3)小石头在运动过程中与直线的最大竖直距离为
【详解】(1)解:小兵扔的小石头能击中点C,理由如下:
∵根据题意,可得:抛物线的对称轴为,
又∵根据题意,可得:,,
∴点和点关于对称,
∴点在抛物线上,
∴小兵扔的小石头能击中点C;
(2)解:根据题意,可得:抛物线的顶点坐标为,
∴设抛物线的解析式为,
又∵点经过抛物线,
∴把的坐标代入解析式,可得:,解得:,
∴抛物线的解析式为,
又∵根据题意,可得:该抛物线的自变量的取值范围为,
∴小石头运动轨迹所在抛物线的解析式为,
(3)解:如图,连接,设直线的解析式为,
把代入,可得:,解得:,
∴直线的解析式为,
设直线上方的抛物线上的一点的坐标为,
过点作轴,交于点,则的坐标为,
∴,
∴当时,有最大值,最大值为,
∴小石头在运动过程中与直线的最大竖直距离为.
