2022-2023学年人教版数学七年级下册 5.1相交线同步练习(含答案)
文档属性
| 名称 | 2022-2023学年人教版数学七年级下册 5.1相交线同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 426.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-23 11:42:03 | ||
图片预览


文档简介
5.1相交线
(同步练习)
一、单选题
1.如图,下列说法错误的是( )
A.与是内错角 B.与是同位角
C.与是内错角 D.与是同旁内角
2.如图,是直线外一点,三点在直线上,且于点,,则下列结论中正确的是( )
①线段的长度是点到直线的距离;②线段是点到直线的距离;③在三条线段中,最短;④线段的长度是点到直线的距离
A.①②③ B.③④ C.①③ D.①②③④
3.如图中,∠1与∠2是对顶角的是( )
A. B.
C. D.
4.如图,直线AB与直线CD相交于点O,,,则∠AOC等于( )
A.55° B.65° C.75° D.115°
5.下列说法正确的个数是( )
①射线与射线是同一条射线;
②点到点的距离是线段;
③画一条长为的直线;
④在同一平面内,过一点有且只有一条直线垂直于已知直线.
A.0个 B.1个 C.2个 D.3个
6.下列四幅图中,∠1和∠2是同位角的是( )
A.⑴⑵ B.⑶⑷ C.⑴⑵⑶ D.⑵⑶⑷
7.如图,直线被所截,下列说法,正确的有( )
①与是同旁内角;
②与是内错角;
③与是同位角;
④与是内错角.
A.①③④ B.③④ C.①②④ D.①②③④
8.如图,点A到线段BC所在直线的距离是线段( )
A.AC的长度 B.AD的长度 C.AE的长度 D.AB的长度
9.如图两条平行线被第三条直线所截,其中互为内错角的是( )
A.∠1与∠2 B.∠4与∠2 C.∠1与∠3 D.∠3与∠2
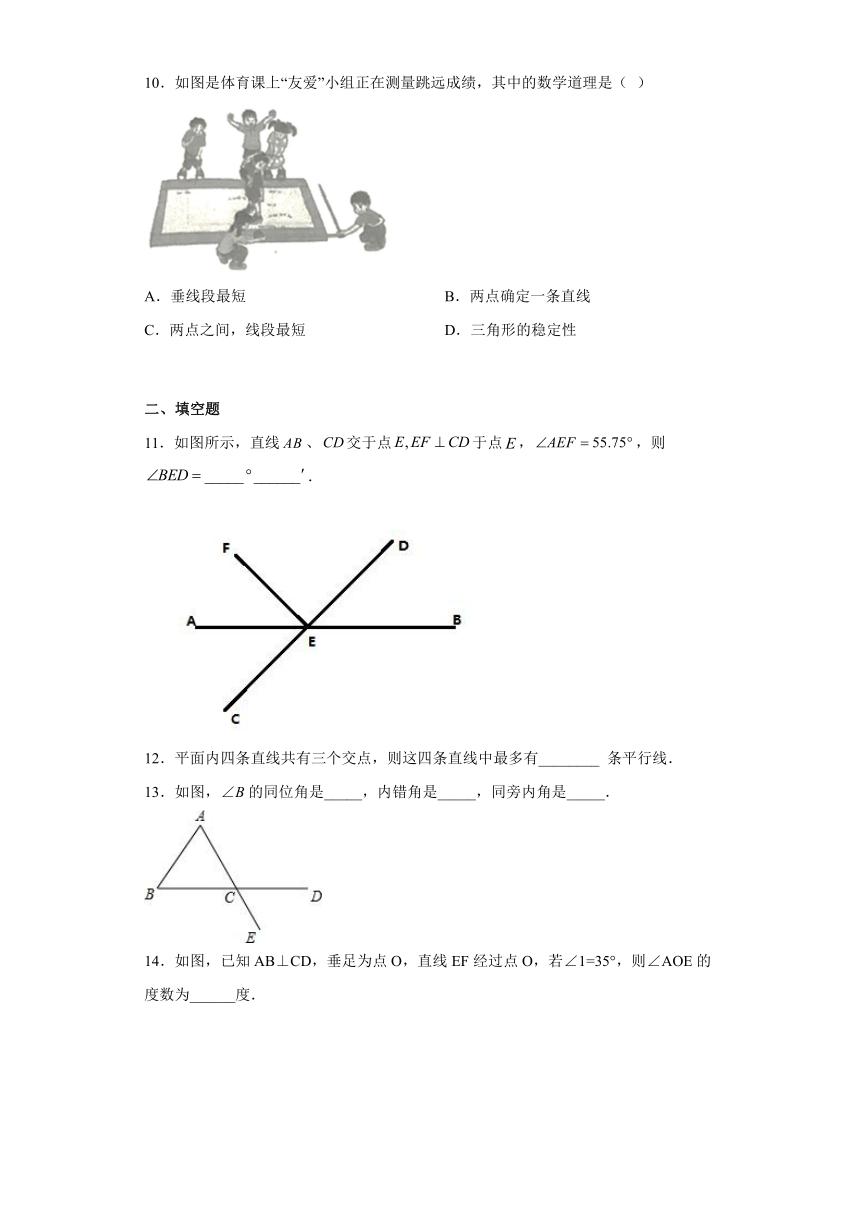
10.如图是体育课上“友爱”小组正在测量跳远成绩,其中的数学道理是( )
A.垂线段最短 B.两点确定一条直线
C.两点之间,线段最短 D.三角形的稳定性
二、填空题
11.如图所示,直线、交于点于点,,则.
12.平面内四条直线共有三个交点,则这四条直线中最多有________ 条平行线.
13.如图,∠B的同位角是_____,内错角是_____,同旁内角是_____.
14.如图,已知AB⊥CD,垂足为点O,直线EF经过点O,若∠1=35°,则∠AOE的度数为______度.
15.如图,按角的位置关系填空:∠A与∠2是_____.
三、解答题
16.如图,直线AB、CD交于点O,OE平分∠AOD,OF平分∠BOD.
(1)∠AOC=50°,求∠DOF与∠DOE的度数,并计算∠EOF的度数;
(2)当∠AOC的度数变化时,∠EOF的度数是否变化?若不变,求其值;若变化,说明理由.
17.已知,如图,AO⊥BC,DO⊥OE.
(1)在下面的横线上填上适当的角:
∠DOE=∠ +∠ ;∠BOE=∠ ﹣∠ ;
(2)不添加其它条件情况下,请尽可能多地写出图中有关角的等量关系(至少4个).
(3)如果∠COE=35°,求∠AOD的度数.
18.如图,平面上四个点A,B,C,D,按要求完成下列问题:
(1)画射线与直线相交于E点;
(2)在直线上找一点M,使线段最短,并说明理由.
19.如图,直线,相交于点,平分,,垂足为点.
(1)当时,求的度数;
(2)平分吗?为什么?
20.如图,直线,相交于点,射线平分,若,求的度数.
21.已知:如图,直线、相交于点O,平分, 于点O,且,
求:的度数.
参考答案:
1.A2.A3.B4.B5.B6.A7.D8.B9.A10.A
11.
12.三
13. ∠ACD; ∠BCE; ∠BAC和∠ACB
14.55
15.同旁内角
16.(1)由对顶角相等,得∠BOD=∠AOC=50°,
由OF平分∠BOD,得∠DOF=∠BOD=×50°=25°,
由邻补角互补,得∠AOD=180°-∠AOC=180°-50°=130°,
由OE平分∠AOD,得∠DOE=∠AOD=×130°=65°,
由角的和差,得∠EOF=∠DOF+∠DOE=25°+65°=90°;
(2)∠AOC的度数变化时,∠EOF的度数不变化,
由OF平分∠BOD,得∠DOF=∠BOD,
由OE平分∠AOD,得∠DOE=∠AOD,
由角的和差,得∠EOF=∠DOF+∠DOE=∠BOD+∠AOD=(∠AOD+∠BOD)=∠AOB=90°.
17.(1)∠DOA+∠AOE,∠BOC﹣∠COE.
(2)∠AOB=∠AOC,∠DOE=∠AOB,∠DOE=∠AOC,∠BOD=∠AOE,∠DOA=∠EOC.
(3)∠AOD=∠COE=35°.
18.解:(1)如图所示:
(2)如图所示:理由是垂线段最短.
19.解:(1)∵∠BOC=∠AOD=70°,
∵OE是∠COB的平分线,
∴∠BOE=∠BOC=35°.
(2)∵OE平分∠BOC,
∴∠BOE=∠COE,
∵OF⊥OE,
∴∠COE+∠COF=90°,∠BOE+∠AOF=90°,
∴∠BOE+∠COF=90°,
∴∠AOF=∠COF,
∴OF平分∠AOC.
20.
21..
(同步练习)
一、单选题
1.如图,下列说法错误的是( )
A.与是内错角 B.与是同位角
C.与是内错角 D.与是同旁内角
2.如图,是直线外一点,三点在直线上,且于点,,则下列结论中正确的是( )
①线段的长度是点到直线的距离;②线段是点到直线的距离;③在三条线段中,最短;④线段的长度是点到直线的距离
A.①②③ B.③④ C.①③ D.①②③④
3.如图中,∠1与∠2是对顶角的是( )
A. B.
C. D.
4.如图,直线AB与直线CD相交于点O,,,则∠AOC等于( )
A.55° B.65° C.75° D.115°
5.下列说法正确的个数是( )
①射线与射线是同一条射线;
②点到点的距离是线段;
③画一条长为的直线;
④在同一平面内,过一点有且只有一条直线垂直于已知直线.
A.0个 B.1个 C.2个 D.3个
6.下列四幅图中,∠1和∠2是同位角的是( )
A.⑴⑵ B.⑶⑷ C.⑴⑵⑶ D.⑵⑶⑷
7.如图,直线被所截,下列说法,正确的有( )
①与是同旁内角;
②与是内错角;
③与是同位角;
④与是内错角.
A.①③④ B.③④ C.①②④ D.①②③④
8.如图,点A到线段BC所在直线的距离是线段( )
A.AC的长度 B.AD的长度 C.AE的长度 D.AB的长度
9.如图两条平行线被第三条直线所截,其中互为内错角的是( )
A.∠1与∠2 B.∠4与∠2 C.∠1与∠3 D.∠3与∠2
10.如图是体育课上“友爱”小组正在测量跳远成绩,其中的数学道理是( )
A.垂线段最短 B.两点确定一条直线
C.两点之间,线段最短 D.三角形的稳定性
二、填空题
11.如图所示,直线、交于点于点,,则.
12.平面内四条直线共有三个交点,则这四条直线中最多有________ 条平行线.
13.如图,∠B的同位角是_____,内错角是_____,同旁内角是_____.
14.如图,已知AB⊥CD,垂足为点O,直线EF经过点O,若∠1=35°,则∠AOE的度数为______度.
15.如图,按角的位置关系填空:∠A与∠2是_____.
三、解答题
16.如图,直线AB、CD交于点O,OE平分∠AOD,OF平分∠BOD.
(1)∠AOC=50°,求∠DOF与∠DOE的度数,并计算∠EOF的度数;
(2)当∠AOC的度数变化时,∠EOF的度数是否变化?若不变,求其值;若变化,说明理由.
17.已知,如图,AO⊥BC,DO⊥OE.
(1)在下面的横线上填上适当的角:
∠DOE=∠ +∠ ;∠BOE=∠ ﹣∠ ;
(2)不添加其它条件情况下,请尽可能多地写出图中有关角的等量关系(至少4个).
(3)如果∠COE=35°,求∠AOD的度数.
18.如图,平面上四个点A,B,C,D,按要求完成下列问题:
(1)画射线与直线相交于E点;
(2)在直线上找一点M,使线段最短,并说明理由.
19.如图,直线,相交于点,平分,,垂足为点.
(1)当时,求的度数;
(2)平分吗?为什么?
20.如图,直线,相交于点,射线平分,若,求的度数.
21.已知:如图,直线、相交于点O,平分, 于点O,且,
求:的度数.
参考答案:
1.A2.A3.B4.B5.B6.A7.D8.B9.A10.A
11.
12.三
13. ∠ACD; ∠BCE; ∠BAC和∠ACB
14.55
15.同旁内角
16.(1)由对顶角相等,得∠BOD=∠AOC=50°,
由OF平分∠BOD,得∠DOF=∠BOD=×50°=25°,
由邻补角互补,得∠AOD=180°-∠AOC=180°-50°=130°,
由OE平分∠AOD,得∠DOE=∠AOD=×130°=65°,
由角的和差,得∠EOF=∠DOF+∠DOE=25°+65°=90°;
(2)∠AOC的度数变化时,∠EOF的度数不变化,
由OF平分∠BOD,得∠DOF=∠BOD,
由OE平分∠AOD,得∠DOE=∠AOD,
由角的和差,得∠EOF=∠DOF+∠DOE=∠BOD+∠AOD=(∠AOD+∠BOD)=∠AOB=90°.
17.(1)∠DOA+∠AOE,∠BOC﹣∠COE.
(2)∠AOB=∠AOC,∠DOE=∠AOB,∠DOE=∠AOC,∠BOD=∠AOE,∠DOA=∠EOC.
(3)∠AOD=∠COE=35°.
18.解:(1)如图所示:
(2)如图所示:理由是垂线段最短.
19.解:(1)∵∠BOC=∠AOD=70°,
∵OE是∠COB的平分线,
∴∠BOE=∠BOC=35°.
(2)∵OE平分∠BOC,
∴∠BOE=∠COE,
∵OF⊥OE,
∴∠COE+∠COF=90°,∠BOE+∠AOF=90°,
∴∠BOE+∠COF=90°,
∴∠AOF=∠COF,
∴OF平分∠AOC.
20.
21..
