2022—2023学年人教版数学八年级下册第16章 二次根式 复习练习(含答案)
文档属性
| 名称 | 2022—2023学年人教版数学八年级下册第16章 二次根式 复习练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 53.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-23 00:00:00 | ||
图片预览

文档简介
二次根式 章末复习
01分点突破
知识点1 二次式的概念及性质
1. 下列二次根式中, 属于最简二次根式的是( )
A. B. C. D.
2. 若xy<0,则 化简后的结果是( )
A. x B. x C. -x D. -x
3. 代数式 有意义时, x应满足的条件是 .
知识点2 二次根式的运算
4. 可以与 合并的二次根式是( )
A. B. C. D.
5. 下列运算中正确的是( )
A. B.
C. D.
6.计算:
(1) (2)
(3) (4)
知识点3 二次根式的实际应用
7. 如图, 长方形内有两个相邻的正方形, 其面积分别为2和8, 则图中阴影部分的面积为( )
A. B.2 C. D.6
02易错题集训
8. 下列计算正确的是( )
A. B. C. D.
9. 计算:÷× = .
10. 学习了二次根式的乘除后, 老师给同学们出了这样一道题: 已知a= ,求 的值, 黄梅想了想, 很快就算出来了,下面是她的解题过程:
解: ∵
又∵a=
∴
∴原式=.
你认为黄梅的解法对吗 如果对, 请你给他一句鼓励的话; 如果不对, 请找出错误的原因, 并改正
03常考题型演练
11. 下列计算正确的是( )
A. B. C. D.
12. 把-a 中根号外面的因式移到根号内的结果是( )
A. B. C. D.
13. 估计()× 的值应在( )
A.4和5之间 B.5和6之间 C.6和7之间 D.7和8之间
14. 计算: .
15. 当a>3时, 代数式 的值是 .
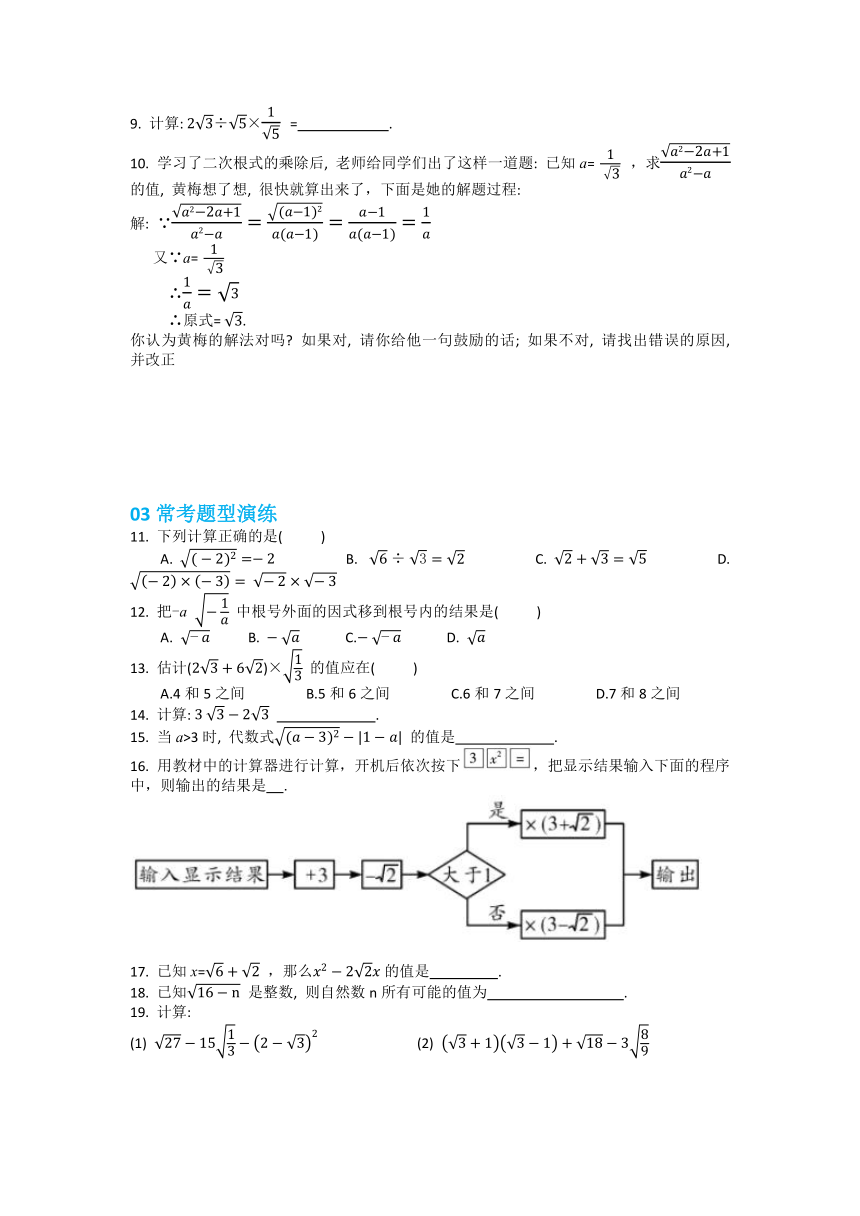
16. 用教材中的计算器进行计算,开机后依次按下,把显示结果输入下面的程序中,则输出的结果是 .
17. 已知x= ,那么的值是 .
18. 已知 是整数, 则自然数n所有可能的值为 .
19. 计算:
(1) (2)
20.已知x = , y = , 试求代数式3x2-5xy + 3y2的值
21. 教师节要到了, 为了表示对老师的敬意, 小明做了两张大小不同的正方形壁画准备送给老师, 其中一张面积为800 cm2, 另一张面积为450 cm2, 他想如果再用金彩带把壁画的边镶上会更漂亮, 他现在有1.2 m长的金彩带, 请你帮助算一算, 他的金彩带够用吗 如果不够, 还需买多长的金彩带 (≈1.414,结果保留整数)
22. 已知a,b,c满足|a -|+(c -)2=0
(1) 求a,b,c的值;
(2) 试问以a,b,c为边能否构成三角形 若能构成三角形, 请求出三角形的周长; 若不能,请说明理由
参考答案:
1.答案:B
2.答案:D
3. 答案: x>8
4.答案:C
5.答案:B
6.答案:(1) (2) (3) -5 (4)
7.答案:B
8. 答案:D
9. 答案:
10.解:不对;
∵a=<0,则a-1<0,
∴原式=,
将a= 代入,得原式=-。
11. 答案:B
12. 答案:A
13. 答案:C
14. 答案:
15. 答案:-2
16. 答案:34+9
由题意知输入的值为32=9
因为9+3-=12->1,
所以输出的结果为(12-)×(3+)= 34+9
17. 答案:4
18.答案:0,7,12,15,16
19.答案:(1)
(2)
20.解:3x2-5xy + 3y2=3(x-y) 2+ xy
将x = , y = , 代入上式,得:
3×() 2+()×()
=3×28+(-4)
=80
21. 解:正方形壁画的边长分别为 cm, cm.
镶壁画所用的金彩带长为4×(+ )=4×(20+15)=140≈197.96(cm).
因为1.2 m=120 cm<197.96 cm,
所以小明的金彩带不够用,197.96-120=77.96≈78(cm).
故还需买约78 cm长的金彩带.
22.解:(1) ∵|a -|+(c -)2=0
∴a - =0 ,=0 , c -=0
解得:a=,=5, c=3
(2) ∵+3=5>5
∴能构成三角形。
周长:+3+5=5+5
答:(1)a=,=5, c=3 。(2)能构成三角形,周长是(5+5)。
01分点突破
知识点1 二次式的概念及性质
1. 下列二次根式中, 属于最简二次根式的是( )
A. B. C. D.
2. 若xy<0,则 化简后的结果是( )
A. x B. x C. -x D. -x
3. 代数式 有意义时, x应满足的条件是 .
知识点2 二次根式的运算
4. 可以与 合并的二次根式是( )
A. B. C. D.
5. 下列运算中正确的是( )
A. B.
C. D.
6.计算:
(1) (2)
(3) (4)
知识点3 二次根式的实际应用
7. 如图, 长方形内有两个相邻的正方形, 其面积分别为2和8, 则图中阴影部分的面积为( )
A. B.2 C. D.6
02易错题集训
8. 下列计算正确的是( )
A. B. C. D.
9. 计算:÷× = .
10. 学习了二次根式的乘除后, 老师给同学们出了这样一道题: 已知a= ,求 的值, 黄梅想了想, 很快就算出来了,下面是她的解题过程:
解: ∵
又∵a=
∴
∴原式=.
你认为黄梅的解法对吗 如果对, 请你给他一句鼓励的话; 如果不对, 请找出错误的原因, 并改正
03常考题型演练
11. 下列计算正确的是( )
A. B. C. D.
12. 把-a 中根号外面的因式移到根号内的结果是( )
A. B. C. D.
13. 估计()× 的值应在( )
A.4和5之间 B.5和6之间 C.6和7之间 D.7和8之间
14. 计算: .
15. 当a>3时, 代数式 的值是 .
16. 用教材中的计算器进行计算,开机后依次按下,把显示结果输入下面的程序中,则输出的结果是 .
17. 已知x= ,那么的值是 .
18. 已知 是整数, 则自然数n所有可能的值为 .
19. 计算:
(1) (2)
20.已知x = , y = , 试求代数式3x2-5xy + 3y2的值
21. 教师节要到了, 为了表示对老师的敬意, 小明做了两张大小不同的正方形壁画准备送给老师, 其中一张面积为800 cm2, 另一张面积为450 cm2, 他想如果再用金彩带把壁画的边镶上会更漂亮, 他现在有1.2 m长的金彩带, 请你帮助算一算, 他的金彩带够用吗 如果不够, 还需买多长的金彩带 (≈1.414,结果保留整数)
22. 已知a,b,c满足|a -|+(c -)2=0
(1) 求a,b,c的值;
(2) 试问以a,b,c为边能否构成三角形 若能构成三角形, 请求出三角形的周长; 若不能,请说明理由
参考答案:
1.答案:B
2.答案:D
3. 答案: x>8
4.答案:C
5.答案:B
6.答案:(1) (2) (3) -5 (4)
7.答案:B
8. 答案:D
9. 答案:
10.解:不对;
∵a=<0,则a-1<0,
∴原式=,
将a= 代入,得原式=-。
11. 答案:B
12. 答案:A
13. 答案:C
14. 答案:
15. 答案:-2
16. 答案:34+9
由题意知输入的值为32=9
因为9+3-=12->1,
所以输出的结果为(12-)×(3+)= 34+9
17. 答案:4
18.答案:0,7,12,15,16
19.答案:(1)
(2)
20.解:3x2-5xy + 3y2=3(x-y) 2+ xy
将x = , y = , 代入上式,得:
3×() 2+()×()
=3×28+(-4)
=80
21. 解:正方形壁画的边长分别为 cm, cm.
镶壁画所用的金彩带长为4×(+ )=4×(20+15)=140≈197.96(cm).
因为1.2 m=120 cm<197.96 cm,
所以小明的金彩带不够用,197.96-120=77.96≈78(cm).
故还需买约78 cm长的金彩带.
22.解:(1) ∵|a -|+(c -)2=0
∴a - =0 ,=0 , c -=0
解得:a=,=5, c=3
(2) ∵+3=5>5
∴能构成三角形。
周长:+3+5=5+5
答:(1)a=,=5, c=3 。(2)能构成三角形,周长是(5+5)。
