2022—2023学年人教版数学七年级下册第九周不等式与不等式组 周测(含解析)
文档属性
| 名称 | 2022—2023学年人教版数学七年级下册第九周不等式与不等式组 周测(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 193.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-23 00:00:00 | ||
图片预览


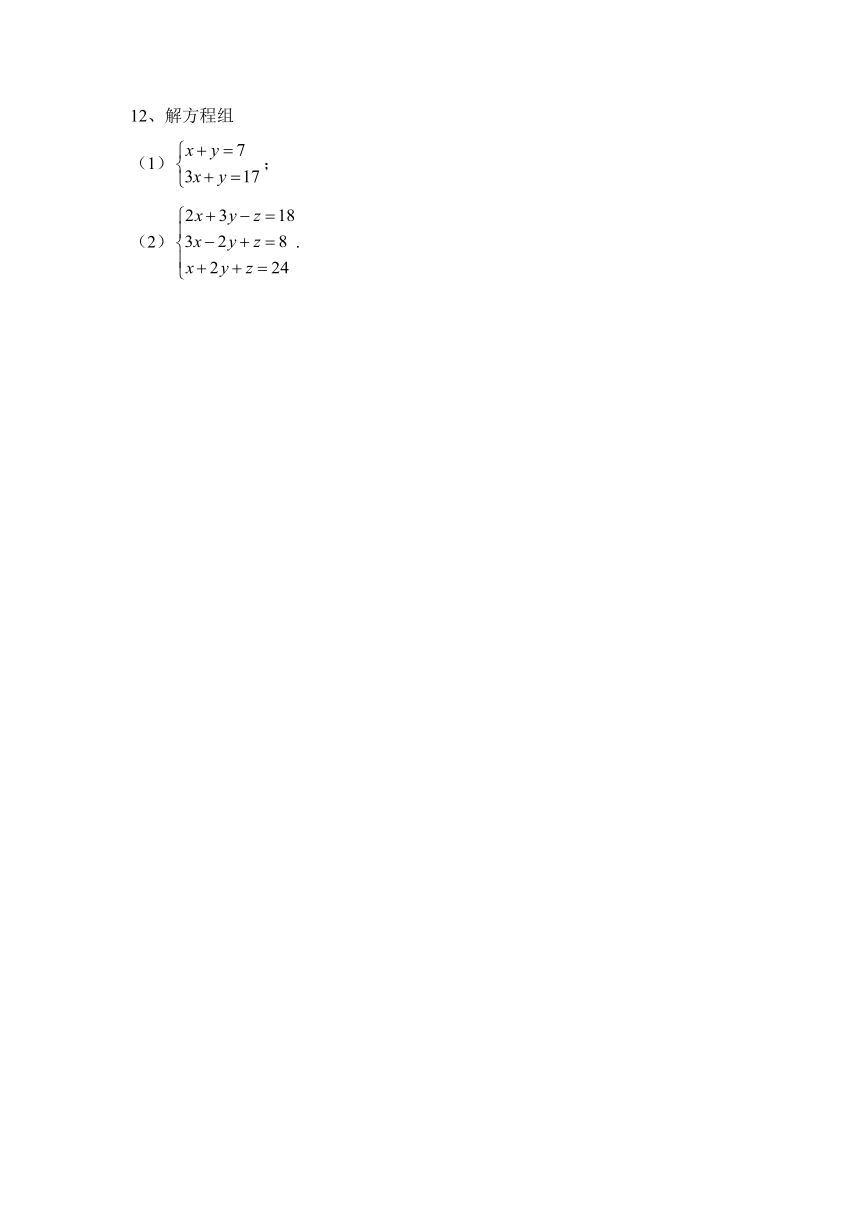
文档简介
第九周——2022-2023学年人教版数学七年级下册周周测
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1、我国古代数学名著《孙子算经》中记载:“今有木,不知长短,引绳度之,余绳四尺五寸;屈绳量之,不足一尺,木长几何?”意思是:用一根绳子去量一根木条,绳子还剩余4.5尺;将绳子对折再量木条,木条剩余1尺,问木条长多少尺?如果设木条长x尺,绳子长y尺,那么可列方程组为( )
A. B. C. D.
2、“绿水青山就是金山银山”,某地准备购买一些松树和柏树绿化荒山,已知购买2棵松树和3棵柏树需要120元,购买2棵松树比1棵柏树多20元,设每棵松树x元,每棵柏树y元,则列出的方程组正确的是( )
A. B.
C. D.
3、大约在1500年前成书的《孙子算经》中,记载了这样一个问题:“今有雏兔同笼,上有二十五头,下有七十六足,问雏兔各几何?”这四句话的意思是:有若干只鸡兔关在一个笼子里,从上面数,有25个头;从下面数,有76条腿,问笼中各有几只鸡和兔?设笼中有x只鸡y四只兔,则所列方程组正确的是( )
A. B. C. D.
4、如果方程组,的解使代数式的值为10,那么k的值为( )
A. B.3 C. D.
5、为培养青少年的创新意识、动手实践能力、现场应变能力和团队精神,湘潭市举办了第10届青少年机器人竞赛.组委会为每个比赛场地准备了四条腿的桌子和三条腿的凳子共12个,若桌子腿数与凳子腿数的和为40条,则每个比赛场地有几张桌子和几条凳子?设有x张桌子,有y条凳子,根据题意所列方程组正确的是( )
A. B. C. D.
6、将三元一次方程组,经过步骤和消去未知数z后,得到的二元一次方程组是( )
A. B. C. D.
7、如图,有一张边长为x的正方形ABCD纸板,在它的一个角上切去一个边长为y的正方形AEFG,剩下图形的面积是32,过点F作,垂足为H.将长方形GFHD切下,与长方形EBCH重新拼成一个长方形,若拼成的长方形的较长的一边长为8,则正方形ABCD的面积是( )
A.24 B.32 C.36 D.64
8、已知,则的值是( )
A.19 B.20 C.21 D.22
二、填空题
9、《九章算术》卷第七“盈不足”的第一十八个问题原文:今有黄金九枚,白银一十一枚,称之重适等.交易其一,金轻十三两.问金、银一枚各重几何?大致意思是:现有黄金9枚和白银11枚,它们的重量相等;互相交换1枚后,黄金8枚和白银1枚比白银10枚和黄金1枚轻13两.问金、银一枚各重多少?设每枚黄金重x两,每枚白银重y两,根据题意,列出的方程组是_________.
10、小红买书需用48元,付款时小红恰好用了1元和5元的纸币共12张,则小红所用的5元纸币为______张.
11、方程组的解为______.
三、解答题
12、解方程组
(1);
(2).
参考答案
1、答案:A
解析:由题知,木条长x尺,绳子长y尺,
由用一根绳子去量一根木条,绳子还剩余4.5尺,得:,
由将绳子对折再量木条,木条剩余1尺,得:,
故所求方程组为:,故选:A.
2、答案:A
解析:由题意,可列方程组为,
故选:A.
3、答案:A
解析:设笼中有x只鸡,y只兔,
根据题意得:,
故选:A.
4、答案:A
解析:
得④
得,解得,
将代入③得,解得,
将代入②得,解得,
解得
故选A.
5、答案:B
解析:组委会为每个比赛场地准备了桌子和凳子共12个,;又桌子腿数与凳子腿数的和为40条,且每张桌子有4条腿,每条凳子有3条腿,.列出的方程组为.故选:B.
6、答案:A
解析:,得,,得,得到的二元一次方程组是.
7、答案:C
解析:如图所示,
由已知得:,,
,
则,
解得:,
,
正方形ABCD的面积是36,
故选:C.
8、答案:C
解析:,
,
,解得
则
9、答案:(其他形式正确均可)
解析:设每枚黄金重x两,每枚白银重y两,
根据题意得:
10、答案:9
解析:设小红所用的1元纸币为x张,小红所用的5元纸币为y张,
,
解得:,
小红所用的1元纸币为3张,5元纸币为9张,
故答案为:9.
11、答案:
解析:由①可得:,然后代入②,与③一起联立成关于y和z的二元一次方程组,然后利用消元法求出方程组的解.
试题解析:,由①可得:④,将④代入②可得:,即⑤,⑤-③可得:,解得:;将代入①可得:;将代入③可得:;所以,原方程组的解为:.
12、答案:(1)
(2)
解析:方程组,
②-①得,即,
将代入①式,得,即,
所以方程组得解,
方程组,
①+②得,④
②-③得,⑤
④,⑤联立,得
利用代入消元法解得,,
将x与y代入①式得,所以,
所以方程组得解为.
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1、我国古代数学名著《孙子算经》中记载:“今有木,不知长短,引绳度之,余绳四尺五寸;屈绳量之,不足一尺,木长几何?”意思是:用一根绳子去量一根木条,绳子还剩余4.5尺;将绳子对折再量木条,木条剩余1尺,问木条长多少尺?如果设木条长x尺,绳子长y尺,那么可列方程组为( )
A. B. C. D.
2、“绿水青山就是金山银山”,某地准备购买一些松树和柏树绿化荒山,已知购买2棵松树和3棵柏树需要120元,购买2棵松树比1棵柏树多20元,设每棵松树x元,每棵柏树y元,则列出的方程组正确的是( )
A. B.
C. D.
3、大约在1500年前成书的《孙子算经》中,记载了这样一个问题:“今有雏兔同笼,上有二十五头,下有七十六足,问雏兔各几何?”这四句话的意思是:有若干只鸡兔关在一个笼子里,从上面数,有25个头;从下面数,有76条腿,问笼中各有几只鸡和兔?设笼中有x只鸡y四只兔,则所列方程组正确的是( )
A. B. C. D.
4、如果方程组,的解使代数式的值为10,那么k的值为( )
A. B.3 C. D.
5、为培养青少年的创新意识、动手实践能力、现场应变能力和团队精神,湘潭市举办了第10届青少年机器人竞赛.组委会为每个比赛场地准备了四条腿的桌子和三条腿的凳子共12个,若桌子腿数与凳子腿数的和为40条,则每个比赛场地有几张桌子和几条凳子?设有x张桌子,有y条凳子,根据题意所列方程组正确的是( )
A. B. C. D.
6、将三元一次方程组,经过步骤和消去未知数z后,得到的二元一次方程组是( )
A. B. C. D.
7、如图,有一张边长为x的正方形ABCD纸板,在它的一个角上切去一个边长为y的正方形AEFG,剩下图形的面积是32,过点F作,垂足为H.将长方形GFHD切下,与长方形EBCH重新拼成一个长方形,若拼成的长方形的较长的一边长为8,则正方形ABCD的面积是( )
A.24 B.32 C.36 D.64
8、已知,则的值是( )
A.19 B.20 C.21 D.22
二、填空题
9、《九章算术》卷第七“盈不足”的第一十八个问题原文:今有黄金九枚,白银一十一枚,称之重适等.交易其一,金轻十三两.问金、银一枚各重几何?大致意思是:现有黄金9枚和白银11枚,它们的重量相等;互相交换1枚后,黄金8枚和白银1枚比白银10枚和黄金1枚轻13两.问金、银一枚各重多少?设每枚黄金重x两,每枚白银重y两,根据题意,列出的方程组是_________.
10、小红买书需用48元,付款时小红恰好用了1元和5元的纸币共12张,则小红所用的5元纸币为______张.
11、方程组的解为______.
三、解答题
12、解方程组
(1);
(2).
参考答案
1、答案:A
解析:由题知,木条长x尺,绳子长y尺,
由用一根绳子去量一根木条,绳子还剩余4.5尺,得:,
由将绳子对折再量木条,木条剩余1尺,得:,
故所求方程组为:,故选:A.
2、答案:A
解析:由题意,可列方程组为,
故选:A.
3、答案:A
解析:设笼中有x只鸡,y只兔,
根据题意得:,
故选:A.
4、答案:A
解析:
得④
得,解得,
将代入③得,解得,
将代入②得,解得,
解得
故选A.
5、答案:B
解析:组委会为每个比赛场地准备了桌子和凳子共12个,;又桌子腿数与凳子腿数的和为40条,且每张桌子有4条腿,每条凳子有3条腿,.列出的方程组为.故选:B.
6、答案:A
解析:,得,,得,得到的二元一次方程组是.
7、答案:C
解析:如图所示,
由已知得:,,
,
则,
解得:,
,
正方形ABCD的面积是36,
故选:C.
8、答案:C
解析:,
,
,解得
则
9、答案:(其他形式正确均可)
解析:设每枚黄金重x两,每枚白银重y两,
根据题意得:
10、答案:9
解析:设小红所用的1元纸币为x张,小红所用的5元纸币为y张,
,
解得:,
小红所用的1元纸币为3张,5元纸币为9张,
故答案为:9.
11、答案:
解析:由①可得:,然后代入②,与③一起联立成关于y和z的二元一次方程组,然后利用消元法求出方程组的解.
试题解析:,由①可得:④,将④代入②可得:,即⑤,⑤-③可得:,解得:;将代入①可得:;将代入③可得:;所以,原方程组的解为:.
12、答案:(1)
(2)
解析:方程组,
②-①得,即,
将代入①式,得,即,
所以方程组得解,
方程组,
①+②得,④
②-③得,⑤
④,⑤联立,得
利用代入消元法解得,,
将x与y代入①式得,所以,
所以方程组得解为.
