6.1.3平方根 课件 (23张ppt)【人教版七下数学精品备课】
文档属性
| 名称 | 6.1.3平方根 课件 (23张ppt)【人教版七下数学精品备课】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-22 21:05:33 | ||
图片预览








文档简介
人教七下数学同步精品课件
人教版七年级下册
交流预习
2023春人教版七(下)数学同步精品课件
核心素养目标
复习引入
互助探究
例题精讲
跟踪训练
分层提高
课堂小结
知识自测
课后作业
6.1.3平方根
第六章 实数
核心素养目标:
掌握平方根的概念,明确平方根和算术平方根之间的联系和区别;
能用符号正确地表示一个数的平方根,理解开平方运算和乘方运算之间的互逆关系;
培养学生的探究能力和归纳问题的能力.
1.什么叫做算术平方根?
2.判断下列各数有没有算术平方根,如果有请
求出它们的算术平方根.
49;1; ; 0; -0.0025; (-3)2 ; -25;
复习引入:
若x2=????(x≥0),那么x叫做a的算术平方根。记作:x=????
?
49=7; 1=1; 36121=611; 0=0;
-0.0025没有算术平方根; ?32=3; -25没有算术平方根
?
问题 如果一个数的平方等于9,这个数是多少?
想一想:3和-3有什么特征?
由于 ,
所以这个数是3或-3.
互助探究:
根据上面的研究过程填表:
如果我们把 分别叫做
的平方根,你能给出平方根的概念吗?
互助探究:
例如:3和-3是9的平方根,简记为±3是9的平方根.
求一个数a的平方根的运算,叫做开平方
一、平方根的概念
新知讲解:
一般地,如果一个数的平方等于a,那么这个数叫做a的平方根或二次方根.这就是说,如果x2=a,那么x叫作a的平方根.
平方
开平方
新知讲解:
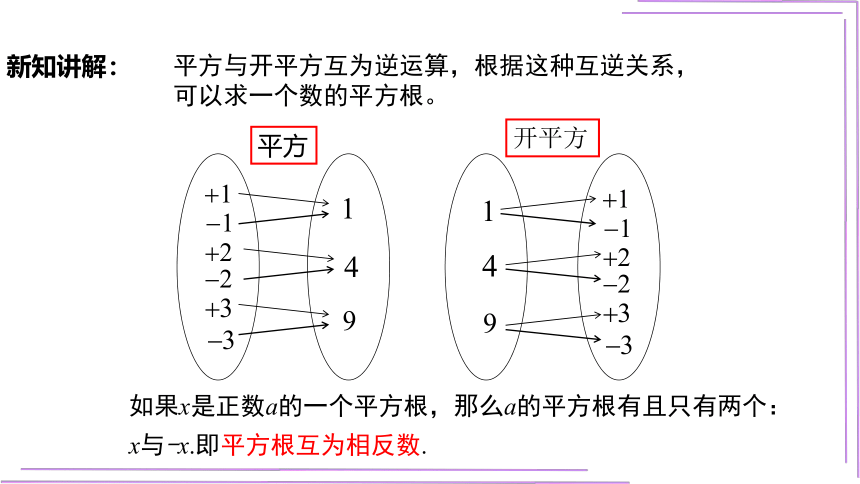
平方与开平方互为逆运算,根据这种互逆关系,可以求一个数的平方根。
如果x是正数a的一个平方根,那么a的平方根有且只有两个:x与-x.即平方根互为相反数.
例1 求下列各数的平方根:
(1)100; (2)916; (3)0.25.
解:(1)因为 ±102 =100 ,所以100的平方根是±10 ;
(2)因为 ±342 =916 ,所以916的平方根是±34;
(3)因为 ±0.52 =0.25 ,所以0.25的平方根是±0.5 ;
?
例题讲解:
互助探究:
思考:正数的平方根有什么特点?0的平方根是多少?负数有平方根吗?
我们发现,正数的平方根有两个,它们互为相反数,其中正的平方根就是这个数的算术平方根
因为02=0,并且任何一个不为0的平方都不等于0,所以0的平方根是0..
正数的平方根是正数,0的平方根是0,负数的平方根也是正数,即在我们所认识的数中,任何一个数的平方都不会是负数,所以负数没有平方根。
?
(1)正数的平方根有两个,它们互为相反数;
(2)0的平方根就是0 ;
(3)负数没有平方根.
二、平方根的性质:
新知讲解:
表示a的正的平方根
表示a的负的平方根
记作
a﹙a≥0﹚的平方根表示为
一个非负数的平方根的表示方法:
(算术平方根)
三、平方根的数学符号表示
新知讲解:
被开方数的取值范围:
只有a≥0时有意义,a<0时无意义.
例2 求下列各式的值:
解:(1) ;
(2) ;
(3) .
例题讲解:
教材46页练习
1. 判断下列说法是否正确.
正确.
(4)0.01是0.1的一个平方根。
(1)0的平方根是0;
(2)1的平方根是1;
(3)-1的平方根是-1;
不正确.
不正确.
不正确
跟踪练习:
跟踪练习:
x
8
-8
35
-35
4
-4
0.6
-0.6
????2
64
925
16
0.36
8
-8
4
-4
0.6
-0.6
64
16
0.36
教材46页练习
2. 填表
教材46页练习
3.计算下列各式的值:
(1)9; (2)?0.49; (3)±6481.
?
解:
(1)9 =3;
(2)?0.49=-0.7;
(3)±6481=±89
?
跟踪练习:
教材46页练习
4.平方根概念的起源与几何中的正方形有关,如果一个正方形的面积为A,那么这个正方形的边长是多少?
????
?
跟踪练习:
平方根
平方根的概念
开平方及相关运算
平方根的性质
课堂小结:
2
13
256
≥0
-5
互为相反数
课堂检测:
课后作业:
必做题:47页习题6.1第3、4题
选做题:48页习题6.1第8、9、10题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
人教版七年级下册
交流预习
2023春人教版七(下)数学同步精品课件
核心素养目标
复习引入
互助探究
例题精讲
跟踪训练
分层提高
课堂小结
知识自测
课后作业
6.1.3平方根
第六章 实数
核心素养目标:
掌握平方根的概念,明确平方根和算术平方根之间的联系和区别;
能用符号正确地表示一个数的平方根,理解开平方运算和乘方运算之间的互逆关系;
培养学生的探究能力和归纳问题的能力.
1.什么叫做算术平方根?
2.判断下列各数有没有算术平方根,如果有请
求出它们的算术平方根.
49;1; ; 0; -0.0025; (-3)2 ; -25;
复习引入:
若x2=????(x≥0),那么x叫做a的算术平方根。记作:x=????
?
49=7; 1=1; 36121=611; 0=0;
-0.0025没有算术平方根; ?32=3; -25没有算术平方根
?
问题 如果一个数的平方等于9,这个数是多少?
想一想:3和-3有什么特征?
由于 ,
所以这个数是3或-3.
互助探究:
根据上面的研究过程填表:
如果我们把 分别叫做
的平方根,你能给出平方根的概念吗?
互助探究:
例如:3和-3是9的平方根,简记为±3是9的平方根.
求一个数a的平方根的运算,叫做开平方
一、平方根的概念
新知讲解:
一般地,如果一个数的平方等于a,那么这个数叫做a的平方根或二次方根.这就是说,如果x2=a,那么x叫作a的平方根.
平方
开平方
新知讲解:
平方与开平方互为逆运算,根据这种互逆关系,可以求一个数的平方根。
如果x是正数a的一个平方根,那么a的平方根有且只有两个:x与-x.即平方根互为相反数.
例1 求下列各数的平方根:
(1)100; (2)916; (3)0.25.
解:(1)因为 ±102 =100 ,所以100的平方根是±10 ;
(2)因为 ±342 =916 ,所以916的平方根是±34;
(3)因为 ±0.52 =0.25 ,所以0.25的平方根是±0.5 ;
?
例题讲解:
互助探究:
思考:正数的平方根有什么特点?0的平方根是多少?负数有平方根吗?
我们发现,正数的平方根有两个,它们互为相反数,其中正的平方根就是这个数的算术平方根
因为02=0,并且任何一个不为0的平方都不等于0,所以0的平方根是0..
正数的平方根是正数,0的平方根是0,负数的平方根也是正数,即在我们所认识的数中,任何一个数的平方都不会是负数,所以负数没有平方根。
?
(1)正数的平方根有两个,它们互为相反数;
(2)0的平方根就是0 ;
(3)负数没有平方根.
二、平方根的性质:
新知讲解:
表示a的正的平方根
表示a的负的平方根
记作
a﹙a≥0﹚的平方根表示为
一个非负数的平方根的表示方法:
(算术平方根)
三、平方根的数学符号表示
新知讲解:
被开方数的取值范围:
只有a≥0时有意义,a<0时无意义.
例2 求下列各式的值:
解:(1) ;
(2) ;
(3) .
例题讲解:
教材46页练习
1. 判断下列说法是否正确.
正确.
(4)0.01是0.1的一个平方根。
(1)0的平方根是0;
(2)1的平方根是1;
(3)-1的平方根是-1;
不正确.
不正确.
不正确
跟踪练习:
跟踪练习:
x
8
-8
35
-35
4
-4
0.6
-0.6
????2
64
925
16
0.36
8
-8
4
-4
0.6
-0.6
64
16
0.36
教材46页练习
2. 填表
教材46页练习
3.计算下列各式的值:
(1)9; (2)?0.49; (3)±6481.
?
解:
(1)9 =3;
(2)?0.49=-0.7;
(3)±6481=±89
?
跟踪练习:
教材46页练习
4.平方根概念的起源与几何中的正方形有关,如果一个正方形的面积为A,那么这个正方形的边长是多少?
????
?
跟踪练习:
平方根
平方根的概念
开平方及相关运算
平方根的性质
课堂小结:
2
13
256
≥0
-5
互为相反数
课堂检测:
课后作业:
必做题:47页习题6.1第3、4题
选做题:48页习题6.1第8、9、10题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
