2023年河南省普通高中学业水平考试数学仿真模拟卷(四)(2月)(含解析)
文档属性
| 名称 | 2023年河南省普通高中学业水平考试数学仿真模拟卷(四)(2月)(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 198.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-23 07:37:09 | ||
图片预览



文档简介
河南省普通高中学业水平考试(2019版新教材)
数学仿真模拟卷(四)
一、选择题(本大题共16小题,每题3分,共48分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.已知集合A={x |x+1<0},B={x |x-3<0},那么集合A∪B等于( )
A.{x|-1≤x<3} B.{x |x<3} C.{x |x<-1} D.{ x |x>3}
2.已知a,b∈R,下列命题正确的是( )
A.若a>b,则|a|>|b| B.若a>b,则<
C.若|a|>b,则a2>b2 D.若a>|b|,则a2>b2
3.已知|a|=,|b|=2,a与b的夹角是120°,则a·b等于( )
A.3 B.-3 C.-3 D.3
4.某工厂甲、乙、丙三个车间生产了同一种产品,数量分别为120件,80件,60件.为了解它们的产品质量是否存在显著差异,用分层随机抽样方法抽取了一个容量为n的样本进行调查,其中从丙车间的产品中抽取了3件,则n等于( )
A.9 B.10 C.12 D.13
5.已知高为3的三棱柱ABC A1B1C1的底面是边长为1的正三角形,
如图所示,则三棱锥B1 ABC的体积为( )
A. B.
C. D.
6.以下数据为参加数学竞赛决赛的15人的成绩(单位:分):78,70,72,86,88,79,80,81,94,84,56,98,83,90,91,则这15人成绩的第80百分位数是( )
A.90 B.90.5 C.91 D.91.5
7.在△ABC中,若A=60°,B=45°,BC=3,则AC等于( )
A.4 B.2 C. D.
8.不等式≥0的解集为( )
A.{x|-19.已知函数f(2x+1)=3x+2,且f(a)=2,则a的值为( )
A.-1 B.5 C.1 D.8
10.设f(x)是定义在R上的奇函数,且当x≤0时,f(x)=x2-x,则f(1)=( )
A.- B.- C. D.
11.函数y=的定义域是( )
A.(-∞,0) B.(-∞,0] C.[0,+∞) D.(0,+∞)
12.函数y=x2-bx+1有一个零点,则b的值为( )
A.2 B.-2 C.±2 D.3
13.在△ABC中,a=7,b=4,c=,则△ABC的最小角为( )
A. B. C. D.
14.已知非零向量,不共线,且2=x+y,若=λ(λ∈R),则x,y满足的关系式是( )
A.x+y-2=0 B.2x+y-1=0 C.x+2y-2=0 D.2x+y-2=0
15.根据有关资料,围棋状态空间复杂度的上限M约为3361,而可观测宇宙中普通物质的原子总数N约为1080.则下列各数中与最接近的是(参考数据:lg 3≈0.48)( )
A.1033 B.1053 C.1073 D.1093
16.如图,正方形ABCD的边长为1,延长BA至E,使AE=1,连接EC,ED,则sin∠CED等于( )
A. B.
C. D.
二、填空题(本大题共7小题,每小题3分,共21分)
17.log5(log3(log2x))=0,则等于________.
18.已知z=m-1+(m+2)i在复平面内对应的点在第二象限,则实数m的取值范围是________.
19.某班全体学生参加物理测试成绩的频率分布直方图
如图所示,则估计该班物理测试的平均成绩是________分.
20.已知扇形的弧长是4 cm,面积是2 cm2,则扇形的圆心角的弧度数是________.
21.已知甲、乙、丙3名运动员击中目标的概率分别为0.7,0.8,0.85,且3人是否击中目标相互独立.若他们3人向目标各发1枪,则目标没有被击中的概率为________.
22.在矩形ABCD中,AB=1,BC=,PA⊥平面ABCD,PA=1,则PC与平面ABCD所成的角是________.
23.在平面直角坐标系中,以x轴的非负半轴为角的始边,如果角α,β的终边分别与单位圆交于点和,那么sin α·tan β=________.
三、解答题(本大题共6小题,共31分,解答应写出文字说明、证明过程或演算步骤)
24.先后抛掷两枚质地均匀的骰子.
(1)求点数之和为7的概率;
(2)求掷出两个4点的概率;
(3)求点数之和能被3整除的概率.
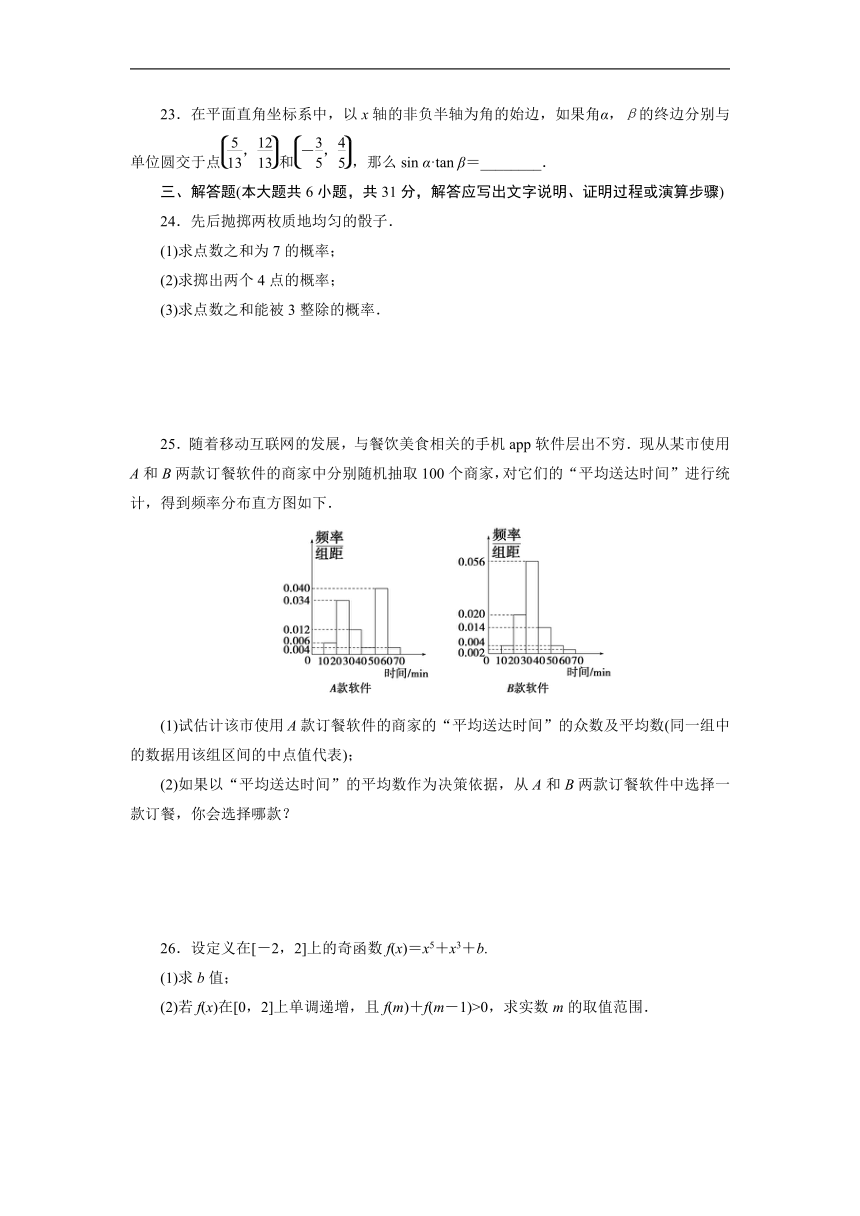
25.随着移动互联网的发展,与餐饮美食相关的手机app软件层出不穷.现从某市使用A和B两款订餐软件的商家中分别随机抽取100个商家,对它们的“平均送达时间”进行统计,得到频率分布直方图如下.
(1)试估计该市使用A款订餐软件的商家的“平均送达时间”的众数及平均数(同一组中的数据用该组区间的中点值代表);
(2)如果以“平均送达时间”的平均数作为决策依据,从A和B两款订餐软件中选择一款订餐,你会选择哪款?
26.设定义在[-2,2]上的奇函数f(x)=x5+x3+b.
(1)求b值;
(2)若f(x)在[0,2]上单调递增,且f(m)+f(m-1)>0,求实数m的取值范围.
27.已知函数f(x)=cos x+sin x+1.
(1)求函数f(x)的最小正周期;
(2)求函数f(x)的值域和单调递增区间.
28.如图,长方体ABCD A1B1C1D1的底面ABCD是正方形,点E在棱AA1上,BE⊥EC1.
(1)证明:BE⊥平面EB1C1;
(2)若AE=A1E,AB=3,求四棱锥E BB1C1C的体积.
29.在△ABC中,角A,B,C的对边分别为a,b,c,已知(a-c)(sin A+sin C)=(b-c)sin B.
(1)求角A的大小;
(2)若a=2bcos C,试判断△ABC的形状并给出证明.
仿真模拟卷(四)答案
1.解析:选B A={x|x+1<0}={x|x<-1},B={x|x-3<0}={x|x<3}.∴A∪B={x|x<3}.
2.解析:选D 当a=1,b=-2时,选项A、B、C均不正确;对于D项,a>|b|≥0,则a2>b2.
3.解析:选B 由数量积的定义,得a·b=|a||b|cos 120°=×2×=-3.
4.解析:选D ∵=,∴n=13.
5.解析:选D 设三棱锥B1 ABC的高为h,
则V三棱锥B1 ABC =S△ABCh=××3=.
6.解析:选B 把成绩按从小到大的顺序排列为
56,70,72,78,79,80,81,83,84,86,88,90,91,94,98,
因为15×80%=12,所以这15人成绩的第80百分位数是=90.5.
7.解析:选B 由正弦定理=,得=,所以AC=×=2.
8.解析:选B ∵原不等式
∴-1≤x<1,∴不等式的解集为{x|-1≤x<1}.
9.解析:选C 由3x+2=2得x=0,所以a=2×0+1=1.
10.解析:选A 因为f(x)是定义在R上的奇函数,所以f(1)=-f(-1)=-.
11.解析:选C 由2x-1≥0得2x≥1,即x≥0,∴函数的定义域为[0,+∞).
12.解析:选C 因为函数有一个零点,所以Δ=b2-4=0,所以b=±2.
13.解析:选B ∵a>b>c,∴C为最小角且C为锐角,
由余弦定理,得cos C===.
又∵C为锐角,∴C=,即△ABC的最小角为.
14.解析:选A 由=λ,得-=λ(-),即=(1+λ)-λ.又因为2=x+y,非零向量,不共线,
所以消去λ得x+y=2,即x+y-2=0.
15.解析:选D 由已知得,lg=lg M-lg N≈361×lg 3-80×lg 10≈361×0.48-80=93.28=lg 1093.28.故与最接近的是1093.
16.解析:选B 由题意知BC=1,BE=2,CE==,
sin∠BEC==,cos∠BEC==,
又因为∠CED=-∠BEC,
所以sin∠CED=sin
=sincos∠BEC-cossin∠BEC=×-×=.
17.解析:∵log5(log3(log2x))=0,∴log3(log2x)=1,
∴log2x=3,∴x=23=8.∴x-==.
答案:
18.解析:∵z=m-1+(m+2)i在复平面内对应的点在第二象限,∴m-1<0,且m+2>0,解得-2答案:(-2,1)
19.解析:平均成绩就是频率分布直方图中每个小矩形的面积乘以小矩形底边中点的横坐标再求和,即0.005×20×30+0.010×20×50+0.020×20×70+0.015×20×90=68(分).
答案:68
20.解析:因为扇形的弧长为4,面积为2,
所以扇形的面积为×4×r=2,解得r=1,则扇形的圆心角的弧度数为=4.
答案:4
21.解析:3人向目标各发1枪,由相互独立事件的概率计算公式,得目标没有被击中的概率P=(1-0.7)×(1-0.8)×(1-0.85)=0.3×0.2×0.15=0.009.
答案:0.009
22.解析:由题意知∠PCA为PC与平面ABCD所成的角,∵矩形ABCD中,AB=1,BC=,∴AC=,又∵PA=1,
∴在Rt△PAC中,tan∠PCA===,∴∠PCA=30°.
答案:30°
23.解析:由任意角的正弦、正切函数的定义知
sin α=,tan β==-,所以sin α·tan β=×=-.
答案:-
24.解:如图所示,从图中容易看出样本点与所描点一一对应,共36个,且每个样本点出现的可能性相等.
(1)记“点数之和为7”为事件A,从图中可以看出,事件A包含的样本点共有6个:(6,1),(5,2),(4,3),(3,4),(2,5),(1,6).
故P(A)==.
(2)记“掷出两个4点”为事件B,从图中可以看出,事件B包含的样本点只有1个,即(4,4).
故P(B)=.
(3)记“点数之和能被3整除”为事件C,则事件C包含的样本点共12个:(1,2),(2,1),(1,5),(5,1),(2,4),(4,2),(3,3),(3,6),(6,3),(4,5),(5,4),(6,6).
故P(C)==.
25.解:(1)依题意,可得使用A款订餐软件的商家中“平均送达时间”的众数为55,平均数为15×0.06+25×0.34+35×0.12+45×0.04+55×0.4+65×0.04=40.
(2)使用B款订餐软件的商家中“平均送达时间”的平均数为15×0.04+25×0.2+35×0.56+45×0.14+55×0.04+65×0.02=35<40,所以选B款订餐软件.
26.解:(1)因为函数f(x)是定义在[-2,2]上的奇函数,所以f(0)=0,解得b=0.
(2)因为函数f(x)在[0,2]上是增函数,又因为f(x)是奇函数,所以f(x)在[-2,2]上是单调递增的,
因为f(m)+f(m-1)>0,所以f(m-1)>-f(m)=f(-m),所以m-1>-m,①
又需要不等式f(m)+f(m-1)>0在函数f(x)定义域范围内有意义.
所以②
解①②得27.解:(1)因为f(x)=cos x+sin x+1,所以f(x)=2sin+1,
所以函数的最小正周期T==2π.
(2)因为sin∈[-1,1],
所以2sin+1∈[-1,3],即f(x)∈[-1,3].
令-+2kπ≤x+≤+2kπ(k∈Z),解得-+2kπ≤x≤+2kπ(k∈Z),
即函数的单调递增区间为(k∈Z).
28.(1)证明:由已知得B1C1⊥平面ABB1A1,BE 平面ABB1A1,
所以B1C1⊥BE.
又因为BE⊥EC1,B1C1∩EC1=C1,B1C1,EC1 平面EB1C1,
所以BE⊥平面EB1C1.
(2)解:由(1)知∠BEB1=90°.
由题设知Rt△ABE≌Rt△A1B1E,所以∠AEB=∠A1EB1=45°,
故AE=AB=3,AA1=2AE=6.
如图,作EF⊥BB1,垂足为F,则EF⊥平面BB1C1C,且EF=AB=3.
所以四棱锥E BB1C1C的体积V=×3×6×3=18.
29.(1)解:∵(a-c)(sin A+sin C)=(b-c)sin B,
∴由正弦定理得(a-c)(a+c)=(b-c)b,
∴=,根据余弦定理知cos A=.
又∵角A为△ABC的内角,∴A=.
(2)证明:△ABC为等边三角形.证明如下:
∵a=2bcos C,
∴由正弦定理得sin A=2sin Bcos C,
由三角形内角和公式得A=π-(B+C),
故sin A=sin(B+C),
∴sin(B+C)=2sin Bcos C,
即sin Bcos C+cos Bsin C=2sin Bcos C,
整理得sin Bcos C-cos Bsin C=0,
∴sin(B-C)=0,
又B-C∈(-π,π),∴B=C,
又由(1)知A=,∴△ABC为等边三角形.
数学仿真模拟卷(四)
一、选择题(本大题共16小题,每题3分,共48分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.已知集合A={x |x+1<0},B={x |x-3<0},那么集合A∪B等于( )
A.{x|-1≤x<3} B.{x |x<3} C.{x |x<-1} D.{ x |x>3}
2.已知a,b∈R,下列命题正确的是( )
A.若a>b,则|a|>|b| B.若a>b,则<
C.若|a|>b,则a2>b2 D.若a>|b|,则a2>b2
3.已知|a|=,|b|=2,a与b的夹角是120°,则a·b等于( )
A.3 B.-3 C.-3 D.3
4.某工厂甲、乙、丙三个车间生产了同一种产品,数量分别为120件,80件,60件.为了解它们的产品质量是否存在显著差异,用分层随机抽样方法抽取了一个容量为n的样本进行调查,其中从丙车间的产品中抽取了3件,则n等于( )
A.9 B.10 C.12 D.13
5.已知高为3的三棱柱ABC A1B1C1的底面是边长为1的正三角形,
如图所示,则三棱锥B1 ABC的体积为( )
A. B.
C. D.
6.以下数据为参加数学竞赛决赛的15人的成绩(单位:分):78,70,72,86,88,79,80,81,94,84,56,98,83,90,91,则这15人成绩的第80百分位数是( )
A.90 B.90.5 C.91 D.91.5
7.在△ABC中,若A=60°,B=45°,BC=3,则AC等于( )
A.4 B.2 C. D.
8.不等式≥0的解集为( )
A.{x|-1
A.-1 B.5 C.1 D.8
10.设f(x)是定义在R上的奇函数,且当x≤0时,f(x)=x2-x,则f(1)=( )
A.- B.- C. D.
11.函数y=的定义域是( )
A.(-∞,0) B.(-∞,0] C.[0,+∞) D.(0,+∞)
12.函数y=x2-bx+1有一个零点,则b的值为( )
A.2 B.-2 C.±2 D.3
13.在△ABC中,a=7,b=4,c=,则△ABC的最小角为( )
A. B. C. D.
14.已知非零向量,不共线,且2=x+y,若=λ(λ∈R),则x,y满足的关系式是( )
A.x+y-2=0 B.2x+y-1=0 C.x+2y-2=0 D.2x+y-2=0
15.根据有关资料,围棋状态空间复杂度的上限M约为3361,而可观测宇宙中普通物质的原子总数N约为1080.则下列各数中与最接近的是(参考数据:lg 3≈0.48)( )
A.1033 B.1053 C.1073 D.1093
16.如图,正方形ABCD的边长为1,延长BA至E,使AE=1,连接EC,ED,则sin∠CED等于( )
A. B.
C. D.
二、填空题(本大题共7小题,每小题3分,共21分)
17.log5(log3(log2x))=0,则等于________.
18.已知z=m-1+(m+2)i在复平面内对应的点在第二象限,则实数m的取值范围是________.
19.某班全体学生参加物理测试成绩的频率分布直方图
如图所示,则估计该班物理测试的平均成绩是________分.
20.已知扇形的弧长是4 cm,面积是2 cm2,则扇形的圆心角的弧度数是________.
21.已知甲、乙、丙3名运动员击中目标的概率分别为0.7,0.8,0.85,且3人是否击中目标相互独立.若他们3人向目标各发1枪,则目标没有被击中的概率为________.
22.在矩形ABCD中,AB=1,BC=,PA⊥平面ABCD,PA=1,则PC与平面ABCD所成的角是________.
23.在平面直角坐标系中,以x轴的非负半轴为角的始边,如果角α,β的终边分别与单位圆交于点和,那么sin α·tan β=________.
三、解答题(本大题共6小题,共31分,解答应写出文字说明、证明过程或演算步骤)
24.先后抛掷两枚质地均匀的骰子.
(1)求点数之和为7的概率;
(2)求掷出两个4点的概率;
(3)求点数之和能被3整除的概率.
25.随着移动互联网的发展,与餐饮美食相关的手机app软件层出不穷.现从某市使用A和B两款订餐软件的商家中分别随机抽取100个商家,对它们的“平均送达时间”进行统计,得到频率分布直方图如下.
(1)试估计该市使用A款订餐软件的商家的“平均送达时间”的众数及平均数(同一组中的数据用该组区间的中点值代表);
(2)如果以“平均送达时间”的平均数作为决策依据,从A和B两款订餐软件中选择一款订餐,你会选择哪款?
26.设定义在[-2,2]上的奇函数f(x)=x5+x3+b.
(1)求b值;
(2)若f(x)在[0,2]上单调递增,且f(m)+f(m-1)>0,求实数m的取值范围.
27.已知函数f(x)=cos x+sin x+1.
(1)求函数f(x)的最小正周期;
(2)求函数f(x)的值域和单调递增区间.
28.如图,长方体ABCD A1B1C1D1的底面ABCD是正方形,点E在棱AA1上,BE⊥EC1.
(1)证明:BE⊥平面EB1C1;
(2)若AE=A1E,AB=3,求四棱锥E BB1C1C的体积.
29.在△ABC中,角A,B,C的对边分别为a,b,c,已知(a-c)(sin A+sin C)=(b-c)sin B.
(1)求角A的大小;
(2)若a=2bcos C,试判断△ABC的形状并给出证明.
仿真模拟卷(四)答案
1.解析:选B A={x|x+1<0}={x|x<-1},B={x|x-3<0}={x|x<3}.∴A∪B={x|x<3}.
2.解析:选D 当a=1,b=-2时,选项A、B、C均不正确;对于D项,a>|b|≥0,则a2>b2.
3.解析:选B 由数量积的定义,得a·b=|a||b|cos 120°=×2×=-3.
4.解析:选D ∵=,∴n=13.
5.解析:选D 设三棱锥B1 ABC的高为h,
则V三棱锥B1 ABC =S△ABCh=××3=.
6.解析:选B 把成绩按从小到大的顺序排列为
56,70,72,78,79,80,81,83,84,86,88,90,91,94,98,
因为15×80%=12,所以这15人成绩的第80百分位数是=90.5.
7.解析:选B 由正弦定理=,得=,所以AC=×=2.
8.解析:选B ∵原不等式
∴-1≤x<1,∴不等式的解集为{x|-1≤x<1}.
9.解析:选C 由3x+2=2得x=0,所以a=2×0+1=1.
10.解析:选A 因为f(x)是定义在R上的奇函数,所以f(1)=-f(-1)=-.
11.解析:选C 由2x-1≥0得2x≥1,即x≥0,∴函数的定义域为[0,+∞).
12.解析:选C 因为函数有一个零点,所以Δ=b2-4=0,所以b=±2.
13.解析:选B ∵a>b>c,∴C为最小角且C为锐角,
由余弦定理,得cos C===.
又∵C为锐角,∴C=,即△ABC的最小角为.
14.解析:选A 由=λ,得-=λ(-),即=(1+λ)-λ.又因为2=x+y,非零向量,不共线,
所以消去λ得x+y=2,即x+y-2=0.
15.解析:选D 由已知得,lg=lg M-lg N≈361×lg 3-80×lg 10≈361×0.48-80=93.28=lg 1093.28.故与最接近的是1093.
16.解析:选B 由题意知BC=1,BE=2,CE==,
sin∠BEC==,cos∠BEC==,
又因为∠CED=-∠BEC,
所以sin∠CED=sin
=sincos∠BEC-cossin∠BEC=×-×=.
17.解析:∵log5(log3(log2x))=0,∴log3(log2x)=1,
∴log2x=3,∴x=23=8.∴x-==.
答案:
18.解析:∵z=m-1+(m+2)i在复平面内对应的点在第二象限,∴m-1<0,且m+2>0,解得-2
19.解析:平均成绩就是频率分布直方图中每个小矩形的面积乘以小矩形底边中点的横坐标再求和,即0.005×20×30+0.010×20×50+0.020×20×70+0.015×20×90=68(分).
答案:68
20.解析:因为扇形的弧长为4,面积为2,
所以扇形的面积为×4×r=2,解得r=1,则扇形的圆心角的弧度数为=4.
答案:4
21.解析:3人向目标各发1枪,由相互独立事件的概率计算公式,得目标没有被击中的概率P=(1-0.7)×(1-0.8)×(1-0.85)=0.3×0.2×0.15=0.009.
答案:0.009
22.解析:由题意知∠PCA为PC与平面ABCD所成的角,∵矩形ABCD中,AB=1,BC=,∴AC=,又∵PA=1,
∴在Rt△PAC中,tan∠PCA===,∴∠PCA=30°.
答案:30°
23.解析:由任意角的正弦、正切函数的定义知
sin α=,tan β==-,所以sin α·tan β=×=-.
答案:-
24.解:如图所示,从图中容易看出样本点与所描点一一对应,共36个,且每个样本点出现的可能性相等.
(1)记“点数之和为7”为事件A,从图中可以看出,事件A包含的样本点共有6个:(6,1),(5,2),(4,3),(3,4),(2,5),(1,6).
故P(A)==.
(2)记“掷出两个4点”为事件B,从图中可以看出,事件B包含的样本点只有1个,即(4,4).
故P(B)=.
(3)记“点数之和能被3整除”为事件C,则事件C包含的样本点共12个:(1,2),(2,1),(1,5),(5,1),(2,4),(4,2),(3,3),(3,6),(6,3),(4,5),(5,4),(6,6).
故P(C)==.
25.解:(1)依题意,可得使用A款订餐软件的商家中“平均送达时间”的众数为55,平均数为15×0.06+25×0.34+35×0.12+45×0.04+55×0.4+65×0.04=40.
(2)使用B款订餐软件的商家中“平均送达时间”的平均数为15×0.04+25×0.2+35×0.56+45×0.14+55×0.04+65×0.02=35<40,所以选B款订餐软件.
26.解:(1)因为函数f(x)是定义在[-2,2]上的奇函数,所以f(0)=0,解得b=0.
(2)因为函数f(x)在[0,2]上是增函数,又因为f(x)是奇函数,所以f(x)在[-2,2]上是单调递增的,
因为f(m)+f(m-1)>0,所以f(m-1)>-f(m)=f(-m),所以m-1>-m,①
又需要不等式f(m)+f(m-1)>0在函数f(x)定义域范围内有意义.
所以②
解①②得
所以函数的最小正周期T==2π.
(2)因为sin∈[-1,1],
所以2sin+1∈[-1,3],即f(x)∈[-1,3].
令-+2kπ≤x+≤+2kπ(k∈Z),解得-+2kπ≤x≤+2kπ(k∈Z),
即函数的单调递增区间为(k∈Z).
28.(1)证明:由已知得B1C1⊥平面ABB1A1,BE 平面ABB1A1,
所以B1C1⊥BE.
又因为BE⊥EC1,B1C1∩EC1=C1,B1C1,EC1 平面EB1C1,
所以BE⊥平面EB1C1.
(2)解:由(1)知∠BEB1=90°.
由题设知Rt△ABE≌Rt△A1B1E,所以∠AEB=∠A1EB1=45°,
故AE=AB=3,AA1=2AE=6.
如图,作EF⊥BB1,垂足为F,则EF⊥平面BB1C1C,且EF=AB=3.
所以四棱锥E BB1C1C的体积V=×3×6×3=18.
29.(1)解:∵(a-c)(sin A+sin C)=(b-c)sin B,
∴由正弦定理得(a-c)(a+c)=(b-c)b,
∴=,根据余弦定理知cos A=.
又∵角A为△ABC的内角,∴A=.
(2)证明:△ABC为等边三角形.证明如下:
∵a=2bcos C,
∴由正弦定理得sin A=2sin Bcos C,
由三角形内角和公式得A=π-(B+C),
故sin A=sin(B+C),
∴sin(B+C)=2sin Bcos C,
即sin Bcos C+cos Bsin C=2sin Bcos C,
整理得sin Bcos C-cos Bsin C=0,
∴sin(B-C)=0,
又B-C∈(-π,π),∴B=C,
又由(1)知A=,∴△ABC为等边三角形.
同课章节目录
