2014学年度大庆市房顶中学第二学期初二数学第一次月考试题解析与参考答案
文档属性
| 名称 | 2014学年度大庆市房顶中学第二学期初二数学第一次月考试题解析与参考答案 |  | |
| 格式 | zip | ||
| 文件大小 | 205.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-03-31 11:28:21 | ||
图片预览



文档简介
2014学年度第二学期初二数学第一次月考
一.选择题(共12小题)
1. 的平方根是( )
A. 3 B. ±3 C. D. ±
2.下列运算正确的是( )
A. a2 a3=a6 B. +=2+ C.(x﹣2)(x+3)=x2﹣6 D.(﹣a)2=﹣a2
3.如图,A、B两点在数轴上表示的数分别是a、b,则下列式子中成立的是( )
A.a+b<0 B.﹣a<﹣b C.1﹣2a>1﹣2b D.|a|﹣|b|>0
4.如图,将△ABC绕点A逆时针旋转一定角度,得到△ADE.若∠CAE=65°,∠E=70°,且AD⊥BC,∠BAC的度数为( )
A. 60° B. 75° C. 85° D. 90°
4题 5题 8题
5.在6×6方格中,将图1中的图形N平移后位置如图2所示,则图形N的平移方法中,正确的是)
A. 向下移动1格 B. 向上移动1格 C. 向上移动2格 D. 向下移动2格
6.一直角三角形的两边长分别为3和4.则第三边的长为( )
A. 5 B. C. D. 5或
7.将一等腰直角三角形纸片对折后再对折,得到如图所示的图形,然后将阴影部分剪掉,把剩余部分展开后的平面图形是( )
A. B. C. D.
8.如图,有两颗树,一颗高10米,另一颗高4米,两树相距8米.一只鸟从一颗树的树梢飞到另一颗树的树梢,问小鸟至少飞行( )
A. 8米 B. 10米 C. 12米 D. 14米
9.在面积为15的平行四边形ABCD中,过点A作AE垂直于直线BC于点E,作AF垂直于直线CD于点F,若AB=5,BC=6,则CE+CF的值为( )
A. 11+ B. 11﹣ C. 11+或11﹣ D. 11+或1+
10.下列图形中,既是轴对称图形又是中心对称图形的有( )
A. 4个 B. 3个 C. 2个 D. 1个
10题 11题
11.如图,直角梯形ABCD中,AB∥CD,∠C=90°,∠BDA=90°,AB=a,BD=b,CD=c,BC=d,AD=e,则下列等式成立的是( )
A. b2=ac B. b2=ce C. be=ac D. bd=ae
12.在如图所示的单位正方形网格中,△ABC经过平移后得到△A1B1C1,已知在AC上一点P(2.4,2)平移后的对应点为P1,点P1绕点O逆时针旋转180°,得到对应点P2,则P2点的坐标为( )
A. (1.4,﹣1) B. (1.5,2) C. (1.6,1) D. (2.4,1)
二.填空题(共6小题)
13.如图,AC⊥CD,垂足为点C,BD⊥CD,垂足为点D,AB与CD交于点O.若AC=1,BD=2,CD=4,则AB= _________ .
12题 13题 17题
14.等腰三角形一腰长为5,一边上的高为4,则底边长 _________ .
15.已知实数x,y满足,则以x,y的值为两边长的等腰三角形的周长是 ____ .
16.已知a、b为两个连续整数,且a<<b,则a+b= _________ .
17.如图,把△PQR沿着PQ的方向平移到△P′Q′R′的位置,它们重叠部分的面积是△PQR面积的一半,若PQ=,则此三角形移动的距离PP′= _________ .
18.分析图①,②,④中阴影部分的分布规律,按此规律在图③中画出其中的阴影部分 _________ .
三.解答题(共10小题)
19.计算:|﹣2|+.
20.已知:,求的值.
21.计算:.
22.先化简,再求值.,其中x=1,y=.
23.已知:,求的值.
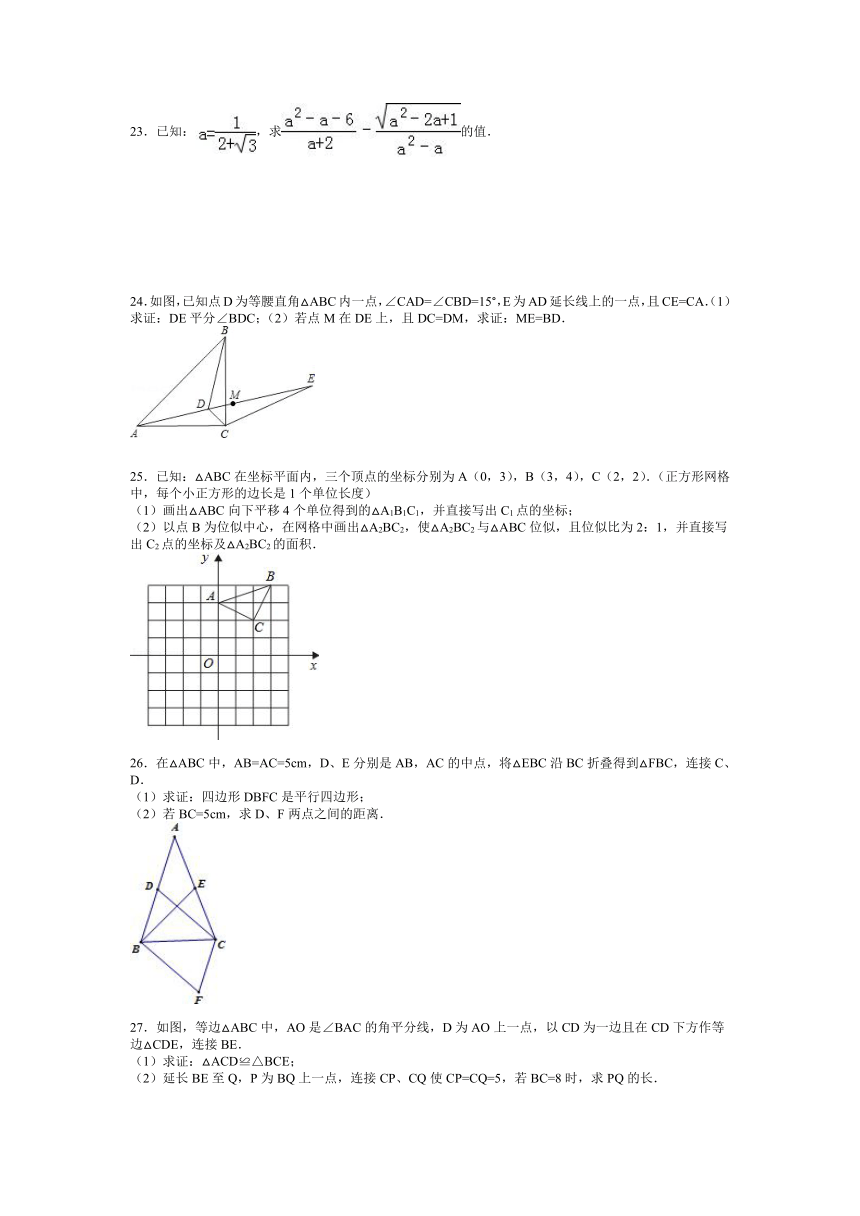
24.如图,已知点D为等腰直角△ABC内一点,∠CAD=∠CBD=15°,E为AD延长线上的一点,且CE=CA.(1)求证:DE平分∠BDC;(2)若点M在DE上,且DC=DM,求证:ME=BD.
25.已知:△ABC在坐标平面内,三个顶点的坐标分别为A(0,3),B(3,4),C(2,2).(正方形网格中,每个小正方形的边长是1个单位长度)
(1)画出△ABC向下平移4个单位得到的△A1B1C1,并直接写出C1点的坐标;
(2)以点B为位似中心,在网格中画出△A2BC2,使△A2BC2与△ABC位似,且位似比为2:1,并直接写出C2点的坐标及△A2BC2的面积.
26.在△ABC中,AB=AC=5cm,D、E分别是AB,AC的中点,将△EBC沿BC折叠得到△FBC,连接C、D.
(1)求证:四边形DBFC是平行四边形;
(2)若BC=5cm,求D、F两点之间的距离.
27.如图,等边△ABC中,AO是∠BAC的角平分线,D为AO上一点,以CD为一边且在CD下方作等边△CDE,连接BE.
(1)求证:△ACD≌△BCE;
(2)延长BE至Q,P为BQ上一点,连接CP、CQ使CP=CQ=5,若BC=8时,求PQ的长.
2014学年度大庆市房顶中学第二学期初二数学第一次月考
参考答案与试题解析
一.选择题(共12小题)
1.D
2.B
3.C
4.C
5.D
6.D
7.A
8.B
9.D
10.B
11.A
12.C
二.填空题(共6小题)
13. 5 .
14. 6或2或4 .
15. 20 .
16. 9 .
17.
18.见答图
三.解答题(共10小题)
19.计算:|﹣2|+.
解答: 解:原式=2+1×1﹣2+
=.
20.已知:,求的值.
解答: 解:∵a=,
=2﹣,
∴a<1,
∴原式=
=,
=,
=﹣2﹣.
21.计算:.
解答: 解:原式=,
=,
=,
=
22.先化简,再求值.,其中x=1,y=.
解答: 解:原式=,
=,
=﹣,
=0.
当x=1,y=时,原式=0.
23.已知:,求的值.
解答: 解:∵a==2﹣<1,
∴原式==a﹣3+
=2﹣﹣3+2+=1.
24.如图,已知点D为等腰直角△ABC内一点,∠CAD=∠CBD=15°,E为AD延长线上的一点,且CE=CA.
(1)求证:DE平分∠BDC;
(2)若点M在DE上,且DC=DM,求证:ME=BD.
解答: 证明:(1)∵△ABC是等腰直角三角形,
∴∠BAC=∠ABC=45°,
∵∠CAD=∠CBD=15°,
∴∠BAD=∠ABD=45°﹣15°=30°,
∴BD=AD,
∴D在AB的垂直平分线上,
∵AC=BC,
∴C也在AB的垂直平分线上,
即直线CD是AB的垂直平分线,
∴∠ACD=∠BCD=45°,
∴∠CDE=15°+45°=60°,
∴∠BDE=∠DBA+∠BAD=60°;
∴∠CDE=∠BDE,
即DE平分∠BDC.
(2)如图,连接MC.
∵DC=DM,且∠MDC=60°,
∴△MDC是等边三角形,即CM=CD.∠DMC=∠MDC=60°,
∵∠ADC+∠MDC=180°,∠DMC+∠EMC=180°,
∴∠EMC=∠ADC.
又∵CE=CA,
∴∠DAC=∠CEM.
在△ADC与△EMC中,
,
∴△ADC≌△EMC(AAS),
∴ME=AD=BD.
25.已知:△ABC在坐标平面内,三个顶点的坐标分别为A(0,3),B(3,4),C(2,2).(正方形网格中,每个小正方形的边长是1个单位长度)
(1)画出△ABC向下平移4个单位得到的△A1B1C1,并直接写出C1点的坐标;
(2)以点B为位似中心,在网格中画出△A2BC2,使△A2BC2与△ABC位似,且位似比为2:1,并直接写出C2点的坐标及△A2BC2的面积.
解答: 解:(1)如图,△A1B1C1即为所求,C1(2,﹣2);
(2)如图,△A2BC2即为所求,C2(1,0),
△A2BC2的面积:
6×4﹣×2×6﹣×2×4﹣×2×4
=24﹣6﹣4﹣4
=24﹣14
=10.
26.在△ABC中,AB=AC=5cm,D、E分别是AB,AC的中点,将△EBC沿BC折叠得到△FBC,连接C、D.
(1)求证:四边形DBFC是平行四边形;
(2)若BC=5cm,求D、F两点之间的距离.
解答: (1)证明:∵AB=AC=5cm,D、E分别是AB,AC的中点,
∴BD=CE=2.5cm,∠ABC=∠ACB,BC=BC,
∴△BEC≌△CDB,
∴BE=CD,
∵△BFC是△BEC翻折而成,
∴BE=BF,CE=CF,
∴BF=CD,CF=BD,
∴四边形DBFC是平行四边形;
(2)解:连接DF,
∵AB=AC=5cm,BC=5cm,
∴△ABC是等边三角形,
∵D是AB的中点,
∴CD⊥AB,∠BCD=30°,
∴CD=BC cos30°=5×=,
∴四边形DBFC是矩形,
∴BF=CD=
在Rt△BDF中,
DF===5cm.
27.如图,等边△ABC中,AO是∠BAC的角平分线,D为AO上一点,以CD为一边且在CD下方作等边△CDE,连接BE.
(1)求证:△ACD≌△BCE;
(2)延长BE至Q,P为BQ上一点,连接CP、CQ使CP=CQ=5,若BC=8时,求PQ的长.
解答: (1)证明:∵△ABC与△DCE是等边三角形,
∴AC=BC,DC=EC,∠ACB=∠DCE=60°,
∴∠ACD+∠DCB=∠ECB+∠DCB=60°,
∴∠ACD=∠BCE,
∴△ACD≌△BCE(SAS);
(2)解:过点C作CH⊥BQ于H,
∵△ABC是等边三角形,AO是角平分线,
∴∠DAC=30°,
∵△ACD≌△BCE,
∴∠PBC=∠DAC=30°,
∴在Rt△BHC中,CH=BC=×8=4,
∵PC=CQ=5,CH=4,
∴PH=QH=3,
∴PQ=6.
一.选择题(共12小题)
1. 的平方根是( )
A. 3 B. ±3 C. D. ±
2.下列运算正确的是( )
A. a2 a3=a6 B. +=2+ C.(x﹣2)(x+3)=x2﹣6 D.(﹣a)2=﹣a2
3.如图,A、B两点在数轴上表示的数分别是a、b,则下列式子中成立的是( )
A.a+b<0 B.﹣a<﹣b C.1﹣2a>1﹣2b D.|a|﹣|b|>0
4.如图,将△ABC绕点A逆时针旋转一定角度,得到△ADE.若∠CAE=65°,∠E=70°,且AD⊥BC,∠BAC的度数为( )
A. 60° B. 75° C. 85° D. 90°
4题 5题 8题
5.在6×6方格中,将图1中的图形N平移后位置如图2所示,则图形N的平移方法中,正确的是)
A. 向下移动1格 B. 向上移动1格 C. 向上移动2格 D. 向下移动2格
6.一直角三角形的两边长分别为3和4.则第三边的长为( )
A. 5 B. C. D. 5或
7.将一等腰直角三角形纸片对折后再对折,得到如图所示的图形,然后将阴影部分剪掉,把剩余部分展开后的平面图形是( )
A. B. C. D.
8.如图,有两颗树,一颗高10米,另一颗高4米,两树相距8米.一只鸟从一颗树的树梢飞到另一颗树的树梢,问小鸟至少飞行( )
A. 8米 B. 10米 C. 12米 D. 14米
9.在面积为15的平行四边形ABCD中,过点A作AE垂直于直线BC于点E,作AF垂直于直线CD于点F,若AB=5,BC=6,则CE+CF的值为( )
A. 11+ B. 11﹣ C. 11+或11﹣ D. 11+或1+
10.下列图形中,既是轴对称图形又是中心对称图形的有( )
A. 4个 B. 3个 C. 2个 D. 1个
10题 11题
11.如图,直角梯形ABCD中,AB∥CD,∠C=90°,∠BDA=90°,AB=a,BD=b,CD=c,BC=d,AD=e,则下列等式成立的是( )
A. b2=ac B. b2=ce C. be=ac D. bd=ae
12.在如图所示的单位正方形网格中,△ABC经过平移后得到△A1B1C1,已知在AC上一点P(2.4,2)平移后的对应点为P1,点P1绕点O逆时针旋转180°,得到对应点P2,则P2点的坐标为( )
A. (1.4,﹣1) B. (1.5,2) C. (1.6,1) D. (2.4,1)
二.填空题(共6小题)
13.如图,AC⊥CD,垂足为点C,BD⊥CD,垂足为点D,AB与CD交于点O.若AC=1,BD=2,CD=4,则AB= _________ .
12题 13题 17题
14.等腰三角形一腰长为5,一边上的高为4,则底边长 _________ .
15.已知实数x,y满足,则以x,y的值为两边长的等腰三角形的周长是 ____ .
16.已知a、b为两个连续整数,且a<<b,则a+b= _________ .
17.如图,把△PQR沿着PQ的方向平移到△P′Q′R′的位置,它们重叠部分的面积是△PQR面积的一半,若PQ=,则此三角形移动的距离PP′= _________ .
18.分析图①,②,④中阴影部分的分布规律,按此规律在图③中画出其中的阴影部分 _________ .
三.解答题(共10小题)
19.计算:|﹣2|+.
20.已知:,求的值.
21.计算:.
22.先化简,再求值.,其中x=1,y=.
23.已知:,求的值.
24.如图,已知点D为等腰直角△ABC内一点,∠CAD=∠CBD=15°,E为AD延长线上的一点,且CE=CA.(1)求证:DE平分∠BDC;(2)若点M在DE上,且DC=DM,求证:ME=BD.
25.已知:△ABC在坐标平面内,三个顶点的坐标分别为A(0,3),B(3,4),C(2,2).(正方形网格中,每个小正方形的边长是1个单位长度)
(1)画出△ABC向下平移4个单位得到的△A1B1C1,并直接写出C1点的坐标;
(2)以点B为位似中心,在网格中画出△A2BC2,使△A2BC2与△ABC位似,且位似比为2:1,并直接写出C2点的坐标及△A2BC2的面积.
26.在△ABC中,AB=AC=5cm,D、E分别是AB,AC的中点,将△EBC沿BC折叠得到△FBC,连接C、D.
(1)求证:四边形DBFC是平行四边形;
(2)若BC=5cm,求D、F两点之间的距离.
27.如图,等边△ABC中,AO是∠BAC的角平分线,D为AO上一点,以CD为一边且在CD下方作等边△CDE,连接BE.
(1)求证:△ACD≌△BCE;
(2)延长BE至Q,P为BQ上一点,连接CP、CQ使CP=CQ=5,若BC=8时,求PQ的长.
2014学年度大庆市房顶中学第二学期初二数学第一次月考
参考答案与试题解析
一.选择题(共12小题)
1.D
2.B
3.C
4.C
5.D
6.D
7.A
8.B
9.D
10.B
11.A
12.C
二.填空题(共6小题)
13. 5 .
14. 6或2或4 .
15. 20 .
16. 9 .
17.
18.见答图
三.解答题(共10小题)
19.计算:|﹣2|+.
解答: 解:原式=2+1×1﹣2+
=.
20.已知:,求的值.
解答: 解:∵a=,
=2﹣,
∴a<1,
∴原式=
=,
=,
=﹣2﹣.
21.计算:.
解答: 解:原式=,
=,
=,
=
22.先化简,再求值.,其中x=1,y=.
解答: 解:原式=,
=,
=﹣,
=0.
当x=1,y=时,原式=0.
23.已知:,求的值.
解答: 解:∵a==2﹣<1,
∴原式==a﹣3+
=2﹣﹣3+2+=1.
24.如图,已知点D为等腰直角△ABC内一点,∠CAD=∠CBD=15°,E为AD延长线上的一点,且CE=CA.
(1)求证:DE平分∠BDC;
(2)若点M在DE上,且DC=DM,求证:ME=BD.
解答: 证明:(1)∵△ABC是等腰直角三角形,
∴∠BAC=∠ABC=45°,
∵∠CAD=∠CBD=15°,
∴∠BAD=∠ABD=45°﹣15°=30°,
∴BD=AD,
∴D在AB的垂直平分线上,
∵AC=BC,
∴C也在AB的垂直平分线上,
即直线CD是AB的垂直平分线,
∴∠ACD=∠BCD=45°,
∴∠CDE=15°+45°=60°,
∴∠BDE=∠DBA+∠BAD=60°;
∴∠CDE=∠BDE,
即DE平分∠BDC.
(2)如图,连接MC.
∵DC=DM,且∠MDC=60°,
∴△MDC是等边三角形,即CM=CD.∠DMC=∠MDC=60°,
∵∠ADC+∠MDC=180°,∠DMC+∠EMC=180°,
∴∠EMC=∠ADC.
又∵CE=CA,
∴∠DAC=∠CEM.
在△ADC与△EMC中,
,
∴△ADC≌△EMC(AAS),
∴ME=AD=BD.
25.已知:△ABC在坐标平面内,三个顶点的坐标分别为A(0,3),B(3,4),C(2,2).(正方形网格中,每个小正方形的边长是1个单位长度)
(1)画出△ABC向下平移4个单位得到的△A1B1C1,并直接写出C1点的坐标;
(2)以点B为位似中心,在网格中画出△A2BC2,使△A2BC2与△ABC位似,且位似比为2:1,并直接写出C2点的坐标及△A2BC2的面积.
解答: 解:(1)如图,△A1B1C1即为所求,C1(2,﹣2);
(2)如图,△A2BC2即为所求,C2(1,0),
△A2BC2的面积:
6×4﹣×2×6﹣×2×4﹣×2×4
=24﹣6﹣4﹣4
=24﹣14
=10.
26.在△ABC中,AB=AC=5cm,D、E分别是AB,AC的中点,将△EBC沿BC折叠得到△FBC,连接C、D.
(1)求证:四边形DBFC是平行四边形;
(2)若BC=5cm,求D、F两点之间的距离.
解答: (1)证明:∵AB=AC=5cm,D、E分别是AB,AC的中点,
∴BD=CE=2.5cm,∠ABC=∠ACB,BC=BC,
∴△BEC≌△CDB,
∴BE=CD,
∵△BFC是△BEC翻折而成,
∴BE=BF,CE=CF,
∴BF=CD,CF=BD,
∴四边形DBFC是平行四边形;
(2)解:连接DF,
∵AB=AC=5cm,BC=5cm,
∴△ABC是等边三角形,
∵D是AB的中点,
∴CD⊥AB,∠BCD=30°,
∴CD=BC cos30°=5×=,
∴四边形DBFC是矩形,
∴BF=CD=
在Rt△BDF中,
DF===5cm.
27.如图,等边△ABC中,AO是∠BAC的角平分线,D为AO上一点,以CD为一边且在CD下方作等边△CDE,连接BE.
(1)求证:△ACD≌△BCE;
(2)延长BE至Q,P为BQ上一点,连接CP、CQ使CP=CQ=5,若BC=8时,求PQ的长.
解答: (1)证明:∵△ABC与△DCE是等边三角形,
∴AC=BC,DC=EC,∠ACB=∠DCE=60°,
∴∠ACD+∠DCB=∠ECB+∠DCB=60°,
∴∠ACD=∠BCE,
∴△ACD≌△BCE(SAS);
(2)解:过点C作CH⊥BQ于H,
∵△ABC是等边三角形,AO是角平分线,
∴∠DAC=30°,
∵△ACD≌△BCE,
∴∠PBC=∠DAC=30°,
∴在Rt△BHC中,CH=BC=×8=4,
∵PC=CQ=5,CH=4,
∴PH=QH=3,
∴PQ=6.
同课章节目录
