北师大版数学八年级下册1.4 角平分线(含解析)
文档属性
| 名称 | 北师大版数学八年级下册1.4 角平分线(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 546.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-23 22:08:59 | ||
图片预览




文档简介
1.4 角平分线
一、选择题(共10题)
三角形中,到三边距离相等的点是
A.三条高线的交点 B.三条中线的交点
C.三条角平分线的交点 D.三边垂直平分线的交点
如图,在 中,, 平分 ,交 于点 ,,垂足为点 ,若 ,则 的长为
A. B. C. D.
如图, 平分 , 于点 ,点 是射线 上的一个动点,若 ,则 的最小值是
A. B. C. D.
如图, 平分 ,,,垂足分别为 ,.下列结论中不一定成立的是
A. B. 平分
C. D. 垂直平分
已知:如图, 是 的角平分线,且 ,则 与 的面积之比为
A. B. C. D.
如图,在 中,,,,按下列步骤作图:
①以点 为圆心,小于 的长为半径作弧,分别交 , 于点 ,;
②分别以点 , 为圆心,大于 的长为半径作弧,两弧交于点 ;
③作射线 交 于点 .
由此可知 的长为
A. B. C. D.
如图, 的三边 ,, 长分别是 ,,.其三条角平分线交于点 ,将 分为三个三角形, 等于
A. B. C. D.
如图,已知 和 都是等腰三角形,,, 交于点 ,连接 .下列结论:① ;② ;③ 平分 ;④ .其中正确的结论有
A. 个 B. 个 C. 个 D. 个
已知:如图,, 是 的中点, 平分 ,,则 为
A. B. C. D.
如图,, 于点 , 于点 ,, 交于点 .给出下列结论:
① ;
② ;
③点 在 的平分线上.
其中,正确的是
A.① B.② C.①② D.①②③
二、填空题(共5题)
角平分线上的点到 距离相等.
关于三角形角平分线的说法:
①两角平分线交点在三角形内;
②两角平分线交点在第三个角的平分线上;
③两角平分线交点到三边距离相等;
④两角平分线交点到三顶点距离相等,
其中正确的是 .
角平分线的判定:角的内部到角的两边的 的点在角的平分线上.用符号语言表示:如图,
于点 , 于点 ,,
.
中,,, 是角平分线,若 ,则 .
如图,在 中,按以下步骤作图:
①以点 为圆心,任意长为半径作弧,分别交 , 于点 ,.
②分别以点 , 为圆心,大于 的长为半径作弧,两弧交于点 .
③作射线 交 于点 .
若 ,, 的面积为 ,则 的面积为 .
三、解答题(共5题)
如图, 是 内的一点,,,垂足分别为 ,,,求证:点 在 的角平分线上.
如图,在 中,已知 , 平分 ,交 于点 ,过点 作 于点 .
(1) 求证:;
(2) 若 ,,求 的长.
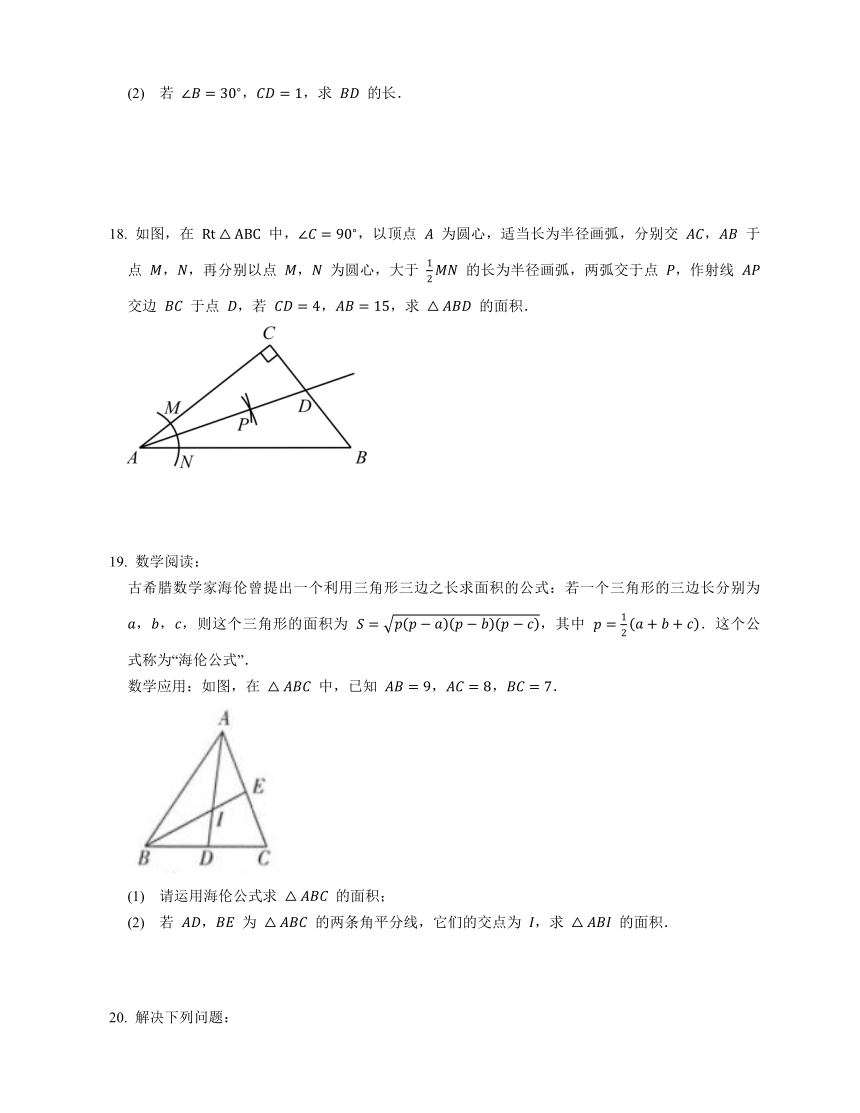
如图,在 中,,以顶点 为圆心,适当长为半径画弧,分别交 , 于点 ,,再分别以点 , 为圆心,大于 的长为半径画弧,两弧交于点 ,作射线 交边 于点 ,若 ,,求 的面积.
数学阅读:
古希腊数学家海伦曾提出一个利用三角形三边之长求面积的公式:若一个三角形的三边长分别为 ,,,则这个三角形的面积为 ,其中 .这个公式称为“海伦公式”.
数学应用:如图,在 中,已知 ,,.
(1) 请运用海伦公式求 的面积;
(2) 若 , 为 的两条角平分线,它们的交点为 ,求 的面积.
解决下列问题:
(1) 阅读理解:
我们知道,只用直尺和圆规不能解决的三个经典希腊问题之一是三等分任意角,但是这个任务可以借助如图所示的一边上有刻度的勾尺完成,勾尺的直角顶点为 ,“宽臂”的宽度 (这个条件很重要哦!),勾尺的一边 满足 ,, 三点共线(所以 ).
下面以三等分 为例说明利用勾尺三等分锐角的过程:
第一步:画直线 使 ,且这两条平行线的距离等于 ;
第二步:移动勾尺到合适位置,使其顶点 落在 上,使勾尺的 边经过点 ,同时让点 落在 的 边上;
第三步:标记此时点 和点 所在位置,作射线 和射线 .
请完成第三步操作,则图中 的三等分线是射线 , ;
(2) 请你完成证明 的过程;
(3) 在()的条件下探究: 是否成立?如果成立,请说明理由;如果不成立,请在下图中 的外部画出 (无需写画法,保留画图痕迹即可).
答案
一、选择题(共10题)
1. 【答案】C
【解析】三角形中,到三边距离相等的点是三条角平分线的交点.
2. 【答案】B
【解析】 平分 交 于点 ,,,
.【角平分线的性质:角平分线上的点到角的两边的距离相等】
故选:B.
3. 【答案】B
4. 【答案】D
【解析】 平分 ,,,
,故A选项正确;
在 和 中,
(),
,,故B,C选项正确;
由等腰三角形三线合一的性质, 垂直平分 , 不一定垂直平分 ,故D选项错误.
5. 【答案】B
【解析】过点 作 于 , 于 ,
为 的平分线,
,
又 ,
.
6. 【答案】B
7. 【答案】C
【解析】如图,过点 作 ,,,垂足分别为 ,,.
三条角平分线交于点 ,
,
8. 【答案】C
【解析】思路分析:“手拉手全等”模型的应用.
如图,作 于点 , 于点 ,设 交 于点 .
,
,
,,
,
,,故①正确.
,
,
,故②正确.
,,,
,
平分 ,
,故④正确.
若③成立,则 ,
,
,推出 ,由题意知, 不一定等于 ,
不一定平分 ,故③错误.
故选:C.
9. 【答案】A
【解析】思路分析:“角平分线”模型问题,注意角平分线的性质与判定.
过点 作 于点 .
平分 ,且 是 的中点,
,
又 ,,
平分 .
,
.
故选:A.
10. 【答案】D
二、填空题(共5题)
11. 【答案】角两边的
12. 【答案】①②③
【解析】结论①②可以实际操作验证,结论③④可根据角平分线的性质判断.
13. 【答案】距离相等; 平分
14. 【答案】
15. 【答案】
【解析】由作图可知, 为 的平分线,过 作 于 , 于 .
易得 ,
,
,
,
,
.
三、解答题(共5题)
16. 【答案】如图,连接 并延长.
,,
.
在 和 中,
,
.
,,
点 在 的角平分线上.
17. 【答案】
(1) 平分 ,,,
,.
在 和 中,
,,
.
(2) ,,
.
,
.
18. 【答案】由题意可知 为 的平分线,过点 作 于点 .
,,
,
,
.
19. 【答案】
(1) ,,,
,
.
(2) 过点 作 ,,,垂足为 ,,,连接 ,
, 为 的两条角平分线,
,
,
,
解得 ,
故 .
20. 【答案】
(1) 作射线 , 如解图.
;
(2) ,,
.
.
,,,
.
.
(3) 在()的条件下探究: 不成立,在 外部所画 如解图.
一、选择题(共10题)
三角形中,到三边距离相等的点是
A.三条高线的交点 B.三条中线的交点
C.三条角平分线的交点 D.三边垂直平分线的交点
如图,在 中,, 平分 ,交 于点 ,,垂足为点 ,若 ,则 的长为
A. B. C. D.
如图, 平分 , 于点 ,点 是射线 上的一个动点,若 ,则 的最小值是
A. B. C. D.
如图, 平分 ,,,垂足分别为 ,.下列结论中不一定成立的是
A. B. 平分
C. D. 垂直平分
已知:如图, 是 的角平分线,且 ,则 与 的面积之比为
A. B. C. D.
如图,在 中,,,,按下列步骤作图:
①以点 为圆心,小于 的长为半径作弧,分别交 , 于点 ,;
②分别以点 , 为圆心,大于 的长为半径作弧,两弧交于点 ;
③作射线 交 于点 .
由此可知 的长为
A. B. C. D.
如图, 的三边 ,, 长分别是 ,,.其三条角平分线交于点 ,将 分为三个三角形, 等于
A. B. C. D.
如图,已知 和 都是等腰三角形,,, 交于点 ,连接 .下列结论:① ;② ;③ 平分 ;④ .其中正确的结论有
A. 个 B. 个 C. 个 D. 个
已知:如图,, 是 的中点, 平分 ,,则 为
A. B. C. D.
如图,, 于点 , 于点 ,, 交于点 .给出下列结论:
① ;
② ;
③点 在 的平分线上.
其中,正确的是
A.① B.② C.①② D.①②③
二、填空题(共5题)
角平分线上的点到 距离相等.
关于三角形角平分线的说法:
①两角平分线交点在三角形内;
②两角平分线交点在第三个角的平分线上;
③两角平分线交点到三边距离相等;
④两角平分线交点到三顶点距离相等,
其中正确的是 .
角平分线的判定:角的内部到角的两边的 的点在角的平分线上.用符号语言表示:如图,
于点 , 于点 ,,
.
中,,, 是角平分线,若 ,则 .
如图,在 中,按以下步骤作图:
①以点 为圆心,任意长为半径作弧,分别交 , 于点 ,.
②分别以点 , 为圆心,大于 的长为半径作弧,两弧交于点 .
③作射线 交 于点 .
若 ,, 的面积为 ,则 的面积为 .
三、解答题(共5题)
如图, 是 内的一点,,,垂足分别为 ,,,求证:点 在 的角平分线上.
如图,在 中,已知 , 平分 ,交 于点 ,过点 作 于点 .
(1) 求证:;
(2) 若 ,,求 的长.
如图,在 中,,以顶点 为圆心,适当长为半径画弧,分别交 , 于点 ,,再分别以点 , 为圆心,大于 的长为半径画弧,两弧交于点 ,作射线 交边 于点 ,若 ,,求 的面积.
数学阅读:
古希腊数学家海伦曾提出一个利用三角形三边之长求面积的公式:若一个三角形的三边长分别为 ,,,则这个三角形的面积为 ,其中 .这个公式称为“海伦公式”.
数学应用:如图,在 中,已知 ,,.
(1) 请运用海伦公式求 的面积;
(2) 若 , 为 的两条角平分线,它们的交点为 ,求 的面积.
解决下列问题:
(1) 阅读理解:
我们知道,只用直尺和圆规不能解决的三个经典希腊问题之一是三等分任意角,但是这个任务可以借助如图所示的一边上有刻度的勾尺完成,勾尺的直角顶点为 ,“宽臂”的宽度 (这个条件很重要哦!),勾尺的一边 满足 ,, 三点共线(所以 ).
下面以三等分 为例说明利用勾尺三等分锐角的过程:
第一步:画直线 使 ,且这两条平行线的距离等于 ;
第二步:移动勾尺到合适位置,使其顶点 落在 上,使勾尺的 边经过点 ,同时让点 落在 的 边上;
第三步:标记此时点 和点 所在位置,作射线 和射线 .
请完成第三步操作,则图中 的三等分线是射线 , ;
(2) 请你完成证明 的过程;
(3) 在()的条件下探究: 是否成立?如果成立,请说明理由;如果不成立,请在下图中 的外部画出 (无需写画法,保留画图痕迹即可).
答案
一、选择题(共10题)
1. 【答案】C
【解析】三角形中,到三边距离相等的点是三条角平分线的交点.
2. 【答案】B
【解析】 平分 交 于点 ,,,
.【角平分线的性质:角平分线上的点到角的两边的距离相等】
故选:B.
3. 【答案】B
4. 【答案】D
【解析】 平分 ,,,
,故A选项正确;
在 和 中,
(),
,,故B,C选项正确;
由等腰三角形三线合一的性质, 垂直平分 , 不一定垂直平分 ,故D选项错误.
5. 【答案】B
【解析】过点 作 于 , 于 ,
为 的平分线,
,
又 ,
.
6. 【答案】B
7. 【答案】C
【解析】如图,过点 作 ,,,垂足分别为 ,,.
三条角平分线交于点 ,
,
8. 【答案】C
【解析】思路分析:“手拉手全等”模型的应用.
如图,作 于点 , 于点 ,设 交 于点 .
,
,
,,
,
,,故①正确.
,
,
,故②正确.
,,,
,
平分 ,
,故④正确.
若③成立,则 ,
,
,推出 ,由题意知, 不一定等于 ,
不一定平分 ,故③错误.
故选:C.
9. 【答案】A
【解析】思路分析:“角平分线”模型问题,注意角平分线的性质与判定.
过点 作 于点 .
平分 ,且 是 的中点,
,
又 ,,
平分 .
,
.
故选:A.
10. 【答案】D
二、填空题(共5题)
11. 【答案】角两边的
12. 【答案】①②③
【解析】结论①②可以实际操作验证,结论③④可根据角平分线的性质判断.
13. 【答案】距离相等; 平分
14. 【答案】
15. 【答案】
【解析】由作图可知, 为 的平分线,过 作 于 , 于 .
易得 ,
,
,
,
,
.
三、解答题(共5题)
16. 【答案】如图,连接 并延长.
,,
.
在 和 中,
,
.
,,
点 在 的角平分线上.
17. 【答案】
(1) 平分 ,,,
,.
在 和 中,
,,
.
(2) ,,
.
,
.
18. 【答案】由题意可知 为 的平分线,过点 作 于点 .
,,
,
,
.
19. 【答案】
(1) ,,,
,
.
(2) 过点 作 ,,,垂足为 ,,,连接 ,
, 为 的两条角平分线,
,
,
,
解得 ,
故 .
20. 【答案】
(1) 作射线 , 如解图.
;
(2) ,,
.
.
,,,
.
.
(3) 在()的条件下探究: 不成立,在 外部所画 如解图.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
