《数学广角抽屉原理鸽巢原理》(课件)人教版六年级下册数学(共20张PPT)
文档属性
| 名称 | 《数学广角抽屉原理鸽巢原理》(课件)人教版六年级下册数学(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-23 15:13:26 | ||
图片预览



文档简介
(共20张PPT)
鸽巢问题
(抽屉原理)
抢凳子游戏
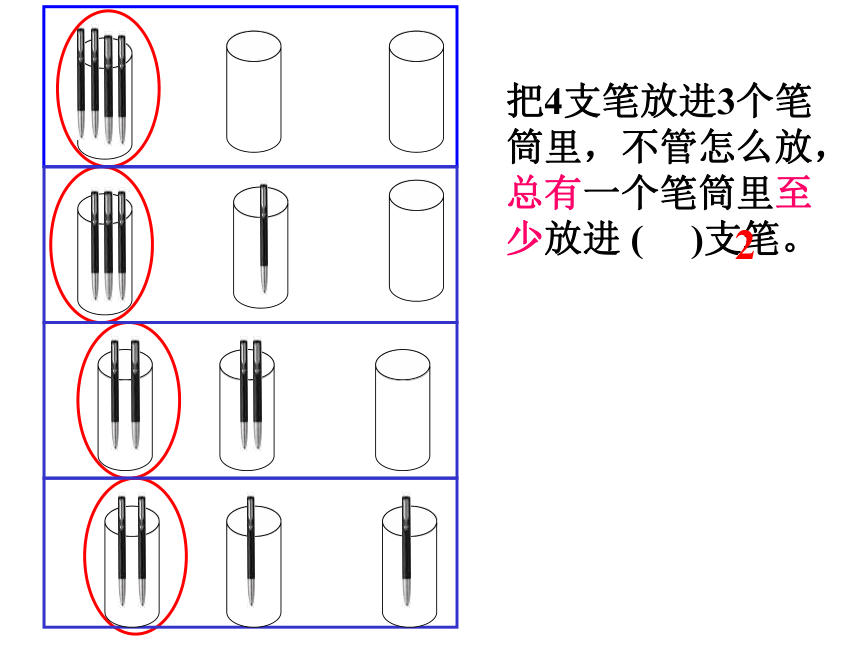
把4支笔放进3个笔筒里,不管怎么放,
总有一个笔筒里至少放进2支笔。
这句话对吗?为什么?
把4支笔放进3个笔筒里,不管怎么放,
总有一个笔筒里至少放进2支笔。
这句话对吗?为什么?
把4支笔放进3个笔筒里,不管怎么放,
总有一个笔筒里至少放进2支笔。
这句话对吗?为什么?
把4支笔放进3个笔筒里,不管怎么放,
总有一个笔筒里至少放进2支笔。
这句话对吗?为什么?
把4支笔放进3个笔筒里,不管怎么放,
总有一个笔筒里至少放进2支笔。
这句话对吗?为什么?
把4支笔放进3个笔筒里,不管怎么放,总有一个笔筒里至少放进 ( )支笔。
2
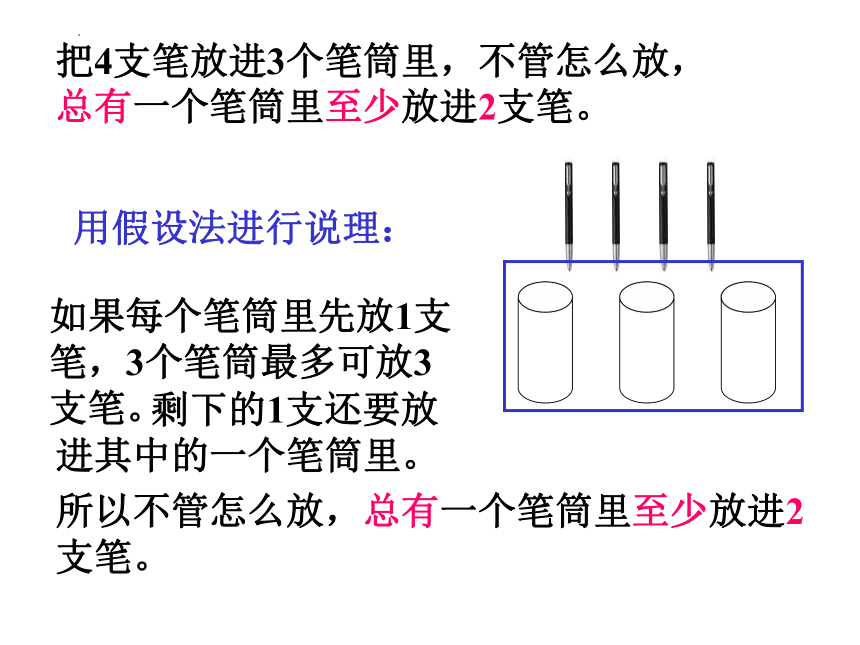
用假设法进行说理:
如果每个笔筒里先放1支笔,3个笔筒最多可放3支笔。
把4支笔放进3个笔筒里,不管怎么放,
总有一个笔筒里至少放进2支笔。
剩下的1支还要放进其中的一个笔筒里。
所以不管怎么放,总有一个笔筒里至少放进2支笔。
答:
如果每个笔筒里先放1支笔,
把5支笔放进4个笔筒里,不管怎么放,总有一个笔筒里至少放进2支笔。这句话对吗?为什么?
剩下的1支还要放进其中的一个笔筒里。
最多可放4支。
所以不管怎么放,总有一个笔筒里至少放进2支笔。
把6支笔放进5个笔筒里,不管怎么放,总有一个笔筒里至少放进2支笔,这句话对吗?为什么?
答:
如果…,
剩下的…。
所以…。
只要放的铅笔数比笔筒的数量多( ),总有一个笔筒里至少放进2枝笔。
把4枝笔放进3个笔筒里,不管怎么放,总有一个笔筒里至少放进2枝笔。
把5枝笔放进4个笔筒里,不管怎么放,总有一个笔筒里至少放进2枝笔。
把( ) 枝笔放进( )个笔筒里,不管怎么放,总有一个笔筒里至少放进2枝笔。
我发现:
待分物体
抽屉
把6枝笔放进5个笔筒里,不管怎么放,总有一个笔筒里至少放进2枝笔。
“抽屉原理” 最早是由德国数学家狄里克雷(Dirichlet)提出并运用于解决数学问题的,所以又称“狄里克雷原理”。
知识链接
(二)6只鸽子飞进5个鸽巢,
总有一个鸽巢至少飞进2只鸽子。
2
狄里克雷原理有两个经典案例:
(一)把10个苹果放进9个抽屉里,
总有一个抽屉里至少放进 个苹果。
5只鸽子飞回3个鸽笼,总有一个鸽笼至少飞进2只鸽子。为什么?
只要待分物体的数量比抽屉的数量多
8只鸽子飞回5个鸽舍,总有一个鸽笼至少飞进2只鸽子。为什么?
你还能想到生活中“鸽巢问题”吗?
三个小朋友同行,其中必有
两个小朋友性别相同。
三个
性别
小朋友
应用练习
3个物体
在我们班的任意13名同学中,至少有2名同学的生日在同一个月。
根据抽屉原理,总有一个抽屉里至少放进2个物体,
13个物体放进12个抽屉,
也就是说,至少有2名同学的生日在同一个月。
1年有12个月
13个生日
12个
13个物体
四种花色
抽 牌
一幅扑克,拿走大、小王后还有52张牌,任意抽出其中的 5张牌,同种花色的至少有几张?为什么
你敢肯定 。
至少有两个面的颜色相同
5种颜色
每面都喷
鸽巢问题
(抽屉原理)
抢凳子游戏
把4支笔放进3个笔筒里,不管怎么放,
总有一个笔筒里至少放进2支笔。
这句话对吗?为什么?
把4支笔放进3个笔筒里,不管怎么放,
总有一个笔筒里至少放进2支笔。
这句话对吗?为什么?
把4支笔放进3个笔筒里,不管怎么放,
总有一个笔筒里至少放进2支笔。
这句话对吗?为什么?
把4支笔放进3个笔筒里,不管怎么放,
总有一个笔筒里至少放进2支笔。
这句话对吗?为什么?
把4支笔放进3个笔筒里,不管怎么放,
总有一个笔筒里至少放进2支笔。
这句话对吗?为什么?
把4支笔放进3个笔筒里,不管怎么放,总有一个笔筒里至少放进 ( )支笔。
2
用假设法进行说理:
如果每个笔筒里先放1支笔,3个笔筒最多可放3支笔。
把4支笔放进3个笔筒里,不管怎么放,
总有一个笔筒里至少放进2支笔。
剩下的1支还要放进其中的一个笔筒里。
所以不管怎么放,总有一个笔筒里至少放进2支笔。
答:
如果每个笔筒里先放1支笔,
把5支笔放进4个笔筒里,不管怎么放,总有一个笔筒里至少放进2支笔。这句话对吗?为什么?
剩下的1支还要放进其中的一个笔筒里。
最多可放4支。
所以不管怎么放,总有一个笔筒里至少放进2支笔。
把6支笔放进5个笔筒里,不管怎么放,总有一个笔筒里至少放进2支笔,这句话对吗?为什么?
答:
如果…,
剩下的…。
所以…。
只要放的铅笔数比笔筒的数量多( ),总有一个笔筒里至少放进2枝笔。
把4枝笔放进3个笔筒里,不管怎么放,总有一个笔筒里至少放进2枝笔。
把5枝笔放进4个笔筒里,不管怎么放,总有一个笔筒里至少放进2枝笔。
把( ) 枝笔放进( )个笔筒里,不管怎么放,总有一个笔筒里至少放进2枝笔。
我发现:
待分物体
抽屉
把6枝笔放进5个笔筒里,不管怎么放,总有一个笔筒里至少放进2枝笔。
“抽屉原理” 最早是由德国数学家狄里克雷(Dirichlet)提出并运用于解决数学问题的,所以又称“狄里克雷原理”。
知识链接
(二)6只鸽子飞进5个鸽巢,
总有一个鸽巢至少飞进2只鸽子。
2
狄里克雷原理有两个经典案例:
(一)把10个苹果放进9个抽屉里,
总有一个抽屉里至少放进 个苹果。
5只鸽子飞回3个鸽笼,总有一个鸽笼至少飞进2只鸽子。为什么?
只要待分物体的数量比抽屉的数量多
8只鸽子飞回5个鸽舍,总有一个鸽笼至少飞进2只鸽子。为什么?
你还能想到生活中“鸽巢问题”吗?
三个小朋友同行,其中必有
两个小朋友性别相同。
三个
性别
小朋友
应用练习
3个物体
在我们班的任意13名同学中,至少有2名同学的生日在同一个月。
根据抽屉原理,总有一个抽屉里至少放进2个物体,
13个物体放进12个抽屉,
也就是说,至少有2名同学的生日在同一个月。
1年有12个月
13个生日
12个
13个物体
四种花色
抽 牌
一幅扑克,拿走大、小王后还有52张牌,任意抽出其中的 5张牌,同种花色的至少有几张?为什么
你敢肯定 。
至少有两个面的颜色相同
5种颜色
每面都喷
