【新课标】3.3三视图(2) 课件(共30张PPT)
文档属性
| 名称 | 【新课标】3.3三视图(2) 课件(共30张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-23 17:39:29 | ||
图片预览








文档简介
(共30张PPT)
3.3三视图(2)
湘教版 九年级下册
教学内容分析
本节在上节学习的基础上,继续研究简单立体图形的三视图的画法,学生综合考虑三视图,想象出立体图形,培养了几何直观能力,提高了学生的空间想象力。
教学目标
1.掌握简单立体图形的三视图的画法(重点)
2.能综合考虑三视图,想象出立体图形(难点)
3.培养学生的空间想象能力。
核心素养分析
本节研究简单立体图形的三视图的画法,学生综合考虑三视图,想象出立体图形,发展了学生的空间想象能力。
新知导入
什么是三视图?画三视图遵循的原则?
从前后、左右、上下三个方向观察物体,能够比较全面地了解物体的大小和形状,我们把主视图、左视图、俯视图统称为三视图。
长对正,高平齐,宽相等
新知讲解
你能根据简单物体的三视图描述几何体吗?
新知讲解
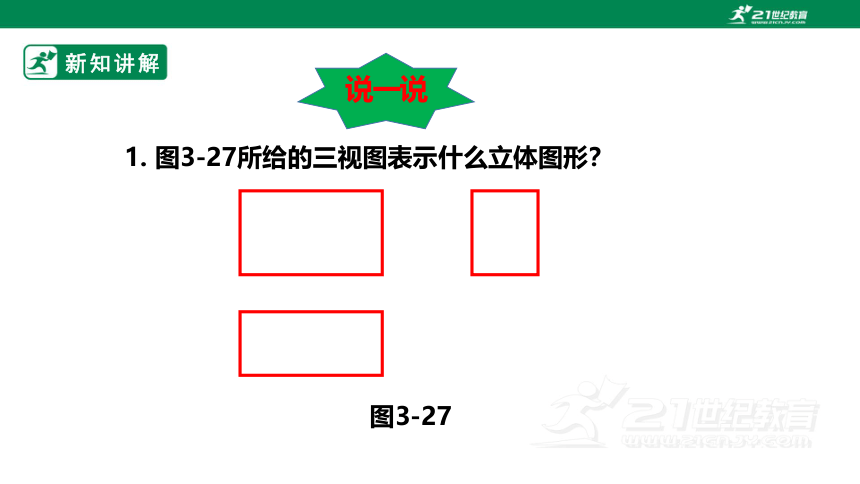
1. 图3-27所给的三视图表示什么立体图形?
说一说
图3-27
新知讲解
从三个方向看立体图形,图像都是矩形,因此这个物体是长方体.
新知讲解
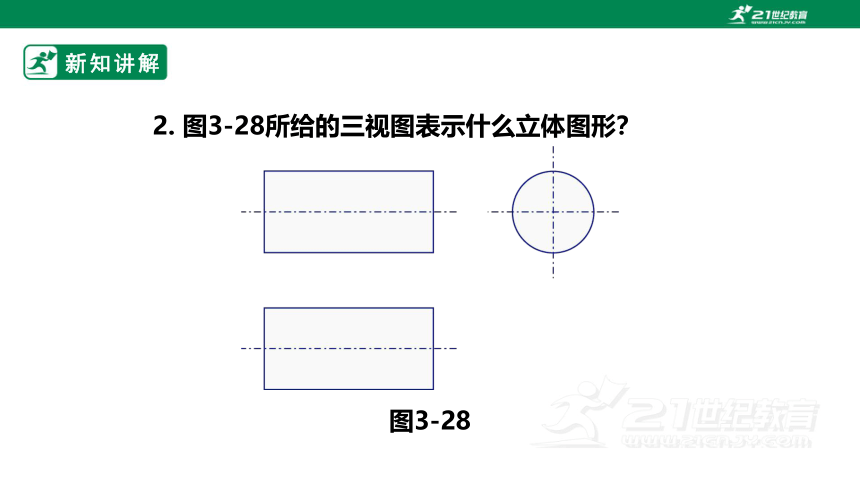
2. 图3-28所给的三视图表示什么立体图形?
图3-28
新知讲解
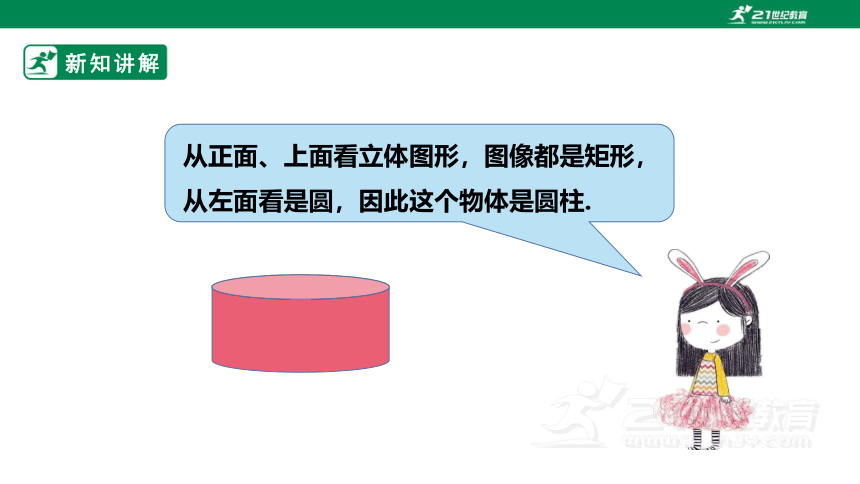
从正面、上面看立体图形,图像都是矩形,从左面看是圆,因此这个物体是圆柱.
新知讲解
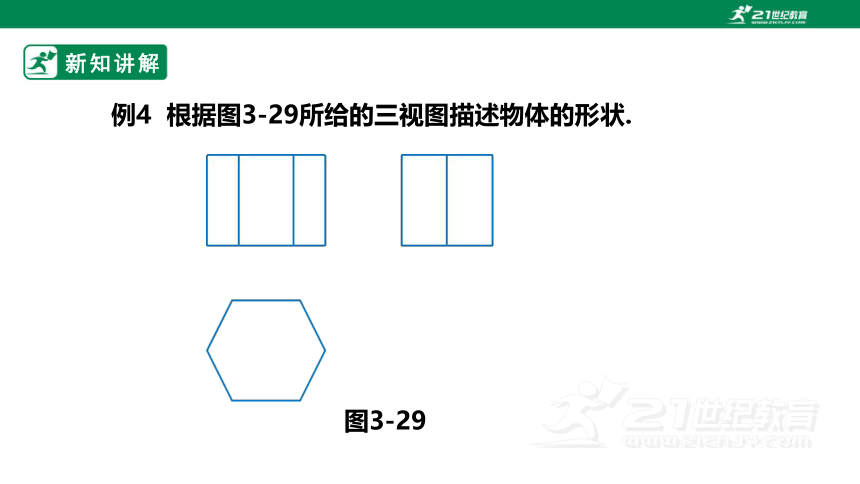
图3-29
例4 根据图3-29所给的三视图描述物体的形状.
新知讲解
分析:由主视图可知,物体的正面是矩形的样子,且中间有两条棱(实线)可见到;
由俯视图可知,由上向下看物体是正六边形的样子;
由左视图可知,物体的侧面是矩形的样子,且中间有一条棱可见到.
综合各视图可知,该物体是正六棱柱.
新知讲解
图3-30
解:物体是正六棱柱,如图3-30所示.
新知讲解
例5 如图3-31是一个零件的三视图,试描述出这个零件的形状.
图3-31
新知讲解
解:这个零件由两部分组成:
上面是一个圆柱,下面是一个长方体, 圆柱立于长方体的中央(如图3-32).
新知讲解
总结
想象和综合
三视图
物体的形状
由三视图想象立体图形,要先根据主视图、俯视图和左视图想象立体图形的前面、上面和左侧面,然后再综合起来考虑整体图形.
变式 一个几何体是由一些大小相同的小正方块摆成的,其从上面看与从前面看所得到的图形如图所示,则组成这个几何体的小正方块最多有 ( )
A. 4个 B. 5个 C. 6个 D. 7个
C
新知讲解
解:综合从上面看得到的图形和从正面看得到的图形,
这个几何体最下面一层有3个正方体,最上面一层最多有
3个正方体,
所以组成这个几何体的小正方块最多有6个.
故选C.
新知讲解
1、先在俯视图的各个小正方形中填上该处小立方体叠加的个数,然后相加即得总数;
2、由这些个数想象出几何体的形状。
新知讲解
题中给出三视图,怎样求组成几何体的小立方体的个数?
1.一个几何体的三视图如图所示,该几何体是( )
课堂练习
A
A. B.
C. D.
解:由于俯视图为圆形可得为球、圆柱、圆锥.
主视图和左视图为三角形可得此几何体为圆锥.
故选A.
课堂练习
课堂练习
2.如图,一个几何体的主视图和左视图都是边长为6的等边三角形,俯视图是直径为6的圆,则此几何体的全面积是( )
A. 18π B. 24π C. 27π D. 42π
C
课堂练习
解:由三视图可知,这个几何体是圆锥,
圆锥的全面积=π×32+π×3×6=27πcm2
故选:C.
课堂练习
3.一个几何体的三视图如图所示,则该几何体的表面积为______
3π+4
课堂练习
解:观察该几何体的三视图发现其为半个圆柱,
半圆柱的直径为2,高为1,
故其表面积为:π×12+(π+2)×2=3π+4,
故答案为:3π+4.
总结
想象和综合
三视图
物体的形状
由三视图想象立体图形,要先根据主视图、俯视图和左视图想象立体图形的前面、上面和左侧面,然后再综合起来考虑整体图形.
课堂总结
板书设计
3.3三视图(2)
1. 画三视图
2.由三视图想象原来的立体图形
作业布置
必做题:课本习题3.3的第4题
选做题:练习册本课时的习题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
3.3三视图(2)
湘教版 九年级下册
教学内容分析
本节在上节学习的基础上,继续研究简单立体图形的三视图的画法,学生综合考虑三视图,想象出立体图形,培养了几何直观能力,提高了学生的空间想象力。
教学目标
1.掌握简单立体图形的三视图的画法(重点)
2.能综合考虑三视图,想象出立体图形(难点)
3.培养学生的空间想象能力。
核心素养分析
本节研究简单立体图形的三视图的画法,学生综合考虑三视图,想象出立体图形,发展了学生的空间想象能力。
新知导入
什么是三视图?画三视图遵循的原则?
从前后、左右、上下三个方向观察物体,能够比较全面地了解物体的大小和形状,我们把主视图、左视图、俯视图统称为三视图。
长对正,高平齐,宽相等
新知讲解
你能根据简单物体的三视图描述几何体吗?
新知讲解
1. 图3-27所给的三视图表示什么立体图形?
说一说
图3-27
新知讲解
从三个方向看立体图形,图像都是矩形,因此这个物体是长方体.
新知讲解
2. 图3-28所给的三视图表示什么立体图形?
图3-28
新知讲解
从正面、上面看立体图形,图像都是矩形,从左面看是圆,因此这个物体是圆柱.
新知讲解
图3-29
例4 根据图3-29所给的三视图描述物体的形状.
新知讲解
分析:由主视图可知,物体的正面是矩形的样子,且中间有两条棱(实线)可见到;
由俯视图可知,由上向下看物体是正六边形的样子;
由左视图可知,物体的侧面是矩形的样子,且中间有一条棱可见到.
综合各视图可知,该物体是正六棱柱.
新知讲解
图3-30
解:物体是正六棱柱,如图3-30所示.
新知讲解
例5 如图3-31是一个零件的三视图,试描述出这个零件的形状.
图3-31
新知讲解
解:这个零件由两部分组成:
上面是一个圆柱,下面是一个长方体, 圆柱立于长方体的中央(如图3-32).
新知讲解
总结
想象和综合
三视图
物体的形状
由三视图想象立体图形,要先根据主视图、俯视图和左视图想象立体图形的前面、上面和左侧面,然后再综合起来考虑整体图形.
变式 一个几何体是由一些大小相同的小正方块摆成的,其从上面看与从前面看所得到的图形如图所示,则组成这个几何体的小正方块最多有 ( )
A. 4个 B. 5个 C. 6个 D. 7个
C
新知讲解
解:综合从上面看得到的图形和从正面看得到的图形,
这个几何体最下面一层有3个正方体,最上面一层最多有
3个正方体,
所以组成这个几何体的小正方块最多有6个.
故选C.
新知讲解
1、先在俯视图的各个小正方形中填上该处小立方体叠加的个数,然后相加即得总数;
2、由这些个数想象出几何体的形状。
新知讲解
题中给出三视图,怎样求组成几何体的小立方体的个数?
1.一个几何体的三视图如图所示,该几何体是( )
课堂练习
A
A. B.
C. D.
解:由于俯视图为圆形可得为球、圆柱、圆锥.
主视图和左视图为三角形可得此几何体为圆锥.
故选A.
课堂练习
课堂练习
2.如图,一个几何体的主视图和左视图都是边长为6的等边三角形,俯视图是直径为6的圆,则此几何体的全面积是( )
A. 18π B. 24π C. 27π D. 42π
C
课堂练习
解:由三视图可知,这个几何体是圆锥,
圆锥的全面积=π×32+π×3×6=27πcm2
故选:C.
课堂练习
3.一个几何体的三视图如图所示,则该几何体的表面积为______
3π+4
课堂练习
解:观察该几何体的三视图发现其为半个圆柱,
半圆柱的直径为2,高为1,
故其表面积为:π×12+(π+2)×2=3π+4,
故答案为:3π+4.
总结
想象和综合
三视图
物体的形状
由三视图想象立体图形,要先根据主视图、俯视图和左视图想象立体图形的前面、上面和左侧面,然后再综合起来考虑整体图形.
课堂总结
板书设计
3.3三视图(2)
1. 画三视图
2.由三视图想象原来的立体图形
作业布置
必做题:课本习题3.3的第4题
选做题:练习册本课时的习题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
