2023年河南省普通高中学业水平考试数学仿真模拟卷(七)(2月)(Word版含解析)
文档属性
| 名称 | 2023年河南省普通高中学业水平考试数学仿真模拟卷(七)(2月)(Word版含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 143.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-23 09:48:05 | ||
图片预览



文档简介
河南省普通高中学业水平考试(2019版新教材)
数学仿真模拟卷(七)
一、选择题(本大题共16小题,每题3分,共48分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.若集合A={x|-2<x<1},B={x |x<-1或x>3},则A∩B=( )
A.{x|-2<x<-1} B.{x|-2<x<3} C.{x|-1<x<1} D.{x|1<x<3}
2.已知命题p:x为自然数,命题q:x为整数,则p是q的( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
3.某学校有高中学生1 000人,其中高一年级、高二年级、高三年级的人数分别为320,300,380.为调查学生参加“社区志愿服务”的意向,现采用分层随机抽样的方法从中抽取一个容量为100的样本,那么应抽取高二年级学生的人数为( )
A.68 B.38 C.32 D.30
4.已知复数a+bi= (i是虚数单位,a,b∈R),则a+b等于( )
A.-2 B.-1 C.0 D.2
5.某校高一年级15个班参加朗诵比赛的得分如下:
91 89 90 92 94 87 93 96 91 85 89 93 88 98 93
则这组数据的60%分位数、90%分位数分别为( )
A.92,96 B.93,96 C.92.5,95 D.92.5,96
6.在△ABC中,若A=60°,C=45°,c=,则a等于( )
A.1 B. C. D.2
7.已知底面边长为1,侧棱长为的正四棱柱的各顶点均在同一球面上,则该球的体积为( )
A. B.4π C.2π D.
8.若集合A={x|ax2-ax+1<0}= ,则实数a的取值范围是( )
A.(0,4) B.[0,4) C.(0,4] D.[0,4]
9.已知x>0,y>0,且x+2y=2,则xy( )
A.有最大值为1 B.有最小值为1 C.有最大值为 D.有最小值为
10.已知向量a,b满足|a|=1,|b|=2,|a-b|=2,则|a+b|等于( )
A.1 B. C. D.
11.函数f(x)=x-的零点个数是( )
A.0 B.1 C.2 D.3
12.甲、乙两个人进行“剪子、包袱、锤”的游戏,两人都随机出拳,则一次游戏两人平局的概率为( )
A. B. C. D.
13.“十一”期间,高速公路车辆较多.某调查公司在一服务区从七座以下小型汽车中抽取了40名驾驶员进行询问调查,将他们在某段高速公路的车速(km/h)分成六段:[60,65),[65,70),[70,75),[75,80),[80,85),[85,90],得到如图所示的频率分布直方图.下列结论错误的是( )
A.这40辆小型汽车车速的众数的估计值为77.5
B.在该服务区任意抽取一辆车,车速超过80 km/h的概率为0.35
C.若从车速在[60,70)的车辆中任意抽取2辆,则至少有一辆车的车速在[65,70)的概率为
D.若从车速在[60,70)的车辆中任意抽取2辆,则车速都在[60,65)内的概率为
14.设D,E为正三角形ABC中BC边上的两个三等分点,且BC=2,则·等于( )
A. B. C. D.
15.在△ABC中,内角A,B,C的对边分别为a,b,c.若△ABC的面积为S,且a=1,4S=b2+c2-1,则△ABC外接圆的面积为( )
A.4π B.2π C.π D.
16.已知函数①y=sin x+cos x,②y=2sin xcos x,则下列结论正确的是( )
A.两个函数的图象均关于点成中心对称图形
B.两个函数的图象均关于直线x=-成轴对称图形
C.两个函数在区间上都是单调递增函数
D.两个函数的最小正周期相同
二、填空题(本大题共7小题,每小题3分,共21分)
17.已知非零向量a,b满足|a|=4|b|,且b⊥(a+2b),则a与b的夹角为________.
18.某人5次上班途中所花的时间(单位:分钟)分别为x,y,10,11,9.已知这组数据的平均数为10,方差为2,则|x-y|的值为________.
19.某种病毒经30分钟繁殖为原来的2倍,且知病毒的繁殖规律为y=ekt(其中k为常数,t表示时间,单位:小时,y表示病毒个数),则经过5小时,1个病毒能繁殖为________个.
20.已知sin(π-α)=,cos(α-β)=,0<β<α<,角β的大小为________.
21.在△ABC中,角A,B,C的对边分别是a,b,c,已知a=b,c2=2b2(1-sin C),则C=________.
22.如图所示,在空间四边形ABCD中,E,H分别是AB,AD的中点,F,G分别是CB,CD上的点,且==,若BD=6,四边形EFGH的面积为28,则直线EH,FG之间的距离为________.
23.甲、乙、丙三人向同一飞机射击,设击中的概率分别为0.4,0.5,0.8,若只有1人击中,则飞机被击落的概率为0.2,若2人击中,则飞机被击落的概率为0.6,若3人击中,则飞机一定被击落,则飞机被击落的概率为________.
三、解答题(本大题共6小题,共31分,解答应写出文字说明、证明过程或演算步骤)
24.设α,β是锐角,sin α=,cos(α+β)=-,求β的值.
25.已知|a|=4,|b|=8,a与b的夹角是120°.
(1)求a·b的值及|a+b|的值;
(2)当k为何值时,(a+2b)⊥(ka-b)
26.某集团公司为了加强企业管理,树立企业形象,考虑在公司内部对迟到现象进行处罚,现在员工中随机抽取200人进行调查,当不处罚时,有80人迟到,处罚时,得到如下数据:
处罚金额x(单位:元) 50 100 150 200
迟到的人数y 50 40 20 0
若用表中数据所得频率代替概率.
(1)当处罚金额定为100元时,员工迟到的概率会比不进行处罚时降低多少?
(2)将选取的200人中会迟到的员工分为A,B两类:A类员工在罚金不超过100元时就会改正行为;B类是其他员工.现对A类与B类员工按分层随机抽样的方法抽取4人依次进行深度问卷调查,则前两位均为B类员工的概率是多少?
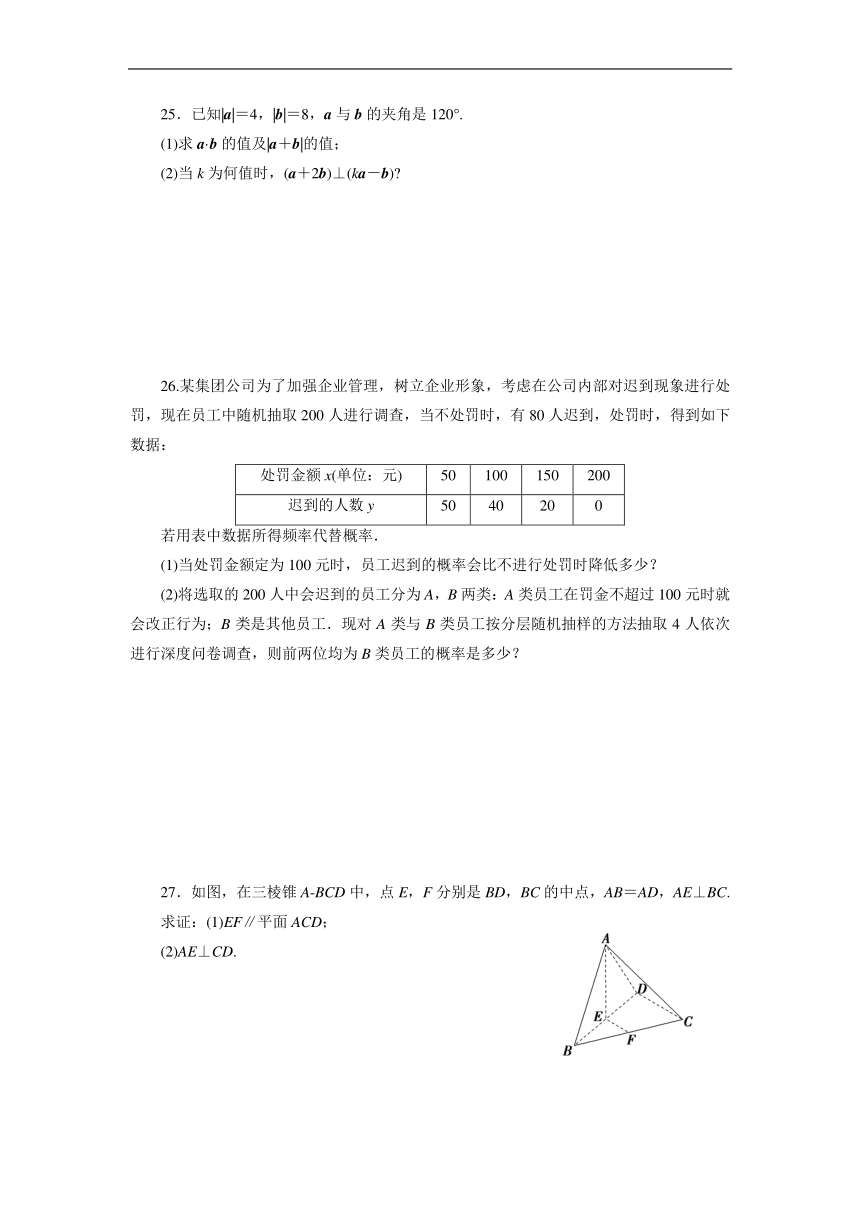
27.如图,在三棱锥A BCD中,点E,F分别是BD,BC的中点,AB=AD,AE⊥BC.
求证:(1)EF∥平面ACD;
(2)AE⊥CD.
28.已知函数f(x)=lg.
(1)求证:f(x)是奇函数;
(2)求证:f(x)+f(y)=f;
(3)若f=1,f=2,求f(a),f(b)的值.
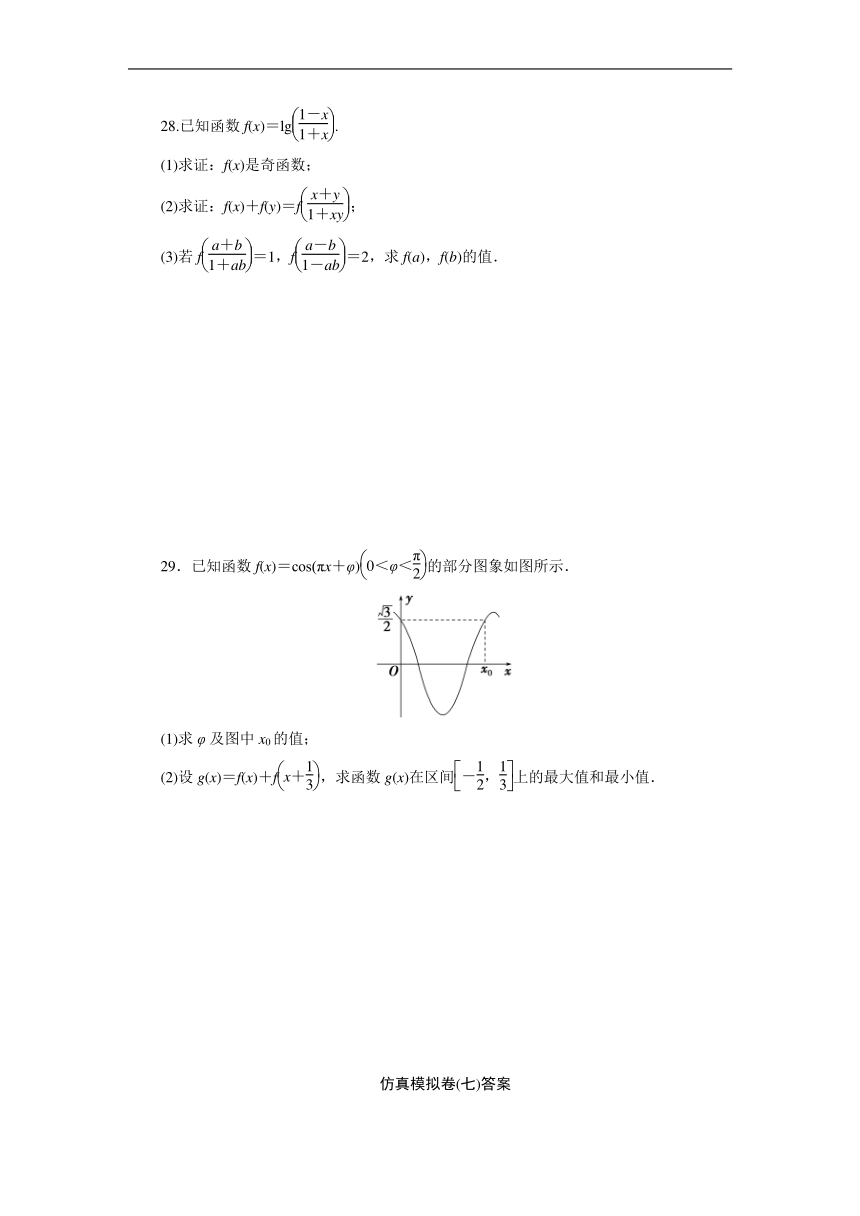
29.已知函数f(x)=cos(πx+φ)的部分图象如图所示.
(1)求φ及图中x0的值;
(2)设g(x)=f(x)+f,求函数g(x)在区间上的最大值和最小值.
仿真模拟卷(七)答案
1.解析:选A 在数轴上表示出集合A,B,如图所示.
由图知A∩B={x|-2<x<-1}.
2.解析:选A 若x为自然数,则它必为整数,即p q.
但x为整数不一定是自然数,如x=-2,即q / p.故p是q的充分不必要条件.
3.解析:选D 根据题意得,用分层随机抽样在各层中的抽样比为=,
则高二年级抽取的人数是300×=30(人).
4.解析:选A 由复数的运算法则,可得
====-1-i,
结合题意可得a+bi=-1-i,即a=-1,b=-1,据此可得a+b=-2.故选A.
5.解析:选D 将这组数据按从小到大排列得
85 87 88 89 89 90 91 91 92 93 93 93 94 96 98
则15×60%=9,15×90%=13.5,
所以60%分位数为=92.5,90%分位数为96.
6.解析:选B 由正弦定理得,a==.
7.解析:选D ∵正四棱柱的底面边长为1,侧棱长为,∴正四棱柱体对角线的长为=2.又∵正四棱柱的顶点在同一球面上,∴正四棱柱体对角线恰好是球的一条直径,得球的半径R=1,根据球的体积公式,得此球的体积V=πR3=,故选D.
8.解析:选D 当a=0时,满足条件;当a≠0时,由题意知a>0且Δ=a2-4a≤0,得0<a≤4,所以0≤a≤4.
9.解析:选C 因为x>0,y>0,x+2y=2,
所以x+2y≥2,即2≥2,xy≤,
当且仅当x=2y,即x=1,y=时,等号成立.
所以xy有最大值,且最大值为.
10.解析:选D ∵|a-b|2=|a|2+|b|2-2a·b
=12+22-2a·b=4.
∴a·b=,
∵|a+b|2=|a-b|2+4a·b=22+4×
=4+2=6,
∴|a+b|2=6,∴|a+b|=.
11.解析:选B
函数f(x)=x-的零点个数是方程x-=0的解的个数,即方程x=的解的个数,也就是函数y=x与y=的图象的交点个数,在同一坐标系中作出两个函数的图象如图所示,可得交点个数为1.
12.解析:选A 甲、乙两个人进行“剪子、包袱、锤”的游戏,所以可能出现的样本点列表如下:
甲
乙 锤 剪子 包袱
锤 (锤,锤) (锤,剪子) (锤,包袱)
剪子 (剪子,锤) (剪子,剪子) (剪子,包袱)
包袱 (包袱,锤) (包袱,剪子) (包袱,包袱)
因为由表格可知,共有9个样本点.
其中平局的有3种,(锤,锤),(剪子,剪子),(包袱,包袱).
设事件A为“甲和乙平局”,则P(A)==.
13.D
14.解析:选C 如图,
||=||=2,〈,〉=60°,
∵D,E是边BC的两个三等分点,
∴·=·=·
=||2+·+||2=×4+×2×2×+×4=.
15.解析:选D 由余弦定理得,b2+c2-a2=2bccos A,a=1,
所以b2+c2-1=2bccos A,
又因为S=bcsin A,4S=b2+c2-1,所以有4×bcsin A=2bccos A,
即sin A=cos A,tan A=1,又因为0由正弦定理得,==2R(R为△ABC外接圆的半径),得R=,
所以△ABC外接圆的面积为.
16.解析:选C ①y=sin,图象的对称中心为,k∈Z,对称轴为x=+kπ,k∈Z,单调递增区间为,k∈Z,最小正周期为2π;②y=sin 2x图象的对称中心为,k∈Z,对称轴为x=+kπ,k∈Z,单调递增区间为,k∈Z,最小正周期为π.故选C.
17.解析:设a与b的夹角为θ,根据题意,可得b·(a+2b)=0,即|a|·|b|cos θ+2b2=0,代入|a|=4|b|,得到cos θ=-,于是a与b的夹角为.
答案:
18.解析:由题意可得,x+y=20,(x-10)2+(y-10)2=8,
设x=10+t,y=10-t,则2t2=8,解得t=±2,∴|x-y|=2|t|=4.
答案:4
19.解析:当t=0.5时,y=2,所以2=e,
所以k=2ln 2,所以y=e2tln 2,
当t=5时,y=e10ln 2=210=1 024.
答案:1 024
20.解析:因为sin(π-α)=,
所以sin α=.因为0<α<,所以cos α==.
因为cos(α-β)=,且0<β<α<,所以0<α-β<,
所以sin(α-β)==,
所以cos β=cos[α-(α-β)]=cos αcos(α-β)+sin αsin(α-β)=×+×=.因为0<β<,所以β=.
答案:
21.解析:∵c2=2b2(1-sin C),∴sin C=1-,
又∵a=b,由余弦定理可得,cos C==1-=sin C,
∴tan C=1,∵C∈(0,π),∴C=.
答案:
22.解析:由题意得EH是△ABD的中位线,∴EH∥BD且EH=BD=3,
又∵==,∴GF∥BD且GF=BD=4,
由基本事实4知,EH∥GF,
∴四边形EFGH是梯形,而直线EH,FG之间的距离就是梯形EFGH的高,设为h,
即=28,得h=8.
答案:8
23.解析:设甲、乙、丙三人击中飞机为事件A,B,C,依题意,A,B,C相互独立,故所求事件概率为P=[P(A)+P(B)+P(C)]×0.2+[P(AB)+P(BC)+P(AC)]
×0.6+P(ABC) =(0.4×0.5×0.2+0.6×0.5×0.2+0.6×0.5×0.8)×0.2+(0.4×0.5×0.2+0.6×0.5×0.8+0.4×0.5×0.8)×0.6+0.4×0.5×0.8=0.492.
答案:0.492
24.解:由0<α<,0<β<,知0<α+β<π,
又因为cos(α+β)=-,所以sin(α+β)===.
由sin α=,可知cos α===,
∴sin β=sin[(α+β)-α]=sin(α+β)cos α-cos(α+β)sin α=×-×=,
又∵β是锐角∴β=.
25.解析:(1)由向量的数量积的运算公式,
可得a·b=|a||b|cos 120°=4×8×=-16,
|a+b|===4.
(2)因为(a+2b)⊥(ka-b),
所以(a+2b)·(ka-b)=ka2-2b2+(2k-1)a·b=0,
整理得16k-128+(2k-1)×(-16)=0,解得k=-7.
即当k=-7时,(a+2b)⊥(ka-b).
26.解析:(1)设“当罚金定为100元时,某员工迟到”为事件A,则P(A)==,
不处罚时,某员工迟到的概率为=.
∴当罚金定为100元时,比不进行处罚员工迟到的概率会降低.
(2)由题意知,A类员工和B类员工各有40人,分别从A类员工和B类员工各抽出两人,
设从A类员工抽出的两人分别为A1,A2,从B类员工抽出的两人分别为B1,B2,
设“从A类与B类员工按分层随机抽样的方法抽取4人依次进行深度问卷调查”为事件M,
则事件M中首先抽出A1的样本点有(A1,A2,B1,B2),(A1,A2,B2,B1),(A1,B1,A2,B2),(A1,B1,B2,A2),(A1,B2,A2,B1),(A1,B2,B1,A2),共6个,
同理,首先抽出A2,B1,B2的样本点也各有6个,故事件M共有4×6=24(个)样本点.
设“抽取4人中前两位均为B类员工”为事件N,则事件N有(B1,B2,A1,A2),(B1,B2,A2,A1),(B2,B1,A1,A2),(B2,B1,A2,A1),共4个样本点.
∴P(N)==,
∴抽取4人中前两位均为B类员工的概率是.
27.证明:(1)因为在△BCD中,点E,F分别是BD,BC的中点,
所以EF∥CD,
又因为EF 平面ACD,CD 平面ACD,所以EF∥平面ACD.
(2)因为点E是BD的中点,且AB=AD,所以AE⊥BD,
又因为AE⊥BC,BC 平面BCD,BD 平面BCD.
BC∩BD=B,所以AE⊥平面BCD,
又因为CD 平面BCD,
所以AE⊥CD.
28.(1)证明:由函数f(x)=lg,可得>0,即<0,解得-1(2)证明:f(x)+f(y)=lg+lg=lg
而f=lg=lg=lg,
∴f(x)+f(y)=f成立.
(3)解:若f=1,f=2,
则由(2)可得f(a)+f(b)=1,f(a)-f(b)=2,解得f(a)=,f(b)=-.
29.解析:(1)由题图得f(0)=,所以cos φ=,
因为0<φ<,故φ=.
因为f(x)的最小正周期等于2,所以由题图可知1<x0<2,
所以<πx0+<.
由f(x0)=,得cos=,所以πx0+=,x0=.
(2)因为f=cos=cos πx+=-sin πx,
所以g(x)=f(x)+f=cos-sin πx=cos πxcos-sin πxsin-sin πx
=cos πx-sin πx=sin.
当x∈时,-≤-πx≤.
所以-≤sin≤1,
所以-≤sin≤,
即-≤g(x)≤.
故-πx=,即x=-时,
g(x)取得最大值;
当-πx=-,即x=时,g(x)取得最小值-.
数学仿真模拟卷(七)
一、选择题(本大题共16小题,每题3分,共48分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.若集合A={x|-2<x<1},B={x |x<-1或x>3},则A∩B=( )
A.{x|-2<x<-1} B.{x|-2<x<3} C.{x|-1<x<1} D.{x|1<x<3}
2.已知命题p:x为自然数,命题q:x为整数,则p是q的( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
3.某学校有高中学生1 000人,其中高一年级、高二年级、高三年级的人数分别为320,300,380.为调查学生参加“社区志愿服务”的意向,现采用分层随机抽样的方法从中抽取一个容量为100的样本,那么应抽取高二年级学生的人数为( )
A.68 B.38 C.32 D.30
4.已知复数a+bi= (i是虚数单位,a,b∈R),则a+b等于( )
A.-2 B.-1 C.0 D.2
5.某校高一年级15个班参加朗诵比赛的得分如下:
91 89 90 92 94 87 93 96 91 85 89 93 88 98 93
则这组数据的60%分位数、90%分位数分别为( )
A.92,96 B.93,96 C.92.5,95 D.92.5,96
6.在△ABC中,若A=60°,C=45°,c=,则a等于( )
A.1 B. C. D.2
7.已知底面边长为1,侧棱长为的正四棱柱的各顶点均在同一球面上,则该球的体积为( )
A. B.4π C.2π D.
8.若集合A={x|ax2-ax+1<0}= ,则实数a的取值范围是( )
A.(0,4) B.[0,4) C.(0,4] D.[0,4]
9.已知x>0,y>0,且x+2y=2,则xy( )
A.有最大值为1 B.有最小值为1 C.有最大值为 D.有最小值为
10.已知向量a,b满足|a|=1,|b|=2,|a-b|=2,则|a+b|等于( )
A.1 B. C. D.
11.函数f(x)=x-的零点个数是( )
A.0 B.1 C.2 D.3
12.甲、乙两个人进行“剪子、包袱、锤”的游戏,两人都随机出拳,则一次游戏两人平局的概率为( )
A. B. C. D.
13.“十一”期间,高速公路车辆较多.某调查公司在一服务区从七座以下小型汽车中抽取了40名驾驶员进行询问调查,将他们在某段高速公路的车速(km/h)分成六段:[60,65),[65,70),[70,75),[75,80),[80,85),[85,90],得到如图所示的频率分布直方图.下列结论错误的是( )
A.这40辆小型汽车车速的众数的估计值为77.5
B.在该服务区任意抽取一辆车,车速超过80 km/h的概率为0.35
C.若从车速在[60,70)的车辆中任意抽取2辆,则至少有一辆车的车速在[65,70)的概率为
D.若从车速在[60,70)的车辆中任意抽取2辆,则车速都在[60,65)内的概率为
14.设D,E为正三角形ABC中BC边上的两个三等分点,且BC=2,则·等于( )
A. B. C. D.
15.在△ABC中,内角A,B,C的对边分别为a,b,c.若△ABC的面积为S,且a=1,4S=b2+c2-1,则△ABC外接圆的面积为( )
A.4π B.2π C.π D.
16.已知函数①y=sin x+cos x,②y=2sin xcos x,则下列结论正确的是( )
A.两个函数的图象均关于点成中心对称图形
B.两个函数的图象均关于直线x=-成轴对称图形
C.两个函数在区间上都是单调递增函数
D.两个函数的最小正周期相同
二、填空题(本大题共7小题,每小题3分,共21分)
17.已知非零向量a,b满足|a|=4|b|,且b⊥(a+2b),则a与b的夹角为________.
18.某人5次上班途中所花的时间(单位:分钟)分别为x,y,10,11,9.已知这组数据的平均数为10,方差为2,则|x-y|的值为________.
19.某种病毒经30分钟繁殖为原来的2倍,且知病毒的繁殖规律为y=ekt(其中k为常数,t表示时间,单位:小时,y表示病毒个数),则经过5小时,1个病毒能繁殖为________个.
20.已知sin(π-α)=,cos(α-β)=,0<β<α<,角β的大小为________.
21.在△ABC中,角A,B,C的对边分别是a,b,c,已知a=b,c2=2b2(1-sin C),则C=________.
22.如图所示,在空间四边形ABCD中,E,H分别是AB,AD的中点,F,G分别是CB,CD上的点,且==,若BD=6,四边形EFGH的面积为28,则直线EH,FG之间的距离为________.
23.甲、乙、丙三人向同一飞机射击,设击中的概率分别为0.4,0.5,0.8,若只有1人击中,则飞机被击落的概率为0.2,若2人击中,则飞机被击落的概率为0.6,若3人击中,则飞机一定被击落,则飞机被击落的概率为________.
三、解答题(本大题共6小题,共31分,解答应写出文字说明、证明过程或演算步骤)
24.设α,β是锐角,sin α=,cos(α+β)=-,求β的值.
25.已知|a|=4,|b|=8,a与b的夹角是120°.
(1)求a·b的值及|a+b|的值;
(2)当k为何值时,(a+2b)⊥(ka-b)
26.某集团公司为了加强企业管理,树立企业形象,考虑在公司内部对迟到现象进行处罚,现在员工中随机抽取200人进行调查,当不处罚时,有80人迟到,处罚时,得到如下数据:
处罚金额x(单位:元) 50 100 150 200
迟到的人数y 50 40 20 0
若用表中数据所得频率代替概率.
(1)当处罚金额定为100元时,员工迟到的概率会比不进行处罚时降低多少?
(2)将选取的200人中会迟到的员工分为A,B两类:A类员工在罚金不超过100元时就会改正行为;B类是其他员工.现对A类与B类员工按分层随机抽样的方法抽取4人依次进行深度问卷调查,则前两位均为B类员工的概率是多少?
27.如图,在三棱锥A BCD中,点E,F分别是BD,BC的中点,AB=AD,AE⊥BC.
求证:(1)EF∥平面ACD;
(2)AE⊥CD.
28.已知函数f(x)=lg.
(1)求证:f(x)是奇函数;
(2)求证:f(x)+f(y)=f;
(3)若f=1,f=2,求f(a),f(b)的值.
29.已知函数f(x)=cos(πx+φ)的部分图象如图所示.
(1)求φ及图中x0的值;
(2)设g(x)=f(x)+f,求函数g(x)在区间上的最大值和最小值.
仿真模拟卷(七)答案
1.解析:选A 在数轴上表示出集合A,B,如图所示.
由图知A∩B={x|-2<x<-1}.
2.解析:选A 若x为自然数,则它必为整数,即p q.
但x为整数不一定是自然数,如x=-2,即q / p.故p是q的充分不必要条件.
3.解析:选D 根据题意得,用分层随机抽样在各层中的抽样比为=,
则高二年级抽取的人数是300×=30(人).
4.解析:选A 由复数的运算法则,可得
====-1-i,
结合题意可得a+bi=-1-i,即a=-1,b=-1,据此可得a+b=-2.故选A.
5.解析:选D 将这组数据按从小到大排列得
85 87 88 89 89 90 91 91 92 93 93 93 94 96 98
则15×60%=9,15×90%=13.5,
所以60%分位数为=92.5,90%分位数为96.
6.解析:选B 由正弦定理得,a==.
7.解析:选D ∵正四棱柱的底面边长为1,侧棱长为,∴正四棱柱体对角线的长为=2.又∵正四棱柱的顶点在同一球面上,∴正四棱柱体对角线恰好是球的一条直径,得球的半径R=1,根据球的体积公式,得此球的体积V=πR3=,故选D.
8.解析:选D 当a=0时,满足条件;当a≠0时,由题意知a>0且Δ=a2-4a≤0,得0<a≤4,所以0≤a≤4.
9.解析:选C 因为x>0,y>0,x+2y=2,
所以x+2y≥2,即2≥2,xy≤,
当且仅当x=2y,即x=1,y=时,等号成立.
所以xy有最大值,且最大值为.
10.解析:选D ∵|a-b|2=|a|2+|b|2-2a·b
=12+22-2a·b=4.
∴a·b=,
∵|a+b|2=|a-b|2+4a·b=22+4×
=4+2=6,
∴|a+b|2=6,∴|a+b|=.
11.解析:选B
函数f(x)=x-的零点个数是方程x-=0的解的个数,即方程x=的解的个数,也就是函数y=x与y=的图象的交点个数,在同一坐标系中作出两个函数的图象如图所示,可得交点个数为1.
12.解析:选A 甲、乙两个人进行“剪子、包袱、锤”的游戏,所以可能出现的样本点列表如下:
甲
乙 锤 剪子 包袱
锤 (锤,锤) (锤,剪子) (锤,包袱)
剪子 (剪子,锤) (剪子,剪子) (剪子,包袱)
包袱 (包袱,锤) (包袱,剪子) (包袱,包袱)
因为由表格可知,共有9个样本点.
其中平局的有3种,(锤,锤),(剪子,剪子),(包袱,包袱).
设事件A为“甲和乙平局”,则P(A)==.
13.D
14.解析:选C 如图,
||=||=2,〈,〉=60°,
∵D,E是边BC的两个三等分点,
∴·=·=·
=||2+·+||2=×4+×2×2×+×4=.
15.解析:选D 由余弦定理得,b2+c2-a2=2bccos A,a=1,
所以b2+c2-1=2bccos A,
又因为S=bcsin A,4S=b2+c2-1,所以有4×bcsin A=2bccos A,
即sin A=cos A,tan A=1,又因为0
所以△ABC外接圆的面积为.
16.解析:选C ①y=sin,图象的对称中心为,k∈Z,对称轴为x=+kπ,k∈Z,单调递增区间为,k∈Z,最小正周期为2π;②y=sin 2x图象的对称中心为,k∈Z,对称轴为x=+kπ,k∈Z,单调递增区间为,k∈Z,最小正周期为π.故选C.
17.解析:设a与b的夹角为θ,根据题意,可得b·(a+2b)=0,即|a|·|b|cos θ+2b2=0,代入|a|=4|b|,得到cos θ=-,于是a与b的夹角为.
答案:
18.解析:由题意可得,x+y=20,(x-10)2+(y-10)2=8,
设x=10+t,y=10-t,则2t2=8,解得t=±2,∴|x-y|=2|t|=4.
答案:4
19.解析:当t=0.5时,y=2,所以2=e,
所以k=2ln 2,所以y=e2tln 2,
当t=5时,y=e10ln 2=210=1 024.
答案:1 024
20.解析:因为sin(π-α)=,
所以sin α=.因为0<α<,所以cos α==.
因为cos(α-β)=,且0<β<α<,所以0<α-β<,
所以sin(α-β)==,
所以cos β=cos[α-(α-β)]=cos αcos(α-β)+sin αsin(α-β)=×+×=.因为0<β<,所以β=.
答案:
21.解析:∵c2=2b2(1-sin C),∴sin C=1-,
又∵a=b,由余弦定理可得,cos C==1-=sin C,
∴tan C=1,∵C∈(0,π),∴C=.
答案:
22.解析:由题意得EH是△ABD的中位线,∴EH∥BD且EH=BD=3,
又∵==,∴GF∥BD且GF=BD=4,
由基本事实4知,EH∥GF,
∴四边形EFGH是梯形,而直线EH,FG之间的距离就是梯形EFGH的高,设为h,
即=28,得h=8.
答案:8
23.解析:设甲、乙、丙三人击中飞机为事件A,B,C,依题意,A,B,C相互独立,故所求事件概率为P=[P(A)+P(B)+P(C)]×0.2+[P(AB)+P(BC)+P(AC)]
×0.6+P(ABC) =(0.4×0.5×0.2+0.6×0.5×0.2+0.6×0.5×0.8)×0.2+(0.4×0.5×0.2+0.6×0.5×0.8+0.4×0.5×0.8)×0.6+0.4×0.5×0.8=0.492.
答案:0.492
24.解:由0<α<,0<β<,知0<α+β<π,
又因为cos(α+β)=-,所以sin(α+β)===.
由sin α=,可知cos α===,
∴sin β=sin[(α+β)-α]=sin(α+β)cos α-cos(α+β)sin α=×-×=,
又∵β是锐角∴β=.
25.解析:(1)由向量的数量积的运算公式,
可得a·b=|a||b|cos 120°=4×8×=-16,
|a+b|===4.
(2)因为(a+2b)⊥(ka-b),
所以(a+2b)·(ka-b)=ka2-2b2+(2k-1)a·b=0,
整理得16k-128+(2k-1)×(-16)=0,解得k=-7.
即当k=-7时,(a+2b)⊥(ka-b).
26.解析:(1)设“当罚金定为100元时,某员工迟到”为事件A,则P(A)==,
不处罚时,某员工迟到的概率为=.
∴当罚金定为100元时,比不进行处罚员工迟到的概率会降低.
(2)由题意知,A类员工和B类员工各有40人,分别从A类员工和B类员工各抽出两人,
设从A类员工抽出的两人分别为A1,A2,从B类员工抽出的两人分别为B1,B2,
设“从A类与B类员工按分层随机抽样的方法抽取4人依次进行深度问卷调查”为事件M,
则事件M中首先抽出A1的样本点有(A1,A2,B1,B2),(A1,A2,B2,B1),(A1,B1,A2,B2),(A1,B1,B2,A2),(A1,B2,A2,B1),(A1,B2,B1,A2),共6个,
同理,首先抽出A2,B1,B2的样本点也各有6个,故事件M共有4×6=24(个)样本点.
设“抽取4人中前两位均为B类员工”为事件N,则事件N有(B1,B2,A1,A2),(B1,B2,A2,A1),(B2,B1,A1,A2),(B2,B1,A2,A1),共4个样本点.
∴P(N)==,
∴抽取4人中前两位均为B类员工的概率是.
27.证明:(1)因为在△BCD中,点E,F分别是BD,BC的中点,
所以EF∥CD,
又因为EF 平面ACD,CD 平面ACD,所以EF∥平面ACD.
(2)因为点E是BD的中点,且AB=AD,所以AE⊥BD,
又因为AE⊥BC,BC 平面BCD,BD 平面BCD.
BC∩BD=B,所以AE⊥平面BCD,
又因为CD 平面BCD,
所以AE⊥CD.
28.(1)证明:由函数f(x)=lg,可得>0,即<0,解得-1
而f=lg=lg=lg,
∴f(x)+f(y)=f成立.
(3)解:若f=1,f=2,
则由(2)可得f(a)+f(b)=1,f(a)-f(b)=2,解得f(a)=,f(b)=-.
29.解析:(1)由题图得f(0)=,所以cos φ=,
因为0<φ<,故φ=.
因为f(x)的最小正周期等于2,所以由题图可知1<x0<2,
所以<πx0+<.
由f(x0)=,得cos=,所以πx0+=,x0=.
(2)因为f=cos=cos πx+=-sin πx,
所以g(x)=f(x)+f=cos-sin πx=cos πxcos-sin πxsin-sin πx
=cos πx-sin πx=sin.
当x∈时,-≤-πx≤.
所以-≤sin≤1,
所以-≤sin≤,
即-≤g(x)≤.
故-πx=,即x=-时,
g(x)取得最大值;
当-πx=-,即x=时,g(x)取得最小值-.
同课章节目录
