27.2 相似三角形 同步练习(含答案) 2022-2023学年人教版九年级下册数学
文档属性
| 名称 | 27.2 相似三角形 同步练习(含答案) 2022-2023学年人教版九年级下册数学 |

|
|
| 格式 | zip | ||
| 文件大小 | 232.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-23 00:00:00 | ||
图片预览


文档简介
27.2 相似三角形 同步练习
一、单选题
1.如图,取一张长为a,宽为b的长方形纸片,将它对折两次后得到一张小长方形纸片,若要使小长方形与原长方形相似,则原长方形纸片的边a、b应满足的条件是( )
A.a= b B.a=2b C.a=2 b D.a=4b
2.如图,△ABC中,点D是AB上一点,补充下列条件后,仍不能判定△ADC∽△ACB的是( )
A.∠ADC=∠ACB B.∠ACD=∠ABC
C. = D. =
3.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,如果AC=3,AB=6,那么AD的值为( )
A. B. C. D.3
4.如图,正方形ABCD的边长是3,BP=CQ,连接AQ,DP交于点O,并分别与边CD,BC交于点F,E,连接AE,下列结论:①AQ⊥DP;②OA2=OE OP;③S△AOD=S四边形OECF;④当BP=1时,tan∠OAE= ,其中正确结论的个数是( )
A.1 B.2 C.3 D.4
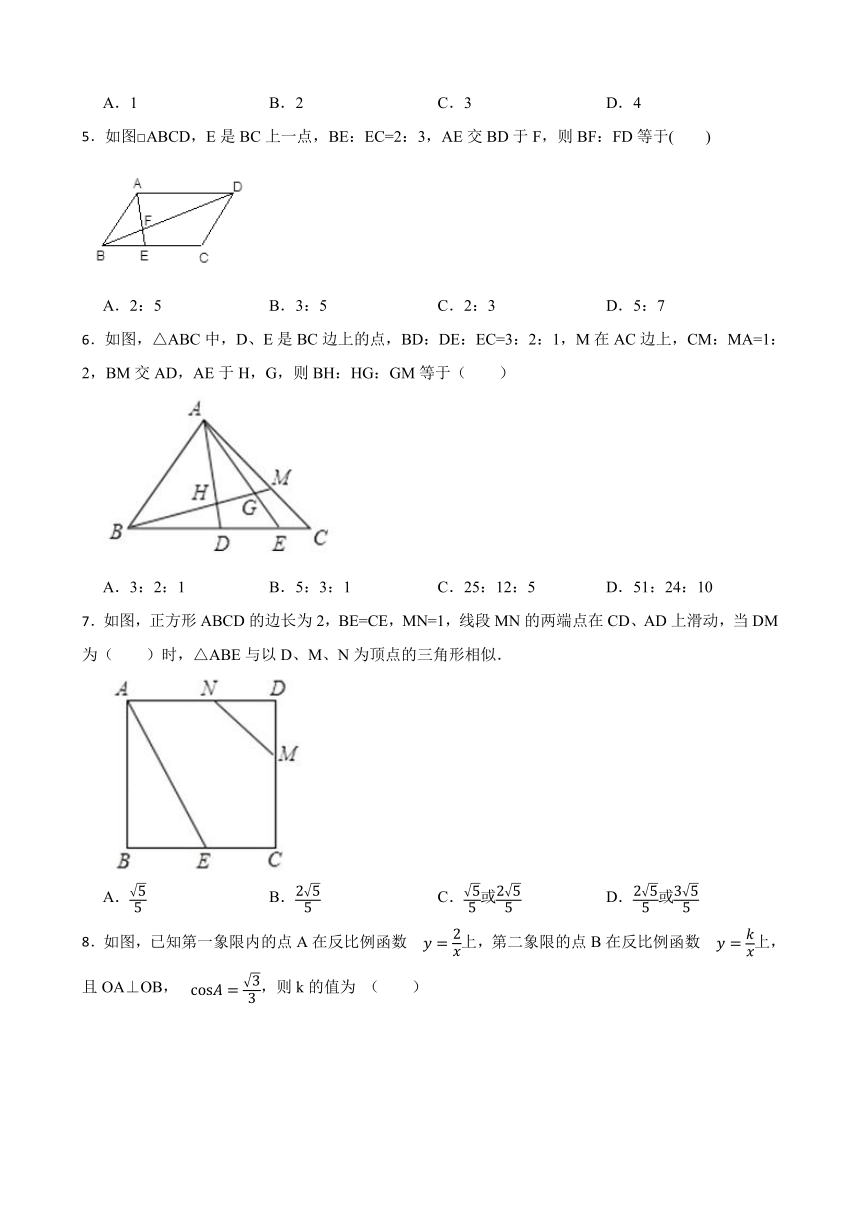
5.如图□ABCD,E是BC上一点,BE:EC=2:3,AE交BD于F,则BF:FD等于( )
A.2:5 B.3:5 C.2:3 D.5:7
6.如图,△ABC中,D、E是BC边上的点,BD:DE:EC=3:2:1,M在AC边上,CM:MA=1:2,BM交AD,AE于H,G,则BH:HG:GM等于( )
A.3:2:1 B.5:3:1 C.25:12:5 D.51:24:10
7.如图,正方形ABCD的边长为2,BE=CE,MN=1,线段MN的两端点在CD、AD上滑动,当DM为( )时,△ABE与以D、M、N为顶点的三角形相似.
A. B. C.或 D.或
8.如图,已知第一象限内的点A在反比例函数
上,第二象限的点B在反比例函数
上,且OA⊥OB,
,则k的值为 ( )
A.-3
B.-6
C.-4
D.
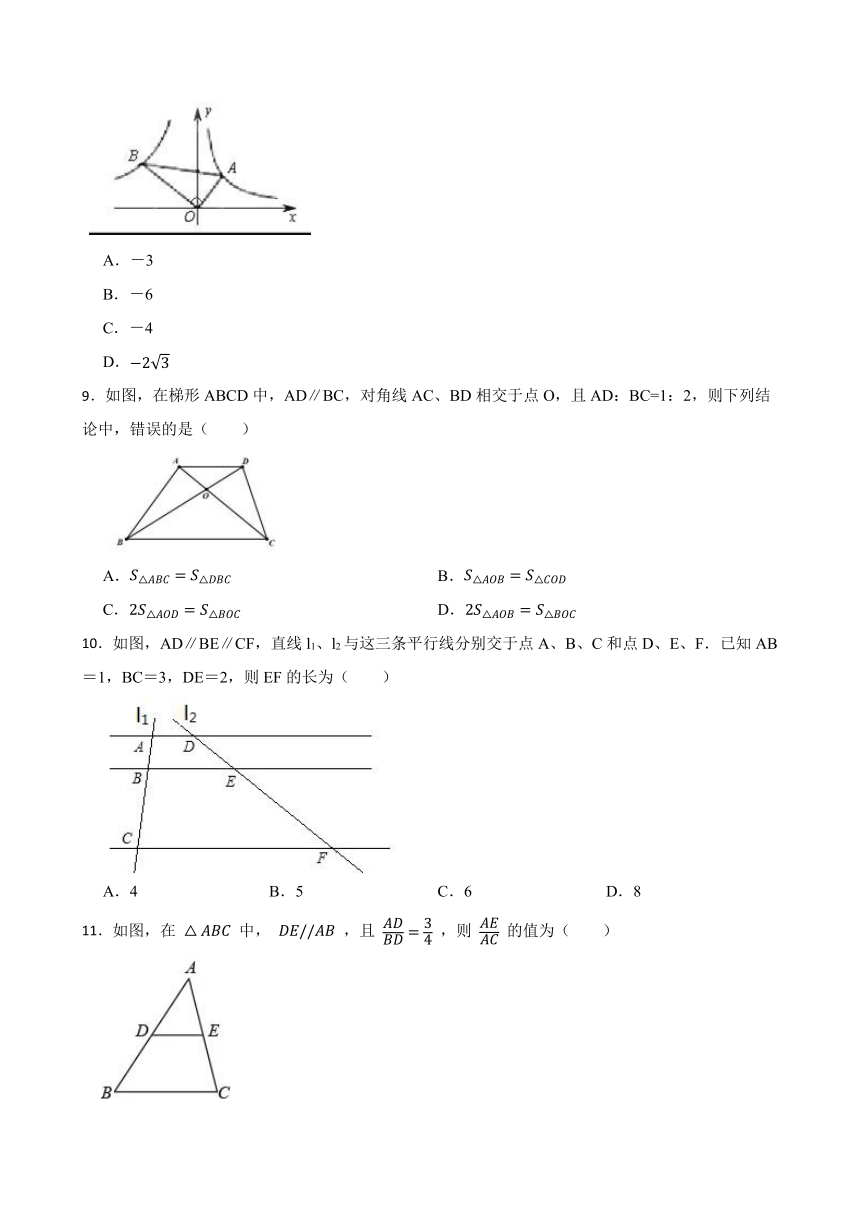
9.如图,在梯形ABCD中,AD∥BC,对角线AC、BD相交于点O,且AD:BC=1:2,则下列结论中,错误的是( )
A. B.
C. D.
10.如图,AD∥BE∥CF,直线l1、l2与这三条平行线分别交于点A、B、C和点D、E、F.已知AB=1,BC=3,DE=2,则EF的长为( )
A.4 B.5 C.6 D.8
11.如图,在 中, ,且 ,则 的值为( )
A. B. C. D.
12.如图.直线l1∥l2∥l3,直线AC分别交l1,l2,l3于点A,B,C;直线DF分别交l1,l2,l3于点D,E,F;AC与DF相交于点H,且AH=4,HB=2,BC=10,则 =( )
A. B.2 C. D.
二、填空题
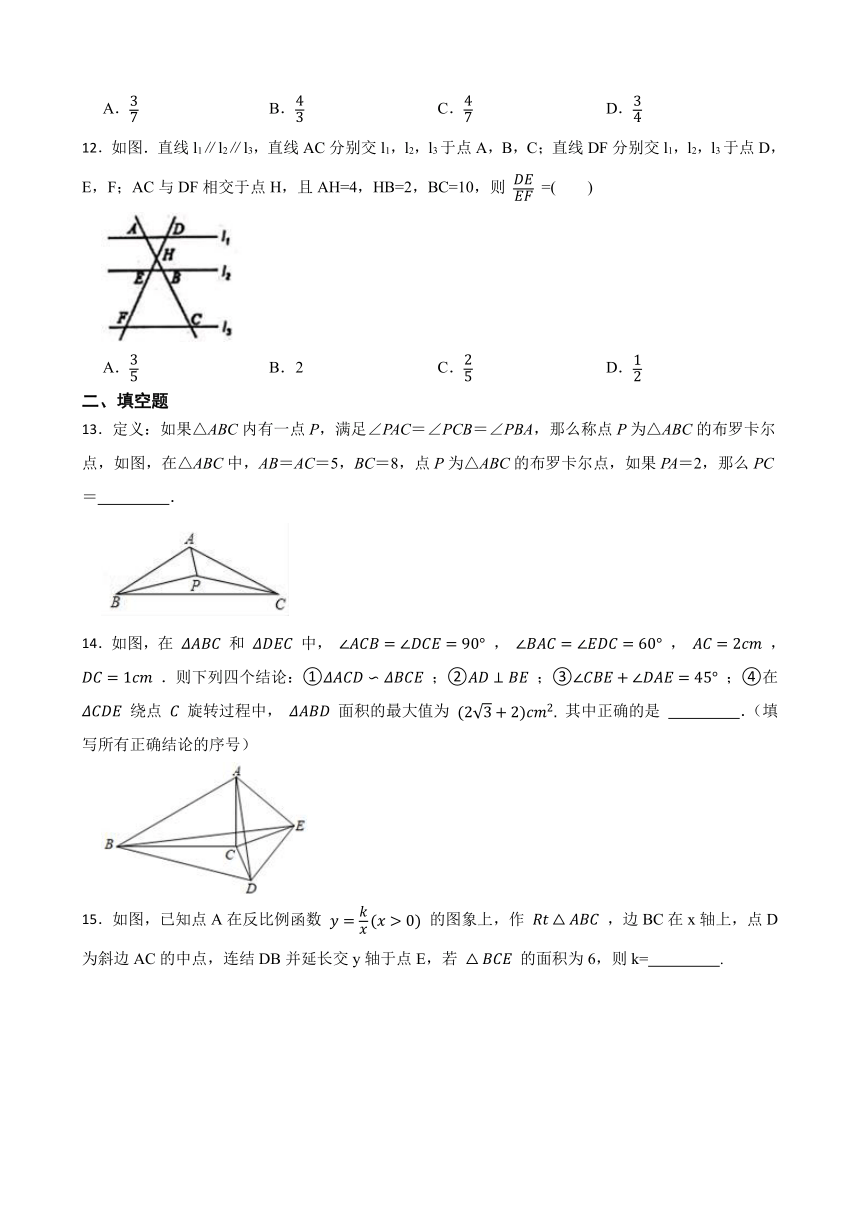
13.定义:如果△ABC内有一点P,满足∠PAC=∠PCB=∠PBA,那么称点P为△ABC的布罗卡尔点,如图,在△ABC中,AB=AC=5,BC=8,点P为△ABC的布罗卡尔点,如果PA=2,那么PC= .
14.如图,在 和 中, , , , .则下列四个结论:① ;② ;③ ;④在 绕点 旋转过程中, 面积的最大值为 其中正确的是 .(填写所有正确结论的序号)
15.如图,已知点A在反比例函数 的图象上,作 ,边BC在x轴上,点D为斜边AC的中点,连结DB并延长交y轴于点E,若 的面积为6,则k= .
16.已知在△ABC中,点D、E分别在边AB、AC上,DE//BC,=,那么的值等于 .
17.如图,在 中,∠C=90°,AC=3,BC=4,把 绕C点旋转得到 ,其中点 在线段AB上,那么 的正切值等于
18.如果两个相似三角形的对应边上的高之比是2:3,则它们的周长比是
三、综合题
19.阅读下列材料,完成任务
小明同学酷爱数学,勤于探索研究,他画了一个三角形ABC,并画出其中一个外角 的角平分线,与BC的延长线交于点N,小明通过测量发现,该图形中的线段有特殊的关系: ,他想证明自己的发现.下面是部分证明过程:
证明:过点C作 交AB于点D,则 (第一步),
∴ , (第二步)
…
请回答下面问题:
(1)小明部分证明过程中,第一步的依据是 ;
(2)请完成证明的剩余部分;
(3)若 , , ,请求出CN的长.
20.如图,在Rt△ABC中,∠BAC=90°,AB=6,AC=8,点D为边BC的中点,点P为射线AB上的一动点,点Q为边AC上的一动点,且∠PDQ=90°.
(1)当DP⊥AB时,求CQ的长;
(2)当BP=2,求CQ的长
21.如图所示,Rt△ABC中,已知∠BAC=90°,AB=AC=2,点D在BC上运动(不能到达点B,C),过点D作∠ADE=45°,DE交AC于点E.
(1)求证:△ABD∽△DCE;
(2)当△ADE是等腰三角形时,求AE的长.
22.如图,已知抛物线经过A(﹣2,0)B(﹣3,3)及原点O,顶点为C.
(1)求抛物线的解析式;
(2)若点E在抛物线的对称轴上,且A、O、D、E为顶点是四边形是平行四边形,求点D的坐标.
(3)P是抛物线上的第一象限内的动点,过点P作PM⊥x轴,垂足为M,是否存在点P,使得以P、M、A为顶点的三角形△BOC相似?
23.如图,在△ABC中,AB=AC=6,BC=2,过点A作AM∥BC,点P是AB上一点,作∠CPD=∠B,PD交AM于点D。
(1)如图8-1,在BA的延长线上取点G,使得DG=DA,则 的值为 ;
(2)如图8-1,在(1)的条件下,求证:△DGP∽△PBC
;
(3)如图8-2,当点P是AB的中点时,求AD的长。
24.如图,已知 , , , , .
(1)求 和 的大小;
(2)求 的长
答案解析部分
1.【答案】B
2.【答案】D
3.【答案】A
4.【答案】C
5.【答案】C
6.【答案】D
7.【答案】C
8.【答案】B
9.【答案】C
10.【答案】C
11.【答案】A
12.【答案】A
13.【答案】
14.【答案】①②④
15.【答案】12
16.【答案】
17.【答案】
18.【答案】2:3
19.【答案】(1)平行线分线段成比例定理
(2)证明:∵ 平分 ,
∴ ,
∴ ,
∴ ,
∴ ;
(3)解:过点 作 于点 ,
∵ , ,
∴ , ,
∵ ,
∴ ,即 为 的中点,
∴ 为等腰三角形,
∴ ,
∵ ,即 ,
解得: .
20.【答案】(1)解:如图,
∵ DP⊥AB ,∠BAC=90°,∠PDQ=90°.
∴∠BAC=∠PDQ=∠APD=90°
∴四边形APDQ是矩形,
∴DQ⊥AC,
∴∠DQC=∠BAC=90°,
∴DQ∥AB,
∵点D是BC的中点,
∴CQ=AQ=AC=×8=4.
(2)解:∵如图,当点P在线段AB上时,作DM⊥AB,DN⊥AC,垂足分别为M、N,
易证四边形AMDN是矩形,DM、DN分别是△ABC的中位线,DM=4,DN=3,
∵∠PDQ=∠MDN=90°,
∴∠PDM=∠QDN,
∵∠DNQ∠DMP=90°,
∴△PDM∽△QDN,
∴PM:QN=DM:DN=4:3,
∴QN=PM,
∵PM=BM PB=3 2=1,
∴QN=,
∴CQ=QN+CN=+4=;
如图,当点P在AB的延长线上时,
同理可证△PDM∽△QDN,DM=4,DN=3
∴PM:QN=DM:DN=4:3,
∴QN=PM,
∵PM=BM+PB=3+2=5,
∴QN=,
∴CQ=QN+CN=;
∴当BP=2,求CQ的长为或.
21.【答案】(1)证明:Rt△ABC中,∠BAC=90°,AB=AC=2,
∴∠B=∠C=45°.
∵∠ADC=∠B+∠BAD,∠ADC=∠ADE+∠EDC,
∴∠ADE+∠EDC=∠B+∠BAD.
又∵∠ADE=45°,
∴45°+∠EDC=45°+∠BAD.
∴∠EDC=∠BAD.
∴△ABD∽△DCE.
(2)解:讨论:①若AD=AE时,∠DAE=90°,此时D点与点B重合,不合题意.
②若AD=DE时,△ABD与△DCE的相似比为1,此时△ABD≌△DCE,
于是AB=AC=2,BC=2 ,AE=AC﹣EC=2﹣BD=2﹣(2 ﹣2)=4﹣2
③若AE=DE,此时∠DAE=∠ADE=45°,
如下图所示易知AD⊥BC,DE⊥AC,且AD=DC.由等腰三角形的三线合一可知:AE=CE= AC=1.
22.【答案】(1)解:设抛物线的解析式为y=ax2+bx+c(a≠0),
将点A(﹣2,0),B(﹣3,3),O(0,0),代入可得:
,
解得: ,
所以函数解析式为:y=x2+2x
(2)解:①以AE为边时,∵A,O,D,E为顶点的四边形是平行四边形,
∴DE=AO=2,D在x轴向方不可能,
∴D在x轴上方,且DE=2,当D点在对称轴直线x=﹣1的右侧时,D的坐标为(1,3);
当D点在对称轴直线x=﹣1的左侧时,根据二次函数图象的对称性可知点D的坐标为(﹣3,3),
②以AO为对角线时,则DE与AO互相平分,
∵点E在对称轴上,且线段AO的中点横坐标为﹣1,
由对称性可知,符合条件的点D只有一个,与点C重合,即C(﹣1,﹣1),
综上点D的坐标为(1,3)或(﹣3,3)(﹣1,﹣1)
(3)解:假设存在点P,使以P,M,A为顶点的三角形与△BOC相似,如图 ,
设P(x,y),由题意知x>0,y>0,且y=x2+2x,
由题意,△BOC为直角三角形,∠COB=90°,且OC:OB=1:3,
①若△PMA∽△COB,则 = ,
即x+2=3(x2+2x),得
x1= ,x2=﹣2(舍去),当x= 时,y= ,即P( , );
②若△PMA∽△BOC, = ,
即:x2+2x=3(x+2),
得:x1=3,x2=﹣2(舍去)当x=3时,y=15,即P(3,15)
故符合条件的点P有两个,分别( , )或(3,15)
23.【答案】(1)3
(2)证明: (如图1)
∵∠APC=∠GPD+∠DPC ,
∠APC=∠B+∠BCP,
又∠CPD=∠B,
∴∠GPD=∠BCP
又AD=DG,
∴∠G=∠GAD
又AM∥BC,
∴∠GAD=∠B,
∴∠G=∠B.
又∠GPD=∠BCP
∴△DGP∽△PBC
(3)解:(如图2)
在BA的延长线上取点G,使得DA= DG
∵AB=AC,DA=DG,
∴∠ACB=∠B,∠G=∠GAD.
∵AM∥BC,
∵∠GAD=∠B.
∴∠G=∠ACB .
∴△DGA∽△ACB
∴
∴
又点P是AB的中点,
∴AP=BP=3
设AD=x,则DG=x,AG= x,PG=3+ x,
由(2)得△DGP△PBC,
∴
∴
解得x=9
∴AD=9
24.【答案】(1)解: ,
,
,
,
,
, .
(2)解: ,
∴ ,
∵ , , ,
∴ ,
∴ .
一、单选题
1.如图,取一张长为a,宽为b的长方形纸片,将它对折两次后得到一张小长方形纸片,若要使小长方形与原长方形相似,则原长方形纸片的边a、b应满足的条件是( )
A.a= b B.a=2b C.a=2 b D.a=4b
2.如图,△ABC中,点D是AB上一点,补充下列条件后,仍不能判定△ADC∽△ACB的是( )
A.∠ADC=∠ACB B.∠ACD=∠ABC
C. = D. =
3.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,如果AC=3,AB=6,那么AD的值为( )
A. B. C. D.3
4.如图,正方形ABCD的边长是3,BP=CQ,连接AQ,DP交于点O,并分别与边CD,BC交于点F,E,连接AE,下列结论:①AQ⊥DP;②OA2=OE OP;③S△AOD=S四边形OECF;④当BP=1时,tan∠OAE= ,其中正确结论的个数是( )
A.1 B.2 C.3 D.4
5.如图□ABCD,E是BC上一点,BE:EC=2:3,AE交BD于F,则BF:FD等于( )
A.2:5 B.3:5 C.2:3 D.5:7
6.如图,△ABC中,D、E是BC边上的点,BD:DE:EC=3:2:1,M在AC边上,CM:MA=1:2,BM交AD,AE于H,G,则BH:HG:GM等于( )
A.3:2:1 B.5:3:1 C.25:12:5 D.51:24:10
7.如图,正方形ABCD的边长为2,BE=CE,MN=1,线段MN的两端点在CD、AD上滑动,当DM为( )时,△ABE与以D、M、N为顶点的三角形相似.
A. B. C.或 D.或
8.如图,已知第一象限内的点A在反比例函数
上,第二象限的点B在反比例函数
上,且OA⊥OB,
,则k的值为 ( )
A.-3
B.-6
C.-4
D.
9.如图,在梯形ABCD中,AD∥BC,对角线AC、BD相交于点O,且AD:BC=1:2,则下列结论中,错误的是( )
A. B.
C. D.
10.如图,AD∥BE∥CF,直线l1、l2与这三条平行线分别交于点A、B、C和点D、E、F.已知AB=1,BC=3,DE=2,则EF的长为( )
A.4 B.5 C.6 D.8
11.如图,在 中, ,且 ,则 的值为( )
A. B. C. D.
12.如图.直线l1∥l2∥l3,直线AC分别交l1,l2,l3于点A,B,C;直线DF分别交l1,l2,l3于点D,E,F;AC与DF相交于点H,且AH=4,HB=2,BC=10,则 =( )
A. B.2 C. D.
二、填空题
13.定义:如果△ABC内有一点P,满足∠PAC=∠PCB=∠PBA,那么称点P为△ABC的布罗卡尔点,如图,在△ABC中,AB=AC=5,BC=8,点P为△ABC的布罗卡尔点,如果PA=2,那么PC= .
14.如图,在 和 中, , , , .则下列四个结论:① ;② ;③ ;④在 绕点 旋转过程中, 面积的最大值为 其中正确的是 .(填写所有正确结论的序号)
15.如图,已知点A在反比例函数 的图象上,作 ,边BC在x轴上,点D为斜边AC的中点,连结DB并延长交y轴于点E,若 的面积为6,则k= .
16.已知在△ABC中,点D、E分别在边AB、AC上,DE//BC,=,那么的值等于 .
17.如图,在 中,∠C=90°,AC=3,BC=4,把 绕C点旋转得到 ,其中点 在线段AB上,那么 的正切值等于
18.如果两个相似三角形的对应边上的高之比是2:3,则它们的周长比是
三、综合题
19.阅读下列材料,完成任务
小明同学酷爱数学,勤于探索研究,他画了一个三角形ABC,并画出其中一个外角 的角平分线,与BC的延长线交于点N,小明通过测量发现,该图形中的线段有特殊的关系: ,他想证明自己的发现.下面是部分证明过程:
证明:过点C作 交AB于点D,则 (第一步),
∴ , (第二步)
…
请回答下面问题:
(1)小明部分证明过程中,第一步的依据是 ;
(2)请完成证明的剩余部分;
(3)若 , , ,请求出CN的长.
20.如图,在Rt△ABC中,∠BAC=90°,AB=6,AC=8,点D为边BC的中点,点P为射线AB上的一动点,点Q为边AC上的一动点,且∠PDQ=90°.
(1)当DP⊥AB时,求CQ的长;
(2)当BP=2,求CQ的长
21.如图所示,Rt△ABC中,已知∠BAC=90°,AB=AC=2,点D在BC上运动(不能到达点B,C),过点D作∠ADE=45°,DE交AC于点E.
(1)求证:△ABD∽△DCE;
(2)当△ADE是等腰三角形时,求AE的长.
22.如图,已知抛物线经过A(﹣2,0)B(﹣3,3)及原点O,顶点为C.
(1)求抛物线的解析式;
(2)若点E在抛物线的对称轴上,且A、O、D、E为顶点是四边形是平行四边形,求点D的坐标.
(3)P是抛物线上的第一象限内的动点,过点P作PM⊥x轴,垂足为M,是否存在点P,使得以P、M、A为顶点的三角形△BOC相似?
23.如图,在△ABC中,AB=AC=6,BC=2,过点A作AM∥BC,点P是AB上一点,作∠CPD=∠B,PD交AM于点D。
(1)如图8-1,在BA的延长线上取点G,使得DG=DA,则 的值为 ;
(2)如图8-1,在(1)的条件下,求证:△DGP∽△PBC
;
(3)如图8-2,当点P是AB的中点时,求AD的长。
24.如图,已知 , , , , .
(1)求 和 的大小;
(2)求 的长
答案解析部分
1.【答案】B
2.【答案】D
3.【答案】A
4.【答案】C
5.【答案】C
6.【答案】D
7.【答案】C
8.【答案】B
9.【答案】C
10.【答案】C
11.【答案】A
12.【答案】A
13.【答案】
14.【答案】①②④
15.【答案】12
16.【答案】
17.【答案】
18.【答案】2:3
19.【答案】(1)平行线分线段成比例定理
(2)证明:∵ 平分 ,
∴ ,
∴ ,
∴ ,
∴ ;
(3)解:过点 作 于点 ,
∵ , ,
∴ , ,
∵ ,
∴ ,即 为 的中点,
∴ 为等腰三角形,
∴ ,
∵ ,即 ,
解得: .
20.【答案】(1)解:如图,
∵ DP⊥AB ,∠BAC=90°,∠PDQ=90°.
∴∠BAC=∠PDQ=∠APD=90°
∴四边形APDQ是矩形,
∴DQ⊥AC,
∴∠DQC=∠BAC=90°,
∴DQ∥AB,
∵点D是BC的中点,
∴CQ=AQ=AC=×8=4.
(2)解:∵如图,当点P在线段AB上时,作DM⊥AB,DN⊥AC,垂足分别为M、N,
易证四边形AMDN是矩形,DM、DN分别是△ABC的中位线,DM=4,DN=3,
∵∠PDQ=∠MDN=90°,
∴∠PDM=∠QDN,
∵∠DNQ∠DMP=90°,
∴△PDM∽△QDN,
∴PM:QN=DM:DN=4:3,
∴QN=PM,
∵PM=BM PB=3 2=1,
∴QN=,
∴CQ=QN+CN=+4=;
如图,当点P在AB的延长线上时,
同理可证△PDM∽△QDN,DM=4,DN=3
∴PM:QN=DM:DN=4:3,
∴QN=PM,
∵PM=BM+PB=3+2=5,
∴QN=,
∴CQ=QN+CN=;
∴当BP=2,求CQ的长为或.
21.【答案】(1)证明:Rt△ABC中,∠BAC=90°,AB=AC=2,
∴∠B=∠C=45°.
∵∠ADC=∠B+∠BAD,∠ADC=∠ADE+∠EDC,
∴∠ADE+∠EDC=∠B+∠BAD.
又∵∠ADE=45°,
∴45°+∠EDC=45°+∠BAD.
∴∠EDC=∠BAD.
∴△ABD∽△DCE.
(2)解:讨论:①若AD=AE时,∠DAE=90°,此时D点与点B重合,不合题意.
②若AD=DE时,△ABD与△DCE的相似比为1,此时△ABD≌△DCE,
于是AB=AC=2,BC=2 ,AE=AC﹣EC=2﹣BD=2﹣(2 ﹣2)=4﹣2
③若AE=DE,此时∠DAE=∠ADE=45°,
如下图所示易知AD⊥BC,DE⊥AC,且AD=DC.由等腰三角形的三线合一可知:AE=CE= AC=1.
22.【答案】(1)解:设抛物线的解析式为y=ax2+bx+c(a≠0),
将点A(﹣2,0),B(﹣3,3),O(0,0),代入可得:
,
解得: ,
所以函数解析式为:y=x2+2x
(2)解:①以AE为边时,∵A,O,D,E为顶点的四边形是平行四边形,
∴DE=AO=2,D在x轴向方不可能,
∴D在x轴上方,且DE=2,当D点在对称轴直线x=﹣1的右侧时,D的坐标为(1,3);
当D点在对称轴直线x=﹣1的左侧时,根据二次函数图象的对称性可知点D的坐标为(﹣3,3),
②以AO为对角线时,则DE与AO互相平分,
∵点E在对称轴上,且线段AO的中点横坐标为﹣1,
由对称性可知,符合条件的点D只有一个,与点C重合,即C(﹣1,﹣1),
综上点D的坐标为(1,3)或(﹣3,3)(﹣1,﹣1)
(3)解:假设存在点P,使以P,M,A为顶点的三角形与△BOC相似,如图 ,
设P(x,y),由题意知x>0,y>0,且y=x2+2x,
由题意,△BOC为直角三角形,∠COB=90°,且OC:OB=1:3,
①若△PMA∽△COB,则 = ,
即x+2=3(x2+2x),得
x1= ,x2=﹣2(舍去),当x= 时,y= ,即P( , );
②若△PMA∽△BOC, = ,
即:x2+2x=3(x+2),
得:x1=3,x2=﹣2(舍去)当x=3时,y=15,即P(3,15)
故符合条件的点P有两个,分别( , )或(3,15)
23.【答案】(1)3
(2)证明: (如图1)
∵∠APC=∠GPD+∠DPC ,
∠APC=∠B+∠BCP,
又∠CPD=∠B,
∴∠GPD=∠BCP
又AD=DG,
∴∠G=∠GAD
又AM∥BC,
∴∠GAD=∠B,
∴∠G=∠B.
又∠GPD=∠BCP
∴△DGP∽△PBC
(3)解:(如图2)
在BA的延长线上取点G,使得DA= DG
∵AB=AC,DA=DG,
∴∠ACB=∠B,∠G=∠GAD.
∵AM∥BC,
∵∠GAD=∠B.
∴∠G=∠ACB .
∴△DGA∽△ACB
∴
∴
又点P是AB的中点,
∴AP=BP=3
设AD=x,则DG=x,AG= x,PG=3+ x,
由(2)得△DGP△PBC,
∴
∴
解得x=9
∴AD=9
24.【答案】(1)解: ,
,
,
,
,
, .
(2)解: ,
∴ ,
∵ , , ,
∴ ,
∴ .
