9.2.2多边形的内角和[下学期]
文档属性
| 名称 | 9.2.2多边形的内角和[下学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 319.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-05-23 07:37:00 | ||
图片预览




文档简介
课件18张PPT。§9.2.2多边形的内角和巩固复习问题1:
三角形的内角和、外角和分别是多少? 问题2:
长方形、正方形的内角和分别是多少? 问题3:
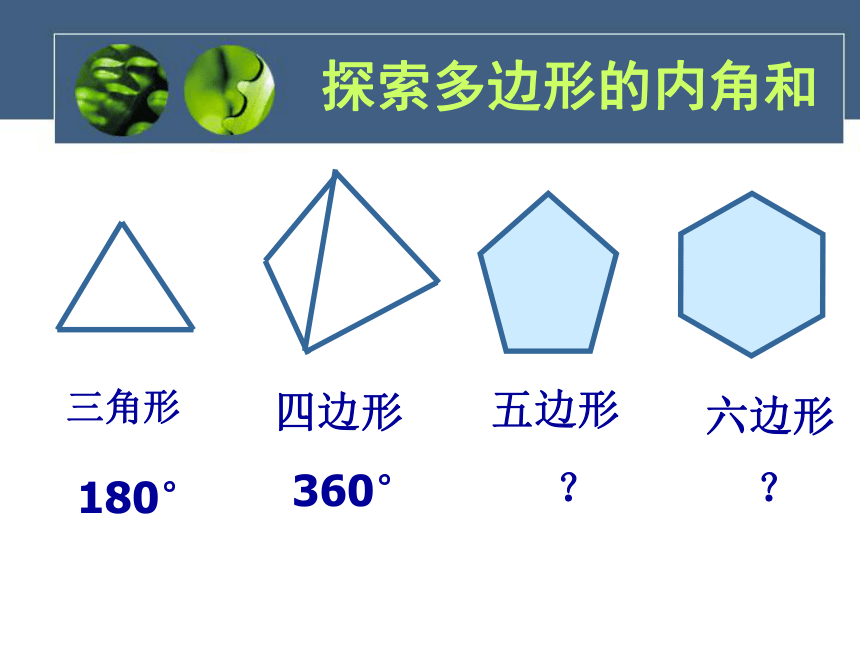
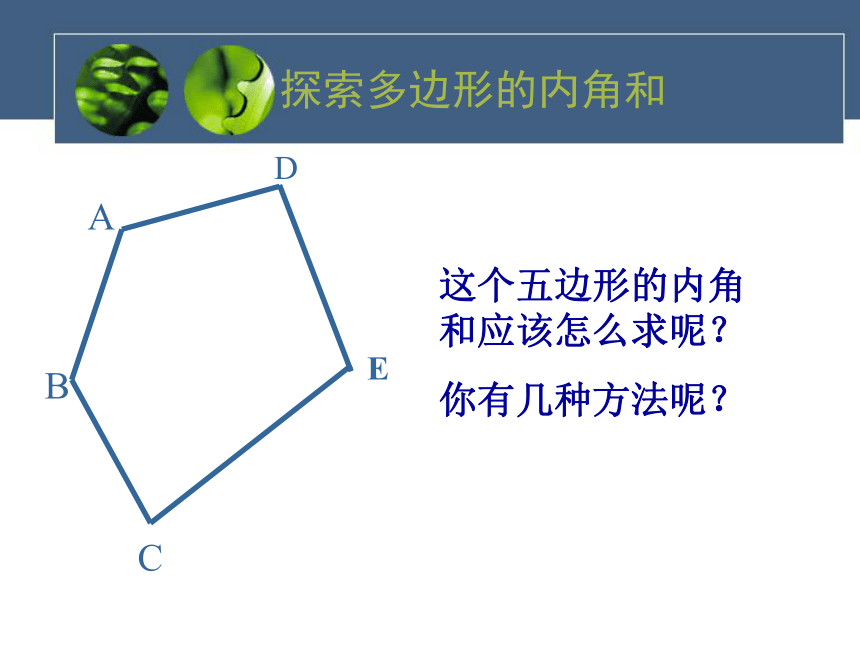
四边形的内角和是多少?四边形内角和为180.三角形 六边形 四边形探索多边形的内角和五边形180°360°??做一做你能仿照四边形求内角和的方法,求出五边形、六边形的的内角和吗? 那n边形呢? 探索多边形的内角和这个五边形的内角和应该怎么求呢?
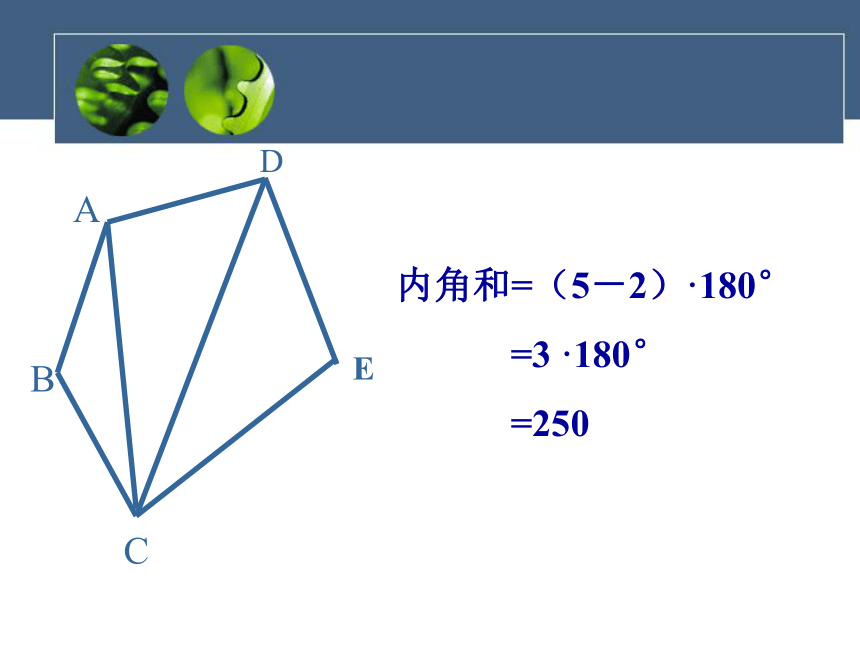
你有几种方法呢?ACDEB内角和=(5-2)·180°
=3 ·180°
=250探索多边形的内角和这种探索方法你掌握了吗?请完成下表345n-2900 °(n-2) ×1800720 °540 °n 边形的内角和为:(n-2)×180°ACDEBO内角和=4×180°-180°
= 3×180°
=380°探索多边形的内角和456n-1900 °(n-1) ×180 0
-1800720 °540 °n 边形的内角和为:(n-1)×180°-1800ACDEBO内角和=5×180°-360 °=540 °
=3×180°
探索多边形的内角和567 n900 °1800×n-3600720 °540 °n 边形的内角和为:180°×n-3600总结n边形内角和为(n-2)×1800五边形180°360°540°n边形1.快速抢答 (1)8边形内角和是_______°, (2)32边形内角和是________°, (3)一个多边形的内角和是1440°, 它是_____边形。应用知识解决问题(1)10540010802.多边形外角与内角之间有什么关系?应用知识解决问题(1)各内角与相邻外角互补;(1)外角和=n个平角-内角和
=n×180°-(n-2) × 180°=360°(2)结论:n边形的外角和等于360°3.多边形的外角和是多少?探究1.小明想:2008年奥运会在北京召开,设计一个内角和为2008?的多边形图案多有意义,小明的想法能实现吗?课时小结通过本节课的学习,你学到了哪些知识?有何体会?(1)这节课我们主要学习了多边形的内角和公式:(n-2)×180?;
(2)多边形的外角和为:3600作业选择适当的多边形拼一幅美丽的地面的图案。
三角形的内角和、外角和分别是多少? 问题2:
长方形、正方形的内角和分别是多少? 问题3:
四边形的内角和是多少?四边形内角和为180.三角形 六边形 四边形探索多边形的内角和五边形180°360°??做一做你能仿照四边形求内角和的方法,求出五边形、六边形的的内角和吗? 那n边形呢? 探索多边形的内角和这个五边形的内角和应该怎么求呢?
你有几种方法呢?ACDEB内角和=(5-2)·180°
=3 ·180°
=250探索多边形的内角和这种探索方法你掌握了吗?请完成下表345n-2900 °(n-2) ×1800720 °540 °n 边形的内角和为:(n-2)×180°ACDEBO内角和=4×180°-180°
= 3×180°
=380°探索多边形的内角和456n-1900 °(n-1) ×180 0
-1800720 °540 °n 边形的内角和为:(n-1)×180°-1800ACDEBO内角和=5×180°-360 °=540 °
=3×180°
探索多边形的内角和567 n900 °1800×n-3600720 °540 °n 边形的内角和为:180°×n-3600总结n边形内角和为(n-2)×1800五边形180°360°540°n边形1.快速抢答 (1)8边形内角和是_______°, (2)32边形内角和是________°, (3)一个多边形的内角和是1440°, 它是_____边形。应用知识解决问题(1)10540010802.多边形外角与内角之间有什么关系?应用知识解决问题(1)各内角与相邻外角互补;(1)外角和=n个平角-内角和
=n×180°-(n-2) × 180°=360°(2)结论:n边形的外角和等于360°3.多边形的外角和是多少?探究1.小明想:2008年奥运会在北京召开,设计一个内角和为2008?的多边形图案多有意义,小明的想法能实现吗?课时小结通过本节课的学习,你学到了哪些知识?有何体会?(1)这节课我们主要学习了多边形的内角和公式:(n-2)×180?;
(2)多边形的外角和为:3600作业选择适当的多边形拼一幅美丽的地面的图案。
