2022-2023学年人教版数学九年级下册 26.1反比例函数同步练习 (含答案)
文档属性
| 名称 | 2022-2023学年人教版数学九年级下册 26.1反比例函数同步练习 (含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 326.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-24 00:00:00 | ||
图片预览


文档简介
26.1反比例函数
(同步练习)
一、单选题
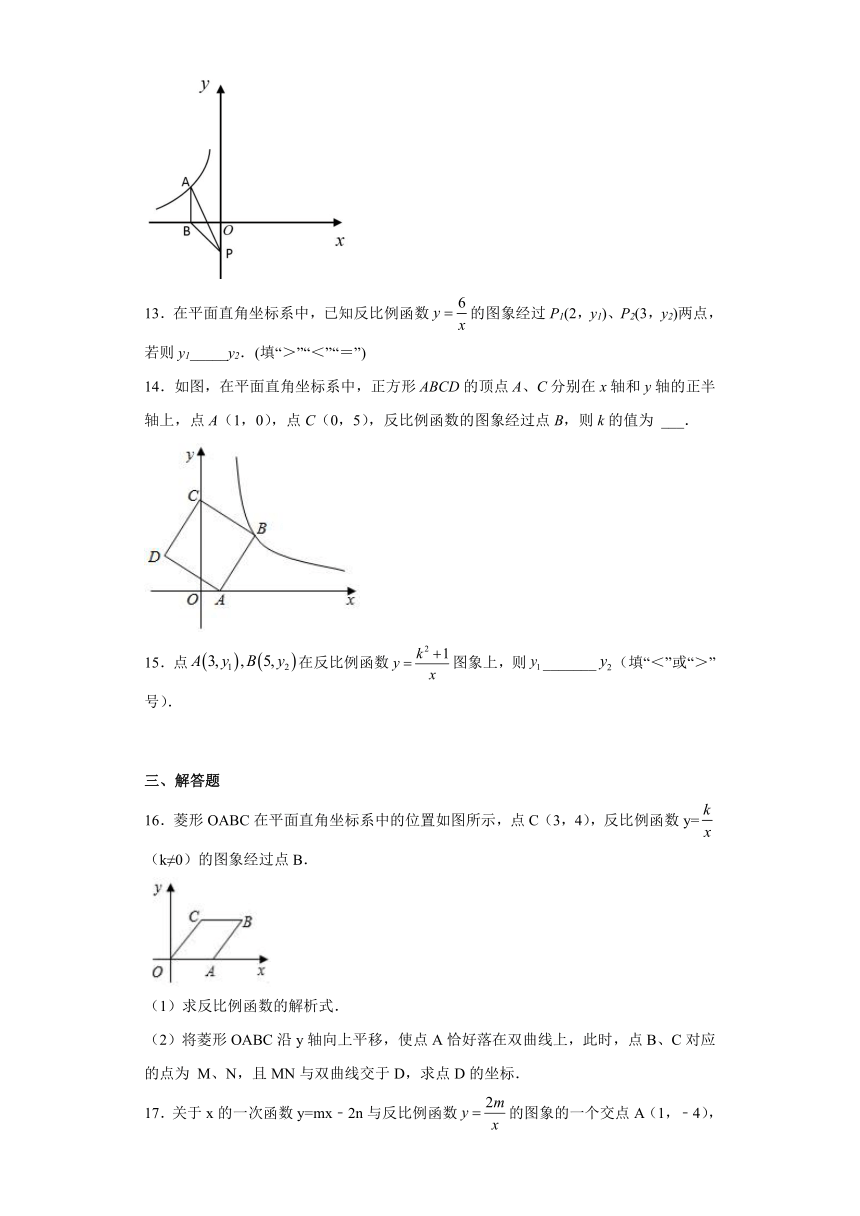
1.如图,已知点是一次函数图像上一点,过点作轴的垂线是上一点(在上方),在的右侧以为斜边作等腰直角三角形,反比例函数的图像过点,若的面积为6,则的面积是 ( )
A. B.4 C.3 D.
2.若、是函数的图象上的两点,且,则与的大小关系为( )
A.bc C.b=c D.无法判断
3.如图,直线l与函数的图像相交,是直线的三点,过点、、分 别作轴的垂线,垂足分别为,连接,设的面积是,的面积是, 的面积是,则( )
A. B. C. D.
4.如图,在平面直角坐标系中,矩形的边、分别在轴和轴上,,,点是边上一动点,过点的反比例函数与边交于点.若将沿折叠,点的对应点恰好落在对角线上. 则反比例函数的解析式是( )
A. B. C. D.
5.下列关于反比例函数的结论中正确的是( )
A.图象过点(1,3) B.图象在一、三象限内
C.当时,y随x的增大而增大 D.当时
6.正比例函数y=2x和反比例函数y都经过的点是( )
A.(0,0) B.(1,2) C.(﹣2,﹣1) D.(2,4)
7.下列函数中,当时,y随x的增大而减小的是( )
A. B. C. D.
8.下列四个点,在反比例函数图象上的是( )
A. B. C. D.
9.反比例函数的图像向下平移1个单位,与轴交点的坐标是( )
A. B. C. D.
10.下列各点中,在反比例函数图象上的点是( )
A. B. C. D.
二、填空题
11.设有反比例函数,(,),(,)为图象上的两点,若,则____ (填“>”、“<”或“=”)
12.如图,是反比例函数图象上的一点,过点作轴于点,点在轴上,的面积为1,则的值为______.
13.在平面直角坐标系中,已知反比例函数的图象经过P1(2,y1)、P2(3,y2)两点,若则y1_____y2.(填“>”“<”“=”)
14.如图,在平面直角坐标系中,正方形ABCD的顶点A、C分别在x轴和y轴的正半轴上,点A(1,0),点C(0,5),反比例函数的图象经过点B,则k的值为 ___.
15.点在反比例函数图象上,则_______(填“<”或“>”号).
三、解答题
16.菱形OABC在平面直角坐标系中的位置如图所示,点C(3,4),反比例函数y=(k≠0)的图象经过点B.
(1)求反比例函数的解析式.
(2)将菱形OABC沿y轴向上平移,使点A恰好落在双曲线上,此时,点B、C对应的点为 M、N,且MN与双曲线交于D,求点D的坐标.
17.关于x的一次函数y=mx﹣2n与反比例函数的图象的一个交点A(1,﹣4),求一次函数和反比例函数的解析式.
18.小明为探究函数的图象和性质,需要画出函数图象,列表如下:
…… ……
…… ……
根据上表数据,在平面直角坐标系中描点,画出函数图象,如图如示,小明画出了图象的一部分.
(1)请你帮小明画出完整的的图象;
(2)观察函数图象,请写出这个函数的两条性质:
性质一: ;
性质二: .
(3)利用上述图象,探究函数图象与直线的关系;
①当 时, 直线与函数在第一象限的图象有一个交点,则的坐标是 ;
②当为何值时,讨论函数的图象与直线的交点个数.
19.如图,为坐标原点,点和点均在反比例函数图像上.
(1)求,的值;
(2)设直线与轴交于点,求的面积.
20.如图,在平面直角坐标系xOy中,正比例函数y= x的图象与反比例函数y=的图象交于点A(m,-2).将直线y= x沿y轴的正方向向上平移交反比例函数y=的图象于点C(4,n),交y轴于点B,连接AB,AC.
(1) k=______;
(2)求直线BC的解析式;
(3)直接写出△ABC的面积.
21.在平面直角坐标系xOy中,直线l与直线 y= -2x关于y轴对称,直线l与反比例函数的图象的一个交点为A(2, m).
(1)试确定反比例函数的表达式;
(2)若过点A的直线与x轴交于点B,且∠ABO=45°,直接写出点B的坐标.
参考答案:
1.C2.B3.C4.C5.C6.B7.A8.A9.D10.C
11. >
12.
13.>
14.9.
15.>
16.(1)反比例函数的解析式为y=;
(2)点D的坐标(,).
17.y=﹣2x﹣2,
18.(1)绘制完整图象如下图:
;
(2)由图象可得:图象有两个分支,分别在第一、第二象限;
图象在第一象限时,y随x的增大而减小,在第二象限时,y随x的增大而增大;
(3)①当x>0时,方程-x+b=,即为-x+b=,
整理得x2-bx+1=0,
∵直线y=-x+b与函数的图象在第一象限只有一个交点,
∴=0,即b2-4=0,
解得b=2,b=-2(不符合题意,舍去),
把b=2代入x2-bx+1=0,
解得x1=x2=1,
故点A的坐标为(1,1);
②∵的k值小于0,
∴图象经过必定经过二、四象限,
∴当x<0时,直线y=-x+b与函数的图象在第二象限只有一个交点,
由①可知,当x>0,b=2时,直线y=-x+b与函数的图象在第一象限只有一个交点,
∴当b=2时,两个函数有两个交点,
结合图象可知当b>2时,两个函数有三个交点,当b<2时,两函数有一个交点,
综上:当b>2时,两个函数有三个交点;当b=2时,两个函数有两个交点当b<2时;两函数有一个交点.
19.(1) m=5,k=5;(2) 15
20.(1)-4
(2)直线BC的解析式为y=-x+3;
(3)S△ABC=6.
21.(1);(2)(6,0)或(-2,0).
(同步练习)
一、单选题
1.如图,已知点是一次函数图像上一点,过点作轴的垂线是上一点(在上方),在的右侧以为斜边作等腰直角三角形,反比例函数的图像过点,若的面积为6,则的面积是 ( )
A. B.4 C.3 D.
2.若、是函数的图象上的两点,且,则与的大小关系为( )
A.b
3.如图,直线l与函数的图像相交,是直线的三点,过点、、分 别作轴的垂线,垂足分别为,连接,设的面积是,的面积是, 的面积是,则( )
A. B. C. D.
4.如图,在平面直角坐标系中,矩形的边、分别在轴和轴上,,,点是边上一动点,过点的反比例函数与边交于点.若将沿折叠,点的对应点恰好落在对角线上. 则反比例函数的解析式是( )
A. B. C. D.
5.下列关于反比例函数的结论中正确的是( )
A.图象过点(1,3) B.图象在一、三象限内
C.当时,y随x的增大而增大 D.当时
6.正比例函数y=2x和反比例函数y都经过的点是( )
A.(0,0) B.(1,2) C.(﹣2,﹣1) D.(2,4)
7.下列函数中,当时,y随x的增大而减小的是( )
A. B. C. D.
8.下列四个点,在反比例函数图象上的是( )
A. B. C. D.
9.反比例函数的图像向下平移1个单位,与轴交点的坐标是( )
A. B. C. D.
10.下列各点中,在反比例函数图象上的点是( )
A. B. C. D.
二、填空题
11.设有反比例函数,(,),(,)为图象上的两点,若,则____ (填“>”、“<”或“=”)
12.如图,是反比例函数图象上的一点,过点作轴于点,点在轴上,的面积为1,则的值为______.
13.在平面直角坐标系中,已知反比例函数的图象经过P1(2,y1)、P2(3,y2)两点,若则y1_____y2.(填“>”“<”“=”)
14.如图,在平面直角坐标系中,正方形ABCD的顶点A、C分别在x轴和y轴的正半轴上,点A(1,0),点C(0,5),反比例函数的图象经过点B,则k的值为 ___.
15.点在反比例函数图象上,则_______(填“<”或“>”号).
三、解答题
16.菱形OABC在平面直角坐标系中的位置如图所示,点C(3,4),反比例函数y=(k≠0)的图象经过点B.
(1)求反比例函数的解析式.
(2)将菱形OABC沿y轴向上平移,使点A恰好落在双曲线上,此时,点B、C对应的点为 M、N,且MN与双曲线交于D,求点D的坐标.
17.关于x的一次函数y=mx﹣2n与反比例函数的图象的一个交点A(1,﹣4),求一次函数和反比例函数的解析式.
18.小明为探究函数的图象和性质,需要画出函数图象,列表如下:
…… ……
…… ……
根据上表数据,在平面直角坐标系中描点,画出函数图象,如图如示,小明画出了图象的一部分.
(1)请你帮小明画出完整的的图象;
(2)观察函数图象,请写出这个函数的两条性质:
性质一: ;
性质二: .
(3)利用上述图象,探究函数图象与直线的关系;
①当 时, 直线与函数在第一象限的图象有一个交点,则的坐标是 ;
②当为何值时,讨论函数的图象与直线的交点个数.
19.如图,为坐标原点,点和点均在反比例函数图像上.
(1)求,的值;
(2)设直线与轴交于点,求的面积.
20.如图,在平面直角坐标系xOy中,正比例函数y= x的图象与反比例函数y=的图象交于点A(m,-2).将直线y= x沿y轴的正方向向上平移交反比例函数y=的图象于点C(4,n),交y轴于点B,连接AB,AC.
(1) k=______;
(2)求直线BC的解析式;
(3)直接写出△ABC的面积.
21.在平面直角坐标系xOy中,直线l与直线 y= -2x关于y轴对称,直线l与反比例函数的图象的一个交点为A(2, m).
(1)试确定反比例函数的表达式;
(2)若过点A的直线与x轴交于点B,且∠ABO=45°,直接写出点B的坐标.
参考答案:
1.C2.B3.C4.C5.C6.B7.A8.A9.D10.C
11. >
12.
13.>
14.9.
15.>
16.(1)反比例函数的解析式为y=;
(2)点D的坐标(,).
17.y=﹣2x﹣2,
18.(1)绘制完整图象如下图:
;
(2)由图象可得:图象有两个分支,分别在第一、第二象限;
图象在第一象限时,y随x的增大而减小,在第二象限时,y随x的增大而增大;
(3)①当x>0时,方程-x+b=,即为-x+b=,
整理得x2-bx+1=0,
∵直线y=-x+b与函数的图象在第一象限只有一个交点,
∴=0,即b2-4=0,
解得b=2,b=-2(不符合题意,舍去),
把b=2代入x2-bx+1=0,
解得x1=x2=1,
故点A的坐标为(1,1);
②∵的k值小于0,
∴图象经过必定经过二、四象限,
∴当x<0时,直线y=-x+b与函数的图象在第二象限只有一个交点,
由①可知,当x>0,b=2时,直线y=-x+b与函数的图象在第一象限只有一个交点,
∴当b=2时,两个函数有两个交点,
结合图象可知当b>2时,两个函数有三个交点,当b<2时,两函数有一个交点,
综上:当b>2时,两个函数有三个交点;当b=2时,两个函数有两个交点当b<2时;两函数有一个交点.
19.(1) m=5,k=5;(2) 15
20.(1)-4
(2)直线BC的解析式为y=-x+3;
(3)S△ABC=6.
21.(1);(2)(6,0)或(-2,0).
