2022-2023学年 华东师大版七年级数学下册7.3三元一次方程组及其解法课后测评(无答案)
文档属性
| 名称 | 2022-2023学年 华东师大版七年级数学下册7.3三元一次方程组及其解法课后测评(无答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 124.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-24 08:37:36 | ||
图片预览


文档简介
7.3三元一次方程组及其解法课后测评
班级:________ 姓名:________
一、单选题(共 10 小题)
1、有甲、乙、丙三种货物,若购甲3件,乙7件,丙1件,共需315元;若购甲4件,乙10件,丙1件,共需420元.现在购买甲、乙、丙各1件,共需( )
A.105元 B.210元 C.170元 D.不能确定
2、某班元旦晚会需要购买甲、乙、丙三种装饰品,若购买甲3件,乙5件,丙1件,共需62元,若购甲4件,乙7件,丙1件共需77元.现在购买甲、乙、丙各一件,共需( )元.
A.31 B.32 C.33 D.34
3、如图,三个天平的托盘中形状相同的物体质量相等.图①、图②所示的两个天平处于平衡状态,要使第三个天平也保持平衡,可在它的右盘中放置( )
A.3个球 B.4个球
C.5个球 D.6个球
4、解方程组,把上面的三元一次方程组消元转化成下面的二元一次方程组,需要经过如下的步骤,请你选出正确的步骤( )
A. B. C. D.
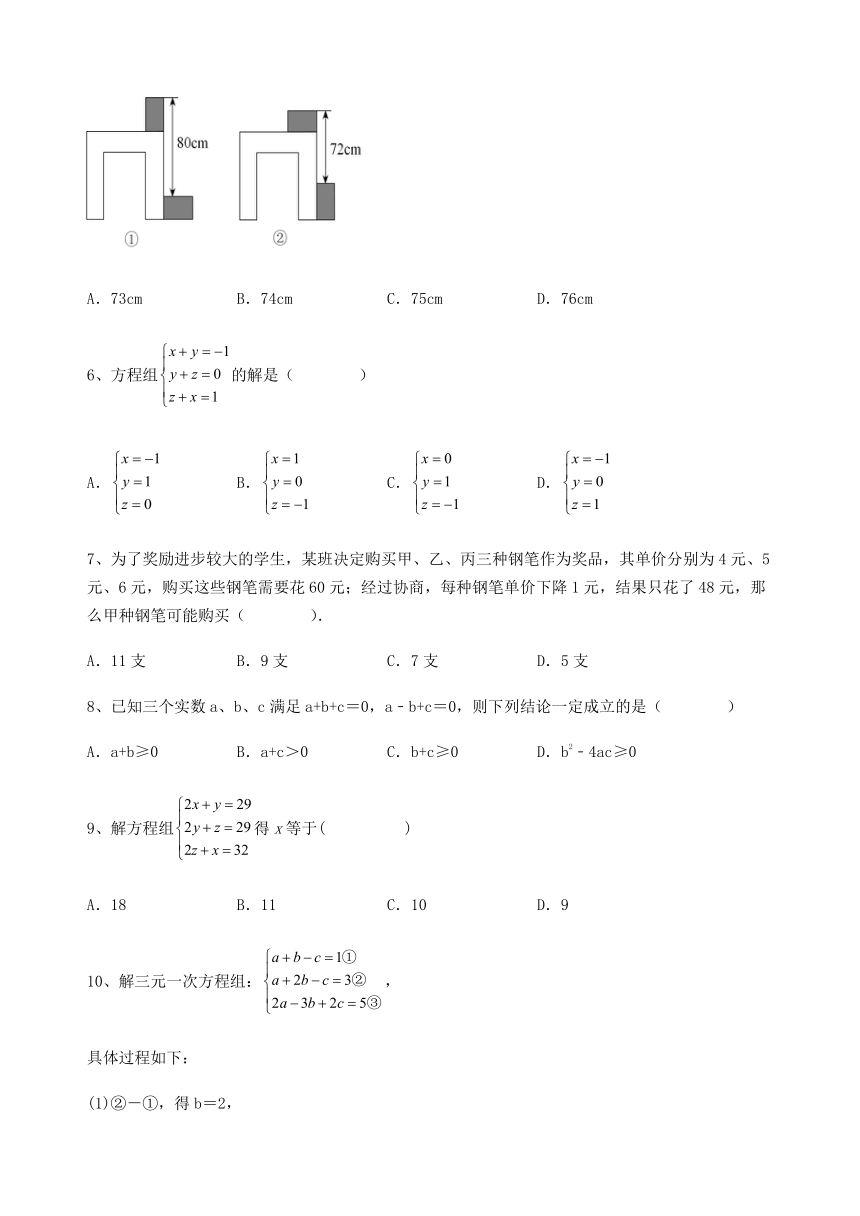
5、利用两块大小一样的长方体木块测量一张桌子的高度,首先按图①方式放置,再交换两木块的位置,按图②方式放置,测量的数据如图,则桌子的高度是( )
A.73cm B.74cm C.75cm D.76cm
6、方程组的解是( )
A. B. C. D.
7、为了奖励进步较大的学生,某班决定购买甲、乙、丙三种钢笔作为奖品,其单价分别为4元、5元、6元,购买这些钢笔需要花60元;经过协商,每种钢笔单价下降1元,结果只花了48元,那么甲种钢笔可能购买( ).
A.11支 B.9支 C.7支 D.5支
8、已知三个实数a、b、c满足a+b+c=0,a﹣b+c=0,则下列结论一定成立的是( )
A.a+b≥0 B.a+c>0 C.b+c≥0 D.b2﹣4ac≥0
9、解方程组得x等于( )
A.18 B.11 C.10 D.9
10、解三元一次方程组:,
具体过程如下:
(1)②-①,得b=2,
(2)①×2+③,得4a-2b=7,
(3)所以,
(4)把b=2代入4a-2b=7,得4a-2×2=7(以下求解过程略).
其中开始出现错误的一步是( )
A.(1) B.(2) C.(3) D.(4)
二、填空题(共 8 小题)
1、甲乙两个同学参加数学比赛,共有选择题、填空题、解答题三种题型.每种题型都不超过10个题,选择题每题3分,填空题每题5分,解答题每题8分,每题除全对外其他情况都不得分,两个同学选择题做对的道数相同,乙做对的填空题比甲做对的填空题至少多2道,甲、乙两个同学每个题型均有做对的题,甲一共得了70分,乙一共得了83分,则两个同学做对的解答题共为________道.
2、山脚下有一池塘,泉水以固定的流量(即单位时间里流入池中的水量相同)不停地向池塘内流淌.现池塘中有一定深度的水,若用一台A型抽水机抽水,则1小时正好能把池塘中的水抽完若用两台A型抽水机抽水,则20分钟正好把池塘中的水抽完.问若用三台A型抽水机同时抽,则需要_____分钟恰好把池塘中的水抽完.
3、小华和小慧到校门外文具店买文件,小华购铅笔2支,练习本2本,圆珠笔1支,共付9元钱;小慧购同样铅笔1支,练习本4本,圆珠笔2支,共付12元钱,若小明去买与她们一样的购铅笔1支、练习本2本、圆珠笔1支,他需付______元钱.
4、如图,为某三岔路口交通环岛的简化模型,在某高峰时刻,单位时间进出路口A,B,C的机动车辆数如图所示.图中分别表示该时段单位时间通过路段AB,BC,CA的机动车辆数.(假设单位时间内在上述路段中同一路段上驶入与驶出的车辆数相等),试比较的大小关系_________.
5、2021新春佳节之际,某商家推出收费印制巴蜀中学logo的新春礼品,礼品主要包含三种:对联,门神和红包,如果印制对联3副、门神2副、红包5个,需付人民币31.5元;如果印制对联2副、门神1副、红包1个,需付人民币22元,某人想印制16副对联、10副门神、22个红包共需付人民币______元.
6、重庆市举行了中学生足球联赛,共赛17轮(即每队均需比赛17场),记分办法是胜一场得3分,平一场得1分,负一场得0分.若文德中学足球队的积分为16分,且踢平场数是所负场数的整数倍,且胜、平、负的场数各不相同.则文德中学足球队共负____场.
7、已知式子,当时,其值为4;当时,其值为8;当时,其值为25;则当时,其值为__________.
8、坐落在北碚区北温泉境内的金刚碑古镇彰显了“一条石板路,千年金刚碑”鲜明的历史和地域特色,为了恢复古镇风貌,打造历史文化街区,政府开始对古镇进行保护性开发,现使用当地甲、乙、丙三种原料生产A、B两种工艺品进行销售.已知制作工艺品A每件需要甲原料1千克,乙原料1千克,丙原料4千克;制作工艺品B每件需要甲原料3千克,乙原料3千克,丙原料2千克.A、B两种工艺品的成本分别等于产品中所含的甲、乙、丙三种原料成本之和.已知每件工艺品B的成本是每千克丙原料成本的8倍,每件工艺品A的利润率是50%,每件工艺品B的利润率是25%,当A、B两种工艺品的销售件数之比是2:1时,求销售这两种工艺品的总销售利润率是_____.
三、解答题(共 6 小题)
1、在中,当x的值分别取1、-1、-2时,的值分别为1、9、19,求a、b、c的值.
2、解方程组:
(1);
(2).
3、已知多项式,当时,它的值是,当时,它的值是,试求的值.
4、阅读感悟:有些关于方程组的问题,欲求结果不是每一个未知数的值,而是关于未知数的代数式的值,如以下问题:
已知实数,满足①,②,求和的值.
本题常规的解题思路是将①,②两式联立组成方程组,解得,的值.再代入欲求值的代数式得到答案,常规思路运算量较大.其实,仔细观察两个方程未知数,的系数与所求代数式中,的系数之间的关系,本题还可以通过适当的变形整体求得代数式的值,由①-②得:,由①+②×2得.这样的解题思想就是通常所说的“整体思想”.
问题解决:
(1)已知二元一次方程组,则的值为______,的值为______.
(2)某班组织活动购买奖品,买5支铅笔、3块橡皮、2本日记本共需32元、买9支铅笔、5块橡皮、3本日记本共需58元,则购买3支铅笔、3块橡皮、3本日记本共需多少元?
(3)对于实数,,定义新运算:,其中,,是常数,等式右边是通常的加法和乘法运算.已知,,求的值.
5、解三元一次方程组:
6、一个手机号前三位数中,中间数字是前面数字的三倍;而第一个数字与第三个数字之和是中间数字的两倍.在后八位数中: 前四位数与后四位数之和是4461;前三位数与后五位数之和是82896.求这个手机号是?
班级:________ 姓名:________
一、单选题(共 10 小题)
1、有甲、乙、丙三种货物,若购甲3件,乙7件,丙1件,共需315元;若购甲4件,乙10件,丙1件,共需420元.现在购买甲、乙、丙各1件,共需( )
A.105元 B.210元 C.170元 D.不能确定
2、某班元旦晚会需要购买甲、乙、丙三种装饰品,若购买甲3件,乙5件,丙1件,共需62元,若购甲4件,乙7件,丙1件共需77元.现在购买甲、乙、丙各一件,共需( )元.
A.31 B.32 C.33 D.34
3、如图,三个天平的托盘中形状相同的物体质量相等.图①、图②所示的两个天平处于平衡状态,要使第三个天平也保持平衡,可在它的右盘中放置( )
A.3个球 B.4个球
C.5个球 D.6个球
4、解方程组,把上面的三元一次方程组消元转化成下面的二元一次方程组,需要经过如下的步骤,请你选出正确的步骤( )
A. B. C. D.
5、利用两块大小一样的长方体木块测量一张桌子的高度,首先按图①方式放置,再交换两木块的位置,按图②方式放置,测量的数据如图,则桌子的高度是( )
A.73cm B.74cm C.75cm D.76cm
6、方程组的解是( )
A. B. C. D.
7、为了奖励进步较大的学生,某班决定购买甲、乙、丙三种钢笔作为奖品,其单价分别为4元、5元、6元,购买这些钢笔需要花60元;经过协商,每种钢笔单价下降1元,结果只花了48元,那么甲种钢笔可能购买( ).
A.11支 B.9支 C.7支 D.5支
8、已知三个实数a、b、c满足a+b+c=0,a﹣b+c=0,则下列结论一定成立的是( )
A.a+b≥0 B.a+c>0 C.b+c≥0 D.b2﹣4ac≥0
9、解方程组得x等于( )
A.18 B.11 C.10 D.9
10、解三元一次方程组:,
具体过程如下:
(1)②-①,得b=2,
(2)①×2+③,得4a-2b=7,
(3)所以,
(4)把b=2代入4a-2b=7,得4a-2×2=7(以下求解过程略).
其中开始出现错误的一步是( )
A.(1) B.(2) C.(3) D.(4)
二、填空题(共 8 小题)
1、甲乙两个同学参加数学比赛,共有选择题、填空题、解答题三种题型.每种题型都不超过10个题,选择题每题3分,填空题每题5分,解答题每题8分,每题除全对外其他情况都不得分,两个同学选择题做对的道数相同,乙做对的填空题比甲做对的填空题至少多2道,甲、乙两个同学每个题型均有做对的题,甲一共得了70分,乙一共得了83分,则两个同学做对的解答题共为________道.
2、山脚下有一池塘,泉水以固定的流量(即单位时间里流入池中的水量相同)不停地向池塘内流淌.现池塘中有一定深度的水,若用一台A型抽水机抽水,则1小时正好能把池塘中的水抽完若用两台A型抽水机抽水,则20分钟正好把池塘中的水抽完.问若用三台A型抽水机同时抽,则需要_____分钟恰好把池塘中的水抽完.
3、小华和小慧到校门外文具店买文件,小华购铅笔2支,练习本2本,圆珠笔1支,共付9元钱;小慧购同样铅笔1支,练习本4本,圆珠笔2支,共付12元钱,若小明去买与她们一样的购铅笔1支、练习本2本、圆珠笔1支,他需付______元钱.
4、如图,为某三岔路口交通环岛的简化模型,在某高峰时刻,单位时间进出路口A,B,C的机动车辆数如图所示.图中分别表示该时段单位时间通过路段AB,BC,CA的机动车辆数.(假设单位时间内在上述路段中同一路段上驶入与驶出的车辆数相等),试比较的大小关系_________.
5、2021新春佳节之际,某商家推出收费印制巴蜀中学logo的新春礼品,礼品主要包含三种:对联,门神和红包,如果印制对联3副、门神2副、红包5个,需付人民币31.5元;如果印制对联2副、门神1副、红包1个,需付人民币22元,某人想印制16副对联、10副门神、22个红包共需付人民币______元.
6、重庆市举行了中学生足球联赛,共赛17轮(即每队均需比赛17场),记分办法是胜一场得3分,平一场得1分,负一场得0分.若文德中学足球队的积分为16分,且踢平场数是所负场数的整数倍,且胜、平、负的场数各不相同.则文德中学足球队共负____场.
7、已知式子,当时,其值为4;当时,其值为8;当时,其值为25;则当时,其值为__________.
8、坐落在北碚区北温泉境内的金刚碑古镇彰显了“一条石板路,千年金刚碑”鲜明的历史和地域特色,为了恢复古镇风貌,打造历史文化街区,政府开始对古镇进行保护性开发,现使用当地甲、乙、丙三种原料生产A、B两种工艺品进行销售.已知制作工艺品A每件需要甲原料1千克,乙原料1千克,丙原料4千克;制作工艺品B每件需要甲原料3千克,乙原料3千克,丙原料2千克.A、B两种工艺品的成本分别等于产品中所含的甲、乙、丙三种原料成本之和.已知每件工艺品B的成本是每千克丙原料成本的8倍,每件工艺品A的利润率是50%,每件工艺品B的利润率是25%,当A、B两种工艺品的销售件数之比是2:1时,求销售这两种工艺品的总销售利润率是_____.
三、解答题(共 6 小题)
1、在中,当x的值分别取1、-1、-2时,的值分别为1、9、19,求a、b、c的值.
2、解方程组:
(1);
(2).
3、已知多项式,当时,它的值是,当时,它的值是,试求的值.
4、阅读感悟:有些关于方程组的问题,欲求结果不是每一个未知数的值,而是关于未知数的代数式的值,如以下问题:
已知实数,满足①,②,求和的值.
本题常规的解题思路是将①,②两式联立组成方程组,解得,的值.再代入欲求值的代数式得到答案,常规思路运算量较大.其实,仔细观察两个方程未知数,的系数与所求代数式中,的系数之间的关系,本题还可以通过适当的变形整体求得代数式的值,由①-②得:,由①+②×2得.这样的解题思想就是通常所说的“整体思想”.
问题解决:
(1)已知二元一次方程组,则的值为______,的值为______.
(2)某班组织活动购买奖品,买5支铅笔、3块橡皮、2本日记本共需32元、买9支铅笔、5块橡皮、3本日记本共需58元,则购买3支铅笔、3块橡皮、3本日记本共需多少元?
(3)对于实数,,定义新运算:,其中,,是常数,等式右边是通常的加法和乘法运算.已知,,求的值.
5、解三元一次方程组:
6、一个手机号前三位数中,中间数字是前面数字的三倍;而第一个数字与第三个数字之和是中间数字的两倍.在后八位数中: 前四位数与后四位数之和是4461;前三位数与后五位数之和是82896.求这个手机号是?
