圆柱、圆锥的认识和圆柱的侧面积与表面积(讲义)-六年级下册数学苏教版(无答案)
文档属性
| 名称 | 圆柱、圆锥的认识和圆柱的侧面积与表面积(讲义)-六年级下册数学苏教版(无答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 676.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-23 00:00:00 | ||
图片预览




文档简介
学员姓名: 年 级:六年级 第 2 课时 学员学校: 辅导科目:数学 教师:申老师
课 题 圆柱、圆锥的认识和圆柱的侧面积与表面积
授课时间 2月26日 备课时间 2月23日
教学目标 熟练掌握圆柱的侧面积与表面积公式; 通过复习熟练掌握圆柱表面积与侧面积的相关应用; 通过讲解与练习,熟练掌握圆柱的表面积与侧面积的相关难题。
重点、难点 通过复习熟练掌握圆柱表面积与侧面积的相关应用; 通过讲解与练习,熟练掌握圆柱的表面积与侧面积的相关难题。
教学内容
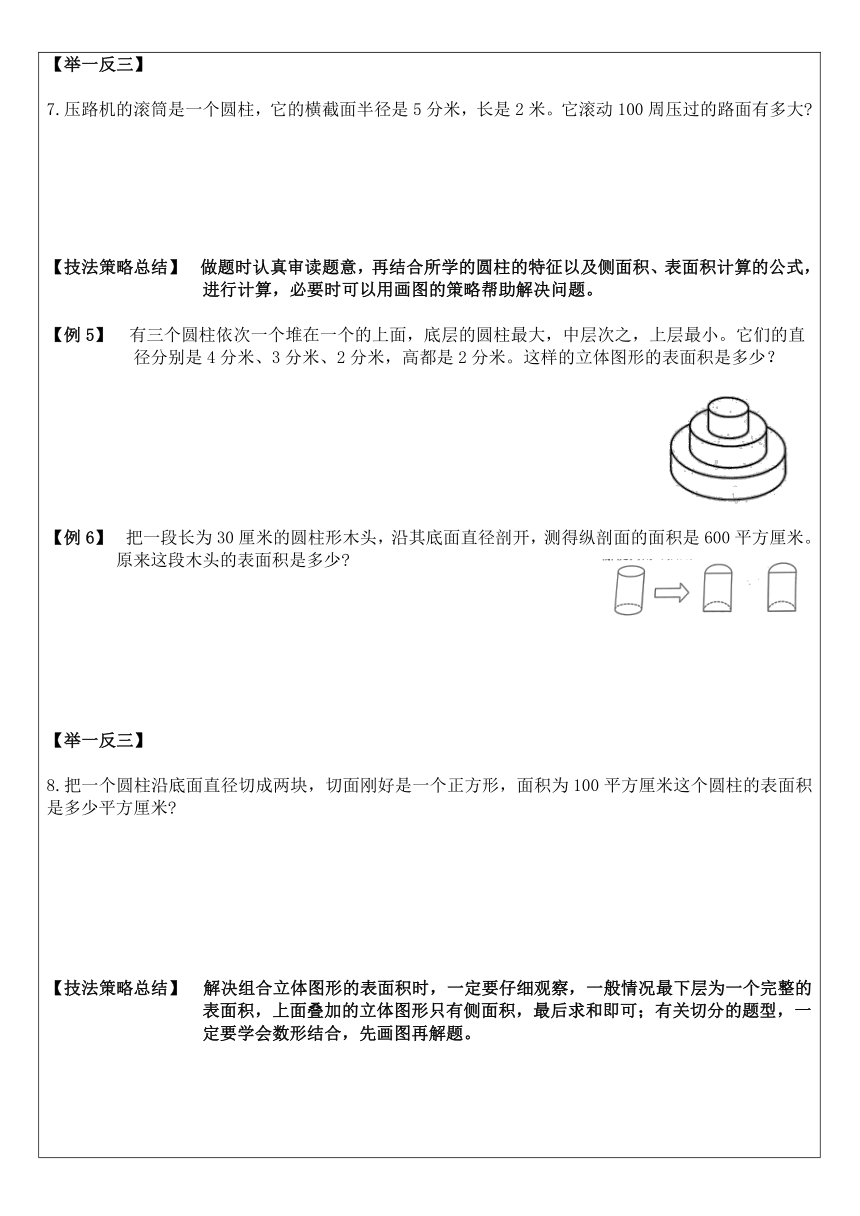
【课前练习】 一、填一填。 1.圆柱的上、下两个面叫作( ),它们是( )的两个( ),围成圆柱的曲面叫作( ),两个底面之间的( )叫作圆柱的高。 2.圆锥的底面是个( );圆锥的侧面是一个( )面;从圆锥顶点到底面圆心的距离是圆锥的( )。 3.把圆柱的侧面沿高展开得到一个( ),它的( )相当于圆柱的( ), ( )相当于圆柱的( )。 4.计算做一个圆柱形茶叶筒要多少铁皮,是要计算圆柱形的( )。 5.计算做一个圆柱形的烟肉要多少铁皮,是要计算圆柱形的( )。 6.一个圆柱的侧面积是1570平方厘米,高是5厘米,它的底面周长是( )厘米,底面积是( )平方厘米,表面积是( )平方厘米。 二、解决问题。 1.一个长方体的沙坑,长2米,宽1.5米,深0.3米。要在这个沙坑的四壁和底面涂上水泥,涂水泥的面积是多少平方米 2.把一个底面直径是6厘米、高是12厘米的圆柱体截成三段,表面积会增加多少平方厘米? 【知识点集锦】 1. 圆柱体简称“圆柱”,圆锥体简称“圆锥”。 2.圆柱的上、下两个面叫作底面, 围成圆柱的曲面叫作侧面, 两个底面之间的距离叫作高。 3.圆锥的底面是一个圆,侧面是一个曲面。 从圆锥的顶点到底面圆心的距离是圆锥的高。 当圆柱的(底面圆周长)和( 高 )相等时,侧面沿高展开图是正方形。 【经典例题讲解】 【例1】 一个圆柱的底面周长是25.12厘米,这个圆柱的一个底面面积是多少? 【举一反三】 1.一个圆柱的底面周长是50.24厘米,高是底面直径长度的2倍。这个圆柱的高是多少厘米 2.下面图形以竖线为轴旋转后会得到圆锥吗 如果会,说出圆锥的高和底面半径各是多少。 【技法策略总结】 做圆柱和圆锥的认识练习题时,要抓住圆柱有一个曲面、底面为圆形、有无数条 高的特征;要抓住圆锥有一个曲面、底面为圆形、高只有一条的特征。所以计算圆 柱或圆锥的底面积或周长时,利用圆的面积和周长公式计算即可。 【例2】 一个圆柱形铁皮烟,它的半径是2分米,高是8分米。如果把高增加到20分米,至少需要 增加多少平方分米的铁皮 【举一反三】 3.一个圆柱,如果把它的高截去2厘米,它的表面积就减少37.68平方厘米。这个圆柱的底面半径是多少厘米 4.一个圆柱的底面直径是3分米,把它的侧面展开正好是一个正方形。这个圆柱的高是多少分米 【技法策略总结】 计算圆柱的侧面积时,要紧紧抓住侧面的计算公式“侧面积=底面周长×高”,进 行灵活地计算。 【例3】 一个圆柱的底面周长是43.96厘米,表面积是659.4平方厘米。这个圆柱的高是多少厘米 【举一反三】 5.一个圆柱,若高减少4厘米,则表面积减少75.36平方厘米。求这个圆柱的底面积。 一个圆柱体的侧面积是50.24平方厘米,高和底面直径相等,这个圆柱体的表面积是多少 【技法策略总结】 圆柱的高增加或减少,它的表面积将会增加或减少高的那部分的侧面积,圆柱的 表面积公式经过推导变形,可知表面积是底面周长的(r+h)倍。 【例4】 有一张长方形铁皮(如图),剪下阴影部分恰好能制成圆柱体,求这个圆柱体的表面积。 【举一反三】 7.压路机的滚筒是一个圆柱,它的横截面半径是5分米,长是2米。它滚动100周压过的路面有多大 【技法策略总结】 做题时认真审读题意,再结合所学的圆柱的特征以及侧面积、表面积计算的公式, 进行计算,必要时可以用画图的策略帮助解决问题。 【例5】 有三个圆柱依次一个堆在一个的上面,底层的圆柱最大,中层次之,上层最小。它们的直 径分别是4分米、3分米、2分米,高都是2分米。这样的立体图形的表面积是多少? 【例6】 把一段长为30厘米的圆柱形木头,沿其底面直径剖开,测得纵剖面的面积是600平方厘米。 原来这段木头的表面积是多少 【举一反三】 8.把一个圆柱沿底面直径切成两块,切面刚好是一个正方形,面积为100平方厘米这个圆柱的表面积是多少平方厘米 【技法策略总结】 解决组合立体图形的表面积时,一定要仔细观察,一般情况最下层为一个完整的 表面积,上面叠加的立体图形只有侧面积,最后求和即可;有关切分的题型,一 定要学会数形结合,先画图再解题。 【课后作业】 1.把一个圆柱的侧面沿高展开得到一个边长为6.3厘米的正方形,它的侧面积是多少平方厘米 2.李师用铁皮加工做10节通风管,每节长1.2米,横截面直径为米一共要用铁皮多少平方米 (接口处忽略不计,得数用“进一”法保留整平方米) 3.广告公司制作了一个底面直径是1.5米、高是2.5米的圆柱形灯箱。它的侧面最多可以张贴多大面积的海报 4.一根圆柱形木料,锯下5分米的一段后,剩下木料的表面积减少了94.2平方分米。已知原圆柱体的底面直径和高相等,求原来的圆柱形木料的表面积。 5.压路机的滚简是圆柱体,它的长是2米,滚筒横截面的半径是0.6米。如果每分钟滚筒转动5周,那么每分钟可以压多大的路面 6.砌一个圆柱形水池,底面直径是6米,深2.5米。在池的底面和周围抹上水泥,抹水泥部分的面积是多少平方分米 7.把两个底面直径都是4厘米、长都是3分米圆柱形钢材焊接成一个大的圆柱形钢材。焊接成的圆柱形钢材的表面积比原来两个小圆柱形钢材的表面积之和减少了多少? 8.一块长为16.56分米、宽为8分米的长方形铁皮,现在要利用它制作一个圆柱形油桶。怎样制作浪费的铁皮最少 9.把一个圆柱沿底面直径切成两块,切面刚好是一个正方形,面积为64平方厘米这个圆柱的表面积是多少平方厘米 10.光华酒店大厅有8根同样的圆柱形柱子,每根高8米,底面直径是0.8米。把这些柱子漆成金黄色的,如果每平方米用油漆4.5千克,则一共需要油漆多少千克 (得数保留整数)
每日一练(周一)
一、填空题。
1.如下图,将一个直角三角形绕它较短的一条直角边旋转一周后所得的图形是( ),它的底面积是( )cm2。
2.把圆柱的底面分成若干个相等的扇形,切开后拼成一个近似的长方体。
(1)长方体的底面积等于圆柱的( ),长方体的高等于圆柱的( )。
(2)长方体的前、后两个面的面积之和,就是圆柱的( )。
(3)如果这个长方体的宽是2厘米、高是5厘米,那么圆柱的体积是( )立方厘米。
3.把一个底面半径为3厘米、高为10厘米的圆柱削成一个最大的圆锥,要削去( )立方厘米。
4.有一根长为2米的圆柱形钢材,如果把它截成3段圆柱形钢材,表面积比原来增加40平方厘米,这根圆柱形钢材的体积是( )立方厘米。
5.一个圆锥形冰淇淋的高是16厘米,底面半径是3厘米。如果每立方厘米重0.45克,这个冰淇淋重( )克。(结果保留整数)
6.一个圆柱和一个圆锥的底面积和体积分别相等,已知圆柱的高是6厘米,那么圆锥的高是( )厘米。
二、选择题。(把正确答案的序号填在括号里)
1.正方体、圆柱和圆锥的底面积相等,高也相等,下面说法正确的是( )。
A.圆柱的体积比正方体的体积小一些 B.圆锥的体积是正方体体积的
C.圆柱的体积与圆锥的体积相等 D.正方体的体积比圆柱的体积小一些
2.将一个底面直径为4厘米、高为5厘米的圆柱切成两部分,下面说法正确的是( )。
A.甲种切法增加的表面积大 B.乙种切法增加的表面积大
C.两种切法增加的表面积相等 D.无法判断
3.一个圆柱和一个圆锥的体积和底面积都相等,圆锥的高是3厘米,圆柱的高是( )厘米。
A.1 B.1.5 C.6 D.9
4.把一个圆柱形木块削去108立方厘米后,得到一个最大的圆锥,圆锥的体积是( )立方厘米。
A.54 B.108 C.216 D.270
三、求下面物体的体积。(单位: 厘米)
1. 2.
每日一练(周二)
一、判断题。(对的画“√”,错的画“ ”)
1.在一个圆锥形容器里装满沙土,然后倒入一个圆柱形容器,倒这样3次正好可以装满这个圆柱形容器。 ( )
2.求正方体、长方体、圆柱、圆锥的体积都可以用公式:体积=底面积×高。 ( )
3.一个圆锥与一个长方体等底等高,那么圆锥的体积等于长方体体积的。( )
4.圆锥的顶点到底面上任意一点的距离都是它的高。 ( )
5.一个圆柱的高扩大到原来的2倍,底面积缩小到原来的,它的体积不变。 ( )
二、解决问题。
1.一张DVD光盘的外直径是120mm,厚1.2mm,如果一个光盘盒能装50张这样的光盘,那么这个光盘盒的容积最少是多少立方厘米 (得数保留整数)
2.一节空心混凝土管道的内直径是60厘米,外直径是80厘米,长300厘米,浇制100节这种管道需要多少立方米的混凝土
3.压路机的滚筒是圆柱形的,如果滚筒的宽是2米,横截面半径是0.6米,那么滚筒转一周可压路多少平方米 如果压路机的滚筒每分钟转10周,那么10分钟可以压路多少米
每日一练(周三)
一、填空。
1.以一个长方形的长所在的直线为轴旋转一周,可以得到一个( ),长方形的长等于它的( ),长方形的宽等于它的( )。
2.一个圆柱的底面半径是2厘米,高是9厘米,它的侧面积是( )平方厘米,表面积是( )平方厘米,体积是( )立方厘米。
3.一个圆柱与一个圆锥等底等高,圆柱的体积比圆锥的体积大16立方分米,则圆柱的体积是( )立方分米,圆锥的体积是( )立方分米。
4.一个圆柱的侧面积是94.2平方厘米,底面半径是3厘米,圆柱的高是( )厘米。
5.一个圆锥形铁块的底面周长是12.56米,高是1.8米,它的体积是( )立方米。
6.一个圆柱的体积是78.5立方分米,底面积是15.7平方分米,与它等底等体积的圆锥的高是( )分米。
7.把一个底面半径是3厘米,长是2米的圆柱形木料截成两段,表面积增加了( )平方厘米。
二、图形计算。
1.求圆柱的表面积和体积。
2.求圆锥的体积。
每日一练(周四)
一、选择。
1.一个圆柱的侧面展开图不可能得到( )。
A.长方形 B.正方形 C.平行四边形 D.梯形
2.36个铁圆锥体,可以熔铸成( )个和它等底等高的圆柱体。
A.9 B.12 C.8
3.一个圆柱形钢管,内直径是20厘米,如果管内水的流速是4厘米/秒,这根水管1秒钟可以流出( )毫升水。
A.62.8 B.25.12 C.1256 D.12560
4.把一段圆柱形钢料削成一个最大的圆锥,削去部分重10千克,这段钢料重( )千克。
A.30 B.20 C.15 D.10
5.一个圆柱和一个圆锥的体积相等,它们的底面积之比是2∶1,则它们的高之比是( )。
A.1∶2 B.2∶1 C.1∶6
二、解决问题。
1.博物馆展览大厅有8根相同的圆柱,底面周长3.14米,高6米,要给这8根柱子刷上油漆,如果每平方米用油漆0.1千克,至少需要多少千克油漆?
2.一个圆锥形沙堆,底面周长6.28米,高1.2米,把这堆沙铺在一条宽10米的公路上,如果铺2厘米厚,能铺多长?
3.自来水管的内直径是2cm,管内水的流速是每秒20cm。一位同学打开水龙头洗手,走时忘了关,5分钟后被另一名同学发现才关上。大约浪费了多少升水
课 题 圆柱、圆锥的认识和圆柱的侧面积与表面积
授课时间 2月26日 备课时间 2月23日
教学目标 熟练掌握圆柱的侧面积与表面积公式; 通过复习熟练掌握圆柱表面积与侧面积的相关应用; 通过讲解与练习,熟练掌握圆柱的表面积与侧面积的相关难题。
重点、难点 通过复习熟练掌握圆柱表面积与侧面积的相关应用; 通过讲解与练习,熟练掌握圆柱的表面积与侧面积的相关难题。
教学内容
【课前练习】 一、填一填。 1.圆柱的上、下两个面叫作( ),它们是( )的两个( ),围成圆柱的曲面叫作( ),两个底面之间的( )叫作圆柱的高。 2.圆锥的底面是个( );圆锥的侧面是一个( )面;从圆锥顶点到底面圆心的距离是圆锥的( )。 3.把圆柱的侧面沿高展开得到一个( ),它的( )相当于圆柱的( ), ( )相当于圆柱的( )。 4.计算做一个圆柱形茶叶筒要多少铁皮,是要计算圆柱形的( )。 5.计算做一个圆柱形的烟肉要多少铁皮,是要计算圆柱形的( )。 6.一个圆柱的侧面积是1570平方厘米,高是5厘米,它的底面周长是( )厘米,底面积是( )平方厘米,表面积是( )平方厘米。 二、解决问题。 1.一个长方体的沙坑,长2米,宽1.5米,深0.3米。要在这个沙坑的四壁和底面涂上水泥,涂水泥的面积是多少平方米 2.把一个底面直径是6厘米、高是12厘米的圆柱体截成三段,表面积会增加多少平方厘米? 【知识点集锦】 1. 圆柱体简称“圆柱”,圆锥体简称“圆锥”。 2.圆柱的上、下两个面叫作底面, 围成圆柱的曲面叫作侧面, 两个底面之间的距离叫作高。 3.圆锥的底面是一个圆,侧面是一个曲面。 从圆锥的顶点到底面圆心的距离是圆锥的高。 当圆柱的(底面圆周长)和( 高 )相等时,侧面沿高展开图是正方形。 【经典例题讲解】 【例1】 一个圆柱的底面周长是25.12厘米,这个圆柱的一个底面面积是多少? 【举一反三】 1.一个圆柱的底面周长是50.24厘米,高是底面直径长度的2倍。这个圆柱的高是多少厘米 2.下面图形以竖线为轴旋转后会得到圆锥吗 如果会,说出圆锥的高和底面半径各是多少。 【技法策略总结】 做圆柱和圆锥的认识练习题时,要抓住圆柱有一个曲面、底面为圆形、有无数条 高的特征;要抓住圆锥有一个曲面、底面为圆形、高只有一条的特征。所以计算圆 柱或圆锥的底面积或周长时,利用圆的面积和周长公式计算即可。 【例2】 一个圆柱形铁皮烟,它的半径是2分米,高是8分米。如果把高增加到20分米,至少需要 增加多少平方分米的铁皮 【举一反三】 3.一个圆柱,如果把它的高截去2厘米,它的表面积就减少37.68平方厘米。这个圆柱的底面半径是多少厘米 4.一个圆柱的底面直径是3分米,把它的侧面展开正好是一个正方形。这个圆柱的高是多少分米 【技法策略总结】 计算圆柱的侧面积时,要紧紧抓住侧面的计算公式“侧面积=底面周长×高”,进 行灵活地计算。 【例3】 一个圆柱的底面周长是43.96厘米,表面积是659.4平方厘米。这个圆柱的高是多少厘米 【举一反三】 5.一个圆柱,若高减少4厘米,则表面积减少75.36平方厘米。求这个圆柱的底面积。 一个圆柱体的侧面积是50.24平方厘米,高和底面直径相等,这个圆柱体的表面积是多少 【技法策略总结】 圆柱的高增加或减少,它的表面积将会增加或减少高的那部分的侧面积,圆柱的 表面积公式经过推导变形,可知表面积是底面周长的(r+h)倍。 【例4】 有一张长方形铁皮(如图),剪下阴影部分恰好能制成圆柱体,求这个圆柱体的表面积。 【举一反三】 7.压路机的滚筒是一个圆柱,它的横截面半径是5分米,长是2米。它滚动100周压过的路面有多大 【技法策略总结】 做题时认真审读题意,再结合所学的圆柱的特征以及侧面积、表面积计算的公式, 进行计算,必要时可以用画图的策略帮助解决问题。 【例5】 有三个圆柱依次一个堆在一个的上面,底层的圆柱最大,中层次之,上层最小。它们的直 径分别是4分米、3分米、2分米,高都是2分米。这样的立体图形的表面积是多少? 【例6】 把一段长为30厘米的圆柱形木头,沿其底面直径剖开,测得纵剖面的面积是600平方厘米。 原来这段木头的表面积是多少 【举一反三】 8.把一个圆柱沿底面直径切成两块,切面刚好是一个正方形,面积为100平方厘米这个圆柱的表面积是多少平方厘米 【技法策略总结】 解决组合立体图形的表面积时,一定要仔细观察,一般情况最下层为一个完整的 表面积,上面叠加的立体图形只有侧面积,最后求和即可;有关切分的题型,一 定要学会数形结合,先画图再解题。 【课后作业】 1.把一个圆柱的侧面沿高展开得到一个边长为6.3厘米的正方形,它的侧面积是多少平方厘米 2.李师用铁皮加工做10节通风管,每节长1.2米,横截面直径为米一共要用铁皮多少平方米 (接口处忽略不计,得数用“进一”法保留整平方米) 3.广告公司制作了一个底面直径是1.5米、高是2.5米的圆柱形灯箱。它的侧面最多可以张贴多大面积的海报 4.一根圆柱形木料,锯下5分米的一段后,剩下木料的表面积减少了94.2平方分米。已知原圆柱体的底面直径和高相等,求原来的圆柱形木料的表面积。 5.压路机的滚简是圆柱体,它的长是2米,滚筒横截面的半径是0.6米。如果每分钟滚筒转动5周,那么每分钟可以压多大的路面 6.砌一个圆柱形水池,底面直径是6米,深2.5米。在池的底面和周围抹上水泥,抹水泥部分的面积是多少平方分米 7.把两个底面直径都是4厘米、长都是3分米圆柱形钢材焊接成一个大的圆柱形钢材。焊接成的圆柱形钢材的表面积比原来两个小圆柱形钢材的表面积之和减少了多少? 8.一块长为16.56分米、宽为8分米的长方形铁皮,现在要利用它制作一个圆柱形油桶。怎样制作浪费的铁皮最少 9.把一个圆柱沿底面直径切成两块,切面刚好是一个正方形,面积为64平方厘米这个圆柱的表面积是多少平方厘米 10.光华酒店大厅有8根同样的圆柱形柱子,每根高8米,底面直径是0.8米。把这些柱子漆成金黄色的,如果每平方米用油漆4.5千克,则一共需要油漆多少千克 (得数保留整数)
每日一练(周一)
一、填空题。
1.如下图,将一个直角三角形绕它较短的一条直角边旋转一周后所得的图形是( ),它的底面积是( )cm2。
2.把圆柱的底面分成若干个相等的扇形,切开后拼成一个近似的长方体。
(1)长方体的底面积等于圆柱的( ),长方体的高等于圆柱的( )。
(2)长方体的前、后两个面的面积之和,就是圆柱的( )。
(3)如果这个长方体的宽是2厘米、高是5厘米,那么圆柱的体积是( )立方厘米。
3.把一个底面半径为3厘米、高为10厘米的圆柱削成一个最大的圆锥,要削去( )立方厘米。
4.有一根长为2米的圆柱形钢材,如果把它截成3段圆柱形钢材,表面积比原来增加40平方厘米,这根圆柱形钢材的体积是( )立方厘米。
5.一个圆锥形冰淇淋的高是16厘米,底面半径是3厘米。如果每立方厘米重0.45克,这个冰淇淋重( )克。(结果保留整数)
6.一个圆柱和一个圆锥的底面积和体积分别相等,已知圆柱的高是6厘米,那么圆锥的高是( )厘米。
二、选择题。(把正确答案的序号填在括号里)
1.正方体、圆柱和圆锥的底面积相等,高也相等,下面说法正确的是( )。
A.圆柱的体积比正方体的体积小一些 B.圆锥的体积是正方体体积的
C.圆柱的体积与圆锥的体积相等 D.正方体的体积比圆柱的体积小一些
2.将一个底面直径为4厘米、高为5厘米的圆柱切成两部分,下面说法正确的是( )。
A.甲种切法增加的表面积大 B.乙种切法增加的表面积大
C.两种切法增加的表面积相等 D.无法判断
3.一个圆柱和一个圆锥的体积和底面积都相等,圆锥的高是3厘米,圆柱的高是( )厘米。
A.1 B.1.5 C.6 D.9
4.把一个圆柱形木块削去108立方厘米后,得到一个最大的圆锥,圆锥的体积是( )立方厘米。
A.54 B.108 C.216 D.270
三、求下面物体的体积。(单位: 厘米)
1. 2.
每日一练(周二)
一、判断题。(对的画“√”,错的画“ ”)
1.在一个圆锥形容器里装满沙土,然后倒入一个圆柱形容器,倒这样3次正好可以装满这个圆柱形容器。 ( )
2.求正方体、长方体、圆柱、圆锥的体积都可以用公式:体积=底面积×高。 ( )
3.一个圆锥与一个长方体等底等高,那么圆锥的体积等于长方体体积的。( )
4.圆锥的顶点到底面上任意一点的距离都是它的高。 ( )
5.一个圆柱的高扩大到原来的2倍,底面积缩小到原来的,它的体积不变。 ( )
二、解决问题。
1.一张DVD光盘的外直径是120mm,厚1.2mm,如果一个光盘盒能装50张这样的光盘,那么这个光盘盒的容积最少是多少立方厘米 (得数保留整数)
2.一节空心混凝土管道的内直径是60厘米,外直径是80厘米,长300厘米,浇制100节这种管道需要多少立方米的混凝土
3.压路机的滚筒是圆柱形的,如果滚筒的宽是2米,横截面半径是0.6米,那么滚筒转一周可压路多少平方米 如果压路机的滚筒每分钟转10周,那么10分钟可以压路多少米
每日一练(周三)
一、填空。
1.以一个长方形的长所在的直线为轴旋转一周,可以得到一个( ),长方形的长等于它的( ),长方形的宽等于它的( )。
2.一个圆柱的底面半径是2厘米,高是9厘米,它的侧面积是( )平方厘米,表面积是( )平方厘米,体积是( )立方厘米。
3.一个圆柱与一个圆锥等底等高,圆柱的体积比圆锥的体积大16立方分米,则圆柱的体积是( )立方分米,圆锥的体积是( )立方分米。
4.一个圆柱的侧面积是94.2平方厘米,底面半径是3厘米,圆柱的高是( )厘米。
5.一个圆锥形铁块的底面周长是12.56米,高是1.8米,它的体积是( )立方米。
6.一个圆柱的体积是78.5立方分米,底面积是15.7平方分米,与它等底等体积的圆锥的高是( )分米。
7.把一个底面半径是3厘米,长是2米的圆柱形木料截成两段,表面积增加了( )平方厘米。
二、图形计算。
1.求圆柱的表面积和体积。
2.求圆锥的体积。
每日一练(周四)
一、选择。
1.一个圆柱的侧面展开图不可能得到( )。
A.长方形 B.正方形 C.平行四边形 D.梯形
2.36个铁圆锥体,可以熔铸成( )个和它等底等高的圆柱体。
A.9 B.12 C.8
3.一个圆柱形钢管,内直径是20厘米,如果管内水的流速是4厘米/秒,这根水管1秒钟可以流出( )毫升水。
A.62.8 B.25.12 C.1256 D.12560
4.把一段圆柱形钢料削成一个最大的圆锥,削去部分重10千克,这段钢料重( )千克。
A.30 B.20 C.15 D.10
5.一个圆柱和一个圆锥的体积相等,它们的底面积之比是2∶1,则它们的高之比是( )。
A.1∶2 B.2∶1 C.1∶6
二、解决问题。
1.博物馆展览大厅有8根相同的圆柱,底面周长3.14米,高6米,要给这8根柱子刷上油漆,如果每平方米用油漆0.1千克,至少需要多少千克油漆?
2.一个圆锥形沙堆,底面周长6.28米,高1.2米,把这堆沙铺在一条宽10米的公路上,如果铺2厘米厚,能铺多长?
3.自来水管的内直径是2cm,管内水的流速是每秒20cm。一位同学打开水龙头洗手,走时忘了关,5分钟后被另一名同学发现才关上。大约浪费了多少升水
