【解析版】福建省福州市2014届高三质检数学理试题
文档属性
| 名称 | 【解析版】福建省福州市2014届高三质检数学理试题 |

|
|
| 格式 | zip | ||
| 文件大小 | 569.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-04-01 00:00:00 | ||
图片预览



文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
2014年福州市高中毕业班质量检测
理科数学试卷
第Ⅰ卷(选择题 共50分)
一、选择题:本大题共10小题.每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知集合,若,则是实数的取值范围是( )
A. B. C. D.
2.“实数”是“复数(为虚数单位)的模为”的 ( )
A.充分非必要条件 B.必要非充分条件 C.充要条件 D.既不是充分条件又不是必要条件
3.执行如图所示的程序框图,输出的值是 ( )
A.2 B. C. D.
【答案】B
4.命题“,使得”的否定是 ( )
A. ,都有 B.不存在,使
C. 都有 D. 使
5.已知等比数列的前项积记为,若,则 ( )
A.512 B.256 C.81 D.16
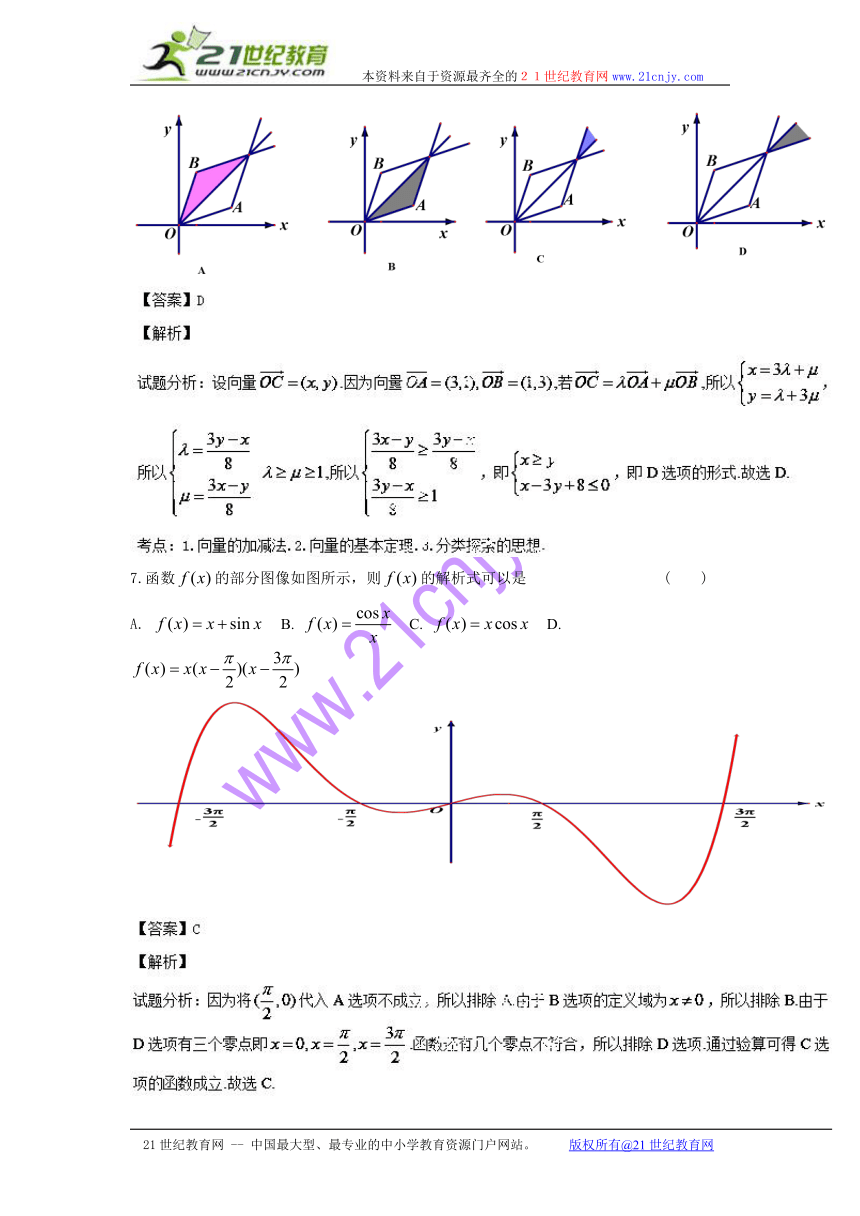
6.如图,设向量,若,且,则用阴影表示点所有可能的位置区域正确的是 ( )
7.函数的部分图像如图所示,则的解析式可以是 ( )
A. B. C. D.
考点:1.函数的图像.2.分类讨论.3.列举排除的数学思想.4.归纳化归的数学思想.
8.已知、是双曲线的左、右焦点,若双曲线左支上存在一点一点与点关于直线对称,则该双曲线的离心率为 ( )
A. B. C. D.
9.若定义在R上的函数f(x)满足f(-x)=f(x), f(2-x)=f(x),且当x∈[0,1]时,其图象是四分
之一圆(如图所示),则函数H(x)= |xex|-f(x)在区间[-3,1]上的零点个数为 ( )
A.5 B.4 C.3 D.2
【答案】B
【解析】
试题分析:因为定义在R上的函数f(x)满足f(-x)=f(x),所以函数为偶函数,又因为f(2-x)=f(x),所以函数关于直线对称.因为函数H(x)= |xex|-f(x)在区间[-3,1]上的零点即等价求方程的解的个数.等价于函数和函数的图像的交点个数,由图象可得共有4个交点.故选B.
考点:1.函数的性质.2.数形结合的思想.3.函数图像的正确表示及绘制.
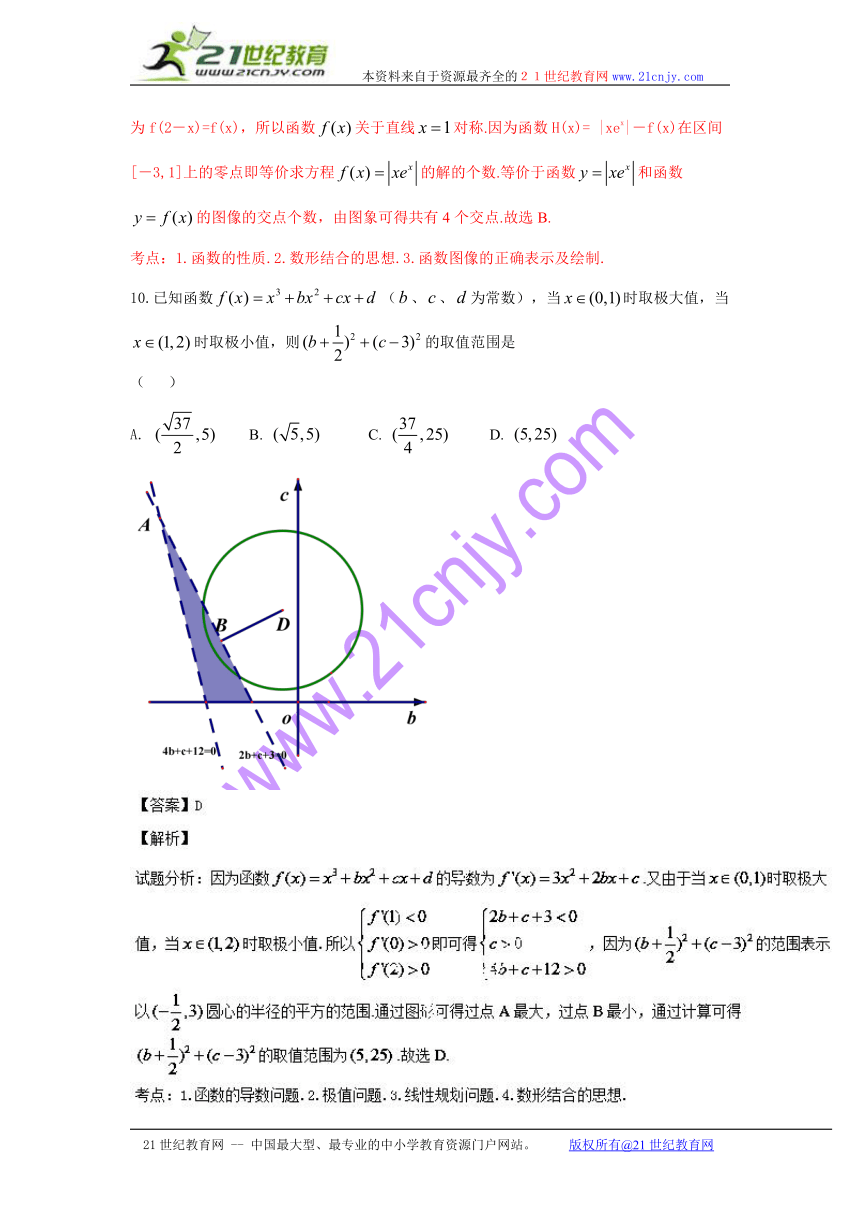
10.已知函数(、、为常数),当时取极大值,当时取极小值,则的取值范围是 ( )
A. B. C. D.
第Ⅱ卷(共100分)
二、填空题:本大题共5小题,每小题4分,共20分.
11.5名同学站成一排,其中甲同学不站排头,则不同的排法种数是______________(用数字作答).
12.如图所示,在边长为1的正方形中任取一点,则点恰好取自阴影部分的概率为________.
14.已知某几何体的三视图(单位:cm)如图所示,则该几何体的表面积为____________.
15.已知函数,若数列满足,且的前项和为,则_____________.
【答案】8042
【解析】
试题分析:.因为,,,,,,,.所以8042.
考点:1.分段函数的问题.2.数列的思想.3.三角函数的周期性.4.分类列举的数学思想.
三、解答题 (本大题共6小题,共80分.解答应写出文字说明、证明过程或演算步骤.)
16.(本小题满分13分)在对某渔业产品的质量调研中,从甲、乙两地出产的该产品中各随机抽取10件,测量该产品中某种元素的含量(单位:毫克).下表是测量数据的茎叶图:
规定:当产品中的此种元素含量毫克时为优质品.
(Ⅰ)试用上述样本数据估计甲、乙两地该产品的优质品率(优质品件数/总件数);
(Ⅱ)从乙地抽出的上述10件产品中,随机抽取3件,求抽到的3件产品中优质品数的分布列及数学期望.
(II)的取值为1,2,3.
所以的分布列为
1 2 3
故的数学期望为
考点:1.茎叶图的知识.2.列举对比的数学思想.3.数学期望的计算.4.概率知识.
17.(本小题满分13分)已知函数.
(Ⅰ)当时,求函数的单调递增区间;
(Ⅱ)设的内角的对应边分别为,且若向量与向量共线,求的值.
令,
18.(本小题满分13分) 如图,直角梯形中,,点分别是的中点,点在上,沿将梯形翻折,使平面平面.
(Ⅰ)当最小时,求证:;
(Ⅱ)当时,求二面角平面角的余弦值.
【答案】(Ⅰ)参考解析;(Ⅱ)
【解析】
试题分析:(Ⅰ)因为当最小时,及连结AC与EF的交点即为G点,通过三角形的相似可得到EG的长度.需要证明直线与直线垂直,根据题意建立空间直角坐标系,即可得到相关各点的坐标,从而写出相
(Ⅱ)解法一:设EG=k,
∥平面,点D到平面EFCB的距离为即为点A到平面EFCB的距离.
[(3- k)+4]2=7-k
=
又=,
,=,
即EG=1
设平面DBG的法向量为,∵G(0,1,0),
∴(-2,2,2),
则 ,即
19.(本小题满分13分) 已知动圆过定点(1,0),且与直线相切.
(Ⅰ)求动圆圆心的轨迹方程;
(Ⅱ)设是轨迹上异于原点的两个不同点,直线和的倾斜角分别为和,①当时,求证直线恒过一定点;
②若为定值,直线是否仍恒过一定点,若存在,试求出定点的坐标;若不存在,请说明理由.
20.(本小题满分14分) 已知函数,其中且
(Ⅰ)讨论的单调区间;
(Ⅱ)若直线的图像恒在函数图像的上方,求的取值范围;
(Ⅲ)若存在,使得,求证:.
【答案】(Ⅰ)参考解析;(Ⅱ);(Ⅲ)参考解析
【解析】
的最小值为,所以只需
即,,
(Ⅲ)由于当时函数在上是增函数,不满足题意,所以
21.本小题设有(1)、(2)、(3)三个选考题,每题7分,请考生任选2题作答,满分14分.如果多做,则安所做的前两题计分.作答时,先用2B铅笔在答题卡上把所选题目对应提好右边的方框涂黑,并将所选题号填入括号中.
(1)(本小题满分7分)选修4-2:矩阵与变换.
已知矩阵 ,若矩阵属于特征值6的一个特征向量为,属于特征值1的一个特征向量.
(Ⅰ)求矩阵的逆矩阵;
(Ⅱ)计算
【答案】(Ⅰ);(Ⅱ)
【解析】
试题分析:(Ⅰ)因为已知矩阵 ,若矩阵属于特征值6的一个特征向量为,属于特征值1的一个特征向量.通过特征向量与特征值的关系,可求矩阵A中的相应参数的值,再通过逆矩阵的含义可求出矩阵A的逆矩阵.同样可以从通过特征根的方程方面入手,求的结论.
(2)(本小题满分7分)选修4-4:坐标与参数方程.
在平面直角坐标系中,以为极点,轴非负半轴为极轴建立坐标系,已知曲线的极坐标方程为,直线的参数方程为: (为参数),两曲线相交于两点.
(Ⅰ)写出曲线的直角坐标方程和直线的普通方程;
(Ⅱ)若求的值.
(3)(本小题满分7分)选修4-5:不等式选讲
设函数,
(Ⅰ)求的最小值;
(Ⅱ)当时,求的最小值.
【答案】(Ⅰ)1;(Ⅱ)
【解析】
试题分析:(Ⅰ)因为,所以通过绝对值的基本不等式,即可得到最小值.另外也可以通过分类关键是去绝对值,求出不同类的函数式的最小值,再根据这些最小值中的最小值确定所求的结论.
开始
M=2
i=1
i<5
i=i+1
输出M
结束
否
是
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
2014年福州市高中毕业班质量检测
理科数学试卷
第Ⅰ卷(选择题 共50分)
一、选择题:本大题共10小题.每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知集合,若,则是实数的取值范围是( )
A. B. C. D.
2.“实数”是“复数(为虚数单位)的模为”的 ( )
A.充分非必要条件 B.必要非充分条件 C.充要条件 D.既不是充分条件又不是必要条件
3.执行如图所示的程序框图,输出的值是 ( )
A.2 B. C. D.
【答案】B
4.命题“,使得”的否定是 ( )
A. ,都有 B.不存在,使
C. 都有 D. 使
5.已知等比数列的前项积记为,若,则 ( )
A.512 B.256 C.81 D.16
6.如图,设向量,若,且,则用阴影表示点所有可能的位置区域正确的是 ( )
7.函数的部分图像如图所示,则的解析式可以是 ( )
A. B. C. D.
考点:1.函数的图像.2.分类讨论.3.列举排除的数学思想.4.归纳化归的数学思想.
8.已知、是双曲线的左、右焦点,若双曲线左支上存在一点一点与点关于直线对称,则该双曲线的离心率为 ( )
A. B. C. D.
9.若定义在R上的函数f(x)满足f(-x)=f(x), f(2-x)=f(x),且当x∈[0,1]时,其图象是四分
之一圆(如图所示),则函数H(x)= |xex|-f(x)在区间[-3,1]上的零点个数为 ( )
A.5 B.4 C.3 D.2
【答案】B
【解析】
试题分析:因为定义在R上的函数f(x)满足f(-x)=f(x),所以函数为偶函数,又因为f(2-x)=f(x),所以函数关于直线对称.因为函数H(x)= |xex|-f(x)在区间[-3,1]上的零点即等价求方程的解的个数.等价于函数和函数的图像的交点个数,由图象可得共有4个交点.故选B.
考点:1.函数的性质.2.数形结合的思想.3.函数图像的正确表示及绘制.
10.已知函数(、、为常数),当时取极大值,当时取极小值,则的取值范围是 ( )
A. B. C. D.
第Ⅱ卷(共100分)
二、填空题:本大题共5小题,每小题4分,共20分.
11.5名同学站成一排,其中甲同学不站排头,则不同的排法种数是______________(用数字作答).
12.如图所示,在边长为1的正方形中任取一点,则点恰好取自阴影部分的概率为________.
14.已知某几何体的三视图(单位:cm)如图所示,则该几何体的表面积为____________.
15.已知函数,若数列满足,且的前项和为,则_____________.
【答案】8042
【解析】
试题分析:.因为,,,,,,,.所以8042.
考点:1.分段函数的问题.2.数列的思想.3.三角函数的周期性.4.分类列举的数学思想.
三、解答题 (本大题共6小题,共80分.解答应写出文字说明、证明过程或演算步骤.)
16.(本小题满分13分)在对某渔业产品的质量调研中,从甲、乙两地出产的该产品中各随机抽取10件,测量该产品中某种元素的含量(单位:毫克).下表是测量数据的茎叶图:
规定:当产品中的此种元素含量毫克时为优质品.
(Ⅰ)试用上述样本数据估计甲、乙两地该产品的优质品率(优质品件数/总件数);
(Ⅱ)从乙地抽出的上述10件产品中,随机抽取3件,求抽到的3件产品中优质品数的分布列及数学期望.
(II)的取值为1,2,3.
所以的分布列为
1 2 3
故的数学期望为
考点:1.茎叶图的知识.2.列举对比的数学思想.3.数学期望的计算.4.概率知识.
17.(本小题满分13分)已知函数.
(Ⅰ)当时,求函数的单调递增区间;
(Ⅱ)设的内角的对应边分别为,且若向量与向量共线,求的值.
令,
18.(本小题满分13分) 如图,直角梯形中,,点分别是的中点,点在上,沿将梯形翻折,使平面平面.
(Ⅰ)当最小时,求证:;
(Ⅱ)当时,求二面角平面角的余弦值.
【答案】(Ⅰ)参考解析;(Ⅱ)
【解析】
试题分析:(Ⅰ)因为当最小时,及连结AC与EF的交点即为G点,通过三角形的相似可得到EG的长度.需要证明直线与直线垂直,根据题意建立空间直角坐标系,即可得到相关各点的坐标,从而写出相
(Ⅱ)解法一:设EG=k,
∥平面,点D到平面EFCB的距离为即为点A到平面EFCB的距离.
[(3- k)+4]2=7-k
=
又=,
,=,
即EG=1
设平面DBG的法向量为,∵G(0,1,0),
∴(-2,2,2),
则 ,即
19.(本小题满分13分) 已知动圆过定点(1,0),且与直线相切.
(Ⅰ)求动圆圆心的轨迹方程;
(Ⅱ)设是轨迹上异于原点的两个不同点,直线和的倾斜角分别为和,①当时,求证直线恒过一定点;
②若为定值,直线是否仍恒过一定点,若存在,试求出定点的坐标;若不存在,请说明理由.
20.(本小题满分14分) 已知函数,其中且
(Ⅰ)讨论的单调区间;
(Ⅱ)若直线的图像恒在函数图像的上方,求的取值范围;
(Ⅲ)若存在,使得,求证:.
【答案】(Ⅰ)参考解析;(Ⅱ);(Ⅲ)参考解析
【解析】
的最小值为,所以只需
即,,
(Ⅲ)由于当时函数在上是增函数,不满足题意,所以
21.本小题设有(1)、(2)、(3)三个选考题,每题7分,请考生任选2题作答,满分14分.如果多做,则安所做的前两题计分.作答时,先用2B铅笔在答题卡上把所选题目对应提好右边的方框涂黑,并将所选题号填入括号中.
(1)(本小题满分7分)选修4-2:矩阵与变换.
已知矩阵 ,若矩阵属于特征值6的一个特征向量为,属于特征值1的一个特征向量.
(Ⅰ)求矩阵的逆矩阵;
(Ⅱ)计算
【答案】(Ⅰ);(Ⅱ)
【解析】
试题分析:(Ⅰ)因为已知矩阵 ,若矩阵属于特征值6的一个特征向量为,属于特征值1的一个特征向量.通过特征向量与特征值的关系,可求矩阵A中的相应参数的值,再通过逆矩阵的含义可求出矩阵A的逆矩阵.同样可以从通过特征根的方程方面入手,求的结论.
(2)(本小题满分7分)选修4-4:坐标与参数方程.
在平面直角坐标系中,以为极点,轴非负半轴为极轴建立坐标系,已知曲线的极坐标方程为,直线的参数方程为: (为参数),两曲线相交于两点.
(Ⅰ)写出曲线的直角坐标方程和直线的普通方程;
(Ⅱ)若求的值.
(3)(本小题满分7分)选修4-5:不等式选讲
设函数,
(Ⅰ)求的最小值;
(Ⅱ)当时,求的最小值.
【答案】(Ⅰ)1;(Ⅱ)
【解析】
试题分析:(Ⅰ)因为,所以通过绝对值的基本不等式,即可得到最小值.另外也可以通过分类关键是去绝对值,求出不同类的函数式的最小值,再根据这些最小值中的最小值确定所求的结论.
开始
M=2
i=1
i<5
i=i+1
输出M
结束
否
是
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
同课章节目录
