华师版七年级数学下册第7章 二元一次方程组 复习与小结 原创新授课件(共13张PPT)
文档属性
| 名称 | 华师版七年级数学下册第7章 二元一次方程组 复习与小结 原创新授课件(共13张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-24 00:00:00 | ||
图片预览





文档简介
(共13张PPT)
第七章 一次方程组
第7章复习与小结
一、学习目标
重点
难点
二、学习重难点
1.对二元一次方程(组),二元一次方程以及二元一次方程组的解有进一步理解,能熟练准确地用代入法和加减法解二元一次方程组.
2.能较熟练地列出一次方程组解简单的应用题.
解二元一次方程组以及列方程组解应用题.
找出等量关系列出二元一次方程组.
活动1 旧知回顾
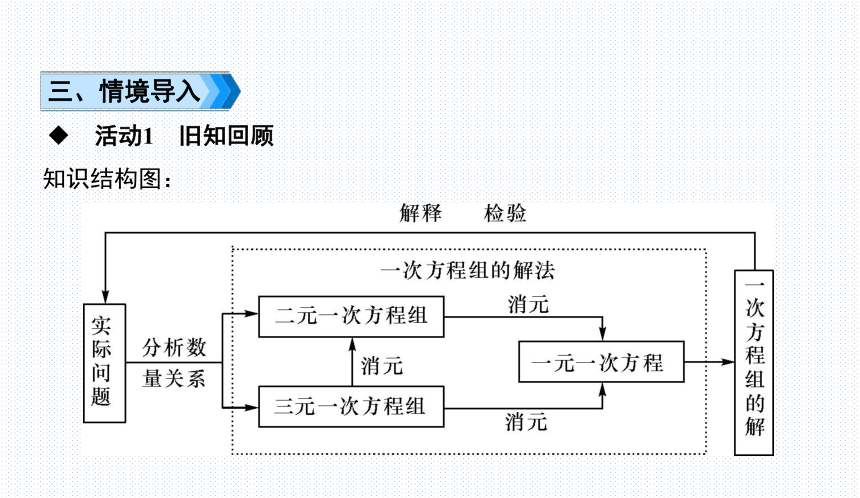
三、情境导入
知识结构图:
活动1 自主探究1
四、自学互研
1.二元一次方程的概念:
含有两个未知数,且未知数的次数是1的等式.
2.二元一次方程组:
两个二元一次方程合在一起.
3.二元一次方程组的解:
使二元一次方程组中两个方程的左右两边都相等的两个未知数的值.
4.解二元一次方程组的思想:
消元,转化.解法:代入法和加减法.
活动2 合作探究1
例1:二元一次方程3x+y=10在正整数范围内解的组数是( )
A.1 B.2 C.3 D.4
分析:观察系数,可以从y入手,y=10-3x,x可取1,2,3.
例2:已知 是二元一次方程组 的解,则b-a的值为( )
A.0 B.1 C.2 D.3
分析:将x、y的值代入方程组求出a、b的值即可.
C
A
例3:如果三元一次方程组 的解也是方程ax+3y-z=6的解,则a的值为( )
A.1 B.2 C.3 D.4
分析:观察三个未知数的系数,都为1,所以可以将三个方程左右两边加起来,得x+y+z=6,用这个等式依次减去三个方程可得解,再代入方程即可求出a的值.
C
例4:解方程组:(1) (2)
解:(1) (2)
活动3 自主探究2
1.在实际问题中,常会遇到有多个未知量的问题,二元一次方程组是反映现实世界数量之间相等关系的数学模型之一,将实际问题转化为二元一次方程组.
2.通过列方程组来解某些实际问题,应注意检验和正确作答,检验不仅要检查求得的解是否适合方程组的每一个方程,更重要的是要考察所得的解答是否符合实际问题的要求.
活动4 合作探究2
例5:A、B两地相距150 km,甲、乙两车分别从A、B两地同时出发,同向而行,甲车3 h可追上乙车;相向而行,两车1.5 h相遇,求甲、乙两车的速度.
解得
解:设甲车的速度为x km/h,乙车的速度为y km/h,
答:甲、乙两车的速度分别是75 km/h,25 km/h.
根据题意,得
例6:两块试验田去年共产花生470 kg,改用良种后,今年共产花生523 kg.已知其中第一块田的产量比去年增产16%,第二块田的产量比去年增产10%.这两块田改用良种前每块田产量分别是多少千克?今年每块田各增产多少千克?
解:设去年第一块田花生产量为x kg,第二块田花生产量为y kg,
则
∴今年第一块田增产100×16%=16(kg),第二块田增产370×10%=37(kg).
解得
答:这两块田改用良种前每块田产量分别是100 kg、370 kg,今年每块田各增产16 kg、37 kg.
活动5
完成
《名师测控》手册
《精英新课堂》手册
活动6 课堂小结
一次方程与方程组
概念与性质
应用
一元一次方程
等式的性质
二元一次方程
一元一次方程组
一元一次方程组
方程的解
性质1
性质2
性质3
性质4
解方程
方程(组)的解
二元一次方程组
一元一次方程
实际问题
方程(组)
消元
代入法
加减法
五、作业布置与教学反思
1.作业布置
课时练习.
2.教学反思
第七章 一次方程组
第7章复习与小结
一、学习目标
重点
难点
二、学习重难点
1.对二元一次方程(组),二元一次方程以及二元一次方程组的解有进一步理解,能熟练准确地用代入法和加减法解二元一次方程组.
2.能较熟练地列出一次方程组解简单的应用题.
解二元一次方程组以及列方程组解应用题.
找出等量关系列出二元一次方程组.
活动1 旧知回顾
三、情境导入
知识结构图:
活动1 自主探究1
四、自学互研
1.二元一次方程的概念:
含有两个未知数,且未知数的次数是1的等式.
2.二元一次方程组:
两个二元一次方程合在一起.
3.二元一次方程组的解:
使二元一次方程组中两个方程的左右两边都相等的两个未知数的值.
4.解二元一次方程组的思想:
消元,转化.解法:代入法和加减法.
活动2 合作探究1
例1:二元一次方程3x+y=10在正整数范围内解的组数是( )
A.1 B.2 C.3 D.4
分析:观察系数,可以从y入手,y=10-3x,x可取1,2,3.
例2:已知 是二元一次方程组 的解,则b-a的值为( )
A.0 B.1 C.2 D.3
分析:将x、y的值代入方程组求出a、b的值即可.
C
A
例3:如果三元一次方程组 的解也是方程ax+3y-z=6的解,则a的值为( )
A.1 B.2 C.3 D.4
分析:观察三个未知数的系数,都为1,所以可以将三个方程左右两边加起来,得x+y+z=6,用这个等式依次减去三个方程可得解,再代入方程即可求出a的值.
C
例4:解方程组:(1) (2)
解:(1) (2)
活动3 自主探究2
1.在实际问题中,常会遇到有多个未知量的问题,二元一次方程组是反映现实世界数量之间相等关系的数学模型之一,将实际问题转化为二元一次方程组.
2.通过列方程组来解某些实际问题,应注意检验和正确作答,检验不仅要检查求得的解是否适合方程组的每一个方程,更重要的是要考察所得的解答是否符合实际问题的要求.
活动4 合作探究2
例5:A、B两地相距150 km,甲、乙两车分别从A、B两地同时出发,同向而行,甲车3 h可追上乙车;相向而行,两车1.5 h相遇,求甲、乙两车的速度.
解得
解:设甲车的速度为x km/h,乙车的速度为y km/h,
答:甲、乙两车的速度分别是75 km/h,25 km/h.
根据题意,得
例6:两块试验田去年共产花生470 kg,改用良种后,今年共产花生523 kg.已知其中第一块田的产量比去年增产16%,第二块田的产量比去年增产10%.这两块田改用良种前每块田产量分别是多少千克?今年每块田各增产多少千克?
解:设去年第一块田花生产量为x kg,第二块田花生产量为y kg,
则
∴今年第一块田增产100×16%=16(kg),第二块田增产370×10%=37(kg).
解得
答:这两块田改用良种前每块田产量分别是100 kg、370 kg,今年每块田各增产16 kg、37 kg.
活动5
完成
《名师测控》手册
《精英新课堂》手册
活动6 课堂小结
一次方程与方程组
概念与性质
应用
一元一次方程
等式的性质
二元一次方程
一元一次方程组
一元一次方程组
方程的解
性质1
性质2
性质3
性质4
解方程
方程(组)的解
二元一次方程组
一元一次方程
实际问题
方程(组)
消元
代入法
加减法
五、作业布置与教学反思
1.作业布置
课时练习.
2.教学反思
