8.5 空间直线、平面的平行——2022-2023学年高一数学人教A版(2019)必修第二册课时同步练习(含解析)
文档属性
| 名称 | 8.5 空间直线、平面的平行——2022-2023学年高一数学人教A版(2019)必修第二册课时同步练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 901.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-23 17:00:37 | ||
图片预览



文档简介
8.5 空间直线、平面的平行
【教材课后习题】
1.选择题
(1)若直线a不平行于平面,则下列结论成立的是( ).
A.内的所有直线都与a异面 B.内不存在与a平行的直线
C.内的直线都与a相交 D.直线a与平面有公共点
(2)如果直线平面,,那么过点P且平行于直线a的直线( ).
A.只有一条,不在平面内 B.有无数条,不一定在内
C.只有一条,且在平面内 D.有无数条,一定在内
2.已知平面和直线a,b,c,且,,,,则与的位置关系是_________.
3.如图,在长方体木块中,面上有一点P,怎样过点P画一条直线与棱CD平行
4.如图,在长方体中,E,F分别是AB,BC的中点,求证.
5.如图,在四面体中,E,F,G分别是AB,BC,CD的中点,求证:
(1)平面EFG;
(2)平面EFG.
6.如图,a,b是异面直线,画出平面,使,且,并说明理由.
7.如图,,,,,求证.
8.如图,直线,,相交于点O,,,求证:平面平面.
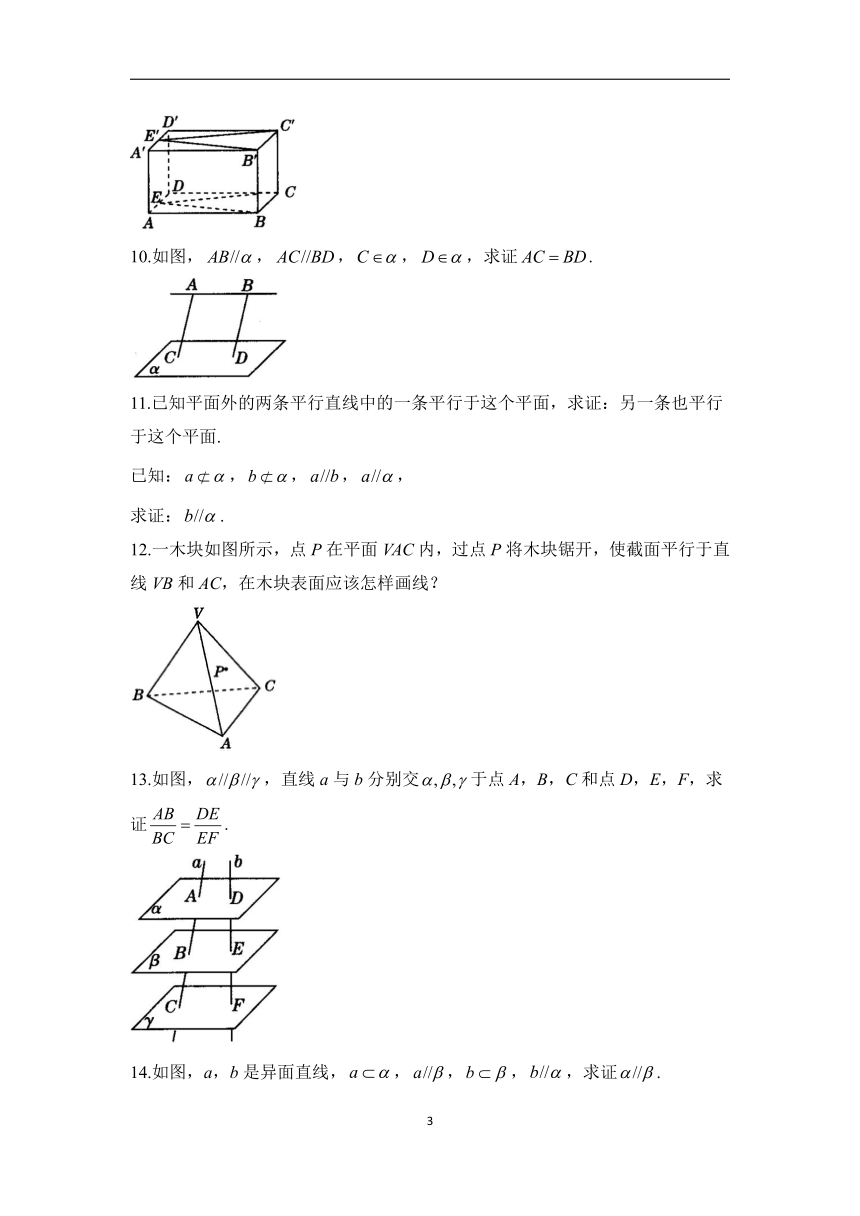
9.如图,E,分别为长方体的棱AD,的中点,求证.
10.如图,,,,,求证.
11.已知平面外的两条平行直线中的一条平行于这个平面,求证:另一条也平行于这个平面.
已知:,,,,
求证:.
12.一木块如图所示,点P在平面VAC内,过点P将木块锯开,使截面平行于直线VB和AC,在木块表面应该怎样画线?
13.如图,,直线a与b分别交于点A,B,C和点D,E,F,求证.
14.如图,a,b是异面直线,,,,,求证.
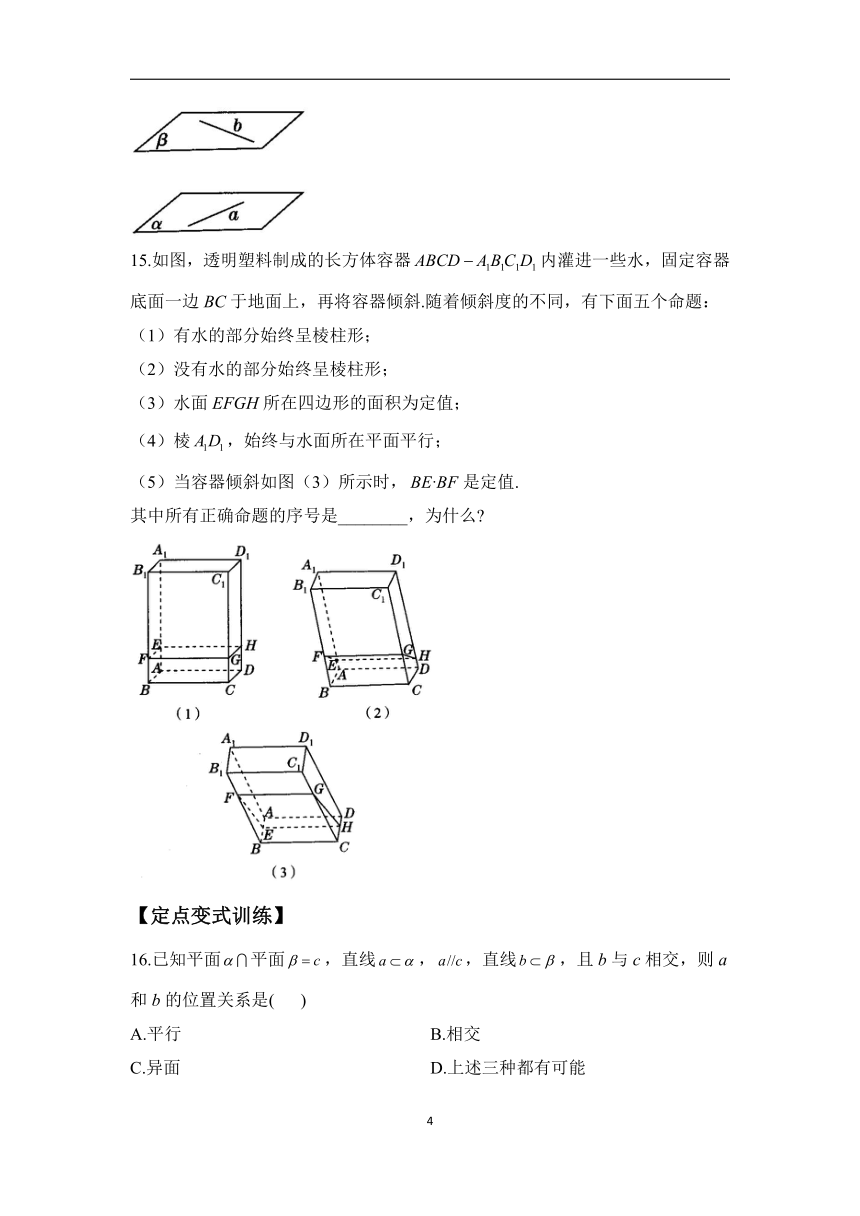
15.如图,透明塑料制成的长方体容器内灌进一些水,固定容器底面一边BC于地面上,再将容器倾斜.随着倾斜度的不同,有下面五个命题:
(1)有水的部分始终呈棱柱形;
(2)没有水的部分始终呈棱柱形;
(3)水面EFGH所在四边形的面积为定值;
(4)棱,始终与水面所在平面平行;
(5)当容器倾斜如图(3)所示时,是定值.
其中所有正确命题的序号是________,为什么
【定点变式训练】
16.已知平面平面,直线,,直线,且b与c相交,则a和b的位置关系是( )
A.平行 B.相交
C.异面 D.上述三种都有可能
17.如图,设E,F,G,H依次是空间四边形ABCD的边AB,BC,CD,DA上除端点外的点,且,,则下列结论不正确的是( )
A.当时,四边形EFGH是平行四边形
B.当时,四边形EFGH是梯形
C.当时,四边形EFGH是平行四边形
D.当时,四边形EFGH是梯形
18.如图,在各棱长均为1的正三棱柱中,M,N分别为线段,上的动点,且平面,则这样的MN有( )
A.1条 B.2条 C.3条 D.无数条
19.如图,在棱长为2的正方体中,M是的中点,P是侧面上的动点,且平面,则线段MP长度的取值范围是( )
A. B. C. D.
20.已知直线a和平面,那么能得出的一个条件是( )
A.存在一条直线b,且 B.存在一条直线b,且
C.存在一个平面,且 D.存在一个平面,且
21.如图,在三棱柱中,D是BC的中点,E是上一点,且平面,则的值为_______________.
22.如图是长方体被一平面所截得的几何体,四边形EFGH为截面,则四边形EFGH的形状为___________________.
23.如图,E是棱长为1的正方体的棱上的一点,且平面,则线段CE的长度为________________.
24.如图,在正方体中,P,Q分别是平面,平面的中心,证明:
(1)平面;
(2)平面平面.
25.如图所示,已知ABCD为梯形,,,M为线段PC上一点.
(1)设平面平面,证明:.
(2)在棱PC上是否存在点M,使得平面MBD?若存在,请确定点M的位置;若不存在,请说明理由.
答案以及解析
1.答案:(1)D
(2)C
解析:
2.答案:平行或相交
解析:
3.答案:见解析
解析:在面内,过点P作直线EF,使,分别交棱,于点E,F,则EF就是过点P与棱CD平行的直线.
4.答案:见解析
解析:证明:连接AC.在长方体中,,
四边形为平行四边形..
又E,F分别是AB,BC的中点,,.
5.答案:(1)见解析
(2)见解析
解析:(1)F,G分别是BC,CD的中点,
.
平面EFG,平面EFG,
平面EFG.
(2)E,F分别是AB,BC的中点,.
平面EFG,平面EFG,平面EFG.
6.答案:见解析
解析:在直线a上取一点O,过点O作,则由a与确定的平面即为所求.
理由:如答图,,,且,所以.
7.答案:见解析
解析:,.
,,.同理,于是.
8.答案:见解析
解析:与相交于点O,.
又,,,
,.
又平面,平面,
平面.同理可证平面.
又平面ABC,平面ABC,,
平面平面.
9.答案:见解析
解析:连接.
E,分别是AD,的中点,
.
又在长方体中,.
,.
四边形与都是平行四边形.
,.
.
10.答案:见解析
解析:如图,连接CD.
,A,B,C,D共面,
平面ABDC,平面ABDC,ABDC.
,,,
平面.
,,
四边形ABDC是平行四边形,.
11.答案:见解析
解析:如图,过直线a作平面,使.
,.
又,.
,,.
12.答案:见解析
解析:如图,过平面VAC内一点P作直线,交VA于点D,交VC于点E.
过平面VBA内一点D作直线,交AB丁点F,
过平面VBC内一点E作直线,交BC于点M,连接FM,则DE,DF,EM,MF就是应画线.
13.答案:见解析
解析:如图,连接AF交于点M,连接MB,CF,ME,AD.因为,平面,乎面,所以,所以.同理,且,所以.
14.答案:见解析
解析:过b作平面交于直线.因为,,,所以.因为,,所以.又a与相交,,所以.
15.答案:(1)(2)(4)(5),原因见解析
解析:原因:因为平面平面,所以有水的部分和无水的部分始终有两个面平行,而其余各面都易证是平行四边形,所以(1)(2)是正确的.在题图(1)中,水面面积,在题图(2)中,水面面积,而题图(1)中的EF小于题图(2)中的EF,则,所以(3)是错误的.易知(4)是正确的.因为水的体积一定,形成的柱体的高度始终是BC,所以底面的面积一定,即是一个定值,即是一个定值,所以(5)是正确的.
16.答案:C
解析:若a与b平行,因为,所以,与b与c相交矛盾,所以A错;若a和b相交,因为直线,直线,平面平面,则a,b,c相交于同一点处,这与矛盾,所以B错;因为两条直线的位置关系有平行,相交,异面这三种情况,故a和b只能异面.故选C.
17.答案:D
解析:如图所示,连接BD.,,且.同理,,且..当时,,四边形EFGH是平行四边形.选项A,C正确,D错.当时,,四边形EFGH是梯形,选项B正确.
18.答案:D
解析:如图,过线段上任一点M作,交AB于点H,过点H作交BC于点G,过点G作的平行线,与一定有交点N,且平面,则这样的MN有无数条.故选D.
19.答案:B
解析:取CD的中点N,的中点R,的中点H,连接MN,NR,MR,MH,RH,则,,平面平面,平面MNRH,线段MP扫过的图形是.,,,,,是直角.线段MP长度的取值范围是.故选B.
20.答案:C
解析:在选项A,B,D中,均有可能a在平面内,错误;在C中,两平面平行,则其中一个平面内的任意一条直线都平行于另一个平面,故C正确.
21.答案:
解析:连接交于点F,连接EF.因为平面平面,平面,所以,所以.因为,所以,所以.
因为D是BC的中点,所以,所以.
22.答案:平行四边形
解析:由题知,平面平面CDHG,平面平面,平面平面,所以.同理可得,所以四边形EFGH是平行四边形.
23.答案:
解析:如图,连接交于点O,连接EO,则O为的中点.因为平面,平面,平面平面,所以,故E为的中点,所以.在中,.故答案为.
24.答案:(1)见解析
(2)见解析
解析:(1)由题可知.
平面,平面,平面.
(2)由题可知.
平面,平面,平面.
由(1)知,平面,又,
平面平面.
25.答案:(1)见解析
(2)存在点M,使得平面MBD,此时,理由见解析
解析:(1)因为,平面PDC,平面PDC,
所以平面PDC.又因为平面平面,且平面PAB,所以.
(2)存在点M,使得平面MBD,
此时.理由如下:
连接AC交BD于点O,连接MO.
因为,所以.
又,所以.
又因为,,
所以.又因为平面MBD,平面MBD,
所以平面MBD.
2
【教材课后习题】
1.选择题
(1)若直线a不平行于平面,则下列结论成立的是( ).
A.内的所有直线都与a异面 B.内不存在与a平行的直线
C.内的直线都与a相交 D.直线a与平面有公共点
(2)如果直线平面,,那么过点P且平行于直线a的直线( ).
A.只有一条,不在平面内 B.有无数条,不一定在内
C.只有一条,且在平面内 D.有无数条,一定在内
2.已知平面和直线a,b,c,且,,,,则与的位置关系是_________.
3.如图,在长方体木块中,面上有一点P,怎样过点P画一条直线与棱CD平行
4.如图,在长方体中,E,F分别是AB,BC的中点,求证.
5.如图,在四面体中,E,F,G分别是AB,BC,CD的中点,求证:
(1)平面EFG;
(2)平面EFG.
6.如图,a,b是异面直线,画出平面,使,且,并说明理由.
7.如图,,,,,求证.
8.如图,直线,,相交于点O,,,求证:平面平面.
9.如图,E,分别为长方体的棱AD,的中点,求证.
10.如图,,,,,求证.
11.已知平面外的两条平行直线中的一条平行于这个平面,求证:另一条也平行于这个平面.
已知:,,,,
求证:.
12.一木块如图所示,点P在平面VAC内,过点P将木块锯开,使截面平行于直线VB和AC,在木块表面应该怎样画线?
13.如图,,直线a与b分别交于点A,B,C和点D,E,F,求证.
14.如图,a,b是异面直线,,,,,求证.
15.如图,透明塑料制成的长方体容器内灌进一些水,固定容器底面一边BC于地面上,再将容器倾斜.随着倾斜度的不同,有下面五个命题:
(1)有水的部分始终呈棱柱形;
(2)没有水的部分始终呈棱柱形;
(3)水面EFGH所在四边形的面积为定值;
(4)棱,始终与水面所在平面平行;
(5)当容器倾斜如图(3)所示时,是定值.
其中所有正确命题的序号是________,为什么
【定点变式训练】
16.已知平面平面,直线,,直线,且b与c相交,则a和b的位置关系是( )
A.平行 B.相交
C.异面 D.上述三种都有可能
17.如图,设E,F,G,H依次是空间四边形ABCD的边AB,BC,CD,DA上除端点外的点,且,,则下列结论不正确的是( )
A.当时,四边形EFGH是平行四边形
B.当时,四边形EFGH是梯形
C.当时,四边形EFGH是平行四边形
D.当时,四边形EFGH是梯形
18.如图,在各棱长均为1的正三棱柱中,M,N分别为线段,上的动点,且平面,则这样的MN有( )
A.1条 B.2条 C.3条 D.无数条
19.如图,在棱长为2的正方体中,M是的中点,P是侧面上的动点,且平面,则线段MP长度的取值范围是( )
A. B. C. D.
20.已知直线a和平面,那么能得出的一个条件是( )
A.存在一条直线b,且 B.存在一条直线b,且
C.存在一个平面,且 D.存在一个平面,且
21.如图,在三棱柱中,D是BC的中点,E是上一点,且平面,则的值为_______________.
22.如图是长方体被一平面所截得的几何体,四边形EFGH为截面,则四边形EFGH的形状为___________________.
23.如图,E是棱长为1的正方体的棱上的一点,且平面,则线段CE的长度为________________.
24.如图,在正方体中,P,Q分别是平面,平面的中心,证明:
(1)平面;
(2)平面平面.
25.如图所示,已知ABCD为梯形,,,M为线段PC上一点.
(1)设平面平面,证明:.
(2)在棱PC上是否存在点M,使得平面MBD?若存在,请确定点M的位置;若不存在,请说明理由.
答案以及解析
1.答案:(1)D
(2)C
解析:
2.答案:平行或相交
解析:
3.答案:见解析
解析:在面内,过点P作直线EF,使,分别交棱,于点E,F,则EF就是过点P与棱CD平行的直线.
4.答案:见解析
解析:证明:连接AC.在长方体中,,
四边形为平行四边形..
又E,F分别是AB,BC的中点,,.
5.答案:(1)见解析
(2)见解析
解析:(1)F,G分别是BC,CD的中点,
.
平面EFG,平面EFG,
平面EFG.
(2)E,F分别是AB,BC的中点,.
平面EFG,平面EFG,平面EFG.
6.答案:见解析
解析:在直线a上取一点O,过点O作,则由a与确定的平面即为所求.
理由:如答图,,,且,所以.
7.答案:见解析
解析:,.
,,.同理,于是.
8.答案:见解析
解析:与相交于点O,.
又,,,
,.
又平面,平面,
平面.同理可证平面.
又平面ABC,平面ABC,,
平面平面.
9.答案:见解析
解析:连接.
E,分别是AD,的中点,
.
又在长方体中,.
,.
四边形与都是平行四边形.
,.
.
10.答案:见解析
解析:如图,连接CD.
,A,B,C,D共面,
平面ABDC,平面ABDC,ABDC.
,,,
平面.
,,
四边形ABDC是平行四边形,.
11.答案:见解析
解析:如图,过直线a作平面,使.
,.
又,.
,,.
12.答案:见解析
解析:如图,过平面VAC内一点P作直线,交VA于点D,交VC于点E.
过平面VBA内一点D作直线,交AB丁点F,
过平面VBC内一点E作直线,交BC于点M,连接FM,则DE,DF,EM,MF就是应画线.
13.答案:见解析
解析:如图,连接AF交于点M,连接MB,CF,ME,AD.因为,平面,乎面,所以,所以.同理,且,所以.
14.答案:见解析
解析:过b作平面交于直线.因为,,,所以.因为,,所以.又a与相交,,所以.
15.答案:(1)(2)(4)(5),原因见解析
解析:原因:因为平面平面,所以有水的部分和无水的部分始终有两个面平行,而其余各面都易证是平行四边形,所以(1)(2)是正确的.在题图(1)中,水面面积,在题图(2)中,水面面积,而题图(1)中的EF小于题图(2)中的EF,则,所以(3)是错误的.易知(4)是正确的.因为水的体积一定,形成的柱体的高度始终是BC,所以底面的面积一定,即是一个定值,即是一个定值,所以(5)是正确的.
16.答案:C
解析:若a与b平行,因为,所以,与b与c相交矛盾,所以A错;若a和b相交,因为直线,直线,平面平面,则a,b,c相交于同一点处,这与矛盾,所以B错;因为两条直线的位置关系有平行,相交,异面这三种情况,故a和b只能异面.故选C.
17.答案:D
解析:如图所示,连接BD.,,且.同理,,且..当时,,四边形EFGH是平行四边形.选项A,C正确,D错.当时,,四边形EFGH是梯形,选项B正确.
18.答案:D
解析:如图,过线段上任一点M作,交AB于点H,过点H作交BC于点G,过点G作的平行线,与一定有交点N,且平面,则这样的MN有无数条.故选D.
19.答案:B
解析:取CD的中点N,的中点R,的中点H,连接MN,NR,MR,MH,RH,则,,平面平面,平面MNRH,线段MP扫过的图形是.,,,,,是直角.线段MP长度的取值范围是.故选B.
20.答案:C
解析:在选项A,B,D中,均有可能a在平面内,错误;在C中,两平面平行,则其中一个平面内的任意一条直线都平行于另一个平面,故C正确.
21.答案:
解析:连接交于点F,连接EF.因为平面平面,平面,所以,所以.因为,所以,所以.
因为D是BC的中点,所以,所以.
22.答案:平行四边形
解析:由题知,平面平面CDHG,平面平面,平面平面,所以.同理可得,所以四边形EFGH是平行四边形.
23.答案:
解析:如图,连接交于点O,连接EO,则O为的中点.因为平面,平面,平面平面,所以,故E为的中点,所以.在中,.故答案为.
24.答案:(1)见解析
(2)见解析
解析:(1)由题可知.
平面,平面,平面.
(2)由题可知.
平面,平面,平面.
由(1)知,平面,又,
平面平面.
25.答案:(1)见解析
(2)存在点M,使得平面MBD,此时,理由见解析
解析:(1)因为,平面PDC,平面PDC,
所以平面PDC.又因为平面平面,且平面PAB,所以.
(2)存在点M,使得平面MBD,
此时.理由如下:
连接AC交BD于点O,连接MO.
因为,所以.
又,所以.
又因为,,
所以.又因为平面MBD,平面MBD,
所以平面MBD.
2
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
