集合的运算---交、并[上学期]
文档属性
| 名称 | 集合的运算---交、并[上学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 45.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-09-26 00:00:00 | ||
图片预览

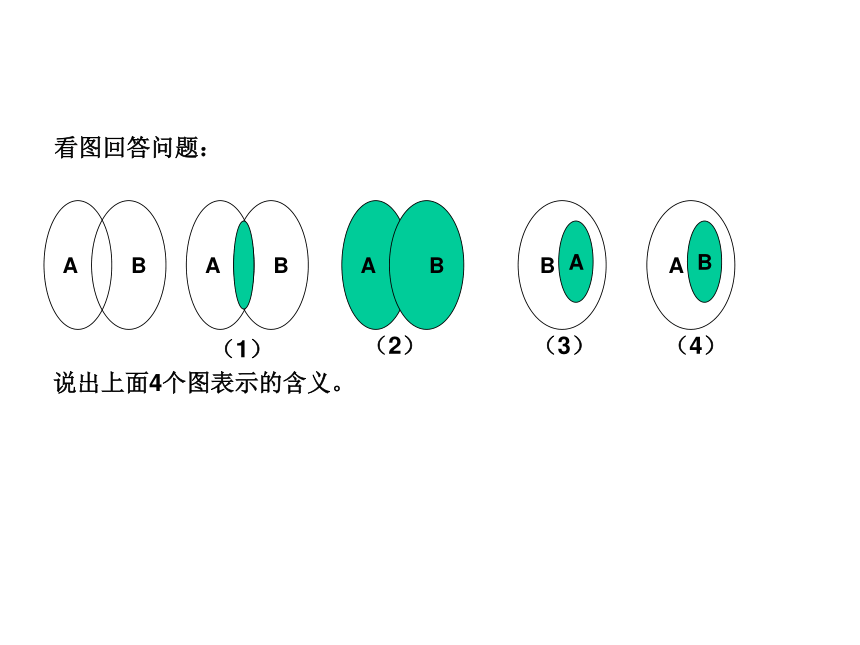
文档简介
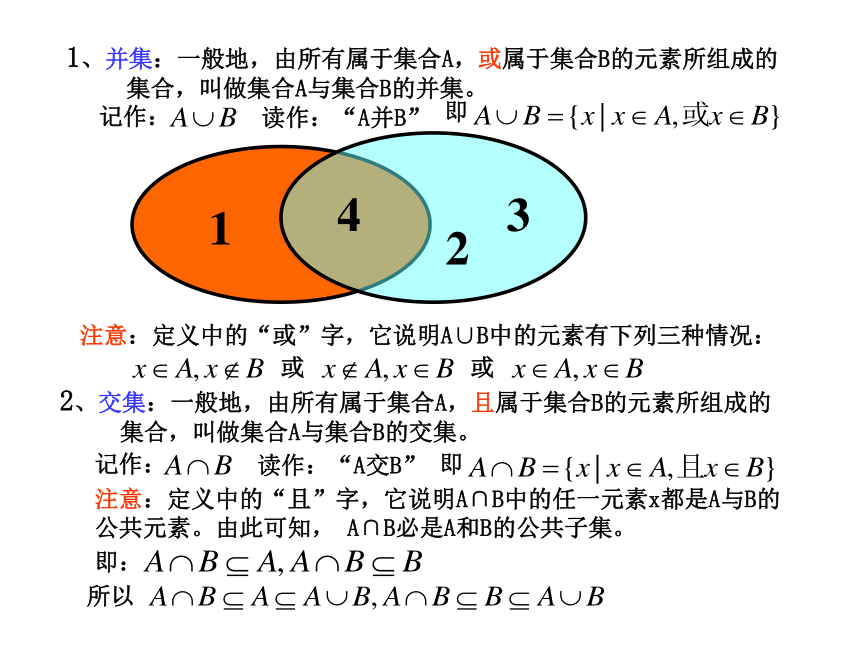
课件11张PPT。1.1.3集合的基本运算看图回答问题:说出上面4个图表示的含义。1、并集:一般地,由所有属于集合A,或属于集合B的元素所组成的
集合,叫做集合A与集合B的并集。注意:定义中的“或”字,它说明A∪B中的元素有下列三种情况:12342、交集:一般地,由所有属于集合A,且属于集合B的元素所组成的
集合,叫做集合A与集合B的交集。注意:定义中的“且”字,它说明A∩B中的任一元素x都是A与B的
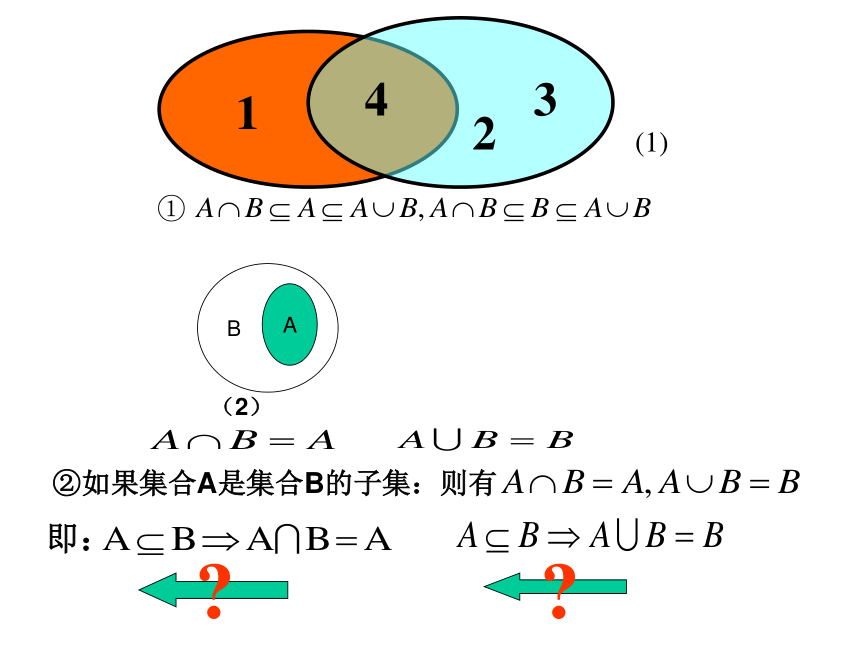
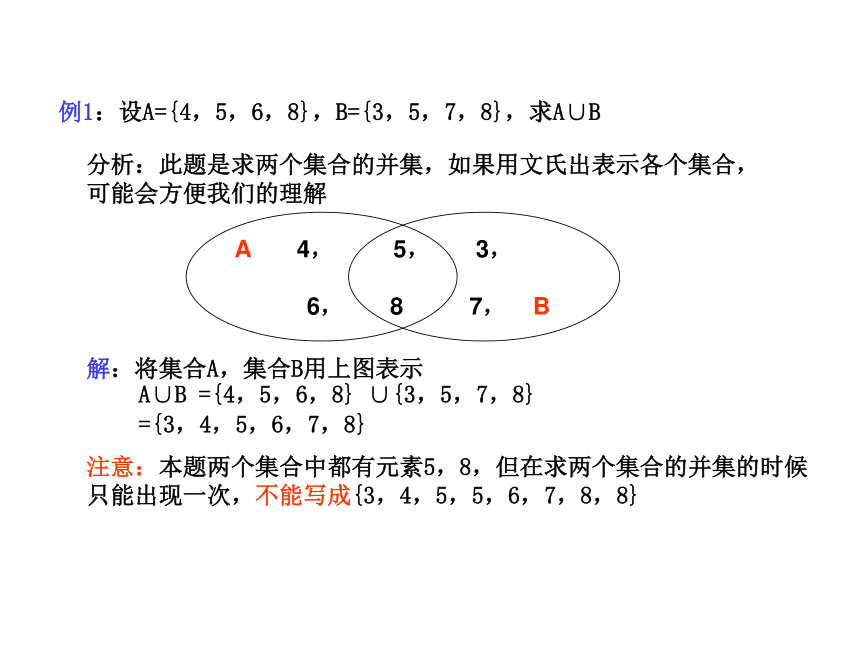
公共元素。由此可知, A∩B必是A和B的公共子集。例1:设A={4,5,6,8},B={3,5,7,8},求A∪B分析:此题是求两个集合的并集,如果用文氏出表示各个集合,
可能会方便我们的理解解:将集合A,集合B用上图表示A∪B ={4,5,6,8} ∪{3,5,7,8}
={3,4,5,6,7,8}注意:本题两个集合中都有元素5,8,但在求两个集合的并集的时候
只能出现一次,不能写成{3,4,5,5,6,7,8,8}例2:设A={x|x是锐角三角形},B={x|x是钝角三角形},求A∪B解:A∪B ={x|x是锐角三角形} ∪{x|x是钝角三角形}
={x|x是斜三角形}例3:设分析:此题与例1类似,与实数大小有关系,利用数轴处理解:将集合A,集合B用上图表示例4:设分析:求两个集合的交集即是求既属于集合A又属于集合B的元素,
此题与实数大小有关系,利用数轴处理会是问题简便解:在数轴上分别作出集合A 集合B所对应的部分从图形可以看出,阴影部分即是集合A 与集合B 的交集例5:设A={x|x是等腰三角形},B={x|x是直角三角形},求A∩B分析:此题仍是求交集,如果用文氏图表示各个集合,可能会
方便我们的理解解:将集合A,集合B用上图表示A∩B ={x|x是等腰三角形}∩{x|x是直角三角形}
={x|x是等腰直角三角形}经验总结:解集合问题时,元素是核心,所以在解集
合题时抓住元素特征是重要途径。
元素的三大特征:确定性、互异性、无序性。
方法:(1)利用集合间关系进行元素分析;
(2)利用文氏图进行元素分析;
(3)利用数轴进行元素分析。课堂小结:
1、正确理解交集与并集的概念。
2、会求两个已知集合的交集、并集。
3、文氏图在集合中的运用能力。
集合,叫做集合A与集合B的并集。注意:定义中的“或”字,它说明A∪B中的元素有下列三种情况:12342、交集:一般地,由所有属于集合A,且属于集合B的元素所组成的
集合,叫做集合A与集合B的交集。注意:定义中的“且”字,它说明A∩B中的任一元素x都是A与B的
公共元素。由此可知, A∩B必是A和B的公共子集。例1:设A={4,5,6,8},B={3,5,7,8},求A∪B分析:此题是求两个集合的并集,如果用文氏出表示各个集合,
可能会方便我们的理解解:将集合A,集合B用上图表示A∪B ={4,5,6,8} ∪{3,5,7,8}
={3,4,5,6,7,8}注意:本题两个集合中都有元素5,8,但在求两个集合的并集的时候
只能出现一次,不能写成{3,4,5,5,6,7,8,8}例2:设A={x|x是锐角三角形},B={x|x是钝角三角形},求A∪B解:A∪B ={x|x是锐角三角形} ∪{x|x是钝角三角形}
={x|x是斜三角形}例3:设分析:此题与例1类似,与实数大小有关系,利用数轴处理解:将集合A,集合B用上图表示例4:设分析:求两个集合的交集即是求既属于集合A又属于集合B的元素,
此题与实数大小有关系,利用数轴处理会是问题简便解:在数轴上分别作出集合A 集合B所对应的部分从图形可以看出,阴影部分即是集合A 与集合B 的交集例5:设A={x|x是等腰三角形},B={x|x是直角三角形},求A∩B分析:此题仍是求交集,如果用文氏图表示各个集合,可能会
方便我们的理解解:将集合A,集合B用上图表示A∩B ={x|x是等腰三角形}∩{x|x是直角三角形}
={x|x是等腰直角三角形}经验总结:解集合问题时,元素是核心,所以在解集
合题时抓住元素特征是重要途径。
元素的三大特征:确定性、互异性、无序性。
方法:(1)利用集合间关系进行元素分析;
(2)利用文氏图进行元素分析;
(3)利用数轴进行元素分析。课堂小结:
1、正确理解交集与并集的概念。
2、会求两个已知集合的交集、并集。
3、文氏图在集合中的运用能力。
