18.1.2平行四边形的判定(2) 课件(共36张PPT)
文档属性
| 名称 | 18.1.2平行四边形的判定(2) 课件(共36张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-23 19:08:59 | ||
图片预览




文档简介
(共36张PPT)
18.1.2平行四边形的判定(2)
人教版八年级下册
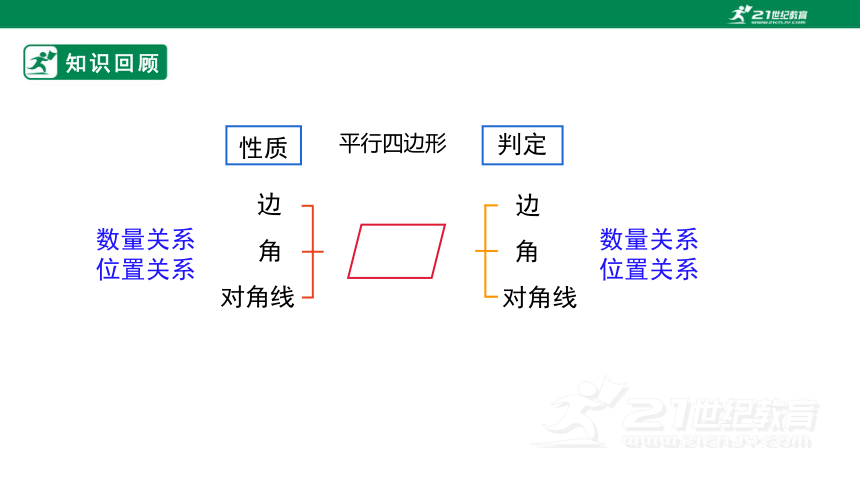
知识回顾
边
角
对角线
数量关系
位置关系
边
角
对角线
判定
性质
数量关系
位置关系
平行四边形
知识回顾
平行四边形的判定定理:
两组对边分别相等的四边形是平行四边形;
两组对角分别相等的四边形是平行四边形;
对角线互相平分的四边形是平行四边形.
平行四边形的定义:
两组对边分别平行的四边形是平行四边形.
1.掌握“一组对边平行且相等的四边形是平行四边形”
的判定方法.
2.会进行平行四边形的性质与判定的综合运用.
教学目标
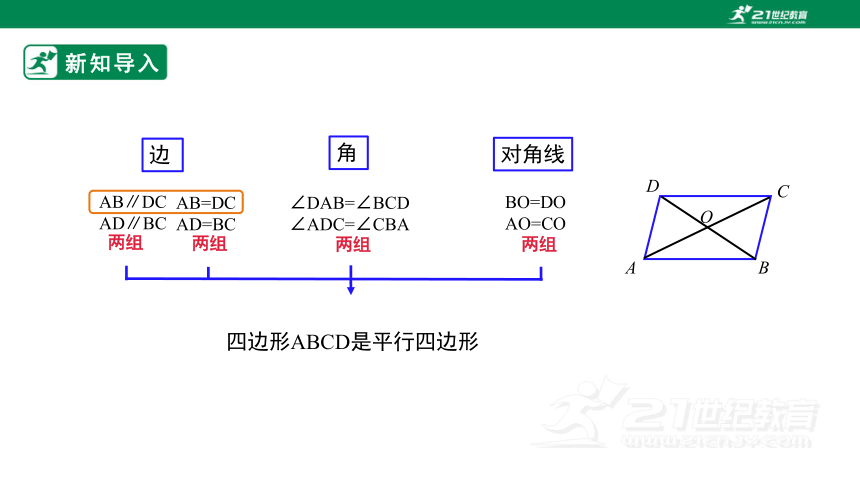
新知导入
D
A
C
B
O
AB∥DC
AD∥BC
四边形ABCD是平行四边形
边
AB=DC
AD=BC
角
∠DAB=∠BCD
∠ADC=∠CBA
对角线
BO=DO
AO=CO
两组
两组
两组
两组
新知探究
知识点
平行四边形的判定
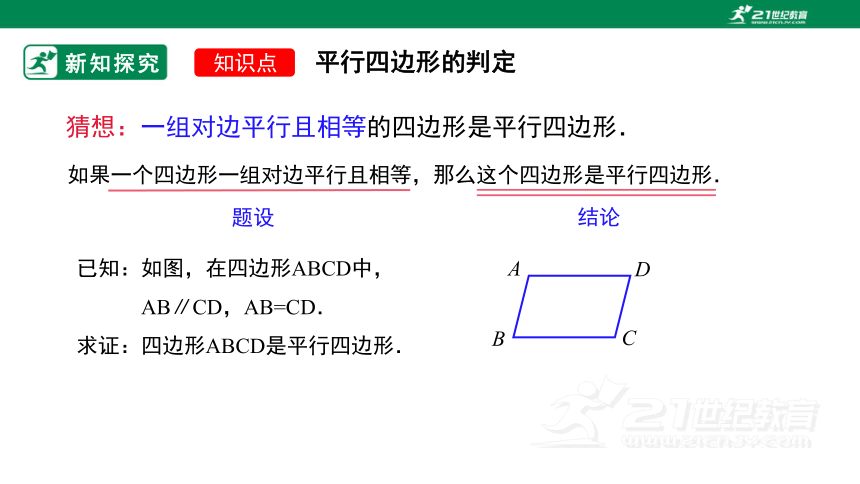
猜想:一组对边平行且相等的四边形是平行四边形.
如果一个四边形一组对边平行且相等,那么这个四边形是平行四边形.
题设
结论
已知:如图,在四边形ABCD中,
AB∥CD,AB=CD.
求证:四边形ABCD是平行四边形.
D
A
B
C
新知探究
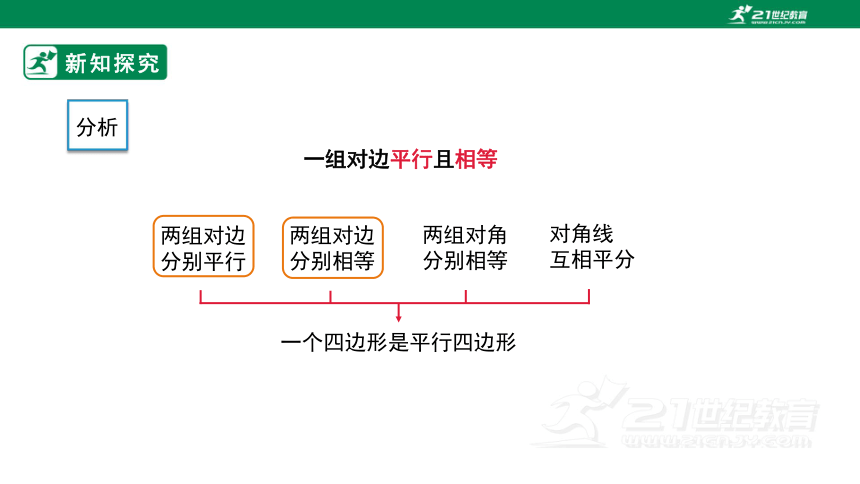
分析
两组对边
分别平行
一个四边形是平行四边形
两组对边
分别相等
两组对角
分别相等
对角线
互相平分
一组对边平行且相等
新知探究
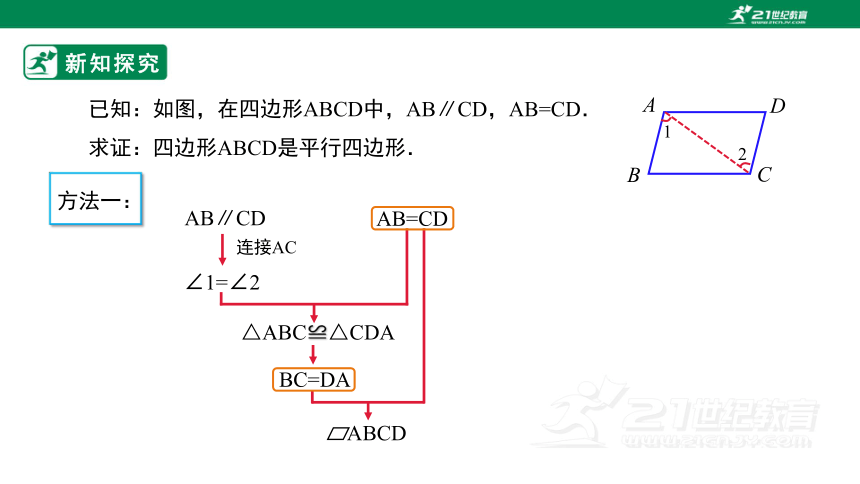
已知:如图,在四边形ABCD中,AB∥CD,AB=CD.
求证:四边形ABCD是平行四边形.
D
A
B
C
BC=DA
AB∥CD
1
2
方法一:
AB=CD
△ABC≌△CDA
∠1=∠2
连接AC
ABCD
新知探究
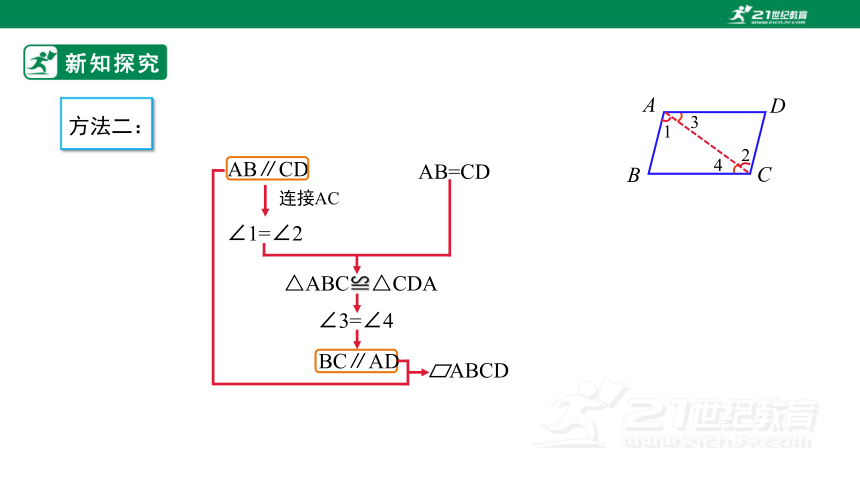
∠3=∠4
AB∥CD
△ABC≌△CDA
∠1=∠2
连接AC
4
3
BC∥AD
AB=CD
方法二:
D
A
B
C
1
2
ABCD
新知探究
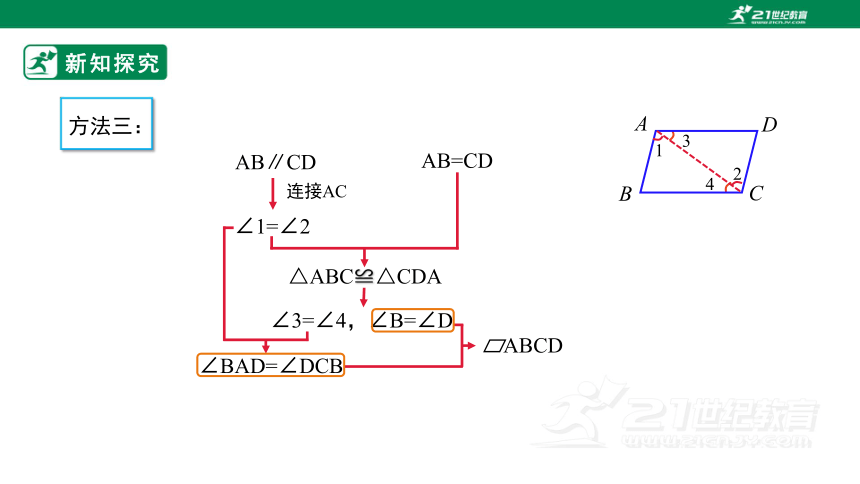
连接AC
△ABC≌△CDA
∠3=∠4,∠B=∠D
AB∥CD
∠1=∠2
∠BAD=∠DCB
AB=CD
方法三:
4
3
D
A
B
C
1
2
ABCD
新知探究
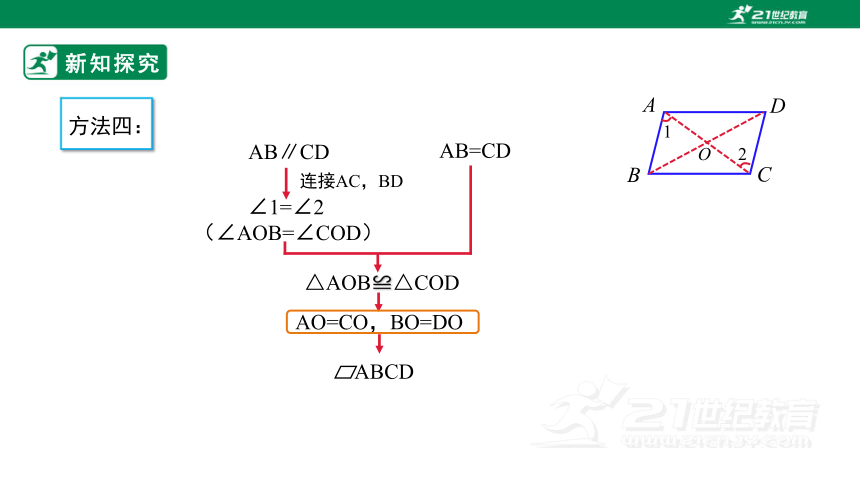
连接AC,BD
△AOB≌△COD
AO=CO,BO=DO
AB∥CD
∠1=∠2
(∠AOB=∠COD)
O
AB=CD
方法四:
ABCD
D
A
B
C
1
2
新知探究
例 如图,在四边形ABCD中,AB//CD,AB=CD. 求证:四边形ABCD 是平行四边形.
A
B
C
D
证明:连接AC
∵ AB//CD ∴∠1=∠2
又 AB=CD,AC=CA
∴ △ABC ≌△CDA,BC=AD
∴四边形ABCD是平行四边形
∵ AB=CD BC=AD
1
2
方法一:
新知探究
平行四边形的判定5:
一组对边平行且相等的四边形是平行四边形.
A
B
C
D
数学语言:
∵ AB//CD,AB=CD,
∴四边形ABCD是平行四边形
例4 如图,在 中,E,F分别是AB,CD的中点.
求证:四边形EBFD是平行四边形.
ABCD
新知探究
A
B
C
D
E
F
新知探究
分析
E是AB中点
F是CD中点
EB∥FD
EB=AB,FD= CD
EB=FD
EBFD
ABCD
AB=CD,AB∥CD
新知探究
例4 如图,在平行四边形ABCD中,E、F分别是AB、CD的中点.
求证:四边形EBFD是平行四边形.
A
B
C
D
E
F
证明: ∵四边形ABCD是平行四边形
∴ AB=CD, EB//FD
∵ E、F分别是AB、CD的中点
∴ EB
∴ EB=FD
∴四边形EBFD是平行四边形
新知小结
四边形
边
角
对角线
两组对边分别平行
两组对边分别相等
一组对边平行且相等
两组对角分别相等
对角线互相平分
平行四边形
平行四边形的判定方法
新知练习
1. 如图,AD为△ABC的角平分线,DE∥AB,在AB上截取BF=AE,试猜想EF与BD的关系,并证明你的结论.
A
B
E
F
C
D
AD为△ABC
的角平分线
分析
DE∥AB
∠BAD=∠DAC
∠BAD=∠ADE
∠DAC=∠ADE
AE=DE
(已知)
(已知)
新知练习
BF=AE
AE=DE
BF=DE,
DE∥AB
(已知)
BF∥DE
EF=BD, EF∥BD
(已证)
分析
1. 如图,AD为△ABC的角平分线,DE∥AB,在AB上截取BF=AE,试猜想EF与BD的关系,并证明你的结论.
BDEF
A
B
E
F
C
D
新知练习
猜想:EF=BD,EF∥BD.
证明:∵ AD平分∠BAC,
∴ ∠BAD=∠DAC.
∵ DE∥AB,
∴ ∠BAD=∠ADE.
∴ ∠DAC=∠ADE.
∴ AE=DE.
A
B
E
F
C
D
1. 如图,AD为△ABC的角平分线,DE∥AB,在AB上截取BF=AE,试猜想EF与BD的关系,并证明你的结论.
新知探究
∵ BF=AE,
∴ BF=DE.
又 BF∥DE,
∴ 四边形BDEF是平行四边形.
∴ EF=BD,EF∥BD.
1. 如图,AD为△ABC的角平分线,DE∥AB,在AB上截取BF=AE,试猜想EF与BD的关系,并证明你的结论.
A
B
E
F
C
D
新知练习
2.如图,在平行四边形ABCD中,BD是它的一条对角线,过A,C两点分别作AE⊥BD,CF⊥BD,E,F为垂足.
求证:四边形AFCE是平行四边形.
AE∥CF
思路一
一组对边平行且相等
对角线BD
AE⊥BD,CF⊥BD
思路二
对角线互相平分
点E,F在BD上
新知练习
方法一:
□AFCE
AE∥CF
AE=CF
(已知)
AE⊥BD
CF⊥BD
∠AEF=∠CFE=90°
∠AED=∠CFB=90°
AD∥BC
∠ADB=∠CBD
AD=BC
△AED≌△CFB
ABCD(已知)
新知练习
证明:∵ 四边形ABCD是平行四边形,
∴ AD∥BC,AD=BC.
∴ ∠ADB=∠CBD.
∵ AE⊥BD,CF⊥BD,
∴ ∠AEF=∠CFE=90°,
∠AED=∠CFB=90°.
2.如图,在平行四边形ABCD中,BD是它的一条对角线,过A,C两点分别作AE⊥BD,CF⊥BD,E,F为垂足.
求证:四边形AFCE是平行四边形.
新知练习
∴ △AED≌△CFB(AAS).
∴ AE=CF.
又 ∠AEF=∠CFE,
∴ AE∥CF.
∴ 四边形AFCE是平行四边形.
2.如图,在平行四边形ABCD中,BD是它的一条对角线,过A,C两点分别作AE⊥BD,CF⊥BD,E,F为垂足.
求证:四边形AFCE是平行四边形.
新知练习
AO=CO
(∠AOE=∠COF)
EO=FO
△AEO≌△CFO
(已知)
AE⊥BD
CF⊥BD
连接AC
方法二:
∠AEO=∠CFO
ABCD
(已知)
AFCE
O
新知练习
证明:连接AC交BD于点O.
∵ 四边形ABCD是平行四边形,
∴ AO=CO.
∵ AE⊥BD,CF⊥BD,
∴ ∠AEO=∠CFO=90°.
2.如图,在平行四边形ABCD中,BD是它的一条对角线,过A,C两点分别作AE⊥BD,CF⊥BD,E,F为垂足.
求证:四边形AFCE是平行四边形.
O
新知练习
∵ ∠AOE=∠COF,
∴ △AEO≌△CFO.
∴ EO=FO.
∴ 四边形AFCE是平行四边形.
2.如图,在平行四边形ABCD中,BD是它的一条对角线,过A,C两点分别作AE⊥BD,CF⊥BD,E,F为垂足.
求证:四边形AFCE是平行四边形.
课堂总结
平行四边形的判定
判定5
数学
语言
一组对边平行且相等的四边形是平行四边形.
∵ AB//CD,AB=CD,
∴四边形ABCD是平行四边形
课堂练习
1.如图,在四边形ABCD中,AB∥CD,要使四边形ABCD是平行四边形,可添加的条件不正确的是( )
A.AB=CD
B.BC=AD
C.∠A=∠C
D.BC∥AD
A
B
C
D
一组对边平行且相等
两组对边分别平行
∠B+∠C=180°
∠B+∠A=180°
AD//BC
B
课堂练习
2.如图,在四边形ABCD中,对角线 AC、BD 相交于点 O,OA=OC. BA⊥AC,DC⊥AC. 求证:四边形 ABCD 是平行四边形.
解析:通过两个垂直可以得到 AB//CD,通过三角形的全等能得到 AB=CD .
A
C
D
B
┐
┐
O
课堂练习
证明:∵ BA⊥AC,DC⊥AC
∴∠BAC=∠DCA=90
∴ △AOB≌△COD,AB=CD
∴四边形ABCD是平行四边形
∵在△AOB和△COD中,∠BAC=∠DCA,OA=OC,
∠AOB=∠COD
∵∠BAC=∠DCA=90
∴ AB//CD
A
C
D
B
┐
┐
O
课堂练习
3.如图,在平行四边形ABCD中,E、F 分别是AB、CD的中点.求证:EF//AD//BC.
B
C
A
D
E
F
证明: ∵四边形ABCD是平行四边形
∴AB=CD,AB//CD
∵ E、F分别是AB、CD的中点
∴AE=DF,AE//DF
∴四边形AEFD是平行四边形
∴ AD//EF
∵ AD//BC
∴ EF//AD//BC
课堂练习
4.如图,四边形ABCD和四边形AEFD都是平行四边形,求证:四边形BCFE是平行四边形.
B
C
A
D
E
F
证明: ∵四边形ABCD是平行四边形
∴AD=BC,AD//BC
∵四边形AEFD是平行四边形
∴AD=EF,AD//EF
∴BC=EF,BC//EF
∴四边形BCFE是平行四边形
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
18.1.2平行四边形的判定(2)
人教版八年级下册
知识回顾
边
角
对角线
数量关系
位置关系
边
角
对角线
判定
性质
数量关系
位置关系
平行四边形
知识回顾
平行四边形的判定定理:
两组对边分别相等的四边形是平行四边形;
两组对角分别相等的四边形是平行四边形;
对角线互相平分的四边形是平行四边形.
平行四边形的定义:
两组对边分别平行的四边形是平行四边形.
1.掌握“一组对边平行且相等的四边形是平行四边形”
的判定方法.
2.会进行平行四边形的性质与判定的综合运用.
教学目标
新知导入
D
A
C
B
O
AB∥DC
AD∥BC
四边形ABCD是平行四边形
边
AB=DC
AD=BC
角
∠DAB=∠BCD
∠ADC=∠CBA
对角线
BO=DO
AO=CO
两组
两组
两组
两组
新知探究
知识点
平行四边形的判定
猜想:一组对边平行且相等的四边形是平行四边形.
如果一个四边形一组对边平行且相等,那么这个四边形是平行四边形.
题设
结论
已知:如图,在四边形ABCD中,
AB∥CD,AB=CD.
求证:四边形ABCD是平行四边形.
D
A
B
C
新知探究
分析
两组对边
分别平行
一个四边形是平行四边形
两组对边
分别相等
两组对角
分别相等
对角线
互相平分
一组对边平行且相等
新知探究
已知:如图,在四边形ABCD中,AB∥CD,AB=CD.
求证:四边形ABCD是平行四边形.
D
A
B
C
BC=DA
AB∥CD
1
2
方法一:
AB=CD
△ABC≌△CDA
∠1=∠2
连接AC
ABCD
新知探究
∠3=∠4
AB∥CD
△ABC≌△CDA
∠1=∠2
连接AC
4
3
BC∥AD
AB=CD
方法二:
D
A
B
C
1
2
ABCD
新知探究
连接AC
△ABC≌△CDA
∠3=∠4,∠B=∠D
AB∥CD
∠1=∠2
∠BAD=∠DCB
AB=CD
方法三:
4
3
D
A
B
C
1
2
ABCD
新知探究
连接AC,BD
△AOB≌△COD
AO=CO,BO=DO
AB∥CD
∠1=∠2
(∠AOB=∠COD)
O
AB=CD
方法四:
ABCD
D
A
B
C
1
2
新知探究
例 如图,在四边形ABCD中,AB//CD,AB=CD. 求证:四边形ABCD 是平行四边形.
A
B
C
D
证明:连接AC
∵ AB//CD ∴∠1=∠2
又 AB=CD,AC=CA
∴ △ABC ≌△CDA,BC=AD
∴四边形ABCD是平行四边形
∵ AB=CD BC=AD
1
2
方法一:
新知探究
平行四边形的判定5:
一组对边平行且相等的四边形是平行四边形.
A
B
C
D
数学语言:
∵ AB//CD,AB=CD,
∴四边形ABCD是平行四边形
例4 如图,在 中,E,F分别是AB,CD的中点.
求证:四边形EBFD是平行四边形.
ABCD
新知探究
A
B
C
D
E
F
新知探究
分析
E是AB中点
F是CD中点
EB∥FD
EB=AB,FD= CD
EB=FD
EBFD
ABCD
AB=CD,AB∥CD
新知探究
例4 如图,在平行四边形ABCD中,E、F分别是AB、CD的中点.
求证:四边形EBFD是平行四边形.
A
B
C
D
E
F
证明: ∵四边形ABCD是平行四边形
∴ AB=CD, EB//FD
∵ E、F分别是AB、CD的中点
∴ EB
∴ EB=FD
∴四边形EBFD是平行四边形
新知小结
四边形
边
角
对角线
两组对边分别平行
两组对边分别相等
一组对边平行且相等
两组对角分别相等
对角线互相平分
平行四边形
平行四边形的判定方法
新知练习
1. 如图,AD为△ABC的角平分线,DE∥AB,在AB上截取BF=AE,试猜想EF与BD的关系,并证明你的结论.
A
B
E
F
C
D
AD为△ABC
的角平分线
分析
DE∥AB
∠BAD=∠DAC
∠BAD=∠ADE
∠DAC=∠ADE
AE=DE
(已知)
(已知)
新知练习
BF=AE
AE=DE
BF=DE,
DE∥AB
(已知)
BF∥DE
EF=BD, EF∥BD
(已证)
分析
1. 如图,AD为△ABC的角平分线,DE∥AB,在AB上截取BF=AE,试猜想EF与BD的关系,并证明你的结论.
BDEF
A
B
E
F
C
D
新知练习
猜想:EF=BD,EF∥BD.
证明:∵ AD平分∠BAC,
∴ ∠BAD=∠DAC.
∵ DE∥AB,
∴ ∠BAD=∠ADE.
∴ ∠DAC=∠ADE.
∴ AE=DE.
A
B
E
F
C
D
1. 如图,AD为△ABC的角平分线,DE∥AB,在AB上截取BF=AE,试猜想EF与BD的关系,并证明你的结论.
新知探究
∵ BF=AE,
∴ BF=DE.
又 BF∥DE,
∴ 四边形BDEF是平行四边形.
∴ EF=BD,EF∥BD.
1. 如图,AD为△ABC的角平分线,DE∥AB,在AB上截取BF=AE,试猜想EF与BD的关系,并证明你的结论.
A
B
E
F
C
D
新知练习
2.如图,在平行四边形ABCD中,BD是它的一条对角线,过A,C两点分别作AE⊥BD,CF⊥BD,E,F为垂足.
求证:四边形AFCE是平行四边形.
AE∥CF
思路一
一组对边平行且相等
对角线BD
AE⊥BD,CF⊥BD
思路二
对角线互相平分
点E,F在BD上
新知练习
方法一:
□AFCE
AE∥CF
AE=CF
(已知)
AE⊥BD
CF⊥BD
∠AEF=∠CFE=90°
∠AED=∠CFB=90°
AD∥BC
∠ADB=∠CBD
AD=BC
△AED≌△CFB
ABCD(已知)
新知练习
证明:∵ 四边形ABCD是平行四边形,
∴ AD∥BC,AD=BC.
∴ ∠ADB=∠CBD.
∵ AE⊥BD,CF⊥BD,
∴ ∠AEF=∠CFE=90°,
∠AED=∠CFB=90°.
2.如图,在平行四边形ABCD中,BD是它的一条对角线,过A,C两点分别作AE⊥BD,CF⊥BD,E,F为垂足.
求证:四边形AFCE是平行四边形.
新知练习
∴ △AED≌△CFB(AAS).
∴ AE=CF.
又 ∠AEF=∠CFE,
∴ AE∥CF.
∴ 四边形AFCE是平行四边形.
2.如图,在平行四边形ABCD中,BD是它的一条对角线,过A,C两点分别作AE⊥BD,CF⊥BD,E,F为垂足.
求证:四边形AFCE是平行四边形.
新知练习
AO=CO
(∠AOE=∠COF)
EO=FO
△AEO≌△CFO
(已知)
AE⊥BD
CF⊥BD
连接AC
方法二:
∠AEO=∠CFO
ABCD
(已知)
AFCE
O
新知练习
证明:连接AC交BD于点O.
∵ 四边形ABCD是平行四边形,
∴ AO=CO.
∵ AE⊥BD,CF⊥BD,
∴ ∠AEO=∠CFO=90°.
2.如图,在平行四边形ABCD中,BD是它的一条对角线,过A,C两点分别作AE⊥BD,CF⊥BD,E,F为垂足.
求证:四边形AFCE是平行四边形.
O
新知练习
∵ ∠AOE=∠COF,
∴ △AEO≌△CFO.
∴ EO=FO.
∴ 四边形AFCE是平行四边形.
2.如图,在平行四边形ABCD中,BD是它的一条对角线,过A,C两点分别作AE⊥BD,CF⊥BD,E,F为垂足.
求证:四边形AFCE是平行四边形.
课堂总结
平行四边形的判定
判定5
数学
语言
一组对边平行且相等的四边形是平行四边形.
∵ AB//CD,AB=CD,
∴四边形ABCD是平行四边形
课堂练习
1.如图,在四边形ABCD中,AB∥CD,要使四边形ABCD是平行四边形,可添加的条件不正确的是( )
A.AB=CD
B.BC=AD
C.∠A=∠C
D.BC∥AD
A
B
C
D
一组对边平行且相等
两组对边分别平行
∠B+∠C=180°
∠B+∠A=180°
AD//BC
B
课堂练习
2.如图,在四边形ABCD中,对角线 AC、BD 相交于点 O,OA=OC. BA⊥AC,DC⊥AC. 求证:四边形 ABCD 是平行四边形.
解析:通过两个垂直可以得到 AB//CD,通过三角形的全等能得到 AB=CD .
A
C
D
B
┐
┐
O
课堂练习
证明:∵ BA⊥AC,DC⊥AC
∴∠BAC=∠DCA=90
∴ △AOB≌△COD,AB=CD
∴四边形ABCD是平行四边形
∵在△AOB和△COD中,∠BAC=∠DCA,OA=OC,
∠AOB=∠COD
∵∠BAC=∠DCA=90
∴ AB//CD
A
C
D
B
┐
┐
O
课堂练习
3.如图,在平行四边形ABCD中,E、F 分别是AB、CD的中点.求证:EF//AD//BC.
B
C
A
D
E
F
证明: ∵四边形ABCD是平行四边形
∴AB=CD,AB//CD
∵ E、F分别是AB、CD的中点
∴AE=DF,AE//DF
∴四边形AEFD是平行四边形
∴ AD//EF
∵ AD//BC
∴ EF//AD//BC
课堂练习
4.如图,四边形ABCD和四边形AEFD都是平行四边形,求证:四边形BCFE是平行四边形.
B
C
A
D
E
F
证明: ∵四边形ABCD是平行四边形
∴AD=BC,AD//BC
∵四边形AEFD是平行四边形
∴AD=EF,AD//EF
∴BC=EF,BC//EF
∴四边形BCFE是平行四边形
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
