5.2运动的合成和分解(含答案)
文档属性
| 名称 | 5.2运动的合成和分解(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 169.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-02-23 18:08:55 | ||
图片预览




文档简介
5.2运动的合成和分解
、单选题
关于两个运动的合成,下列说法正确的是( )
A.两个直线运动的合运动一定也是直线运动
B.方向不共线的两个匀速直线运动的合运动一定也是匀速直线运动
C.小船渡河的运动中,小船的对地速度一定大于水流速度
D.小船渡河的运动中,水流速度越大,小船渡河所需时间越短
小船以一定的速度垂直河岸向对岸航行时,下列说法正确的是( )
A.水流速度越大,小船运动的位移越长,时间不变
B.水流速度越大,小船运动的位移越长,时间越短
C.水流速度越大,小船运动的位移越长,时间越长
D.水流速度越大,小船运动的位移和时间都不变
一只小船在静水中的速度始终为 ,若在流速为 的河中航行,则站在河岸上的人看到船的实际航速可能是( )
A.
一物体在以xOy为直角坐标系的平面上运动,其运动规律为x=-2t2-4t,y=3t2+6t(式中的物理量单位均为国际单位),关于物体的运动,下列说法正确的是( )
A.物体在x轴方向上做匀减速直线运动
B.物体运动的轨迹是一条直线
C.物体在y轴方向上做变加速直线运动
D.物体运动的轨迹是一条曲线
如图所示,船从A处开出后沿直线到达对岸,若 A与河岸成30° 角,水流速度为4m/s ,则船从A点开出的最小速度为( )
A.2m/s B.2.4m/s C.3m/s D.3.5m/s
一条小船在静水中的速度为,它要渡过一条宽为的河,河水流速为,下列说法正确的是( )
A.小船过河的最短位移为
B.小船以最短时间过河,其位移为
C.小船过河的实际速度可以垂直于河岸
D.若小船在静水中的速度垂直河岸且保持不变,而水速的大小变化,则小船运动轨迹为直线
如图所示,物体A和B的质量均为m,分别与跨过定滑轮的轻绳连接(不计绳与滑轮、滑轮与轴之间的摩擦)。现用水平变力F拉着物体A沿水平方向向右做匀速直线运动。则下列说法中正确的是( )
A.物体B做匀速直线运动 B.物体B做加速直线运动
C.物体B做减速直线运动 D.无法判断
如图所示,有一长为80cm的玻璃管竖直放置,当红蜡块从玻璃管的最下端开始匀速上升的同时,玻璃管水平向右匀速运动.经过20s,红蜡块到达玻璃管的最上端,此过程玻璃管的水平位移为60cm.不计红蜡块的大小,则红蜡块运动的合速度大小为( )
A.3cm/s B.4cm/s C.5cm/s D.7cm/s
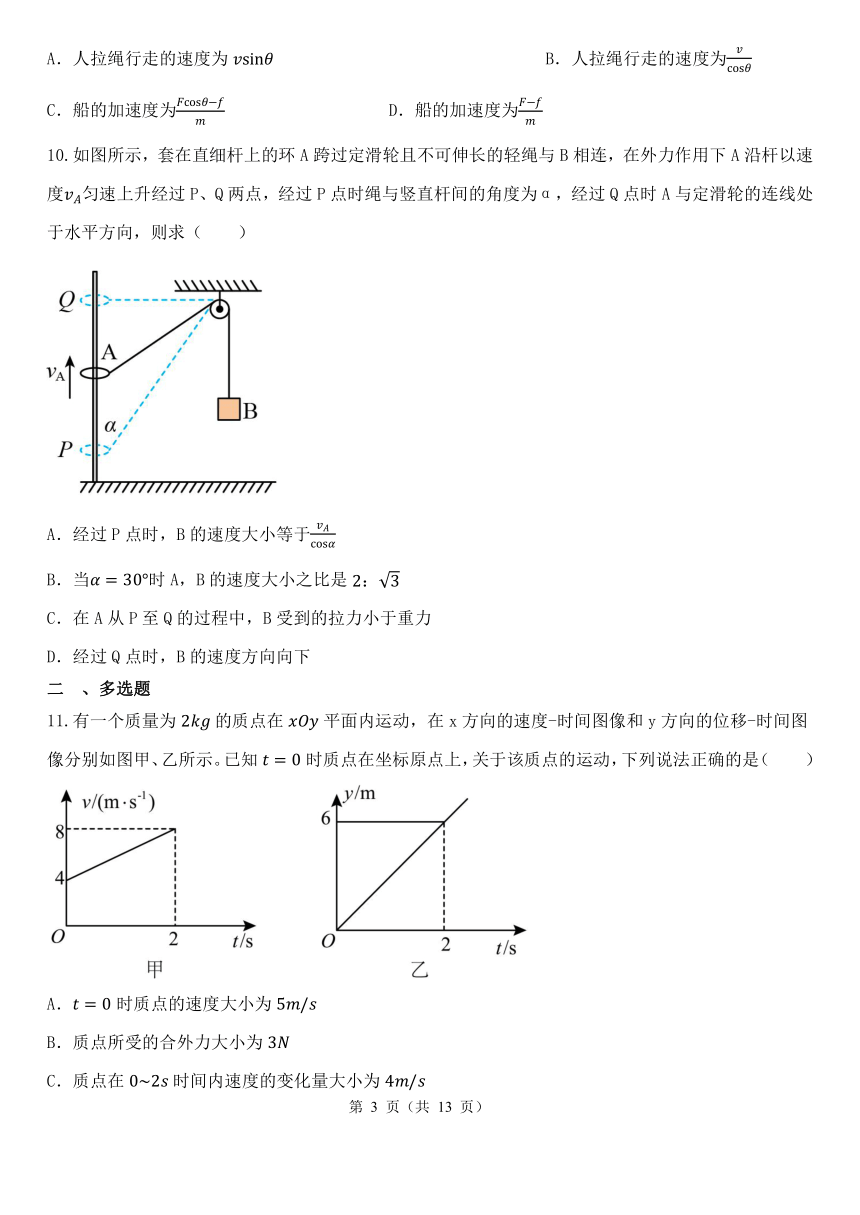
如图所示,人在岸上拉船,已知船的质量为m,水的阻力恒为f,当轻绳与水面的夹角为时,船的速度为v,人的拉力大小为F,则此时( )
A.人拉绳行走的速度为 B.人拉绳行走的速度为
C.船的加速度为 D.船的加速度为
如图所示,套在直细杆上的环A跨过定滑轮且不可伸长的轻绳与B相连,在外力作用下A沿杆以速度匀速上升经过P、Q两点,经过P点时绳与竖直杆间的角度为α,经过Q点时A与定滑轮的连线处于水平方向,则求( )
A.经过P点时,B的速度大小等于
B.当时A,B的速度大小之比是
C.在A从P至Q的过程中,B受到的拉力小于重力
D.经过Q点时,B的速度方向向下
、多选题
有一个质量为的质点在平面内运动,在x方向的速度-时间图像和y方向的位移-时间图像分别如图甲、乙所示。已知时质点在坐标原点上,关于该质点的运动,下列说法正确的是( )
A.时质点的速度大小为
B.质点所受的合外力大小为
C.质点在时间内速度的变化量大小为
D.质点的运动轨迹是一条直线
如图所示,一条小船过河,河宽d=120m,河水流速v1=3m/s,船在静水中速度v2=4m/s,关于小船的运动,以下说法正确的是( )
A.小船合运动的速度大小一定是5 m/s
B.小船渡河的最短时间为30 s
C.小船若以最短时间渡河,则其实际运动轨迹与河岸垂直
D.小船实际运动轨迹的最短位移是120 m
有一个质量为3kg的质点在xOy平面上运动,在x方向的速度图象和y方向的位移图象分别如图甲、乙所示,下列说法正确的是( )
A.质点的初速度为3m/s
B.质点所受的合外力为6N
C.质点1秒末的位移为 m
D.质点初速度的方向与合外力的方向垂直
、解答题
小物块置于倾角 =45°的固定光滑斜面靠近斜面底端的C点,轻细绳跨过光滑定滑轮分别连接着小物块与动力小车,滑轮到地面的距离h=4m,小物块与滑轮间的细绳平行于斜面,小车带动小物块使其以速度 m/s沿斜面向上做匀速直线运动,小车从A点到B点的过程中,连接小车的细绳与水平方向的夹角由 变化到 。已知sin53°=0.8,小物块和小车均可视为质点。求:
(1)小车在A点时的速度大小vA;
(2)小车从A点运动到B点的时间t。
一只船在200m宽的河中横渡,水流速度是2m/s,船在静水中的航速是4m/s,则
(1)小船怎样才能以最短时间渡过河去?需时多少?
(2)小船怎样才能以最短路径渡过河去 需时多少?
5.2运动的合成和分解答案解析
、单选题
【答案】B
【解析】【解答】两个分运动是直线运动,其合运动可能是曲线运动,比如平抛运动.A不符合题意.不共线两个匀速直线运动,没有加速度,则合运动也一定是匀速直线运动.B符合题意.合运动的速度(小船对地速度)可能比分速度(水流速度)大,可能比分速度小,可能与分速度相等.C不符合题意;小船渡河的时间由小船沿垂直于河岸方向的速度决定,故水流速度越大,小船渡河所需时间却不变,D不符合题意.
故答案为:B.
【分析】位移、速度、加速度都是矢量,合成分解遵循平行四边形定则.合运动与分运动具有等时性.
【答案】A
【解析】【解答】设河宽为d,船垂直于河岸的速度为v,河流的速度为v1
时间与水速无关;合速度为
运动位移
其中t不变,v不变,则河流的速度v1越大,位移越长;
故答案为:A.
【分析】当船头垂直于河岸时,渡河时间最短,与水流速度无关,利用速度的合成以及匀速直线运动的规律得出河流速度和位移的关系。
【答案】B
【解析】【解答】由平行四边形定则可得出其合速度的范围是大于或等于2m/s小于或等于8m/s,其间的任一速度值都有可能,则B符合题意,ACD不在其范围之内错误。
故答案为:B。
【分析】速度的合成遵循平行四边形定则,已知两个速度的大小和方向,利用平行四边形定则求解合速度即可。
【答案】B
【解析】【解答】A.根据匀变速直线运动的规律 可知 方向初速度和加速度分别为
速度与加速度同向,物体在x轴方向上做匀加速直线运动,A不符合题意;
B. 方向初速度和加速度分别为
则初始时刻
可知初速度与加速度共线,物体运动的轨迹是一条直线,B符合题意,D不符合题意;
C.物体在y轴方向上加速度恒定且与速度同向,所以物体做匀加速直线运动,C不符合题意。
故答案为:B。
【分析】利用匀变速位移公式可以判别物体在分运动的速度情况;利用速度和加速度的合成可以判别物体的运动轨迹。
【答案】A
【解析】【解答】船参与了两个分运动,沿船头指向的分运动和顺水流而下的分运动,其中,合速度v合 方向 已知,大小未知,顺水流而下的分运动v水速度的大小和方向都已知,沿船头指向的分运动的速度v船大小和方向都未知,合速度与分速度遵循平行四边形定则(或三角形定则),如图
当 v合与 v船垂直时, v船最小,由几何关系得到 v船的最小值为v船
故答案为:A.
【分析】利用其速度的合成结合平行四边形定律可以求出最小的速度。
【答案】A
【解析】【解答】A.当船头与上游河岸成角,则有
此时小船的位移最小,最小位移为
A符合题意;
B.小船以最短时间过河,当静水速度与河岸垂直时,过河的时间最短,最短渡河时间为
沿河岸方向的位移
其合位移为
B不符合题意;
C.因为静水船速小于水流速度,则合速度方向不可能垂直于河岸,即小船过河的实际速度无法垂直于河岸,C不符合题意;
D.若小船过河的过程中水流速度大小是变化的,则水平方向是变速运动,加速度水平与初速度不共线,则小船运动轨迹为曲线,D不符合题意。
故答案为:A.
【分析】由于船速小于水速,当合速度垂直于船速时过河位移最小,利用速度的分解可以求出合速度的方向,结合几何关系可以求出最短的过河位移;利用船速垂直于河岸时过河时间最短,利用河岸宽度除以船速可以求出最短的过河时间;利用位移公式结合位移的合成可以求出合位移的大小;由于船速小于水速所以不能垂直于河岸过河;由于水流速度变化所以加速度与合速度不在同一直线上所以船做曲线运动。
【答案】B
【解析】【解答】将A物体的速度vA进行分解如图所示
则有vB=vAcosα
α减小,vA不变,则vB逐渐增大,说明B物体向上做加速运动,
故答案为:B。
【分析】考查速度的合成与分解问题。把物体A的速度沿着绳子的方向和垂直于绳子的方向进行分解。沿着绳子方向的分速度等于物体B的速度。根据三角函数关系判断物体B的运动情况。
【答案】C
【解析】【解答】由题意可知,玻璃管水平向右匀速运动,则移动的速度为: ;而在竖直方向的移动速度为: ;由速度的合成法则,则有红蜡块运动的合速度大小为: .
故答案为:C.
【分析】物体在两个方向上做匀速运动,结合运动的速度,利用勾股定理求解合速度即可。
【答案】C
【解析】【解答】AB.船运动的速度是沿绳子收缩方向的速度和绕定滑轮的摆动速度的合速度,根据平行四边形定则,有
AB不符合题意;
CD.对小船受力分析,则有
因此船的加速度大小为
C符合题意,D不符合题意。
故答案为:C。
【分析】对船的速度进行分解,利用平行四边形定则可以求出人速度的大小;利用船的牛顿第二定律可以求出船加速度的大小。
【答案】B
【解析】【解答】A.如图
把A的速度分解,沿绳方向的分速度与B的速度大小相等,关系式为
A不符合题意;
B.当时,A.B的速度大小之比是
B符合题意;
CD.当A环上升至与定滑轮的连线处于水平位置Q时,B的速度,由公式
可知当A上升时,夹角增大,因此B做向下的减速运动,加速度向上,由牛第二定律,可知绳对B的拉力大于B的重力,CD不符合题意。
故答案为:B。
【分析】对A的速度进行分解,利用沿绳子方向的速度相等可以求出B速度的大小,结合角度的大小可以求出AB速度之比;利用其夹角的变化可以判别B的速度大小变化,利用速度变化可以判别加速度的方向,进而比较拉力和重力的大小。
、多选题
【答案】A,C
【解析】【解答】A.时质点在x方向的初速度
在y方向的初速度
合速度
A符合题意;
B.在x方向的加速度大小为
质点的合力
B不符合题意;
C.质点在时间内速度的变化量大小为
C符合题意;
D.质点在x方向上做匀加速直线运动,在y方向上做匀速直线运动,所以质点做匀变速曲线运动,D不符合题意。
故答案为:AC。
【分析】利用其速度的合成可以求出初速度的大小;利用其图像斜率可以求出x方向的加速度大小,结合牛顿第二定律可以求出合力的大小;利用速度公式可以求出速度变化量的大小;利用其速度的方向和速度的方向可以判别质点做匀变速曲线运动。
【答案】B,D
【解析】【解答】根据题意可知,船在静水中的速度方向未知,所以,小船的合速度大小无法确定,故A错误;
当船头垂直于河岸时,小船渡河时间最短,最短时间为,船的合速度与河岸不垂直,所以实际运动轨迹与河岸不垂直,故B正确,C错误;
由于船在静水中的速度大于河水流速,所以想要轨迹最短需要合速度垂直河岸,作出图像可知,小船实际运动轨迹的最短位移是120 m,故D正确;
故选BD。
【分析】本题主要考查小船渡河问题,最短时间渡河需要船在静水中的速度与河岸垂直,最短位移需要小船的合速度与河岸垂直。
【答案】B,C
【解析】【解答】A.由图可知,质点在x轴做匀加速直线运动,初速度 ,加速度 ,在y轴做匀速直线运动,速度 ,故质点的初速度为
A不符合题意;
B.质点所受的合外力大小为
方向朝x轴正方向,B符合题意;
C.质点1秒末在两坐标上的分位移为
故合位移为
C符合题意;
D.质点初速度 在+x与+y间,合外力沿+x方向,故不垂直,D不符合题意。
故答案为:BC。
【分析】利用两个方向的初速度进行合成可以求出初速度的大小;利用y方向的图线斜率可以求出加速度的大小,结合牛顿第二定律可以求出合力的大小;利用两个方向位移进行合成可以求出合位移的大小;利用初速度的方向不在x方向可以判别与合力方向不垂直。
、解答题
【答案】(1)解:小车在A点时沿绳方向的分速度大小
物块的速度与小车沿绳方向的分速度相等
解得
(2)解:小车在A点时,斜面右侧绳的长度
小车在B点时,斜面右侧绳的长度
右侧绳的长度变化量
小车从A点运动到B点的时间
解得t=1s
【解析】【分析】(1)对小车的速度进行分解,利用分速度相同可以求出小车经过A点的速度大小;
(2)小车在A.B两点时,利用几何关系可以求出绳子长度的变化,利用物块的匀速运动的位移公式可以求出运动的时间。
【答案】(1)解:要使小船渡河时间最短,应使船头方向垂直对岸行驶,如图2所示.其渡河时间t= s=50 s.
(2)解:要使小船以最短路径渡河,合速度方向应垂直对岸,如图1所示.则 ,得θ=60°,即船头与河岸上游成60°角,这时v=v2sin θ=2 m/s
渡河时间:
【解析】【分析】(1)当船头垂直于河岸时过河时间最短,利用河岸宽度除以船在静水的速度可以求出最短的时间;
(2)当小球合速度方向垂直于河岸时其过河位移最短,利用速度的合成可以求出其船头的方向;结合速度合成可以求出合速度的大小,结合河岸宽度可以求出运动的时间。
第 1 页(共 1 页)
、单选题
关于两个运动的合成,下列说法正确的是( )
A.两个直线运动的合运动一定也是直线运动
B.方向不共线的两个匀速直线运动的合运动一定也是匀速直线运动
C.小船渡河的运动中,小船的对地速度一定大于水流速度
D.小船渡河的运动中,水流速度越大,小船渡河所需时间越短
小船以一定的速度垂直河岸向对岸航行时,下列说法正确的是( )
A.水流速度越大,小船运动的位移越长,时间不变
B.水流速度越大,小船运动的位移越长,时间越短
C.水流速度越大,小船运动的位移越长,时间越长
D.水流速度越大,小船运动的位移和时间都不变
一只小船在静水中的速度始终为 ,若在流速为 的河中航行,则站在河岸上的人看到船的实际航速可能是( )
A.
一物体在以xOy为直角坐标系的平面上运动,其运动规律为x=-2t2-4t,y=3t2+6t(式中的物理量单位均为国际单位),关于物体的运动,下列说法正确的是( )
A.物体在x轴方向上做匀减速直线运动
B.物体运动的轨迹是一条直线
C.物体在y轴方向上做变加速直线运动
D.物体运动的轨迹是一条曲线
如图所示,船从A处开出后沿直线到达对岸,若 A与河岸成30° 角,水流速度为4m/s ,则船从A点开出的最小速度为( )
A.2m/s B.2.4m/s C.3m/s D.3.5m/s
一条小船在静水中的速度为,它要渡过一条宽为的河,河水流速为,下列说法正确的是( )
A.小船过河的最短位移为
B.小船以最短时间过河,其位移为
C.小船过河的实际速度可以垂直于河岸
D.若小船在静水中的速度垂直河岸且保持不变,而水速的大小变化,则小船运动轨迹为直线
如图所示,物体A和B的质量均为m,分别与跨过定滑轮的轻绳连接(不计绳与滑轮、滑轮与轴之间的摩擦)。现用水平变力F拉着物体A沿水平方向向右做匀速直线运动。则下列说法中正确的是( )
A.物体B做匀速直线运动 B.物体B做加速直线运动
C.物体B做减速直线运动 D.无法判断
如图所示,有一长为80cm的玻璃管竖直放置,当红蜡块从玻璃管的最下端开始匀速上升的同时,玻璃管水平向右匀速运动.经过20s,红蜡块到达玻璃管的最上端,此过程玻璃管的水平位移为60cm.不计红蜡块的大小,则红蜡块运动的合速度大小为( )
A.3cm/s B.4cm/s C.5cm/s D.7cm/s
如图所示,人在岸上拉船,已知船的质量为m,水的阻力恒为f,当轻绳与水面的夹角为时,船的速度为v,人的拉力大小为F,则此时( )
A.人拉绳行走的速度为 B.人拉绳行走的速度为
C.船的加速度为 D.船的加速度为
如图所示,套在直细杆上的环A跨过定滑轮且不可伸长的轻绳与B相连,在外力作用下A沿杆以速度匀速上升经过P、Q两点,经过P点时绳与竖直杆间的角度为α,经过Q点时A与定滑轮的连线处于水平方向,则求( )
A.经过P点时,B的速度大小等于
B.当时A,B的速度大小之比是
C.在A从P至Q的过程中,B受到的拉力小于重力
D.经过Q点时,B的速度方向向下
、多选题
有一个质量为的质点在平面内运动,在x方向的速度-时间图像和y方向的位移-时间图像分别如图甲、乙所示。已知时质点在坐标原点上,关于该质点的运动,下列说法正确的是( )
A.时质点的速度大小为
B.质点所受的合外力大小为
C.质点在时间内速度的变化量大小为
D.质点的运动轨迹是一条直线
如图所示,一条小船过河,河宽d=120m,河水流速v1=3m/s,船在静水中速度v2=4m/s,关于小船的运动,以下说法正确的是( )
A.小船合运动的速度大小一定是5 m/s
B.小船渡河的最短时间为30 s
C.小船若以最短时间渡河,则其实际运动轨迹与河岸垂直
D.小船实际运动轨迹的最短位移是120 m
有一个质量为3kg的质点在xOy平面上运动,在x方向的速度图象和y方向的位移图象分别如图甲、乙所示,下列说法正确的是( )
A.质点的初速度为3m/s
B.质点所受的合外力为6N
C.质点1秒末的位移为 m
D.质点初速度的方向与合外力的方向垂直
、解答题
小物块置于倾角 =45°的固定光滑斜面靠近斜面底端的C点,轻细绳跨过光滑定滑轮分别连接着小物块与动力小车,滑轮到地面的距离h=4m,小物块与滑轮间的细绳平行于斜面,小车带动小物块使其以速度 m/s沿斜面向上做匀速直线运动,小车从A点到B点的过程中,连接小车的细绳与水平方向的夹角由 变化到 。已知sin53°=0.8,小物块和小车均可视为质点。求:
(1)小车在A点时的速度大小vA;
(2)小车从A点运动到B点的时间t。
一只船在200m宽的河中横渡,水流速度是2m/s,船在静水中的航速是4m/s,则
(1)小船怎样才能以最短时间渡过河去?需时多少?
(2)小船怎样才能以最短路径渡过河去 需时多少?
5.2运动的合成和分解答案解析
、单选题
【答案】B
【解析】【解答】两个分运动是直线运动,其合运动可能是曲线运动,比如平抛运动.A不符合题意.不共线两个匀速直线运动,没有加速度,则合运动也一定是匀速直线运动.B符合题意.合运动的速度(小船对地速度)可能比分速度(水流速度)大,可能比分速度小,可能与分速度相等.C不符合题意;小船渡河的时间由小船沿垂直于河岸方向的速度决定,故水流速度越大,小船渡河所需时间却不变,D不符合题意.
故答案为:B.
【分析】位移、速度、加速度都是矢量,合成分解遵循平行四边形定则.合运动与分运动具有等时性.
【答案】A
【解析】【解答】设河宽为d,船垂直于河岸的速度为v,河流的速度为v1
时间与水速无关;合速度为
运动位移
其中t不变,v不变,则河流的速度v1越大,位移越长;
故答案为:A.
【分析】当船头垂直于河岸时,渡河时间最短,与水流速度无关,利用速度的合成以及匀速直线运动的规律得出河流速度和位移的关系。
【答案】B
【解析】【解答】由平行四边形定则可得出其合速度的范围是大于或等于2m/s小于或等于8m/s,其间的任一速度值都有可能,则B符合题意,ACD不在其范围之内错误。
故答案为:B。
【分析】速度的合成遵循平行四边形定则,已知两个速度的大小和方向,利用平行四边形定则求解合速度即可。
【答案】B
【解析】【解答】A.根据匀变速直线运动的规律 可知 方向初速度和加速度分别为
速度与加速度同向,物体在x轴方向上做匀加速直线运动,A不符合题意;
B. 方向初速度和加速度分别为
则初始时刻
可知初速度与加速度共线,物体运动的轨迹是一条直线,B符合题意,D不符合题意;
C.物体在y轴方向上加速度恒定且与速度同向,所以物体做匀加速直线运动,C不符合题意。
故答案为:B。
【分析】利用匀变速位移公式可以判别物体在分运动的速度情况;利用速度和加速度的合成可以判别物体的运动轨迹。
【答案】A
【解析】【解答】船参与了两个分运动,沿船头指向的分运动和顺水流而下的分运动,其中,合速度v合 方向 已知,大小未知,顺水流而下的分运动v水速度的大小和方向都已知,沿船头指向的分运动的速度v船大小和方向都未知,合速度与分速度遵循平行四边形定则(或三角形定则),如图
当 v合与 v船垂直时, v船最小,由几何关系得到 v船的最小值为v船
故答案为:A.
【分析】利用其速度的合成结合平行四边形定律可以求出最小的速度。
【答案】A
【解析】【解答】A.当船头与上游河岸成角,则有
此时小船的位移最小,最小位移为
A符合题意;
B.小船以最短时间过河,当静水速度与河岸垂直时,过河的时间最短,最短渡河时间为
沿河岸方向的位移
其合位移为
B不符合题意;
C.因为静水船速小于水流速度,则合速度方向不可能垂直于河岸,即小船过河的实际速度无法垂直于河岸,C不符合题意;
D.若小船过河的过程中水流速度大小是变化的,则水平方向是变速运动,加速度水平与初速度不共线,则小船运动轨迹为曲线,D不符合题意。
故答案为:A.
【分析】由于船速小于水速,当合速度垂直于船速时过河位移最小,利用速度的分解可以求出合速度的方向,结合几何关系可以求出最短的过河位移;利用船速垂直于河岸时过河时间最短,利用河岸宽度除以船速可以求出最短的过河时间;利用位移公式结合位移的合成可以求出合位移的大小;由于船速小于水速所以不能垂直于河岸过河;由于水流速度变化所以加速度与合速度不在同一直线上所以船做曲线运动。
【答案】B
【解析】【解答】将A物体的速度vA进行分解如图所示
则有vB=vAcosα
α减小,vA不变,则vB逐渐增大,说明B物体向上做加速运动,
故答案为:B。
【分析】考查速度的合成与分解问题。把物体A的速度沿着绳子的方向和垂直于绳子的方向进行分解。沿着绳子方向的分速度等于物体B的速度。根据三角函数关系判断物体B的运动情况。
【答案】C
【解析】【解答】由题意可知,玻璃管水平向右匀速运动,则移动的速度为: ;而在竖直方向的移动速度为: ;由速度的合成法则,则有红蜡块运动的合速度大小为: .
故答案为:C.
【分析】物体在两个方向上做匀速运动,结合运动的速度,利用勾股定理求解合速度即可。
【答案】C
【解析】【解答】AB.船运动的速度是沿绳子收缩方向的速度和绕定滑轮的摆动速度的合速度,根据平行四边形定则,有
AB不符合题意;
CD.对小船受力分析,则有
因此船的加速度大小为
C符合题意,D不符合题意。
故答案为:C。
【分析】对船的速度进行分解,利用平行四边形定则可以求出人速度的大小;利用船的牛顿第二定律可以求出船加速度的大小。
【答案】B
【解析】【解答】A.如图
把A的速度分解,沿绳方向的分速度与B的速度大小相等,关系式为
A不符合题意;
B.当时,A.B的速度大小之比是
B符合题意;
CD.当A环上升至与定滑轮的连线处于水平位置Q时,B的速度,由公式
可知当A上升时,夹角增大,因此B做向下的减速运动,加速度向上,由牛第二定律,可知绳对B的拉力大于B的重力,CD不符合题意。
故答案为:B。
【分析】对A的速度进行分解,利用沿绳子方向的速度相等可以求出B速度的大小,结合角度的大小可以求出AB速度之比;利用其夹角的变化可以判别B的速度大小变化,利用速度变化可以判别加速度的方向,进而比较拉力和重力的大小。
、多选题
【答案】A,C
【解析】【解答】A.时质点在x方向的初速度
在y方向的初速度
合速度
A符合题意;
B.在x方向的加速度大小为
质点的合力
B不符合题意;
C.质点在时间内速度的变化量大小为
C符合题意;
D.质点在x方向上做匀加速直线运动,在y方向上做匀速直线运动,所以质点做匀变速曲线运动,D不符合题意。
故答案为:AC。
【分析】利用其速度的合成可以求出初速度的大小;利用其图像斜率可以求出x方向的加速度大小,结合牛顿第二定律可以求出合力的大小;利用速度公式可以求出速度变化量的大小;利用其速度的方向和速度的方向可以判别质点做匀变速曲线运动。
【答案】B,D
【解析】【解答】根据题意可知,船在静水中的速度方向未知,所以,小船的合速度大小无法确定,故A错误;
当船头垂直于河岸时,小船渡河时间最短,最短时间为,船的合速度与河岸不垂直,所以实际运动轨迹与河岸不垂直,故B正确,C错误;
由于船在静水中的速度大于河水流速,所以想要轨迹最短需要合速度垂直河岸,作出图像可知,小船实际运动轨迹的最短位移是120 m,故D正确;
故选BD。
【分析】本题主要考查小船渡河问题,最短时间渡河需要船在静水中的速度与河岸垂直,最短位移需要小船的合速度与河岸垂直。
【答案】B,C
【解析】【解答】A.由图可知,质点在x轴做匀加速直线运动,初速度 ,加速度 ,在y轴做匀速直线运动,速度 ,故质点的初速度为
A不符合题意;
B.质点所受的合外力大小为
方向朝x轴正方向,B符合题意;
C.质点1秒末在两坐标上的分位移为
故合位移为
C符合题意;
D.质点初速度 在+x与+y间,合外力沿+x方向,故不垂直,D不符合题意。
故答案为:BC。
【分析】利用两个方向的初速度进行合成可以求出初速度的大小;利用y方向的图线斜率可以求出加速度的大小,结合牛顿第二定律可以求出合力的大小;利用两个方向位移进行合成可以求出合位移的大小;利用初速度的方向不在x方向可以判别与合力方向不垂直。
、解答题
【答案】(1)解:小车在A点时沿绳方向的分速度大小
物块的速度与小车沿绳方向的分速度相等
解得
(2)解:小车在A点时,斜面右侧绳的长度
小车在B点时,斜面右侧绳的长度
右侧绳的长度变化量
小车从A点运动到B点的时间
解得t=1s
【解析】【分析】(1)对小车的速度进行分解,利用分速度相同可以求出小车经过A点的速度大小;
(2)小车在A.B两点时,利用几何关系可以求出绳子长度的变化,利用物块的匀速运动的位移公式可以求出运动的时间。
【答案】(1)解:要使小船渡河时间最短,应使船头方向垂直对岸行驶,如图2所示.其渡河时间t= s=50 s.
(2)解:要使小船以最短路径渡河,合速度方向应垂直对岸,如图1所示.则 ,得θ=60°,即船头与河岸上游成60°角,这时v=v2sin θ=2 m/s
渡河时间:
【解析】【分析】(1)当船头垂直于河岸时过河时间最短,利用河岸宽度除以船在静水的速度可以求出最短的时间;
(2)当小球合速度方向垂直于河岸时其过河位移最短,利用速度的合成可以求出其船头的方向;结合速度合成可以求出合速度的大小,结合河岸宽度可以求出运动的时间。
第 1 页(共 1 页)
