高二数学人教A版(2019)选择性必修第一册 2.1.1 倾斜角与斜率 教案
文档属性
| 名称 | 高二数学人教A版(2019)选择性必修第一册 2.1.1 倾斜角与斜率 教案 |

|
|
| 格式 | docx | ||
| 文件大小 | 808.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-24 00:00:00 | ||
图片预览

文档简介
第二章 直线和圆的方程
2.1 直线的倾斜角与斜率
2.1.1 倾斜角与斜率
一、教学目标
1、正确理解直线的倾斜角和斜率的概念.
2、正确理解斜率公式的推导过程,掌握过两点的直线的斜率公式.
3、学会将直线的位置问题(几何问题)转化为倾斜角问题,进而转化为倾斜角的正切即斜率问题(代数问题)进行解决,使学生不断体会“数形结合”的思想方法.
4、通过斜率概念的建立和斜率公式的推导,帮助学生进一步理解数形结合的思想,培养学生树立辩证统一的观点,培养学生形成严谨的科学态度和求简的数学精神.
二、教学重点、难点
重点:直线的倾斜角的概念、直线的斜率概念
难点:直线的倾斜角与斜率的范围问题
三、学法与教学用具
1、学法:学生在老师的引导下,通过阅读教材,自主学习、思考、交流、讨论和概括,从而完成本节课的教学目标.
2、教学用具:多媒体设备等
四、教学过程
(一)创设情景,揭示课题
【观看视频】世界第一高桥-北盘江大桥.
【问题】如何描述大桥的斜拉钢丝所表示的直线与桥面的关系?
布置学生阅读课本~ (预定用时3-4分钟)
(二)阅读精要,研讨新知
【内容简述】
【直线的倾斜角】
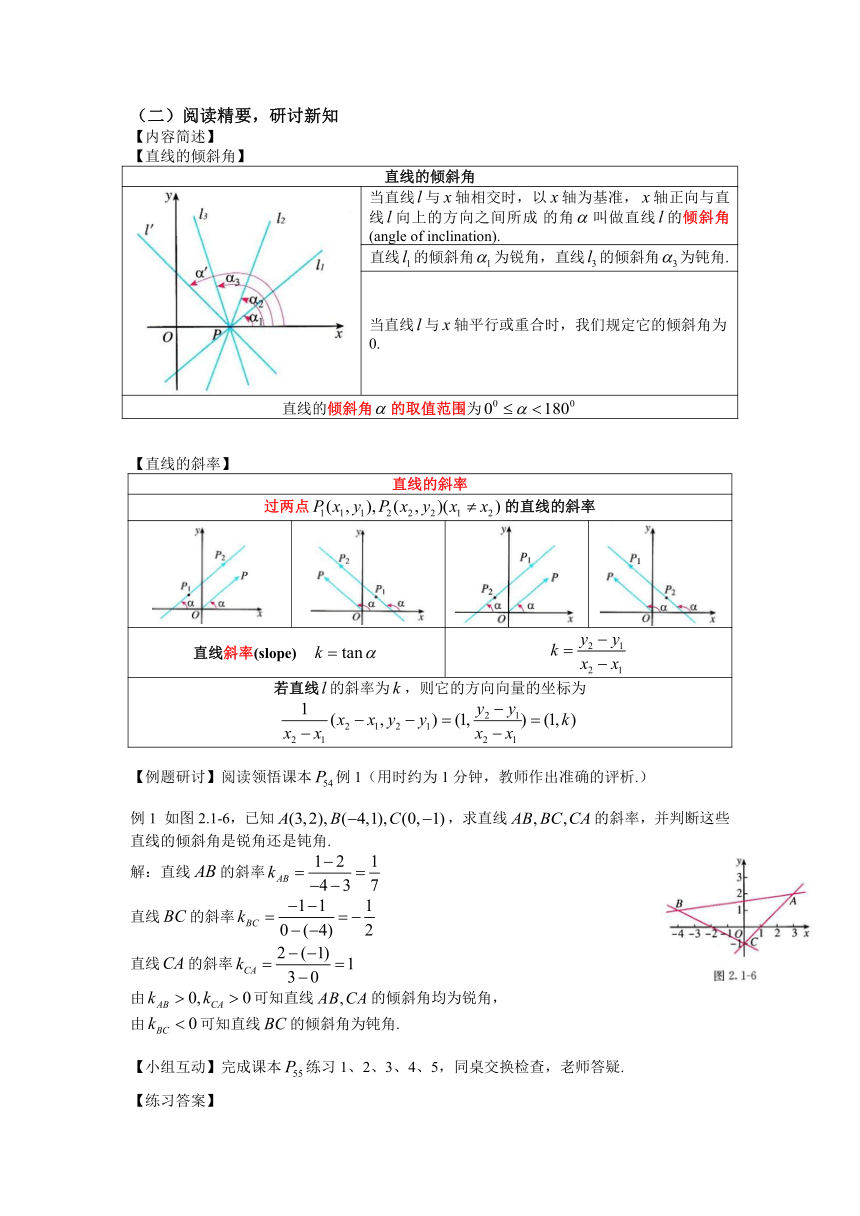
直线的倾斜角
当直线与轴相交时,以轴为基准,轴正向与直线向上的方向之间所成 的角叫做直线的倾斜角(angle of inclination).
直线的倾斜角为锐角,直线的倾斜角为钝角.
当直线与轴平行或重合时,我们规定它的倾斜角为0.
直线的倾斜角的取值范围为
【直线的斜率】
直线的斜率
过两点的直线的斜率
直线斜率(slope)
若直线的斜率为,则它的方向向量的坐标为
【例题研讨】阅读领悟课本例1(用时约为1分钟,教师作出准确的评析.)
例1 如图2.1-6,已知,求直线的斜率,并判断这些直线的倾斜角是锐角还是钝角.
解:直线的斜率
直线的斜率
直线的斜率
由可知直线的倾斜角均为锐角,
由可知直线的倾斜角为钝角.
【小组互动】完成课本练习1、2、3、4、5,同桌交换检查,老师答疑.
【练习答案】
(三)探索与发现、思考与感悟
1.(多选)下列结论中,正确的是( )
A. 若直线过点,则直线的倾斜角是
B. 过点的直线的倾斜角等于,则
C. 若直线过两点,则直线斜率的取值范围是
D. 经过的直线的方向向量为,则
解:对于A,,所以,正确;
对于B,,解得,错误;
对于C,,所以,正确;
对于D ,,正确,故选ABD
2. 直线的斜率为,倾斜角是,若,则的取值范围是________.
解:由已知,结合正切函数图象,可知的取值范围是.
答案:
3. 若直线的倾斜角为满足则此直线的斜率为( )
A.或 B.或 C. D.
解:由得
又所以是方程的两根,
所以
又,所以,所以,即,故选C
4. 已知函数,则的大小关系是 .
解:可视为过原点和点的直线的斜率,作图分析,
观察图形可知,,
答案:
(四)归纳小结,回顾重点
直线的倾斜角
轴正向与直线向上的方向所成的角叫做直线的倾斜角(angle of inclination).
直线的倾斜角 及其分类
斜率分类 不存在
直线的斜率的两种方式
过两点的直线的斜率为
直线斜率(slope)
直线的方向向量的坐标为
(五)作业布置,精炼双基
1.完成课本习题2.1 1、2、3、7
2.预习2.1.2 两条直线平行和垂直的判定
五、教学反思:(课后补充,教学相长)
2.1 直线的倾斜角与斜率
2.1.1 倾斜角与斜率
一、教学目标
1、正确理解直线的倾斜角和斜率的概念.
2、正确理解斜率公式的推导过程,掌握过两点的直线的斜率公式.
3、学会将直线的位置问题(几何问题)转化为倾斜角问题,进而转化为倾斜角的正切即斜率问题(代数问题)进行解决,使学生不断体会“数形结合”的思想方法.
4、通过斜率概念的建立和斜率公式的推导,帮助学生进一步理解数形结合的思想,培养学生树立辩证统一的观点,培养学生形成严谨的科学态度和求简的数学精神.
二、教学重点、难点
重点:直线的倾斜角的概念、直线的斜率概念
难点:直线的倾斜角与斜率的范围问题
三、学法与教学用具
1、学法:学生在老师的引导下,通过阅读教材,自主学习、思考、交流、讨论和概括,从而完成本节课的教学目标.
2、教学用具:多媒体设备等
四、教学过程
(一)创设情景,揭示课题
【观看视频】世界第一高桥-北盘江大桥.
【问题】如何描述大桥的斜拉钢丝所表示的直线与桥面的关系?
布置学生阅读课本~ (预定用时3-4分钟)
(二)阅读精要,研讨新知
【内容简述】
【直线的倾斜角】
直线的倾斜角
当直线与轴相交时,以轴为基准,轴正向与直线向上的方向之间所成 的角叫做直线的倾斜角(angle of inclination).
直线的倾斜角为锐角,直线的倾斜角为钝角.
当直线与轴平行或重合时,我们规定它的倾斜角为0.
直线的倾斜角的取值范围为
【直线的斜率】
直线的斜率
过两点的直线的斜率
直线斜率(slope)
若直线的斜率为,则它的方向向量的坐标为
【例题研讨】阅读领悟课本例1(用时约为1分钟,教师作出准确的评析.)
例1 如图2.1-6,已知,求直线的斜率,并判断这些直线的倾斜角是锐角还是钝角.
解:直线的斜率
直线的斜率
直线的斜率
由可知直线的倾斜角均为锐角,
由可知直线的倾斜角为钝角.
【小组互动】完成课本练习1、2、3、4、5,同桌交换检查,老师答疑.
【练习答案】
(三)探索与发现、思考与感悟
1.(多选)下列结论中,正确的是( )
A. 若直线过点,则直线的倾斜角是
B. 过点的直线的倾斜角等于,则
C. 若直线过两点,则直线斜率的取值范围是
D. 经过的直线的方向向量为,则
解:对于A,,所以,正确;
对于B,,解得,错误;
对于C,,所以,正确;
对于D ,,正确,故选ABD
2. 直线的斜率为,倾斜角是,若,则的取值范围是________.
解:由已知,结合正切函数图象,可知的取值范围是.
答案:
3. 若直线的倾斜角为满足则此直线的斜率为( )
A.或 B.或 C. D.
解:由得
又所以是方程的两根,
所以
又,所以,所以,即,故选C
4. 已知函数,则的大小关系是 .
解:可视为过原点和点的直线的斜率,作图分析,
观察图形可知,,
答案:
(四)归纳小结,回顾重点
直线的倾斜角
轴正向与直线向上的方向所成的角叫做直线的倾斜角(angle of inclination).
直线的倾斜角 及其分类
斜率分类 不存在
直线的斜率的两种方式
过两点的直线的斜率为
直线斜率(slope)
直线的方向向量的坐标为
(五)作业布置,精炼双基
1.完成课本习题2.1 1、2、3、7
2.预习2.1.2 两条直线平行和垂直的判定
五、教学反思:(课后补充,教学相长)
