高二数学人教A版(2019)选择性必修第一册 2.1.2 两条直线平行和垂直的判定 教案
文档属性
| 名称 | 高二数学人教A版(2019)选择性必修第一册 2.1.2 两条直线平行和垂直的判定 教案 |

|
|
| 格式 | docx | ||
| 文件大小 | 558.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-24 00:00:00 | ||
图片预览

文档简介
第二章 直线和圆的方程
2.1 直线的倾斜角与斜率
2.1.2 两条直线平行和垂直的判定
一、教学目标
1、理解并掌握两条直线平行与垂直的条件,会运用条件判定两直线是否平行或垂直.
2、通过探究两直线平行或垂直的条件,培养学生运用正确知识解决新问题的能力,以及数形结合能力.
3、通过对两直线平行与垂直的位置关系的研究,培养学生的成功意识,合作交流的学习方式,激发学生的学习兴趣.
二、教学重点、难点
重点:两条直线平行和垂直的条件.
难点:启发学生,把研究两条直线的平行或垂直问题,转化为研究两条直线的斜率的关系问题.
三、学法与教学用具
1、学法:学生在老师的引导下,通过阅读教材,自主学习、思考、交流、讨论和概括,从而完成本节课的教学目标.
2、教学用具:多媒体设备等
四、教学过程
(一)创设情景,揭示课题
【实例】在许多地方,都能看见两条直线平行或垂直的现象
(1)建筑中的直线平行与垂直的关系
(2)桥梁建设中斜拉桥中的直线的平行与垂直的关系
【问题】上一节课已经利用直线的倾斜角和斜率描述直线,能否用直线的倾斜角和斜率描述两条直线平行和垂直的关系?
(二)阅读精要,研讨新知
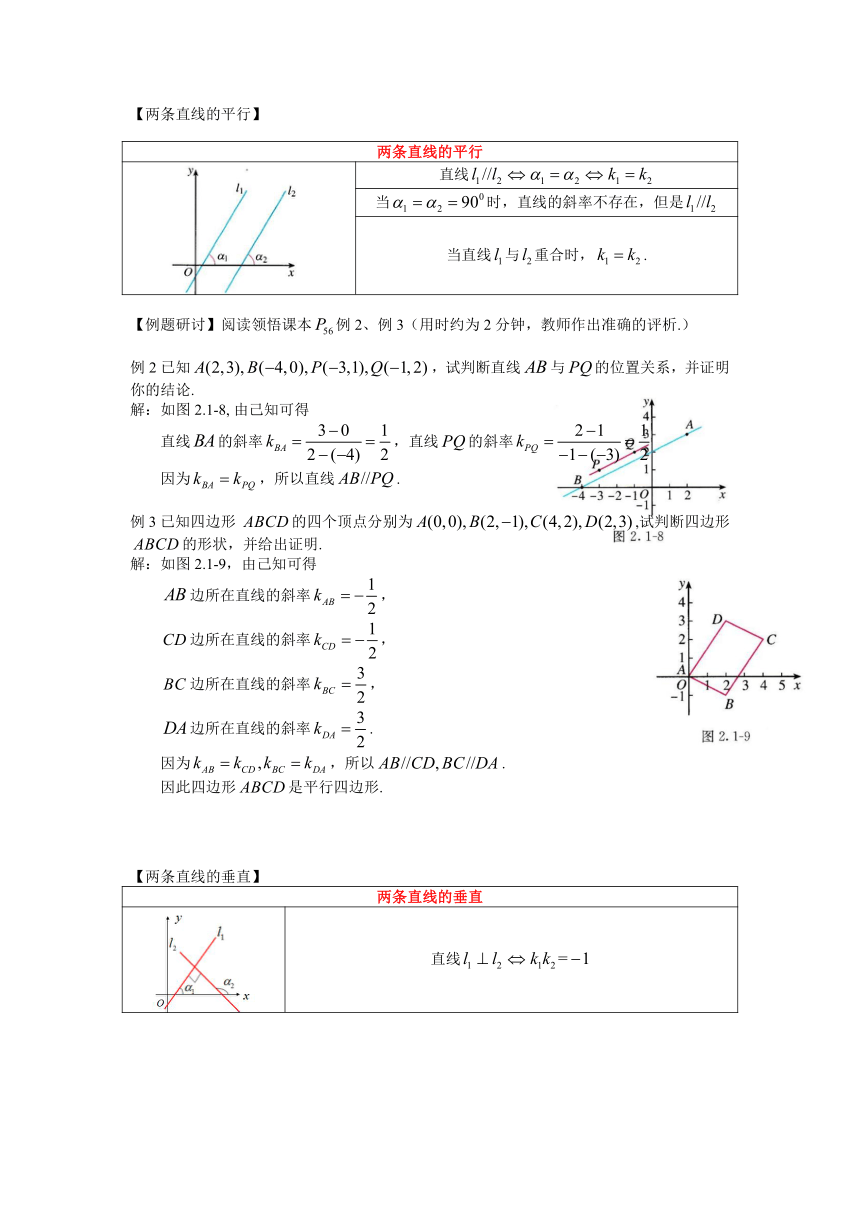
【两条直线的平行】
两条直线的平行
直线
当时,直线的斜率不存在,但是
当直线与重合时,.
【例题研讨】阅读领悟课本例2、例3(用时约为2分钟,教师作出准确的评析.)
例2已知,试判断直线与的位置关系,并证明你的结论.
解:如图2.1-8, 由己知可得
直线的斜率,直线的斜率
因为,所以直线.
例3已知四边形 的四个顶点分别为,试判断四边形的形状,并给出证明.
解:如图2.1-9,由己知可得
边所在直线的斜率,
边所在直线的斜率,
边所在直线的斜率,
边所在直线的斜率.
因为,所以.
因此四边形是平行四边形.
【两条直线的垂直】
两条直线的垂直
直线
两条直线的斜率,的斜率不存在,成立
【例题研讨】阅读领悟课本例4、例5(用时约为2分钟,教师作出准确的评析.)
例4已知, 试判断直线与的位置关系.
解:直线的斜率,直线的斜率
因为,所以直线.
例5已知三点,试判断的形状.
解:边所在直线的斜率,边所在直线的斜率.
由,得,即;
所以是直角三角形.
【小组互动】完成课本练习1、2,同桌交换检查,老师答疑.
【练习答案】
(三)探索与发现、思考与感悟
1.(多选)下列结论中,正确的是( )
A. 已知直线的倾斜角为,直线的斜率,若,则
B. 直线满足,若直线的倾斜角为,则直线的斜率为
C. 过点的直线与直线平行
D. 已知,则四边形为矩形
解:对于A,因为,所以,解得,A错;
对于B,,正确;
对于C,,所以直线与直线平行,正确;
对于D,,所以,所以四边形为平行四边形,
又,所以,所以四边形为矩形,正确,故选BCD
2. 已知两平行直线的斜率是方程的两实根,则的值为 ( )
A. B. C. D.
解:由题意知方程的两实根相等,
所以,故选C.
3. 以为顶点的三角形是( )
A.锐角三角形 B.钝角三角形
C.以为直角顶点的直角三角形 D.以为直角顶点的直角三角形
解: 所以,所以,即,
因此是以为直角顶点的直角三角形,故选D.
(四)归纳小结,回顾重点
两条直线的平行
直线
当时,直线的斜率不存在,但是
当直线与重合时,.
两条直线的垂直
直线
两条直线的斜率,的斜率不存在,成立
(五)作业布置,精炼双基
1.完成课本习题2.1 4、5、6、8、9、10
2.预习2.2 直线的方程
五、教学反思:(课后补充,教学相长)
2.1 直线的倾斜角与斜率
2.1.2 两条直线平行和垂直的判定
一、教学目标
1、理解并掌握两条直线平行与垂直的条件,会运用条件判定两直线是否平行或垂直.
2、通过探究两直线平行或垂直的条件,培养学生运用正确知识解决新问题的能力,以及数形结合能力.
3、通过对两直线平行与垂直的位置关系的研究,培养学生的成功意识,合作交流的学习方式,激发学生的学习兴趣.
二、教学重点、难点
重点:两条直线平行和垂直的条件.
难点:启发学生,把研究两条直线的平行或垂直问题,转化为研究两条直线的斜率的关系问题.
三、学法与教学用具
1、学法:学生在老师的引导下,通过阅读教材,自主学习、思考、交流、讨论和概括,从而完成本节课的教学目标.
2、教学用具:多媒体设备等
四、教学过程
(一)创设情景,揭示课题
【实例】在许多地方,都能看见两条直线平行或垂直的现象
(1)建筑中的直线平行与垂直的关系
(2)桥梁建设中斜拉桥中的直线的平行与垂直的关系
【问题】上一节课已经利用直线的倾斜角和斜率描述直线,能否用直线的倾斜角和斜率描述两条直线平行和垂直的关系?
(二)阅读精要,研讨新知
【两条直线的平行】
两条直线的平行
直线
当时,直线的斜率不存在,但是
当直线与重合时,.
【例题研讨】阅读领悟课本例2、例3(用时约为2分钟,教师作出准确的评析.)
例2已知,试判断直线与的位置关系,并证明你的结论.
解:如图2.1-8, 由己知可得
直线的斜率,直线的斜率
因为,所以直线.
例3已知四边形 的四个顶点分别为,试判断四边形的形状,并给出证明.
解:如图2.1-9,由己知可得
边所在直线的斜率,
边所在直线的斜率,
边所在直线的斜率,
边所在直线的斜率.
因为,所以.
因此四边形是平行四边形.
【两条直线的垂直】
两条直线的垂直
直线
两条直线的斜率,的斜率不存在,成立
【例题研讨】阅读领悟课本例4、例5(用时约为2分钟,教师作出准确的评析.)
例4已知, 试判断直线与的位置关系.
解:直线的斜率,直线的斜率
因为,所以直线.
例5已知三点,试判断的形状.
解:边所在直线的斜率,边所在直线的斜率.
由,得,即;
所以是直角三角形.
【小组互动】完成课本练习1、2,同桌交换检查,老师答疑.
【练习答案】
(三)探索与发现、思考与感悟
1.(多选)下列结论中,正确的是( )
A. 已知直线的倾斜角为,直线的斜率,若,则
B. 直线满足,若直线的倾斜角为,则直线的斜率为
C. 过点的直线与直线平行
D. 已知,则四边形为矩形
解:对于A,因为,所以,解得,A错;
对于B,,正确;
对于C,,所以直线与直线平行,正确;
对于D,,所以,所以四边形为平行四边形,
又,所以,所以四边形为矩形,正确,故选BCD
2. 已知两平行直线的斜率是方程的两实根,则的值为 ( )
A. B. C. D.
解:由题意知方程的两实根相等,
所以,故选C.
3. 以为顶点的三角形是( )
A.锐角三角形 B.钝角三角形
C.以为直角顶点的直角三角形 D.以为直角顶点的直角三角形
解: 所以,所以,即,
因此是以为直角顶点的直角三角形,故选D.
(四)归纳小结,回顾重点
两条直线的平行
直线
当时,直线的斜率不存在,但是
当直线与重合时,.
两条直线的垂直
直线
两条直线的斜率,的斜率不存在,成立
(五)作业布置,精炼双基
1.完成课本习题2.1 4、5、6、8、9、10
2.预习2.2 直线的方程
五、教学反思:(课后补充,教学相长)
