高二数学人教A版(2019)选择性必修第一册 3.2.1 双曲线及其标准方程 教案
文档属性
| 名称 | 高二数学人教A版(2019)选择性必修第一册 3.2.1 双曲线及其标准方程 教案 |

|
|
| 格式 | docx | ||
| 文件大小 | 774.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-24 00:00:00 | ||
图片预览


文档简介
第三章 圆锥曲线的方程
3.2 双曲线
3.2.1 双曲线及其标准方程
一、教学目标
1、了解双曲线的实际背景,感受双曲线在刻画现实世界和解决实际问题中的作用.
2、掌握双曲线的定义,会求双曲线的标准方程.
二、教学重点、难点
重点: 对双曲线的定义的准确掌握,双曲线的两种形式的标准方程
难点: 双曲线定义的应用、求各种条件下的双曲线标准方程
三、学法与教学用具
1、学法:学生在老师的引导下,通过阅读教材,自主学习、思考、交流、讨论和概括,从而完成本节课的教学目标.
2、教学用具:多媒体设备等
四、教学过程
(一)创设情景,揭示课题
【情景一】与双曲线有关的物体
【情景二】生活中的双曲线
【问题】如何对双曲线进行有效快速的认知?与之前的椭圆学习有什么关联?
(二)阅读精要,研讨新知
【类比】
椭圆的定义
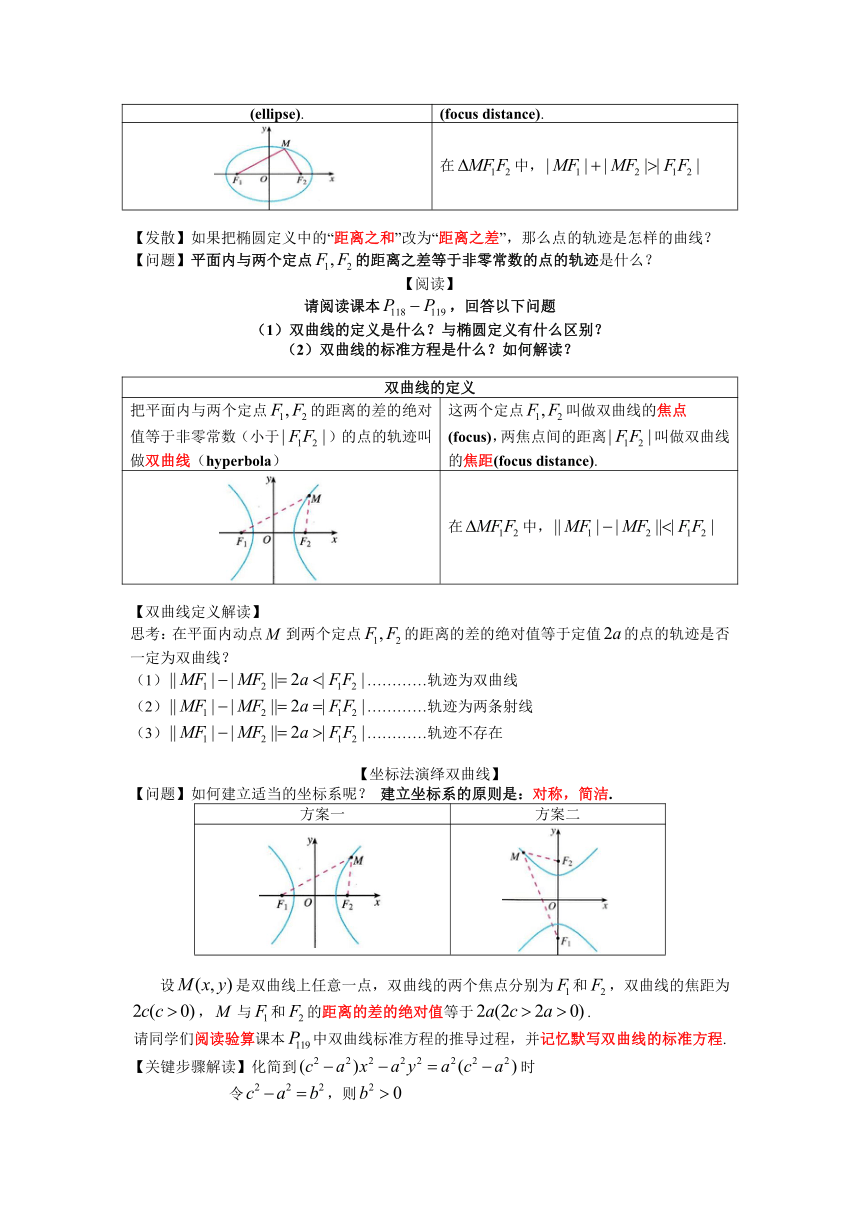
把平面内与两个定点的距离的和等于常数(大于)的点的轨迹叫做椭圆(ellipse). 这两个定点叫做椭圆的焦点(focus),两焦点间的距离叫做椭圆的焦距(focus distance).
在中,
【发散】如果把椭圆定义中的“距离之和”改为“距离之差”,那么点的轨迹是怎样的曲线?
【问题】平面内与两个定点的距离之差等于非零常数的点的轨迹是什么?
【阅读】
请阅读课本,回答以下问题
(1)双曲线的定义是什么?与椭圆定义有什么区别?
(2)双曲线的标准方程是什么?如何解读?
双曲线的定义
把平面内与两个定点的距离的差的绝对值等于非零常数(小于)的点的轨迹叫做双曲线(hyperbola) 这两个定点叫做双曲线的焦点(focus),两焦点间的距离叫做双曲线的焦距(focus distance).
在中,
【双曲线定义解读】
思考:在平面内动点到两个定点的距离的差的绝对值等于定值的点的轨迹是否一定为双曲线?
(1)…………轨迹为双曲线
(2)…………轨迹为两条射线
(3)…………轨迹不存在
【坐标法演绎双曲线】
【问题】如何建立适当的坐标系呢? 建立坐标系的原则是:对称,简洁.
方案一 方案二
设是双曲线上任意一点,双曲线的两个焦点分别为和,双曲线的焦距为,与和的距离的差的绝对值等于.
请同学们阅读验算课本中双曲线标准方程的推导过程,并记忆默写双曲线的标准方程.
【关键步骤解读】化简到时
令,则
所以,即
【双曲线标准方程认知】
焦点位置 标准方程 焦点 焦距 系数关系
焦点在轴上
焦点在轴上
【例题研讨】阅读领悟课本例1、例2(用时约为2-3分钟,教师作出准确的评析.)
例1 已知双曲线的两个焦点分别为, 双曲线上一点与的距离差的绝对值等于6,求双曲线的标准方程.
解:由已知,双曲线的焦点在轴上,且,
又,所以,从而,
所以双曲线的标准方程为
例2已知两地相距800 m,在地听到炮弹爆炸声比在地晚2 s,且声速 为340 m/s,求炮弹爆炸点的轨迹方程.
解:如图3.2-5,建立平面直角坐标系,使两点在轴上,
并且原点与线段的中点重合.
设炮弹爆炸点为,则,
即
又所以, 44 400.
因为,所以点的轨迹是双曲线的右支,因此.
所以,炮弹爆炸点的轨迹方程为
【小组互动】完成课本练习1、2、3、4,同桌交换检查,老师答疑.
【练习答案】
(三)探索与发现、思考与感悟
类型一 双曲线的定义及其应用
1.若双曲线的左、右焦点分别为,点在双曲线上,且则( )
A.11 B.9 C.5 D.3
解:由双曲线的定义,得,即解得 (负值舍去).故选B.
2.设分别是双曲线的左、右焦点,是双曲线上的一点,且,则的面积等于( )
A. B. C.24 D.48
解:由题意得,解得,又,可得为直角三角形,
所以,故选C.
类型二 双曲线标准方程的求法及应用
3. 方程表示双曲线,则的取值范围是( )
A. B. C. D.
解:由双曲线的标准方程,可知
即,故选A.
4. 焦距为,且经过点的双曲线的标准方程为( )
A. B. C. D.
解:因为双曲线经过点,所以为双曲线的一个顶点,故焦点在轴上,且
又,所以双曲线的标准方程为,故选B
5.双曲线上两点的坐标分别为,则此双曲线的标准方程为___________.
解:设双曲线的方程为,则,解得
所以双曲线的标准方程为
答案:
(四)归纳小结,回顾重点
椭圆 双曲线
定 义
标准方程 焦点在轴上, 焦点在轴上, 焦点在轴上, 焦点在轴上,
焦 点 , ,
的关系 ,未必有
(五)作业布置,精炼双基
1.完成课本习题3.2 1、2、5、7、9、10
2.预习3.2.2 双曲线的简单的几何性质
五、教学反思:(课后补充,教学相长)
3.2 双曲线
3.2.1 双曲线及其标准方程
一、教学目标
1、了解双曲线的实际背景,感受双曲线在刻画现实世界和解决实际问题中的作用.
2、掌握双曲线的定义,会求双曲线的标准方程.
二、教学重点、难点
重点: 对双曲线的定义的准确掌握,双曲线的两种形式的标准方程
难点: 双曲线定义的应用、求各种条件下的双曲线标准方程
三、学法与教学用具
1、学法:学生在老师的引导下,通过阅读教材,自主学习、思考、交流、讨论和概括,从而完成本节课的教学目标.
2、教学用具:多媒体设备等
四、教学过程
(一)创设情景,揭示课题
【情景一】与双曲线有关的物体
【情景二】生活中的双曲线
【问题】如何对双曲线进行有效快速的认知?与之前的椭圆学习有什么关联?
(二)阅读精要,研讨新知
【类比】
椭圆的定义
把平面内与两个定点的距离的和等于常数(大于)的点的轨迹叫做椭圆(ellipse). 这两个定点叫做椭圆的焦点(focus),两焦点间的距离叫做椭圆的焦距(focus distance).
在中,
【发散】如果把椭圆定义中的“距离之和”改为“距离之差”,那么点的轨迹是怎样的曲线?
【问题】平面内与两个定点的距离之差等于非零常数的点的轨迹是什么?
【阅读】
请阅读课本,回答以下问题
(1)双曲线的定义是什么?与椭圆定义有什么区别?
(2)双曲线的标准方程是什么?如何解读?
双曲线的定义
把平面内与两个定点的距离的差的绝对值等于非零常数(小于)的点的轨迹叫做双曲线(hyperbola) 这两个定点叫做双曲线的焦点(focus),两焦点间的距离叫做双曲线的焦距(focus distance).
在中,
【双曲线定义解读】
思考:在平面内动点到两个定点的距离的差的绝对值等于定值的点的轨迹是否一定为双曲线?
(1)…………轨迹为双曲线
(2)…………轨迹为两条射线
(3)…………轨迹不存在
【坐标法演绎双曲线】
【问题】如何建立适当的坐标系呢? 建立坐标系的原则是:对称,简洁.
方案一 方案二
设是双曲线上任意一点,双曲线的两个焦点分别为和,双曲线的焦距为,与和的距离的差的绝对值等于.
请同学们阅读验算课本中双曲线标准方程的推导过程,并记忆默写双曲线的标准方程.
【关键步骤解读】化简到时
令,则
所以,即
【双曲线标准方程认知】
焦点位置 标准方程 焦点 焦距 系数关系
焦点在轴上
焦点在轴上
【例题研讨】阅读领悟课本例1、例2(用时约为2-3分钟,教师作出准确的评析.)
例1 已知双曲线的两个焦点分别为, 双曲线上一点与的距离差的绝对值等于6,求双曲线的标准方程.
解:由已知,双曲线的焦点在轴上,且,
又,所以,从而,
所以双曲线的标准方程为
例2已知两地相距800 m,在地听到炮弹爆炸声比在地晚2 s,且声速 为340 m/s,求炮弹爆炸点的轨迹方程.
解:如图3.2-5,建立平面直角坐标系,使两点在轴上,
并且原点与线段的中点重合.
设炮弹爆炸点为,则,
即
又所以, 44 400.
因为,所以点的轨迹是双曲线的右支,因此.
所以,炮弹爆炸点的轨迹方程为
【小组互动】完成课本练习1、2、3、4,同桌交换检查,老师答疑.
【练习答案】
(三)探索与发现、思考与感悟
类型一 双曲线的定义及其应用
1.若双曲线的左、右焦点分别为,点在双曲线上,且则( )
A.11 B.9 C.5 D.3
解:由双曲线的定义,得,即解得 (负值舍去).故选B.
2.设分别是双曲线的左、右焦点,是双曲线上的一点,且,则的面积等于( )
A. B. C.24 D.48
解:由题意得,解得,又,可得为直角三角形,
所以,故选C.
类型二 双曲线标准方程的求法及应用
3. 方程表示双曲线,则的取值范围是( )
A. B. C. D.
解:由双曲线的标准方程,可知
即,故选A.
4. 焦距为,且经过点的双曲线的标准方程为( )
A. B. C. D.
解:因为双曲线经过点,所以为双曲线的一个顶点,故焦点在轴上,且
又,所以双曲线的标准方程为,故选B
5.双曲线上两点的坐标分别为,则此双曲线的标准方程为___________.
解:设双曲线的方程为,则,解得
所以双曲线的标准方程为
答案:
(四)归纳小结,回顾重点
椭圆 双曲线
定 义
标准方程 焦点在轴上, 焦点在轴上, 焦点在轴上, 焦点在轴上,
焦 点 , ,
的关系 ,未必有
(五)作业布置,精炼双基
1.完成课本习题3.2 1、2、5、7、9、10
2.预习3.2.2 双曲线的简单的几何性质
五、教学反思:(课后补充,教学相长)
