第一单元 简易方程(专项卷) 五年级数学下册高频易错题课后强化训练(苏教版含答案)
文档属性
| 名称 | 第一单元 简易方程(专项卷) 五年级数学下册高频易错题课后强化训练(苏教版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 177.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-26 19:31:00 | ||
图片预览



文档简介
第一单元 简易方程(专项卷)
五年级数学下册高频易错题课后强化训练
一、解答题
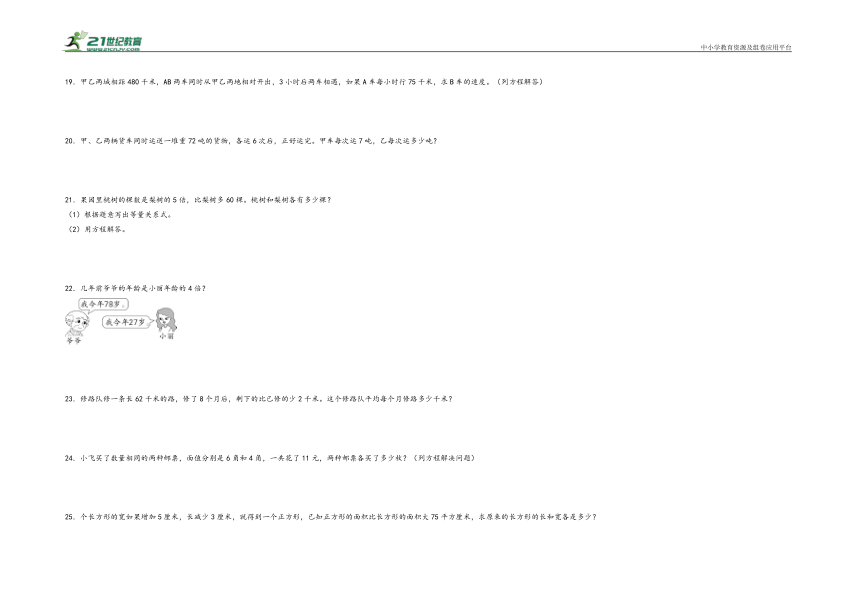
1.高铁时速300千米,比普通列车时速的4倍少20千米。普通列车时速是多少千米?(列方程解答)
2.“南水北调”工程对保护生态资源、促进绿色发展具有重要意义。按照规划,截止到2050年,中线和西线调水总规模为300亿立方米,其中,西线比中线多调水40亿立方米。请问,中线和西线分别调水多少亿立方米?(列方程解决问题)
3.新华小学体育器材室里原来足球的个数是篮球的3倍。体育活动课上,借出了8个足球,现在体育器材室里足球、篮球的数量相同。体育器材室里原有多少个足球?(列方程解答)
4.同学们参观“抗疫英雄事迹展览”,五年级去的人数是四年级的1.6倍,比四年级去的人数多180人。两个年级各去了多少人?(用方程解)
5.2021年6月17日9时22分,我国长征二号F运载火箭搭载神舟十二号载人飞船顺利升空,并取得圆满成功。火箭由四个助推器、芯一级火箭、芯三级火箭、整流罩和逃逸塔组成。火箭高58.34米,是助推器直径的25倍多2.09米,火箭助推器的直径是多少米?(列方程解答)
6.一辆客车和一辆货车同时从连云港车站出发,相背而行。客车的速度是90千米/时,经过2小时,两车相距330千米。求货车的速度。
7.少先队员参加植树活动,六年级植树的棵树是五年级的1.5倍,五年级比六年级少植树72棵。两个年级各植树多少棵?(列方程解答)
8.甲、乙两城相距720千来。两列火车分别从两城同时出发,相向而行,经过3.6小时相遇。从甲城开出的火车平均每小时行驶90千来,从乙城开出的火车每小时行驶多少千米?(列方程解答)
9.南京长江大桥铁路桥长6772米,公路桥长4598米。它的铁路桥比武汉长江铁路桥的5倍多197米。武汉长江大桥铁路桥长多少米?(列方程解题)
10.四、五年级一共有504位同学参加全员核酸检测,五年级的人数是四年级的1.1倍。两个年级各有多少位同学?(列方程解答)
11.动物王国举行运动会。乌龟和兔子赛跑,跑了一段时间,兔子超过了乌龟320米。你能求出兔子跑了多少分钟吗?(列方程解答)
兔子:每分钟跑188米。 乌龟:每分钟跑28米。
12.“书籍是人类进步的阶梯”为了提高孩子们的阅读量,某校六(1)班设置了班级图书角。图书角的人物传记类读物和科普类读物各有多少本?
13.在大同市第四届保护母亲河一一万泉河净水公益活动中,云冈区有0.36万名志愿者参加,比平城区志愿者人数的2倍少0.2万名;云州区比新荣区多0.18万名,云州区的人数是新荣区的1.5倍。
问题一:平城区志愿者有多少万名?
问题二:云州区志愿者有多少万名?
①选问题:我选择的问题是:( )。
②根据所选问题完成下面两个任务。
任务一:根据数量间的相等关系写出等量关系式。
任务二:根据以上数量间的相等关系列方程解决所选问题。
14.看图回答问题。
15.学校买8个篮球和2个足球,一共用了490元,每个篮球45元,每个足球多少元?
16.图书馆买来科技书178本,比故事书的1.8倍少38本,图书馆买来故事书多少本?(用方程解)
17.小丽和笑笑各有一些邮票,已知小丽的邮票数比笑笑的少45枚,笑笑的邮票数量是小丽的2.5倍,她们各有邮票多少枚?(列方程解答)
18.2022年4月16日我国的“神舟”十三号载人飞船顺利返航,结束了183天的太空之旅。在太空时间比“神舟”十二号载人飞船的2倍还多3天。“神舟”十二号载人飞船在太空时间是多少天?
19.甲乙两城相距480千米,AB两车同时从甲乙两地相对开出,3小时后两车相遇,如果A车每小时行75千米,求B车的速度。(列方程解答)
20.甲、乙两辆货车同时运送一堆重72吨的货物,各运6次后,正好运完。甲车每次运7吨,乙每次运多少吨?
21.果园里桃树的棵数是梨树的5倍,比梨树多60棵。桃树和梨树各有多少棵?
(1)根据题意写出等量关系式。
(2)用方程解答。
22.几年前爷爷的年龄是小丽年龄的4倍?
23.修路队修一条长62千米的路,修了8个月后,剩下的比已修的少2千米。这个修路队平均每个月修路多少千米?
24.小飞买了数量相同的两种邮票,面值分别是6角和4角,一共花了11元,两种邮票各买了多少枚?(列方程解决问题)
25.个长方形的宽如果增加5厘米,长减少3厘米,就得到一个正方形,已知正方形的面积比长方形的面积大75平方厘米,求原来的长方形的长和宽各是多少?
参考答案
1.80千米
【分析】设普通列车时速是x千米,根据已知条件“高铁时速300千米,比普通列车时速的4倍少20千米”可知普通列车时速乘4减去20千米就是高铁时速,据此列方程解答即可。
【详解】解:设普通列车时速是x千米。
4x-20=300
4x=320
x=80
答:普通列车时速是80千米。
【点睛】此题主要考查学生根据已知条件找出数量关系式,列方程解决问题的能力。
2.130亿立方米;170亿立方米
【分析】可假设中线调水x亿立方米,那么西线调水则为()亿立方米,再根据等量关系列出方程,解方程即可解答。
【详解】解:设中线调水x亿立方米,则西线调水(x+40)亿立方米
130+40=170(亿立方米)
答:中线调水130亿立方米,西线调水170亿立方米。
【点睛】解答本题的关键是先设定未知数,再根据等量关系列出方程,最后利用等式的性质解方程即可。
3.12个
【分析】根据题意,设体育器材室有篮球x个,足球的个数是篮球的3倍,即足球有3x个;借出了8个足球。体育器材室里足球、篮球的数量相同,足球的个数-3=篮球的个数,列方程:3x-8=x,解方程,即可解答。
【详解】解:设体育器材室里原有x个篮球,则原有3x个足球。
3x-8=x
3x-x=8
2x=8
x=8÷2
x=4
足球有:4×3=12(个)
答:体育器材室里原有12个足球。
【点睛】利用方程的实际应用,根据篮球和足球个数之间的关系,设出未知数,找出相关的量,列方程,解方程。
4.300人;480人
【分析】设四年级去了x人,则五年级去了1.6x人,根据五年级去的人数-四年级去的人数=180,列出方程求出x的值是四年级去的人数,四年级去的人数×1.6=五年级去的人数。
【详解】解:设四年级去了x人。
1.6x-x=180
0.6x÷0.6=180÷0.6
x=300
300×1.6=480(人)
答:四年级去了300人,五年级去了480人。
【点睛】用方程解决问题的关键是找到等量关系。
5.2.25米
【分析】根据“火箭高58.34米,是助推器直径的25倍多2.09米”这一信息,可分析出此题等量关系为:助推器的直径×25+2.09=火箭的高度,设火箭助推器的直径是x米,列出方程并依据等式的性质1和2解答即可。
【详解】解:设火箭助推器的直径是x米。
25x+2.09=58.34
25x+2.09-2.09=58.34-2.09
25x=56.25
25x÷25=56.25÷25
x=2.25
答:火箭助推器的直径是2.25米。
【点睛】此题重点考查列方程解决实际问题的能力,关键是要找准等量关系式。
6.75千米
【分析】设货车的速度是每小时x千米,根据题意可知,两车经过2小时相距330千米,即2小时两车共走了330千米,即90×2+2x=330;据此解答。
【详解】解:设货车的速度是每小时x千米。
90×2+2x=330
180+2x=330
2x=330-180
2x=150
x=75
答:货车的速度是每小时行驶75千米。
【点睛】用方程解答的关键是找准数量关系式。此题中相背而行的路程=客车2小时行驶的路程+货车2小时行驶的路程。
7.144棵;216棵
【分析】设五年级植树x棵,则六年级植树1.5x棵,根据等量关系:六年级植树的棵数-五年级植树的棵数=少植树棵数,列方程解答即可。
【详解】解:设五年级植树x棵,则六年级植树1.5x棵
1.5x-x=72
0.5x=72
x=144
144×1.5=216(棵)
答:五年级植树144棵,六年级植树216棵。
【点睛】本题考查了列方程解应用题,关键是根据等量关系:六年级植树的棵数-五年级植树的棵数=少植树棵数,列方程。
8.110千米
【分析】设从乙城开出的火车每小时行驶x千米,根据题意,(从甲城开出的火车的速度+从乙城开出的火车的速度)×3.6=720列方程解答即可。
【详解】解:设从乙城开出的火车每小时行驶x千米,
(90+x)×3.6=720
90+x=720÷3.6
90+x=200
x=200-90
x=110
答:从乙城开出的火车每小时行驶110千米。
【点睛】此题考查了相遇问题的基本数量关系:速度和×相遇时间=路程。
9.1315米
【分析】根据题意,设武汉长江大桥铁路桥长为x米,武汉长江大桥铁路桥长×5再加上197米,等于南京长江大桥铁路桥长6772米,列方程:5x+197=6772,解方程即可解答。
【详解】解:设武汉长江大桥铁路桥长x米。
5x+197=6772
5x=6772-197
5x=6575
x=6575÷5
x=1315
答:武汉长江大桥铁路桥长1315米。
【点睛】根据方程的实际应用;根据题意,设出未知数,找出相关的量,列出方程,进行解答。
10.四年级有240位同学,五年级有264位同学
【分析】由题意可知,四年级人数×1.1=五年级人数,五年级人数+四年级人数=总人数,据此列出方程,设四年级有x位同学,x+1.1x=504,求解出x的值即可得到四年级的人数,进而求得五年级的人数。
【详解】解:设四年级有x位同学。
x+1.1x=504
2.1x=504
2.1x÷2.1=504÷2.1
x=240
240×1.1=264(位)
答:四年级有240位同学,五年级有264位同学。
【点睛】本题考查了用列方程解决问题。
11.2分钟
【分析】设兔子跑了x分钟,则乌龟也跑了x分钟;兔子每分钟跑188米,x分钟跑了188x米;乌龟每分钟跑28米,x分钟跑了28x米;兔子超过了乌龟320米,即兔子跑的路程减去乌龟跑的路程等于320米,列方程:188x-28x=320,解方程,即可解答。
【详解】解:设兔子跑了x分钟。
188x-28x=320
160x=320
x=320÷160
x=2
答:兔子跑了2分钟。
【点睛】根据方程的实际应用,利用兔子和乌龟跑的路程之间的关系,设出未知数,找出相关的量,列方程,解方程;注意兔子跑的时间与乌龟跑的时间相同。
12.科普类读物有56本,人物传记类读物有84本
【分析】设科普类读物有x本,则人物传记类读物有1.5x本,然后根据等量关系:人物传记类读物的本数+科普类读物的本数=140,据此列方程解答即可。
【详解】解:设科普类读物有x本,则人物传记类读物有1.5x本。
x+1.5x=140
2.5x=140
x=56
56×1.5=84(本)
答:科普类读物有56本,人物传记类读物有84本。
【点睛】本题考查用方程解决实际问题,明确等量关系是解题的关键。
13.我选择的问题是:问题一。平城区志愿者人数×2倍-0.2万=0.36万;0.28万名。
【分析】问题一:根据题意,设平城区志愿者有x万名,云冈区有0.36万名志愿者参加,根据云冈区比比平城区志愿者人数的2倍少0.2万名,即可得到方程(2x-0.2)=0.36,然后解方程,即可得到平城区志愿者有多少万名;
问题二:已知云州区志愿者比新荣区多0.18万名,云州区的人数是新荣区的1.5倍。设新荣区志愿者有y万名,可得出方程:1.5y-y=0.18。
【详解】我选择的问题是:问题一。
平城区志愿者人数×2倍-0.2万=0.36万
解:设平城区志愿者有x万名。
2x-0.2=0.36
2x-0.2+0.2=0.36+0.2
2x÷2=0.56÷2
x=0.28
答:平城区志愿者有0.28万名。
我选择的问题是问题二:云州区志愿者有多少万名?
云州区志愿者人数-新荣区志愿者人数=0.18
解:设新荣区志愿者有y万名。
1.5y-y=0.18
0.5y=0.18
0.5y÷0.5=0.18÷0.5
y=0.36
0.36×1.5=0.54(万名)
答:云州区志愿者有0.54万名。
【点睛】利用方程解决问题的关键是找准题目中的等量关系。
14.11岁
【分析】设小红今年x岁,根据小红年龄×4-2=爸爸年龄,列出方程解答即可。
【详解】解:设小红今年x岁。
4x-2=42
4x-2+2=42+2
4x÷4=44÷4
x=11
答:小红今年11岁。
【点睛】用方程解决问题的关键是找到等量关系。
15.65元
【分析】设每个足球x元,根据单价×数量=总价,分别求出篮球、足球的总价,再根据篮球、足球共用了490元列出方程求解即可。
【详解】解:设每个足球x元。
8×45+2x=490
360+2x=490
360+2x-360=490-360
2x=130
2x÷2=130÷2
x=65
答:每个足球65元。
【点睛】本题主要考查列方程解含有一个未知数的问题。
16.120本
【分析】根据题意,设图书馆买来故事书x本,科技书比故事书的1.8倍少38本,就是故事书×1.8再减去38本等于科技书的本数,列方程:1.8x-38=178,解方程,即可解答。
【详解】解:设图书馆买来故事书x本。
1.8x-38=178
1.8x=178+38
1.8x=216
x=216÷1.8
x=120
答:图书馆买来故事书120本。
【点睛】根据方程的实际应用,利用买来的故事书与科技书之间的关系,设出未知数,列方程,解方程。
17.笑笑:75枚;小丽:30枚
【分析】设小丽的邮票有x枚,笑笑的邮票数量是小丽的2.5倍,则笑笑的邮票有2.5x枚;已知小丽的邮票数比笑笑少45枚,即笑笑邮票的张数-小丽邮票的张数=45枚,列方程:2.5x-x=45,解方程,求出小丽的邮票有多少枚,进而求出笑笑邮票有多少枚,即可解答。
【详解】解:设小丽的邮票有x枚,则笑笑的邮票有2.5x枚。
2.5x-x=45
1.5x=45
x=45÷1.5
x=30
笑笑:30×2.5=75(枚)
答:笑笑的邮票有75枚,小丽的邮票有30枚。
【点睛】本题考查方程的实际应用,利用笑笑和小丽邮票张数的关系,设出未知数,找出相关的量,列方程,解方程。
18.90天
【分析】根据题意,设“神舟”十二号载人飞船在太空时间是x天;“神舟”十三号载人飞船在太空是183天的太空之旅,在太空时间比“神舟”十二号载人飞船的2倍还多3天,即“神舟”十二号载人飞船在太空的天数×2+3=“神舟”十三号载人飞船在太空的183天;列方程:2x+3=183,解方程,即可解答。
【详解】解:设“神舟”十二号载人飞船在太空时间是x天。
2x+3=183
2x=183-3
2x=180
x=180÷2
x=90
答:“神舟”十二号载人飞船在太空时间是90天。
【点睛】根据方程的实际应用,利用“神舟”十三号载人飞船在太空的天数与“神舟”十二号载人飞船在太空的天数之间的关系,设出未知数,找出相关的量,列方程,解方程。
19.85千米/小时
【分析】根据速度和×相遇时间=路程和,可设B车每小时行x千米,据此列出方程:(75+x)×3=480,然后根据等式的性质1和2解出方程即可。
【详解】解:设B车每小时行x千米。
(75+x)×3=480
(75+x)×3÷3=480÷3
75+x=160
75+x-75=160-75
x=85
答:B车每小时行85千米。
【点睛】本题考查了列方程解决问题,找到对应的数量关系式是解题的关键。
20.5吨
【分析】设乙每次运x吨,根据“各运6次后,正好运完”可得等量关系式:(甲每次运的吨数+乙每次运的吨数)×6=72吨,由此列方程求解即可。
【详解】解:设乙每次运x吨
(7+x)×6=72
7+x=12
x=5
答:乙每次运5吨。
【点睛】本题主要考查列方程解含有一个未知数的问题,找出等量关系式是解题的关键。
21.(1)桃树的棵树-梨树的棵树=60
(2)梨树有15棵;桃树有75棵
【分析】根据题意“桃树的棵数是梨树的5倍”设梨树有x棵,则桃树有5x棵,由“桃树的棵数是梨树的5倍,比梨树多60棵”可知:桃树的棵树-梨树的棵树=60,据此列方程解答。
【详解】(1)桃树的棵树-梨树的棵树=60
(2)解:设梨树有x棵,则桃树有5x棵。
5x-x=60
4x=60
x=15
15+60=75(棵)
答:梨树有15棵,桃树有75棵。
【点睛】此题主要考查了列方程解应用题,弄清题意,找出合适的等量关系,进而列出方程是解答此类问题的关键。
22.10年
【分析】设x年前爷爷的年龄是小丽年龄的4倍,用爷爷今年的年龄-x,就是x年前的年龄,用小丽今年的年龄-x,就是小丽x年前的年龄,即爷爷今年的年龄-x=4×(小丽今年的年龄-x),列方程:78-x=4×(27-x),解方程,即可解答。
【详解】解:设x年前爷爷的年龄是小丽年龄的4倍。
78-x=4×(27-x)
78-x=4×27-4x
4x-x=108-78
3x=30
x=30÷3
x=10
答:10年前爷爷的年龄是小丽年龄的4倍。
【点睛】根据方程的实际应用,利用爷爷和小丽年龄之间的关系,设出未知数,找出相关的量,列方程,解方程。
23.4千米
【分析】设修了8个月后,已修的的路程为x千米,则剩下的有x-2千米,根据等量关系:剩下的路程+已修的路程=62,据此列方程求出已修的路程,然后用已修的路程除以修路的时间即可解答。
【详解】解:设修了8个月后,已修的路程为x千米,则剩下的有x-2千米。
x+x-2=62
2x=64
x=32
32÷8=4(千米)
答:这个修路队平均每个月修路4千米。
【点睛】本题考查用方程解决实际问题,求出已修的路程是解题的关键。
24.11枚
【分析】把角换成元,6角=0.6元;4角=0.4元;根据题意,两种邮票数量相同,设邮票的数量各买为x枚,买面值6角邮票需要0.6x元,买面值4角邮票需要0.4x元,一共花了11元,买面值6角的钱数+买面值4角的钱数=11元,列方程:0.6x+0.4x=11,解方程,即可。
【详解】解:设邮票数量各买x枚。
0.6x+0.4x=11
x=11
答:两种邮票各买了11枚。
【点睛】解答本题的关键是明确买的邮票的数量相同,进而设出未知数,列方程,解方程。
25.长:33厘米;宽:25厘米
【分析】由于宽增加5厘米,长减少3厘米就是一个正方形,可以设正方形的边长为x厘米,那么原来长方形的长是:(x+3)厘米,宽是:(x-5)厘米,可以画图来分析,如图所示:正方形的面积比长方形的面积减少了长方形CDFE的面积,增加了长方形AFGH的面积,由于两个面积差是75平方厘米,据此即可列方程,再根据等式的性质解方程即可。
【详解】如下图所示:
解:设正方形的边长为x厘米,那么原来长方形的长是:(x+3)厘米,宽是:(x-5)厘米。
5x-(x-5)×3=75
5x-3x+15=75
2x=75-15
2x=60
x=60÷2
x=30
30+3=33(厘米)
30-5=25(厘米)
答:原来长方形的长是33厘米,宽是25厘米。
中小学教育资源及组卷应用平台
【点睛】本题主要考查组合图形的面积,根据两个长方形的面积的差求出正方形的边长是解答本题的关键。
五年级数学下册高频易错题课后强化训练
一、解答题
1.高铁时速300千米,比普通列车时速的4倍少20千米。普通列车时速是多少千米?(列方程解答)
2.“南水北调”工程对保护生态资源、促进绿色发展具有重要意义。按照规划,截止到2050年,中线和西线调水总规模为300亿立方米,其中,西线比中线多调水40亿立方米。请问,中线和西线分别调水多少亿立方米?(列方程解决问题)
3.新华小学体育器材室里原来足球的个数是篮球的3倍。体育活动课上,借出了8个足球,现在体育器材室里足球、篮球的数量相同。体育器材室里原有多少个足球?(列方程解答)
4.同学们参观“抗疫英雄事迹展览”,五年级去的人数是四年级的1.6倍,比四年级去的人数多180人。两个年级各去了多少人?(用方程解)
5.2021年6月17日9时22分,我国长征二号F运载火箭搭载神舟十二号载人飞船顺利升空,并取得圆满成功。火箭由四个助推器、芯一级火箭、芯三级火箭、整流罩和逃逸塔组成。火箭高58.34米,是助推器直径的25倍多2.09米,火箭助推器的直径是多少米?(列方程解答)
6.一辆客车和一辆货车同时从连云港车站出发,相背而行。客车的速度是90千米/时,经过2小时,两车相距330千米。求货车的速度。
7.少先队员参加植树活动,六年级植树的棵树是五年级的1.5倍,五年级比六年级少植树72棵。两个年级各植树多少棵?(列方程解答)
8.甲、乙两城相距720千来。两列火车分别从两城同时出发,相向而行,经过3.6小时相遇。从甲城开出的火车平均每小时行驶90千来,从乙城开出的火车每小时行驶多少千米?(列方程解答)
9.南京长江大桥铁路桥长6772米,公路桥长4598米。它的铁路桥比武汉长江铁路桥的5倍多197米。武汉长江大桥铁路桥长多少米?(列方程解题)
10.四、五年级一共有504位同学参加全员核酸检测,五年级的人数是四年级的1.1倍。两个年级各有多少位同学?(列方程解答)
11.动物王国举行运动会。乌龟和兔子赛跑,跑了一段时间,兔子超过了乌龟320米。你能求出兔子跑了多少分钟吗?(列方程解答)
兔子:每分钟跑188米。 乌龟:每分钟跑28米。
12.“书籍是人类进步的阶梯”为了提高孩子们的阅读量,某校六(1)班设置了班级图书角。图书角的人物传记类读物和科普类读物各有多少本?
13.在大同市第四届保护母亲河一一万泉河净水公益活动中,云冈区有0.36万名志愿者参加,比平城区志愿者人数的2倍少0.2万名;云州区比新荣区多0.18万名,云州区的人数是新荣区的1.5倍。
问题一:平城区志愿者有多少万名?
问题二:云州区志愿者有多少万名?
①选问题:我选择的问题是:( )。
②根据所选问题完成下面两个任务。
任务一:根据数量间的相等关系写出等量关系式。
任务二:根据以上数量间的相等关系列方程解决所选问题。
14.看图回答问题。
15.学校买8个篮球和2个足球,一共用了490元,每个篮球45元,每个足球多少元?
16.图书馆买来科技书178本,比故事书的1.8倍少38本,图书馆买来故事书多少本?(用方程解)
17.小丽和笑笑各有一些邮票,已知小丽的邮票数比笑笑的少45枚,笑笑的邮票数量是小丽的2.5倍,她们各有邮票多少枚?(列方程解答)
18.2022年4月16日我国的“神舟”十三号载人飞船顺利返航,结束了183天的太空之旅。在太空时间比“神舟”十二号载人飞船的2倍还多3天。“神舟”十二号载人飞船在太空时间是多少天?
19.甲乙两城相距480千米,AB两车同时从甲乙两地相对开出,3小时后两车相遇,如果A车每小时行75千米,求B车的速度。(列方程解答)
20.甲、乙两辆货车同时运送一堆重72吨的货物,各运6次后,正好运完。甲车每次运7吨,乙每次运多少吨?
21.果园里桃树的棵数是梨树的5倍,比梨树多60棵。桃树和梨树各有多少棵?
(1)根据题意写出等量关系式。
(2)用方程解答。
22.几年前爷爷的年龄是小丽年龄的4倍?
23.修路队修一条长62千米的路,修了8个月后,剩下的比已修的少2千米。这个修路队平均每个月修路多少千米?
24.小飞买了数量相同的两种邮票,面值分别是6角和4角,一共花了11元,两种邮票各买了多少枚?(列方程解决问题)
25.个长方形的宽如果增加5厘米,长减少3厘米,就得到一个正方形,已知正方形的面积比长方形的面积大75平方厘米,求原来的长方形的长和宽各是多少?
参考答案
1.80千米
【分析】设普通列车时速是x千米,根据已知条件“高铁时速300千米,比普通列车时速的4倍少20千米”可知普通列车时速乘4减去20千米就是高铁时速,据此列方程解答即可。
【详解】解:设普通列车时速是x千米。
4x-20=300
4x=320
x=80
答:普通列车时速是80千米。
【点睛】此题主要考查学生根据已知条件找出数量关系式,列方程解决问题的能力。
2.130亿立方米;170亿立方米
【分析】可假设中线调水x亿立方米,那么西线调水则为()亿立方米,再根据等量关系列出方程,解方程即可解答。
【详解】解:设中线调水x亿立方米,则西线调水(x+40)亿立方米
130+40=170(亿立方米)
答:中线调水130亿立方米,西线调水170亿立方米。
【点睛】解答本题的关键是先设定未知数,再根据等量关系列出方程,最后利用等式的性质解方程即可。
3.12个
【分析】根据题意,设体育器材室有篮球x个,足球的个数是篮球的3倍,即足球有3x个;借出了8个足球。体育器材室里足球、篮球的数量相同,足球的个数-3=篮球的个数,列方程:3x-8=x,解方程,即可解答。
【详解】解:设体育器材室里原有x个篮球,则原有3x个足球。
3x-8=x
3x-x=8
2x=8
x=8÷2
x=4
足球有:4×3=12(个)
答:体育器材室里原有12个足球。
【点睛】利用方程的实际应用,根据篮球和足球个数之间的关系,设出未知数,找出相关的量,列方程,解方程。
4.300人;480人
【分析】设四年级去了x人,则五年级去了1.6x人,根据五年级去的人数-四年级去的人数=180,列出方程求出x的值是四年级去的人数,四年级去的人数×1.6=五年级去的人数。
【详解】解:设四年级去了x人。
1.6x-x=180
0.6x÷0.6=180÷0.6
x=300
300×1.6=480(人)
答:四年级去了300人,五年级去了480人。
【点睛】用方程解决问题的关键是找到等量关系。
5.2.25米
【分析】根据“火箭高58.34米,是助推器直径的25倍多2.09米”这一信息,可分析出此题等量关系为:助推器的直径×25+2.09=火箭的高度,设火箭助推器的直径是x米,列出方程并依据等式的性质1和2解答即可。
【详解】解:设火箭助推器的直径是x米。
25x+2.09=58.34
25x+2.09-2.09=58.34-2.09
25x=56.25
25x÷25=56.25÷25
x=2.25
答:火箭助推器的直径是2.25米。
【点睛】此题重点考查列方程解决实际问题的能力,关键是要找准等量关系式。
6.75千米
【分析】设货车的速度是每小时x千米,根据题意可知,两车经过2小时相距330千米,即2小时两车共走了330千米,即90×2+2x=330;据此解答。
【详解】解:设货车的速度是每小时x千米。
90×2+2x=330
180+2x=330
2x=330-180
2x=150
x=75
答:货车的速度是每小时行驶75千米。
【点睛】用方程解答的关键是找准数量关系式。此题中相背而行的路程=客车2小时行驶的路程+货车2小时行驶的路程。
7.144棵;216棵
【分析】设五年级植树x棵,则六年级植树1.5x棵,根据等量关系:六年级植树的棵数-五年级植树的棵数=少植树棵数,列方程解答即可。
【详解】解:设五年级植树x棵,则六年级植树1.5x棵
1.5x-x=72
0.5x=72
x=144
144×1.5=216(棵)
答:五年级植树144棵,六年级植树216棵。
【点睛】本题考查了列方程解应用题,关键是根据等量关系:六年级植树的棵数-五年级植树的棵数=少植树棵数,列方程。
8.110千米
【分析】设从乙城开出的火车每小时行驶x千米,根据题意,(从甲城开出的火车的速度+从乙城开出的火车的速度)×3.6=720列方程解答即可。
【详解】解:设从乙城开出的火车每小时行驶x千米,
(90+x)×3.6=720
90+x=720÷3.6
90+x=200
x=200-90
x=110
答:从乙城开出的火车每小时行驶110千米。
【点睛】此题考查了相遇问题的基本数量关系:速度和×相遇时间=路程。
9.1315米
【分析】根据题意,设武汉长江大桥铁路桥长为x米,武汉长江大桥铁路桥长×5再加上197米,等于南京长江大桥铁路桥长6772米,列方程:5x+197=6772,解方程即可解答。
【详解】解:设武汉长江大桥铁路桥长x米。
5x+197=6772
5x=6772-197
5x=6575
x=6575÷5
x=1315
答:武汉长江大桥铁路桥长1315米。
【点睛】根据方程的实际应用;根据题意,设出未知数,找出相关的量,列出方程,进行解答。
10.四年级有240位同学,五年级有264位同学
【分析】由题意可知,四年级人数×1.1=五年级人数,五年级人数+四年级人数=总人数,据此列出方程,设四年级有x位同学,x+1.1x=504,求解出x的值即可得到四年级的人数,进而求得五年级的人数。
【详解】解:设四年级有x位同学。
x+1.1x=504
2.1x=504
2.1x÷2.1=504÷2.1
x=240
240×1.1=264(位)
答:四年级有240位同学,五年级有264位同学。
【点睛】本题考查了用列方程解决问题。
11.2分钟
【分析】设兔子跑了x分钟,则乌龟也跑了x分钟;兔子每分钟跑188米,x分钟跑了188x米;乌龟每分钟跑28米,x分钟跑了28x米;兔子超过了乌龟320米,即兔子跑的路程减去乌龟跑的路程等于320米,列方程:188x-28x=320,解方程,即可解答。
【详解】解:设兔子跑了x分钟。
188x-28x=320
160x=320
x=320÷160
x=2
答:兔子跑了2分钟。
【点睛】根据方程的实际应用,利用兔子和乌龟跑的路程之间的关系,设出未知数,找出相关的量,列方程,解方程;注意兔子跑的时间与乌龟跑的时间相同。
12.科普类读物有56本,人物传记类读物有84本
【分析】设科普类读物有x本,则人物传记类读物有1.5x本,然后根据等量关系:人物传记类读物的本数+科普类读物的本数=140,据此列方程解答即可。
【详解】解:设科普类读物有x本,则人物传记类读物有1.5x本。
x+1.5x=140
2.5x=140
x=56
56×1.5=84(本)
答:科普类读物有56本,人物传记类读物有84本。
【点睛】本题考查用方程解决实际问题,明确等量关系是解题的关键。
13.我选择的问题是:问题一。平城区志愿者人数×2倍-0.2万=0.36万;0.28万名。
【分析】问题一:根据题意,设平城区志愿者有x万名,云冈区有0.36万名志愿者参加,根据云冈区比比平城区志愿者人数的2倍少0.2万名,即可得到方程(2x-0.2)=0.36,然后解方程,即可得到平城区志愿者有多少万名;
问题二:已知云州区志愿者比新荣区多0.18万名,云州区的人数是新荣区的1.5倍。设新荣区志愿者有y万名,可得出方程:1.5y-y=0.18。
【详解】我选择的问题是:问题一。
平城区志愿者人数×2倍-0.2万=0.36万
解:设平城区志愿者有x万名。
2x-0.2=0.36
2x-0.2+0.2=0.36+0.2
2x÷2=0.56÷2
x=0.28
答:平城区志愿者有0.28万名。
我选择的问题是问题二:云州区志愿者有多少万名?
云州区志愿者人数-新荣区志愿者人数=0.18
解:设新荣区志愿者有y万名。
1.5y-y=0.18
0.5y=0.18
0.5y÷0.5=0.18÷0.5
y=0.36
0.36×1.5=0.54(万名)
答:云州区志愿者有0.54万名。
【点睛】利用方程解决问题的关键是找准题目中的等量关系。
14.11岁
【分析】设小红今年x岁,根据小红年龄×4-2=爸爸年龄,列出方程解答即可。
【详解】解:设小红今年x岁。
4x-2=42
4x-2+2=42+2
4x÷4=44÷4
x=11
答:小红今年11岁。
【点睛】用方程解决问题的关键是找到等量关系。
15.65元
【分析】设每个足球x元,根据单价×数量=总价,分别求出篮球、足球的总价,再根据篮球、足球共用了490元列出方程求解即可。
【详解】解:设每个足球x元。
8×45+2x=490
360+2x=490
360+2x-360=490-360
2x=130
2x÷2=130÷2
x=65
答:每个足球65元。
【点睛】本题主要考查列方程解含有一个未知数的问题。
16.120本
【分析】根据题意,设图书馆买来故事书x本,科技书比故事书的1.8倍少38本,就是故事书×1.8再减去38本等于科技书的本数,列方程:1.8x-38=178,解方程,即可解答。
【详解】解:设图书馆买来故事书x本。
1.8x-38=178
1.8x=178+38
1.8x=216
x=216÷1.8
x=120
答:图书馆买来故事书120本。
【点睛】根据方程的实际应用,利用买来的故事书与科技书之间的关系,设出未知数,列方程,解方程。
17.笑笑:75枚;小丽:30枚
【分析】设小丽的邮票有x枚,笑笑的邮票数量是小丽的2.5倍,则笑笑的邮票有2.5x枚;已知小丽的邮票数比笑笑少45枚,即笑笑邮票的张数-小丽邮票的张数=45枚,列方程:2.5x-x=45,解方程,求出小丽的邮票有多少枚,进而求出笑笑邮票有多少枚,即可解答。
【详解】解:设小丽的邮票有x枚,则笑笑的邮票有2.5x枚。
2.5x-x=45
1.5x=45
x=45÷1.5
x=30
笑笑:30×2.5=75(枚)
答:笑笑的邮票有75枚,小丽的邮票有30枚。
【点睛】本题考查方程的实际应用,利用笑笑和小丽邮票张数的关系,设出未知数,找出相关的量,列方程,解方程。
18.90天
【分析】根据题意,设“神舟”十二号载人飞船在太空时间是x天;“神舟”十三号载人飞船在太空是183天的太空之旅,在太空时间比“神舟”十二号载人飞船的2倍还多3天,即“神舟”十二号载人飞船在太空的天数×2+3=“神舟”十三号载人飞船在太空的183天;列方程:2x+3=183,解方程,即可解答。
【详解】解:设“神舟”十二号载人飞船在太空时间是x天。
2x+3=183
2x=183-3
2x=180
x=180÷2
x=90
答:“神舟”十二号载人飞船在太空时间是90天。
【点睛】根据方程的实际应用,利用“神舟”十三号载人飞船在太空的天数与“神舟”十二号载人飞船在太空的天数之间的关系,设出未知数,找出相关的量,列方程,解方程。
19.85千米/小时
【分析】根据速度和×相遇时间=路程和,可设B车每小时行x千米,据此列出方程:(75+x)×3=480,然后根据等式的性质1和2解出方程即可。
【详解】解:设B车每小时行x千米。
(75+x)×3=480
(75+x)×3÷3=480÷3
75+x=160
75+x-75=160-75
x=85
答:B车每小时行85千米。
【点睛】本题考查了列方程解决问题,找到对应的数量关系式是解题的关键。
20.5吨
【分析】设乙每次运x吨,根据“各运6次后,正好运完”可得等量关系式:(甲每次运的吨数+乙每次运的吨数)×6=72吨,由此列方程求解即可。
【详解】解:设乙每次运x吨
(7+x)×6=72
7+x=12
x=5
答:乙每次运5吨。
【点睛】本题主要考查列方程解含有一个未知数的问题,找出等量关系式是解题的关键。
21.(1)桃树的棵树-梨树的棵树=60
(2)梨树有15棵;桃树有75棵
【分析】根据题意“桃树的棵数是梨树的5倍”设梨树有x棵,则桃树有5x棵,由“桃树的棵数是梨树的5倍,比梨树多60棵”可知:桃树的棵树-梨树的棵树=60,据此列方程解答。
【详解】(1)桃树的棵树-梨树的棵树=60
(2)解:设梨树有x棵,则桃树有5x棵。
5x-x=60
4x=60
x=15
15+60=75(棵)
答:梨树有15棵,桃树有75棵。
【点睛】此题主要考查了列方程解应用题,弄清题意,找出合适的等量关系,进而列出方程是解答此类问题的关键。
22.10年
【分析】设x年前爷爷的年龄是小丽年龄的4倍,用爷爷今年的年龄-x,就是x年前的年龄,用小丽今年的年龄-x,就是小丽x年前的年龄,即爷爷今年的年龄-x=4×(小丽今年的年龄-x),列方程:78-x=4×(27-x),解方程,即可解答。
【详解】解:设x年前爷爷的年龄是小丽年龄的4倍。
78-x=4×(27-x)
78-x=4×27-4x
4x-x=108-78
3x=30
x=30÷3
x=10
答:10年前爷爷的年龄是小丽年龄的4倍。
【点睛】根据方程的实际应用,利用爷爷和小丽年龄之间的关系,设出未知数,找出相关的量,列方程,解方程。
23.4千米
【分析】设修了8个月后,已修的的路程为x千米,则剩下的有x-2千米,根据等量关系:剩下的路程+已修的路程=62,据此列方程求出已修的路程,然后用已修的路程除以修路的时间即可解答。
【详解】解:设修了8个月后,已修的路程为x千米,则剩下的有x-2千米。
x+x-2=62
2x=64
x=32
32÷8=4(千米)
答:这个修路队平均每个月修路4千米。
【点睛】本题考查用方程解决实际问题,求出已修的路程是解题的关键。
24.11枚
【分析】把角换成元,6角=0.6元;4角=0.4元;根据题意,两种邮票数量相同,设邮票的数量各买为x枚,买面值6角邮票需要0.6x元,买面值4角邮票需要0.4x元,一共花了11元,买面值6角的钱数+买面值4角的钱数=11元,列方程:0.6x+0.4x=11,解方程,即可。
【详解】解:设邮票数量各买x枚。
0.6x+0.4x=11
x=11
答:两种邮票各买了11枚。
【点睛】解答本题的关键是明确买的邮票的数量相同,进而设出未知数,列方程,解方程。
25.长:33厘米;宽:25厘米
【分析】由于宽增加5厘米,长减少3厘米就是一个正方形,可以设正方形的边长为x厘米,那么原来长方形的长是:(x+3)厘米,宽是:(x-5)厘米,可以画图来分析,如图所示:正方形的面积比长方形的面积减少了长方形CDFE的面积,增加了长方形AFGH的面积,由于两个面积差是75平方厘米,据此即可列方程,再根据等式的性质解方程即可。
【详解】如下图所示:
解:设正方形的边长为x厘米,那么原来长方形的长是:(x+3)厘米,宽是:(x-5)厘米。
5x-(x-5)×3=75
5x-3x+15=75
2x=75-15
2x=60
x=60÷2
x=30
30+3=33(厘米)
30-5=25(厘米)
答:原来长方形的长是33厘米,宽是25厘米。
中小学教育资源及组卷应用平台
【点睛】本题主要考查组合图形的面积,根据两个长方形的面积的差求出正方形的边长是解答本题的关键。
