2022—2023学年人教版数学八年级下册16.3二次根式的加减 课件(共19张PPT)
文档属性
| 名称 | 2022—2023学年人教版数学八年级下册16.3二次根式的加减 课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 510.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-24 00:00:00 | ||
图片预览





文档简介
(共19张PPT)
16.3二次根式的加减法
学习目标
1.熟练进行二次根式的化简
2.会识别同类二次根式并进行合并
3.会利用二次根式的加减法则进行计算
下列根式中,哪些是最简二次根式?
复习回顾
√
×
×
×
×
×
√
√
√
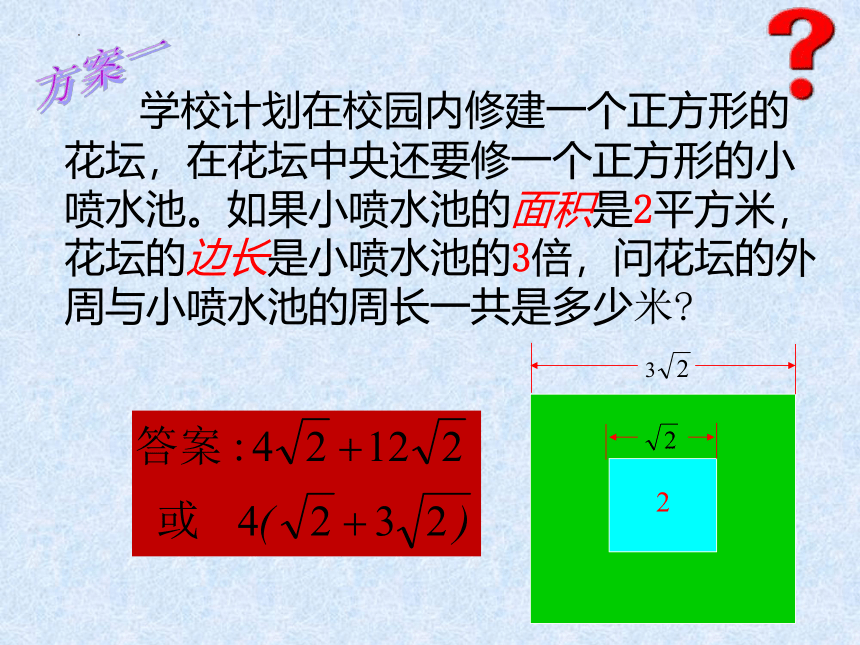
学校计划在校园内修建一个正方形的花坛,在花坛中央还要修一个正方形的小喷水池。如果小喷水池的面积是2平方米,花坛的边长是小喷水池的3倍,问花坛的外周与小喷水池的周长一共是多少米
方案一
2
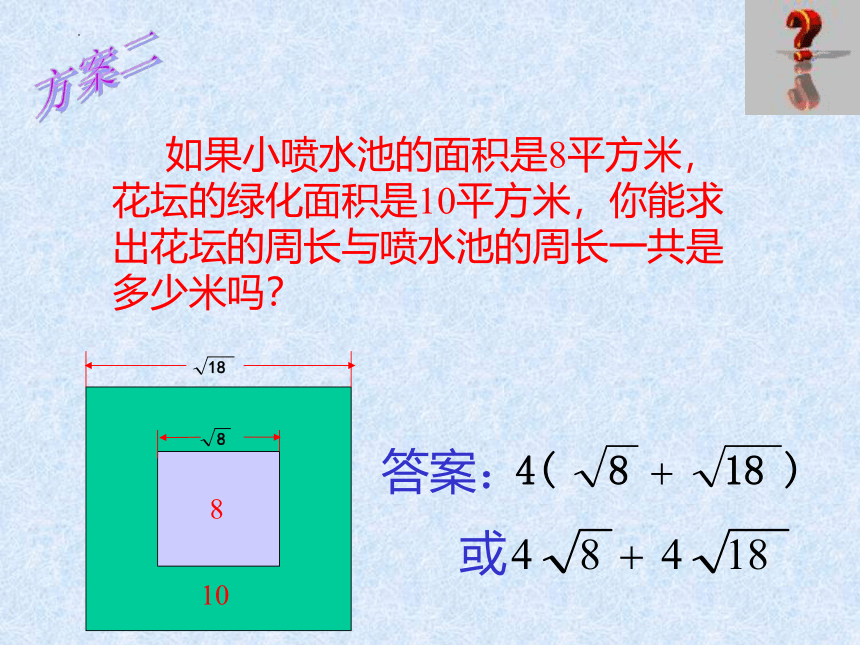
如果小喷水池的面积是8平方米,花坛的绿化面积是10平方米,你能求出花坛的周长与喷水池的周长一共是多少米吗?
方案二
答案:
或
8
10
同类二次根式:
几个二次根式化成___________以后,如果_______相同,这几个二次根式就叫做同类二次根式 。
定义
1.在下列各组根式中,是同类二次根式的是( )
A . B .
D.
3.如果最简二次根式 与 是同类二次根式,求m、n 的值.
125
2. 与 是同类二次根式的是( )
A. B. C. D.
判断几个二次根式是
同类二次根式的方法:
一是化 每个二次根式为最简二次根式;
二是看 化简后的二次根式中被开方数是 否相同。
归纳
(1)两列火车分别运煤2x吨和3x吨,问这两列火车共运多少?_______________
2x +3x=5x吨
(2)两列火车分别运煤2x吨和3y吨,问这两列火车共运多少?_______________
(2x +3y)吨
以下问题你能用同样的方法计算吗?
二次根式加减运算的基本方法
结论1: 如果几个二次根式的被开方数相同, 那么可直接根据分配律进行加减运算。
结论2:如果所给的二次根式不是最简二次根式,应该先化简,再考虑进行加减运算。
概括
…………(分配律)
……………..(化简)
……………..(分配律)
归纳:
(1)把各个二次根式化成最简二次根式
(2)把各个同类二次根式合并.
注意:不是同类二次根式的二次根式
(如 与 )不能合并
判断:下列计算是否正确 为什么
练习
加减法 法则:(1)如果几个二次根式的被开方数相同,那么可以直接根据分配律进行加减运算;
(2)如果所给的二次根式不是最简二次根式,应该先化简,再考虑进行加减运算。
例题讲解
计算:
解:
完成书P13练习1
计算:
加减混合运算,应从左向右依次计算。
探究
解:原式=
别漏了“1”.
化简
如果结果中有分数,必须用假分数表示
解:原式=
课堂小结
1.同类二次根式的定义
2.二次根式加减运算的步骤
3.如何合并同类二次根式
合并同类二次根式与合并同类项类似.
作业
1.课堂作业:13页1,2,3题
2.课外作业:15页1,2,3题
16.3二次根式的加减法
学习目标
1.熟练进行二次根式的化简
2.会识别同类二次根式并进行合并
3.会利用二次根式的加减法则进行计算
下列根式中,哪些是最简二次根式?
复习回顾
√
×
×
×
×
×
√
√
√
学校计划在校园内修建一个正方形的花坛,在花坛中央还要修一个正方形的小喷水池。如果小喷水池的面积是2平方米,花坛的边长是小喷水池的3倍,问花坛的外周与小喷水池的周长一共是多少米
方案一
2
如果小喷水池的面积是8平方米,花坛的绿化面积是10平方米,你能求出花坛的周长与喷水池的周长一共是多少米吗?
方案二
答案:
或
8
10
同类二次根式:
几个二次根式化成___________以后,如果_______相同,这几个二次根式就叫做同类二次根式 。
定义
1.在下列各组根式中,是同类二次根式的是( )
A . B .
D.
3.如果最简二次根式 与 是同类二次根式,求m、n 的值.
125
2. 与 是同类二次根式的是( )
A. B. C. D.
判断几个二次根式是
同类二次根式的方法:
一是化 每个二次根式为最简二次根式;
二是看 化简后的二次根式中被开方数是 否相同。
归纳
(1)两列火车分别运煤2x吨和3x吨,问这两列火车共运多少?_______________
2x +3x=5x吨
(2)两列火车分别运煤2x吨和3y吨,问这两列火车共运多少?_______________
(2x +3y)吨
以下问题你能用同样的方法计算吗?
二次根式加减运算的基本方法
结论1: 如果几个二次根式的被开方数相同, 那么可直接根据分配律进行加减运算。
结论2:如果所给的二次根式不是最简二次根式,应该先化简,再考虑进行加减运算。
概括
…………(分配律)
……………..(化简)
……………..(分配律)
归纳:
(1)把各个二次根式化成最简二次根式
(2)把各个同类二次根式合并.
注意:不是同类二次根式的二次根式
(如 与 )不能合并
判断:下列计算是否正确 为什么
练习
加减法 法则:(1)如果几个二次根式的被开方数相同,那么可以直接根据分配律进行加减运算;
(2)如果所给的二次根式不是最简二次根式,应该先化简,再考虑进行加减运算。
例题讲解
计算:
解:
完成书P13练习1
计算:
加减混合运算,应从左向右依次计算。
探究
解:原式=
别漏了“1”.
化简
如果结果中有分数,必须用假分数表示
解:原式=
课堂小结
1.同类二次根式的定义
2.二次根式加减运算的步骤
3.如何合并同类二次根式
合并同类二次根式与合并同类项类似.
作业
1.课堂作业:13页1,2,3题
2.课外作业:15页1,2,3题
