自5.5.1二倍角公式(共15张PPT)
文档属性
| 名称 | 自5.5.1二倍角公式(共15张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 595.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-24 06:35:49 | ||
图片预览






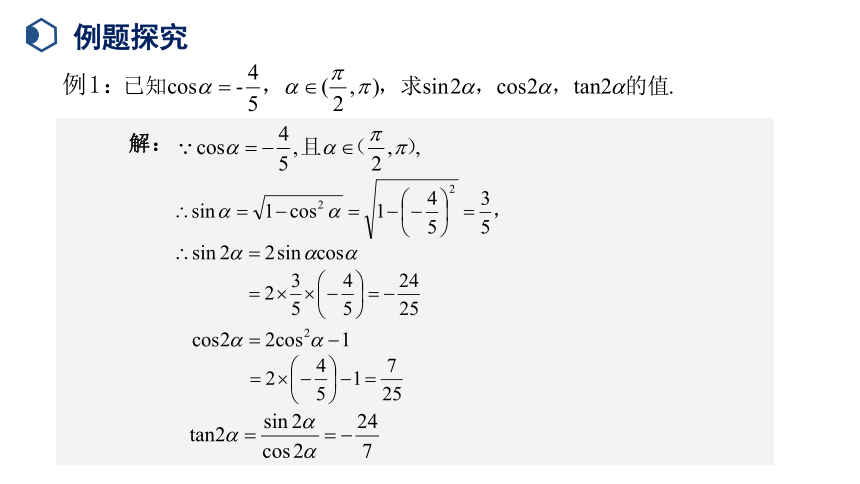
文档简介
(共15张PPT)
5.5.1两角和与差的正弦、余弦和正切公式(3)——二倍角公式
授课老师:某某某
学习目标及重难点
学习目标
1.会推导二倍角的正弦、余弦、正切公式,提升数学抽象、逻辑推理素养;
2.能够灵活运用二倍角公式解决求值和证明等问题,提升数学运算素养.
复习回顾
两角和的正弦、余弦和正切公式
正弦:SCCS
异名积,符号同
余弦:CCSS
同名积,符号反
tan(α-β) =
—————
tanα-tanβ
1+tanαtanβ
tan(α+β) =
—————
tanα+tanβ
1-tanαtanβ
T(α+β)
T(α-β)
先α后β,主角排前
正切:
上和差,下乘积;
符号上同,下反.
sin(α+β) = sinαcosβ+cosαsinβ
sin(α-β) = sinαcosβ-cosαsinβ
S(α+β)
S(α-β)
cos(α+β) = cosαcosβ-sinαsinβ
C(α+β)
C(α-β)
新课引入
探究1:你能利用S(α+β), C(α+β),T(α+β)推导出sin2α,cos2α,tan2α的公式吗?
两角和的正弦公式:
sin(α+β) = sinαcosβ+cosαsinβ
sin2α= sin(α+α)
= sinα cosα + cosα sinα
= 2sinα cosα
二倍角的正弦公式:
sin2α = 2sinα cosα
新课引入
探究2:你能仿照刚刚的推导过程,利用C(α+β),T(α+β)推导出cos2α,tan2α的公式吗?
cos2α= cos(α+α)
= cosα cosα - sinα sinα
= cos2α - sin2α
tan2α= tan(α+α)
2tanα
1 - tan2α
tanα + tanα
1 - tanα tanα
= ——————
= ————
追问:如果要求二倍角的余弦公式C(2α)中仅含α的正弦(余弦),那么C(2α)还有其他的表示吗?
由 cos2α = cos2α - sin2α ,
cos2α + sin2α =1
得 cos2α = 2cos2α - 1 ,
或 cos2α = 1-2sin2α.
二倍角公式
S(2α)
sin2α = 2sinα cosα
C(2α)
cos2α = cos2α - sin2α
= 2cos2α - 1
= 1-2sin2α
tan2α = ————
2tanα
1 - tan2α
T(2α)
思考:观察二倍角公式,有何结构特征?
①从左向右:升幂缩角;
从右向左:降幂扩角.
②正弦是单项式,余弦是
多项式,正切是分式.
以上这些公式都叫做倍角公式.
注:这里的“倍角”专指“二倍角”,遇到“三倍角”等名词时,“三”字等不能省略.
例题探究
例1:
解:
例题探究
例2:
(1) sin4α = 2sin( )cos( );
(2) sinα = 2sin( )cos( );
(3) cos6α = ( ) - ( )
= 2( ) - 1
=1 - ( )
(4) = tan( );
“倍”是描述两个数量之间关系的, 是 的二倍, 是 的二倍, 是 二倍,这里蕴含着换元思想.
例题探究
例3:
已知sin2α=,求sin4α,cos4α,tan4α的值.
例题探究
例4:
已知cos2α=,求cosα的值.
解:
追问:已知cos2α时,能否求出sinα的值呢?
由 cos2α = 1-2sin2α,
由 cos2α = 2cos2α - 1 ,
公式变形
公式特点:降幂升角
cos2α =
sin2α =
例题探究
例5:
解法1:
例题探究
例5:
解法2:
练习巩固
解:
(5)
(5)
课堂小结
两角差的余弦公式
02变形
01倍角公式
S(2α)
sin2α = 2sinα cosα
C(2α)
cos2α = cos2α - sin2α
tan2α = ————
2tanα
1 - tan2α
T(2α)
cos2α =
sin2α =
5.5.1两角和与差的正弦、余弦和正切公式(3)——二倍角公式
授课老师:某某某
学习目标及重难点
学习目标
1.会推导二倍角的正弦、余弦、正切公式,提升数学抽象、逻辑推理素养;
2.能够灵活运用二倍角公式解决求值和证明等问题,提升数学运算素养.
复习回顾
两角和的正弦、余弦和正切公式
正弦:SCCS
异名积,符号同
余弦:CCSS
同名积,符号反
tan(α-β) =
—————
tanα-tanβ
1+tanαtanβ
tan(α+β) =
—————
tanα+tanβ
1-tanαtanβ
T(α+β)
T(α-β)
先α后β,主角排前
正切:
上和差,下乘积;
符号上同,下反.
sin(α+β) = sinαcosβ+cosαsinβ
sin(α-β) = sinαcosβ-cosαsinβ
S(α+β)
S(α-β)
cos(α+β) = cosαcosβ-sinαsinβ
C(α+β)
C(α-β)
新课引入
探究1:你能利用S(α+β), C(α+β),T(α+β)推导出sin2α,cos2α,tan2α的公式吗?
两角和的正弦公式:
sin(α+β) = sinαcosβ+cosαsinβ
sin2α= sin(α+α)
= sinα cosα + cosα sinα
= 2sinα cosα
二倍角的正弦公式:
sin2α = 2sinα cosα
新课引入
探究2:你能仿照刚刚的推导过程,利用C(α+β),T(α+β)推导出cos2α,tan2α的公式吗?
cos2α= cos(α+α)
= cosα cosα - sinα sinα
= cos2α - sin2α
tan2α= tan(α+α)
2tanα
1 - tan2α
tanα + tanα
1 - tanα tanα
= ——————
= ————
追问:如果要求二倍角的余弦公式C(2α)中仅含α的正弦(余弦),那么C(2α)还有其他的表示吗?
由 cos2α = cos2α - sin2α ,
cos2α + sin2α =1
得 cos2α = 2cos2α - 1 ,
或 cos2α = 1-2sin2α.
二倍角公式
S(2α)
sin2α = 2sinα cosα
C(2α)
cos2α = cos2α - sin2α
= 2cos2α - 1
= 1-2sin2α
tan2α = ————
2tanα
1 - tan2α
T(2α)
思考:观察二倍角公式,有何结构特征?
①从左向右:升幂缩角;
从右向左:降幂扩角.
②正弦是单项式,余弦是
多项式,正切是分式.
以上这些公式都叫做倍角公式.
注:这里的“倍角”专指“二倍角”,遇到“三倍角”等名词时,“三”字等不能省略.
例题探究
例1:
解:
例题探究
例2:
(1) sin4α = 2sin( )cos( );
(2) sinα = 2sin( )cos( );
(3) cos6α = ( ) - ( )
= 2( ) - 1
=1 - ( )
(4) = tan( );
“倍”是描述两个数量之间关系的, 是 的二倍, 是 的二倍, 是 二倍,这里蕴含着换元思想.
例题探究
例3:
已知sin2α=,求sin4α,cos4α,tan4α的值.
例题探究
例4:
已知cos2α=,求cosα的值.
解:
追问:已知cos2α时,能否求出sinα的值呢?
由 cos2α = 1-2sin2α,
由 cos2α = 2cos2α - 1 ,
公式变形
公式特点:降幂升角
cos2α =
sin2α =
例题探究
例5:
解法1:
例题探究
例5:
解法2:
练习巩固
解:
(5)
(5)
课堂小结
两角差的余弦公式
02变形
01倍角公式
S(2α)
sin2α = 2sinα cosα
C(2α)
cos2α = cos2α - sin2α
tan2α = ————
2tanα
1 - tan2α
T(2α)
cos2α =
sin2α =
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
