高二数学人教A版(2019)选择性必修第一册 2.3.1 两条直线的交点坐标 2.3.2 两点间的距离公式 课件(共30张PPT)
文档属性
| 名称 | 高二数学人教A版(2019)选择性必修第一册 2.3.1 两条直线的交点坐标 2.3.2 两点间的距离公式 课件(共30张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 11.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-24 13:06:11 | ||
图片预览


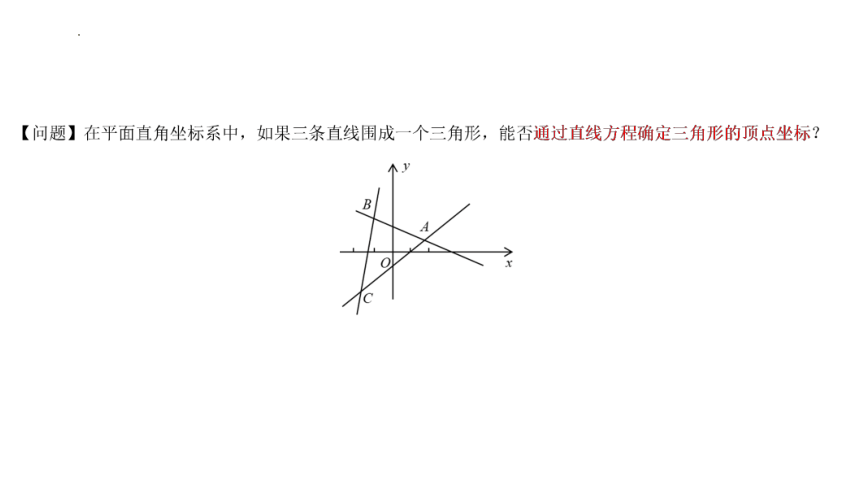




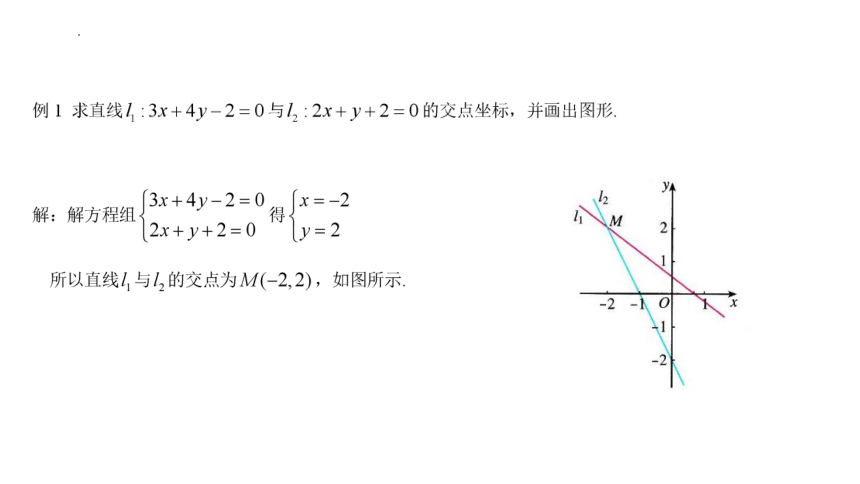




文档简介
(共30张PPT)
第二章
2.3.1 两条直线的交点坐标
2.3.2 两点间的距离公式
直线和圆的方程
(一)
创设情景
揭示课题
(二)
阅读精要
研讨新知
例题研讨
学习例题的正规表达
学习例题的常规方法
从例题中学会思考
如何看例题
小组互动
例题研讨
学习例题的正规表达
学习例题的常规方法
从例题中学会思考
如何看例题
小组互动
(三)
探索与发现
思考与感悟
(四)
归纳小结
回顾重点
(五)
作业布置
精炼双基
千里之行始于足下
2022
昵图网nipic.com/风之雨
昵图网山uw.nipic.comY:sdoublEye
N0:201205070854322631B1
练习(第72页)
1.(①)(,),
图略;(2)(2,3),图略.
2.(1)直线11与l2相交,交点坐标为
侣》:
(2)直线l1与12是同一条直线,即它们重合;
(3)11∥2
4
3.y
-34.
练习(第74页)
1.(1)|AB|=8,(2)CD=3;(3)|PQ|=2√10;(4)|MN=√13.
2.a=士8.
3.如图,在Rt△ABC中,点M是斜边AB的中点.以直角顶点C
为原点,两条直角边AC,BC所在直线为x轴、y轴,建立坐标系.在
B
M
R△ABC中,有C(0,0,设A(a,0),B(0,b),则有M(g,名):
oc)
MC=√(8)+(合)-2Va+B,AB1=Va+6,所以MA=
(第3题)
MB=)√a2+b.所以,直角三角形斜边的中点到三个顶点的距离相等.
三
l山
S
第二章
2.3.1 两条直线的交点坐标
2.3.2 两点间的距离公式
直线和圆的方程
(一)
创设情景
揭示课题
(二)
阅读精要
研讨新知
例题研讨
学习例题的正规表达
学习例题的常规方法
从例题中学会思考
如何看例题
小组互动
例题研讨
学习例题的正规表达
学习例题的常规方法
从例题中学会思考
如何看例题
小组互动
(三)
探索与发现
思考与感悟
(四)
归纳小结
回顾重点
(五)
作业布置
精炼双基
千里之行始于足下
2022
昵图网nipic.com/风之雨
昵图网山uw.nipic.comY:sdoublEye
N0:201205070854322631B1
练习(第72页)
1.(①)(,),
图略;(2)(2,3),图略.
2.(1)直线11与l2相交,交点坐标为
侣》:
(2)直线l1与12是同一条直线,即它们重合;
(3)11∥2
4
3.y
-34.
练习(第74页)
1.(1)|AB|=8,(2)CD=3;(3)|PQ|=2√10;(4)|MN=√13.
2.a=士8.
3.如图,在Rt△ABC中,点M是斜边AB的中点.以直角顶点C
为原点,两条直角边AC,BC所在直线为x轴、y轴,建立坐标系.在
B
M
R△ABC中,有C(0,0,设A(a,0),B(0,b),则有M(g,名):
oc)
MC=√(8)+(合)-2Va+B,AB1=Va+6,所以MA=
(第3题)
MB=)√a2+b.所以,直角三角形斜边的中点到三个顶点的距离相等.
三
l山
S
