2022-2023学年(人教版)初中数学九年级下册26.1.2 反比例函数的图象和性质第2课时 课件(共36张PPT)
文档属性
| 名称 | 2022-2023学年(人教版)初中数学九年级下册26.1.2 反比例函数的图象和性质第2课时 课件(共36张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-24 00:00:00 | ||
图片预览










文档简介
(共36张PPT)
第2课时 反比例函数的图象和性质(2)
——反比例函数的图象和性质的运用
R·九年级下册
问题1 反比例函数 ① ;② ;
③ ;④ 的图象:
(1)位于第一、三象限的是 ;
(2)位于第二、四象限的是 .
② ④
① ③
复习导入
问题2 在反比例函数① ;② ;③
; ④ 的图象中,(x1,y1)
(x2,y2)是它们的图象上的两个点,并且在同一象限内:
(1)若 x1<x2 ,则 y1<y2 的函数是 ;
(2)若 x1<x2 ,则 y1>y2 的函数是 .
② ④
① ③
反比例函数的图象和性质的运用
知识点
例3 已知反比例函数的图象经过点 A(2,6).
(1)这个函数的图象位于哪些象限?y 随 x 的增大如何变化?
(2)点 B(3,4),C( , ),D(2,5)是否在这个函数的图象上?
推进新课
解:(1)因为点 A(2,6)在第一象限 ,所以这个函数的图象位于第一、三象限,在每一个象限内,y 随 x 的增大而减小.
(2)设这个反比例函数的解析式为 ,因为点 A(2,6)在其图象上,所以点 A 的坐标满足 ,即
解得 k = 12.
待定系数法
若点(a,b)在 的图象上,则ab = ___.
k
所以,这个反比例函数的解析式为 .
因为点 B,C 的坐标都满足 ,点 D 的坐标不满足 ,
所以点 B,C 在函数 的图象上,点 D 不在这个函数的图象上.
1.已知一个反比例函数的图象经过点 A(3, – 4).
(1)这个函数的图象位于哪些象限?在图象的每一支上,y 随 x 的增大如何变化?
(2)点 B( – 3,4),C( – 2,6),D(3,4)是否在这个函数的图象上?为什么?
第二、第四象限
增大
点 B、C 在这个函数图象上,点 D 不在这个函数的图象上.
练习
(2)若点(a,b)满足解析式 (即ab = k),则点(a,b)在此函数的图象上.
(1)反比例函数的图象上一点的坐标
判断其图象所在的象限.
根据图象说性质.
归纳
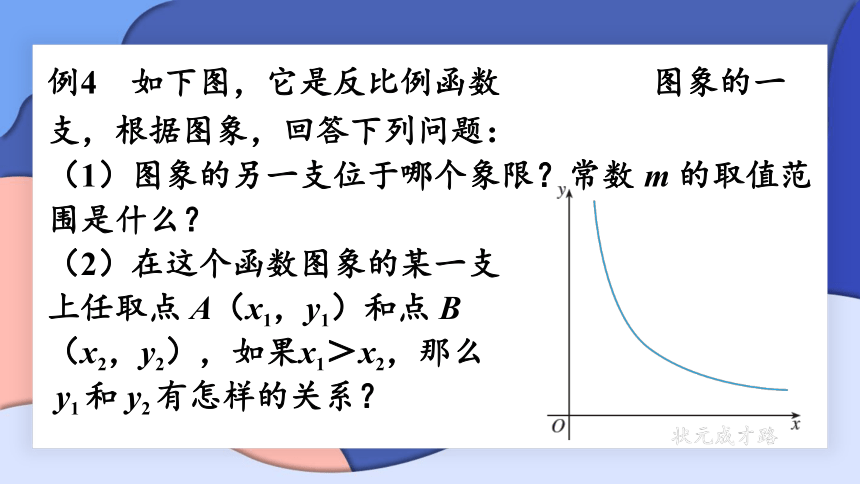
例4 如下图,它是反比例函数 图象的一支,根据图象,回答下列问题:
(1)图象的另一支位于哪个象限?常数 m 的取值范围是什么?
(2)在这个函数图象的某一支
上任取点 A(x1,y1)和点 B
(x2,y2),如果x1>x2,那么
y1 和 y2 有怎样的关系?
解:(1)反比例函数的图象只有两种可能:位于第一、第三象限,或者位于第二、第四象限.因为这个函数的图象的一支位于第一象限,所以另一支必位于第三象限.
因为这个函数的图象位于第一、第三象限,所以
m – 5 >0
解得 m>5.
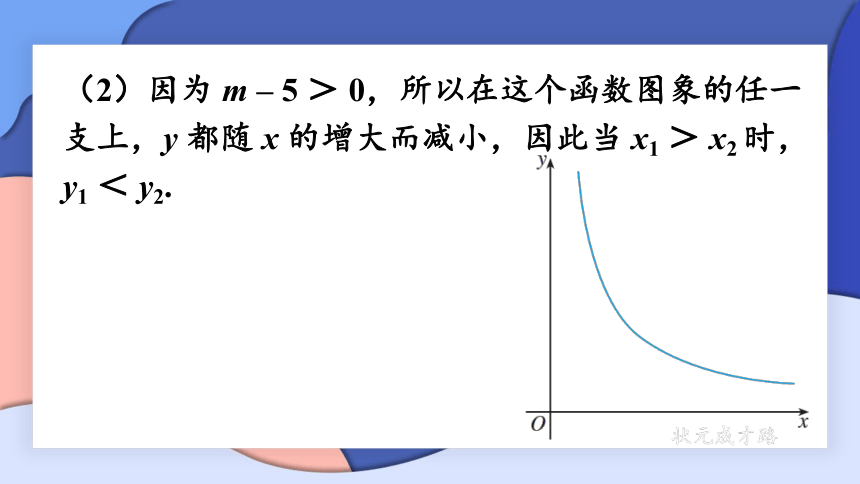
(2)因为 m – 5 > 0,所以在这个函数图象的任一支上,y 都随 x 的增大而减小,因此当 x1 > x2 时,y1 < y2.
1.反比例函数 的图象既是________对称图形,其对称中心是________,又是_____对称图形,其对称轴是直线________________ .
中心
原点
轴
y = x和y = – x
试一试
2.如图是反比例函数 的图象的一支,根据图象回答问题:
(1)图象的另一支位于哪个象限,常数 n 的取值范围是什么?
(2)在这个函数图象的某一支上任取点 A(a,b),B(a',b'),如果 a<a',那么 b 与 b'的大小关系如何?为什么?
解:(1)图象的另一支位于第四象限,n < – 7.
(2) ∵k = n + 7<0,∴在这个函数图象的任一支上,y 都随 x 的增大而增大,
∴a<a' 时,b<b'.
2.已知点A(x1,y1),B(x2,y2)在反比例函数 的图象上.如果 x1<x2,而且 x1,x2 同号,那么 y1,y2 有怎样的大小关系?为什么?
解:y1>y2.
因为函数 的图象位于第一、第三象限,所以在每个象限内,y 随 x 的增大而减小.因为 x1<x2,所以 y1>y2.
练习
1.如果点(3, – 4)在反比例函数 的图象上,那么下列各点中,在此图象上的是( )
A.( 3,4) B.(– 2, – 6)
C.(– 2,6) D.(– 3, – 4)
C
基础巩固
随堂演练
2.(多选)函数 y = kx 和 (k ≠ 0)的图象在同一平面直角坐标系中大致是( )
BD
3.正比例函数 y = x 的图象与反比例函数
的图象有一个交点的纵坐标是 2,求:
(1)当 x = – 3 时,反比例函数 的值;
(2)当 – 3<x< – 1 时,反比例函数 的取值范围.
综合应用
解:(1)由题意知:正比例函数与反比例函数图象的一个交点是(2,2),则 k = 2×2 = 4,即反比例函数的解析式为 .当 x = – 3 时,
(2)当 – 3<x< – 1 时,反比例函数的图象在第三象限,y 随 x 的增大而减小,又∵当 x = – 1 时,y = – 4,
1. 已知反比例函数图象及图象上两点横坐标的大小,如何比较纵坐标的大小?反之呢?
课堂小结
解:k >0时,如果 x1<x2<0或0<x1<x2 ,那么 y1 > y2;如果 x1<0<x2 ,那么 y1 <0< y2;
k < 0时,如果 x1<x2<0或0<x1<x2 ,那么 y1 < y2;如果 x1<0<x2 ,那么 y1 > 0 > y2.
2. 在反比例函数图象及性质的应用中体现了数形结合思想,能否谈谈你的体会?
已知点 A(x1,y1)、B(x2,y2)是反比例函数 (k>0)图象上的两点,若 x1<0<x2,则有( )
A.y1<0<y2 B.y2<0<y1
C.y1<y2<0 D.y2<y1<0
拓展延伸
A
1.写出函数解析式表示下列关系,并指出它们各是什么函数:
(1)体积是常数 V 时,圆柱的底面积 S 与高 h 的关系;
(2)柳树乡共有耕地 S hm2,该乡人均耕地面积 y (hm2/人)与全乡总人口 x 的关系.
复习巩固
它们都是反比例函数.
习题26.1
2.下列函数中是反比例函数的是( ).
(A) (B)
(C)y = x2 (D)
B
3.填空:
(1)反比例函数 的图象如图(1)所示,则 k ____ 0,在图象的每一支上,y 随 x 的增大而________ ;
(2)反比例函数 的图象如图(2)所示,则 k ____ 0,在图象的每一支上,y 随 x 的增大而________ ;
>
减小
<
增大
3.填空:
(3)若点(1,3)在反比例函数 的图象上,则 k = ____ ,在图象的每一支上,y 随 x 的增大而________.
3
减小
4.如果 y 是 x 的反比例函数,那么 x 也是 y 的反比例函数吗?
解:如果 y 是 x 的反比例函数,那么
(k ≠ 0),可化为 (k ≠ 0),所以 x 也是 y 的反比例函数.
5.正比例函数 y = x 的图象与反比例函数
的图象有一个交点的纵坐标是 2.
(1)当 x = – 3 时,求反比例函数 的值;
(2)当 – 3<x< – 1时,求反比例函数 的取值范围.
综合运用
解:(1)由题意知:正比例函数与反比例函数图象的一个交点是(2,2),则 k = 2×2 = 4,即反比例函数的解析式为 .当 x = – 3 时,
(2)当 – 3<x< – 1时,反比例函数的图象在第三象限,y 随 x 的增大而减小,又∵当 x = – 1 时,y = – 4,
6.如果 y 是 z 的反比例函数,z 是 x 的反比例函数,那么 y 与 x 具有怎样的函数关系?
解:根据题意,不妨设 (k1≠ 0),
(k2 ≠ 0),则
即 y 是 x 的正比例函数.
7.如果 y 是 z 的反比例函数,z 是 x的正比例函数,且 x ≠ 0,那么 y 与 x 具有怎样的函数关系?
解:根据题意,不妨设 (k1≠ 0),
z = k2x(k2 ≠ 0),则
即 y 是 x 的反比例函数.
8.在同一直角坐标系中,函数 y = kx 和 (k ≠ 0)的图象大致是( )
(A)(1)(2) (B)(1)(3)
(C)(2)(4) (D)(3)(4)
C
拓广探索
9.已知反比例函数 的图象的一支位于第一象限.
(1)图象的另一支位于哪个象限?常数ω的取值范围是什么?
(2)在这个函数图象上任取点 A(x1,y1)和 B(x2,y2).如果 y1> y2,那么 x1 与 x2 有怎样的大小关系?
解:(1)反比例函数的图象分布只有两种可能,分布在第一、三象限,或者分布在第二、四象限,因为函数 的图象的一支在第一象限,则图象的另一支一定在第三象限.
解: (2)
∴ ①在这个函数图象的任一支上,y 随 x 的增大而减小.如果 y1>y2,那么 x1<x2.
②在这个函数图象的不同支上,如果 y1>y2,那么 x1 > x2.
第2课时 反比例函数的图象和性质(2)
——反比例函数的图象和性质的运用
R·九年级下册
问题1 反比例函数 ① ;② ;
③ ;④ 的图象:
(1)位于第一、三象限的是 ;
(2)位于第二、四象限的是 .
② ④
① ③
复习导入
问题2 在反比例函数① ;② ;③
; ④ 的图象中,(x1,y1)
(x2,y2)是它们的图象上的两个点,并且在同一象限内:
(1)若 x1<x2 ,则 y1<y2 的函数是 ;
(2)若 x1<x2 ,则 y1>y2 的函数是 .
② ④
① ③
反比例函数的图象和性质的运用
知识点
例3 已知反比例函数的图象经过点 A(2,6).
(1)这个函数的图象位于哪些象限?y 随 x 的增大如何变化?
(2)点 B(3,4),C( , ),D(2,5)是否在这个函数的图象上?
推进新课
解:(1)因为点 A(2,6)在第一象限 ,所以这个函数的图象位于第一、三象限,在每一个象限内,y 随 x 的增大而减小.
(2)设这个反比例函数的解析式为 ,因为点 A(2,6)在其图象上,所以点 A 的坐标满足 ,即
解得 k = 12.
待定系数法
若点(a,b)在 的图象上,则ab = ___.
k
所以,这个反比例函数的解析式为 .
因为点 B,C 的坐标都满足 ,点 D 的坐标不满足 ,
所以点 B,C 在函数 的图象上,点 D 不在这个函数的图象上.
1.已知一个反比例函数的图象经过点 A(3, – 4).
(1)这个函数的图象位于哪些象限?在图象的每一支上,y 随 x 的增大如何变化?
(2)点 B( – 3,4),C( – 2,6),D(3,4)是否在这个函数的图象上?为什么?
第二、第四象限
增大
点 B、C 在这个函数图象上,点 D 不在这个函数的图象上.
练习
(2)若点(a,b)满足解析式 (即ab = k),则点(a,b)在此函数的图象上.
(1)反比例函数的图象上一点的坐标
判断其图象所在的象限.
根据图象说性质.
归纳
例4 如下图,它是反比例函数 图象的一支,根据图象,回答下列问题:
(1)图象的另一支位于哪个象限?常数 m 的取值范围是什么?
(2)在这个函数图象的某一支
上任取点 A(x1,y1)和点 B
(x2,y2),如果x1>x2,那么
y1 和 y2 有怎样的关系?
解:(1)反比例函数的图象只有两种可能:位于第一、第三象限,或者位于第二、第四象限.因为这个函数的图象的一支位于第一象限,所以另一支必位于第三象限.
因为这个函数的图象位于第一、第三象限,所以
m – 5 >0
解得 m>5.
(2)因为 m – 5 > 0,所以在这个函数图象的任一支上,y 都随 x 的增大而减小,因此当 x1 > x2 时,y1 < y2.
1.反比例函数 的图象既是________对称图形,其对称中心是________,又是_____对称图形,其对称轴是直线________________ .
中心
原点
轴
y = x和y = – x
试一试
2.如图是反比例函数 的图象的一支,根据图象回答问题:
(1)图象的另一支位于哪个象限,常数 n 的取值范围是什么?
(2)在这个函数图象的某一支上任取点 A(a,b),B(a',b'),如果 a<a',那么 b 与 b'的大小关系如何?为什么?
解:(1)图象的另一支位于第四象限,n < – 7.
(2) ∵k = n + 7<0,∴在这个函数图象的任一支上,y 都随 x 的增大而增大,
∴a<a' 时,b<b'.
2.已知点A(x1,y1),B(x2,y2)在反比例函数 的图象上.如果 x1<x2,而且 x1,x2 同号,那么 y1,y2 有怎样的大小关系?为什么?
解:y1>y2.
因为函数 的图象位于第一、第三象限,所以在每个象限内,y 随 x 的增大而减小.因为 x1<x2,所以 y1>y2.
练习
1.如果点(3, – 4)在反比例函数 的图象上,那么下列各点中,在此图象上的是( )
A.( 3,4) B.(– 2, – 6)
C.(– 2,6) D.(– 3, – 4)
C
基础巩固
随堂演练
2.(多选)函数 y = kx 和 (k ≠ 0)的图象在同一平面直角坐标系中大致是( )
BD
3.正比例函数 y = x 的图象与反比例函数
的图象有一个交点的纵坐标是 2,求:
(1)当 x = – 3 时,反比例函数 的值;
(2)当 – 3<x< – 1 时,反比例函数 的取值范围.
综合应用
解:(1)由题意知:正比例函数与反比例函数图象的一个交点是(2,2),则 k = 2×2 = 4,即反比例函数的解析式为 .当 x = – 3 时,
(2)当 – 3<x< – 1 时,反比例函数的图象在第三象限,y 随 x 的增大而减小,又∵当 x = – 1 时,y = – 4,
1. 已知反比例函数图象及图象上两点横坐标的大小,如何比较纵坐标的大小?反之呢?
课堂小结
解:k >0时,如果 x1<x2<0或0<x1<x2 ,那么 y1 > y2;如果 x1<0<x2 ,那么 y1 <0< y2;
k < 0时,如果 x1<x2<0或0<x1<x2 ,那么 y1 < y2;如果 x1<0<x2 ,那么 y1 > 0 > y2.
2. 在反比例函数图象及性质的应用中体现了数形结合思想,能否谈谈你的体会?
已知点 A(x1,y1)、B(x2,y2)是反比例函数 (k>0)图象上的两点,若 x1<0<x2,则有( )
A.y1<0<y2 B.y2<0<y1
C.y1<y2<0 D.y2<y1<0
拓展延伸
A
1.写出函数解析式表示下列关系,并指出它们各是什么函数:
(1)体积是常数 V 时,圆柱的底面积 S 与高 h 的关系;
(2)柳树乡共有耕地 S hm2,该乡人均耕地面积 y (hm2/人)与全乡总人口 x 的关系.
复习巩固
它们都是反比例函数.
习题26.1
2.下列函数中是反比例函数的是( ).
(A) (B)
(C)y = x2 (D)
B
3.填空:
(1)反比例函数 的图象如图(1)所示,则 k ____ 0,在图象的每一支上,y 随 x 的增大而________ ;
(2)反比例函数 的图象如图(2)所示,则 k ____ 0,在图象的每一支上,y 随 x 的增大而________ ;
>
减小
<
增大
3.填空:
(3)若点(1,3)在反比例函数 的图象上,则 k = ____ ,在图象的每一支上,y 随 x 的增大而________.
3
减小
4.如果 y 是 x 的反比例函数,那么 x 也是 y 的反比例函数吗?
解:如果 y 是 x 的反比例函数,那么
(k ≠ 0),可化为 (k ≠ 0),所以 x 也是 y 的反比例函数.
5.正比例函数 y = x 的图象与反比例函数
的图象有一个交点的纵坐标是 2.
(1)当 x = – 3 时,求反比例函数 的值;
(2)当 – 3<x< – 1时,求反比例函数 的取值范围.
综合运用
解:(1)由题意知:正比例函数与反比例函数图象的一个交点是(2,2),则 k = 2×2 = 4,即反比例函数的解析式为 .当 x = – 3 时,
(2)当 – 3<x< – 1时,反比例函数的图象在第三象限,y 随 x 的增大而减小,又∵当 x = – 1 时,y = – 4,
6.如果 y 是 z 的反比例函数,z 是 x 的反比例函数,那么 y 与 x 具有怎样的函数关系?
解:根据题意,不妨设 (k1≠ 0),
(k2 ≠ 0),则
即 y 是 x 的正比例函数.
7.如果 y 是 z 的反比例函数,z 是 x的正比例函数,且 x ≠ 0,那么 y 与 x 具有怎样的函数关系?
解:根据题意,不妨设 (k1≠ 0),
z = k2x(k2 ≠ 0),则
即 y 是 x 的反比例函数.
8.在同一直角坐标系中,函数 y = kx 和 (k ≠ 0)的图象大致是( )
(A)(1)(2) (B)(1)(3)
(C)(2)(4) (D)(3)(4)
C
拓广探索
9.已知反比例函数 的图象的一支位于第一象限.
(1)图象的另一支位于哪个象限?常数ω的取值范围是什么?
(2)在这个函数图象上任取点 A(x1,y1)和 B(x2,y2).如果 y1> y2,那么 x1 与 x2 有怎样的大小关系?
解:(1)反比例函数的图象分布只有两种可能,分布在第一、三象限,或者分布在第二、四象限,因为函数 的图象的一支在第一象限,则图象的另一支一定在第三象限.
解: (2)
∴ ①在这个函数图象的任一支上,y 随 x 的增大而减小.如果 y1>y2,那么 x1<x2.
②在这个函数图象的不同支上,如果 y1>y2,那么 x1 > x2.
