探索三角形全等的条件１[下学期]

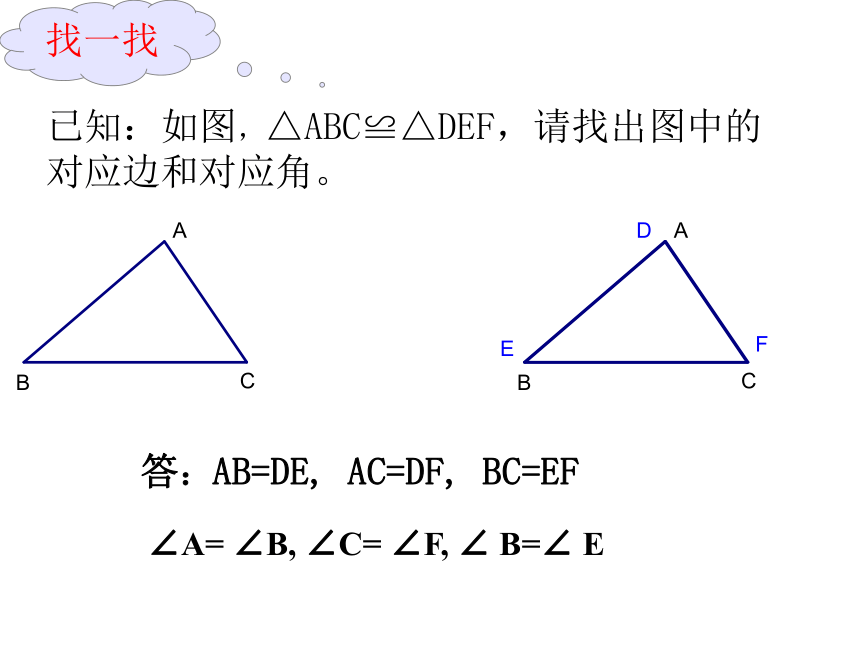
课件26张PPT。探索三角形全等的条件(1)已知：如图，△ABC≌△DEF，请找出图中的对应边和对应角。答：AB=DE, AC=DF, BC=EF∠A= ∠B, ∠C= ∠F, ∠ B=∠ E找一找一：给出一个条件画三角形。1. 给出一条边长 3 cm动动手2. 给出一个角一：给出一个条件画三角形。1. 给出两条边。二：给出两个条件画三角形。2. 给出两个角二：给出两个条件画三角形。3. 给出一条边，一个角 只给出一个条件或两个条件时,
都不能保证所画出的三角形全等.结论:三：议一议若给出三个条件画三角形，你能说出有哪几中可能情况?都给角：给三个角
2. 都给边：给三条边3.既给角，又给边：给两条边，一个角给一条边，两个角（1）（2）已知一个三角形的三个内角 分别为400，600，800，请画出这个三角形。结论：三个内角对应相等的两个三角形不一定全等.1.给出三个角已知三角形的三条边分 别为4cm、5cm和7cm，
请画出这个三角形。三边对应相等的两个三角形全等，
简写为“边边边”或“SSS”边边边公理：2.给出三条边例1 如图，当 AB=CD，BC=DA时，图中的△ABC与△CDA是否全等？并说明理由。答:△ABC与△CDA是全等三角形。证明：在△ABC与△CDA中∴△ABC≌△CDA（SSS）∵AB=CDAD=CBAC=CA(已知)(已知)(公共边)四、例题赏析∴∠3=∠4， ∠1=∠2 (全等三角形对应角相等）答：能判定AB∥CD.
∴AB∥CD， AD∥BC （内错角相等，两直线平行）变式 如图，当 AB=CD，BC=DA时，你能说明AB与CD、AD与BC的位置关系吗？为什么？证明：在△ABC与△CDA中∴△ABC≌△CDA（SSS）∵AB=CDAD=CBAC=CA(已知)(已知)(公共边)1234举一反三两个锐角对应相等的两个直角三角形全
等吗?为什么?答：不一定全等比如右边的两图，满足上述条件，但不全等四. 2.已知：AC、BD相交于点O，且AB=DC，AC=DB，那么∠A=∠D吗？为什么？答： 我认为：∠A=∠D证明：在△ABC和△DCB中∵∴△ABC≌△DCB （SSS）∴∠A=∠D（全等三角形的对应角相等）你能说出以下图形的设计原理吗?四边形不具有稳定性三角形具有稳定性。结论(1)只给出一个条件或两个条件时,都不能保证两个三角形全等.(2)三个内角对应相等的两个三角形不一 定全等.(3)边边边公理:三边对应相等的两个三角形全等,简写为“边边边”或“SSS”.(4)三角形具有稳定性.五.感悟与反思通过这节课的学习活动你有哪些收获？
你还有什么想法吗？1. 如图，AB=AC, BD=CD, BH=CH. 图中有几组全等的三角形？它们全等的条件是什么？解: 在△ABH和△ACH中同理 △ABD≌△ACD
△DBH≌△DCH( SSS)∴△ABH≌△ACH∵六、达标检测2.已知：如图，AB=DE, BC=EF, AF=CD.
(1) △ABC与△DEF是否全等？并说明理由。
(2) 求证：∠A=∠D证明:( SSS)∴ ∠A=∠D(全等三角形的对应角相等)答：我认为：△ABC≌△DEF∵AF = DC（已知）∴AF+FC= DC+FC（等式的性质）在△ABC和△DEF中∵AB = DE（已知）BC = EF（已知）AC = DF（已证）∴△ABC≌△DEF即AC=DF1.已知：如图，在△ABC中，AB=AC，D为BC边的中点，连结AD。（1）试判断AD与BC的位置关系，并证明。（2）AD能否平分∠BAC。（3）请你用简短的语言小结这一结论。思考题答: (1）AD能平分∠BAC ；(2) AD⊥ BC 。证明：在△ABD和△ ACD中∵AB=ACBD=CDAD=AD(已知)(已知)(公共边)∴△ABD≌△ACD(SSS)1234∴∠1=∠2，∠3=∠4(全等三角形的对应角相等)∵∠3+∠4=180°∴∠3=∠4=90°（平角的定义）（等式的性质）即：AD平分∠BAC ，且 AD⊥ BC .2.已知：如图，A、D、B、C在同一直线上，AD=BC，AE=DF，BE=CF，那么△ABE≌△DCF吗？ ∠E与∠F有什么关系？并证明你的结论。你能说明BE与CF的位置关系吗？并证明你的结论。证明： ∵AD=BC(已知)∴ AD+BD=BC+BD (等式的性质)即AB=DC在△ABE和△DCF 中∵∴ △ABE≌△DCF（SSS）∴ （全等三角形的对应角相等）∠C=∠ABE（全等三角形的对应角相等）∴BE∥CF（同位角相等，两直线平行）3.已知：如图，AB=AD，BC=DE，AC=AE，BC交DE于点M、交AD于点N。求证：∠ 1 = ∠ 2 = ∠3. 证明:在△ABC和△DCB中∵AB=ADBC=DEAC=AE(已知)(已知)(已知)∴△ABC≌△ADE(SSS)∴∠BAC=∠DAE， ∠B=∠D(全等三角形的对应角相等)即∠ 1+∠ DAC=∠ 2+∠ DAC∴∠1=∠2(等式的性质)∵ ∠ 3+∠ DNM+ ∠D =180o，∠1+∠ BNA+ ∠ B=180o
（三角形的三个内角和定理）∴∠1=∠3（等量代换）即∠1=∠2= ∠3作业：《轻松30分》P73 再见