2022-2023学年华东师大版八年级数学下册17.1变量与函数课后练习(无答案)
文档属性
| 名称 | 2022-2023学年华东师大版八年级数学下册17.1变量与函数课后练习(无答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 189.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-24 00:00:00 | ||
图片预览




文档简介
17.1变量与函数课后练习
班级:________ 姓名:________
一、单选题(共 10 小题)
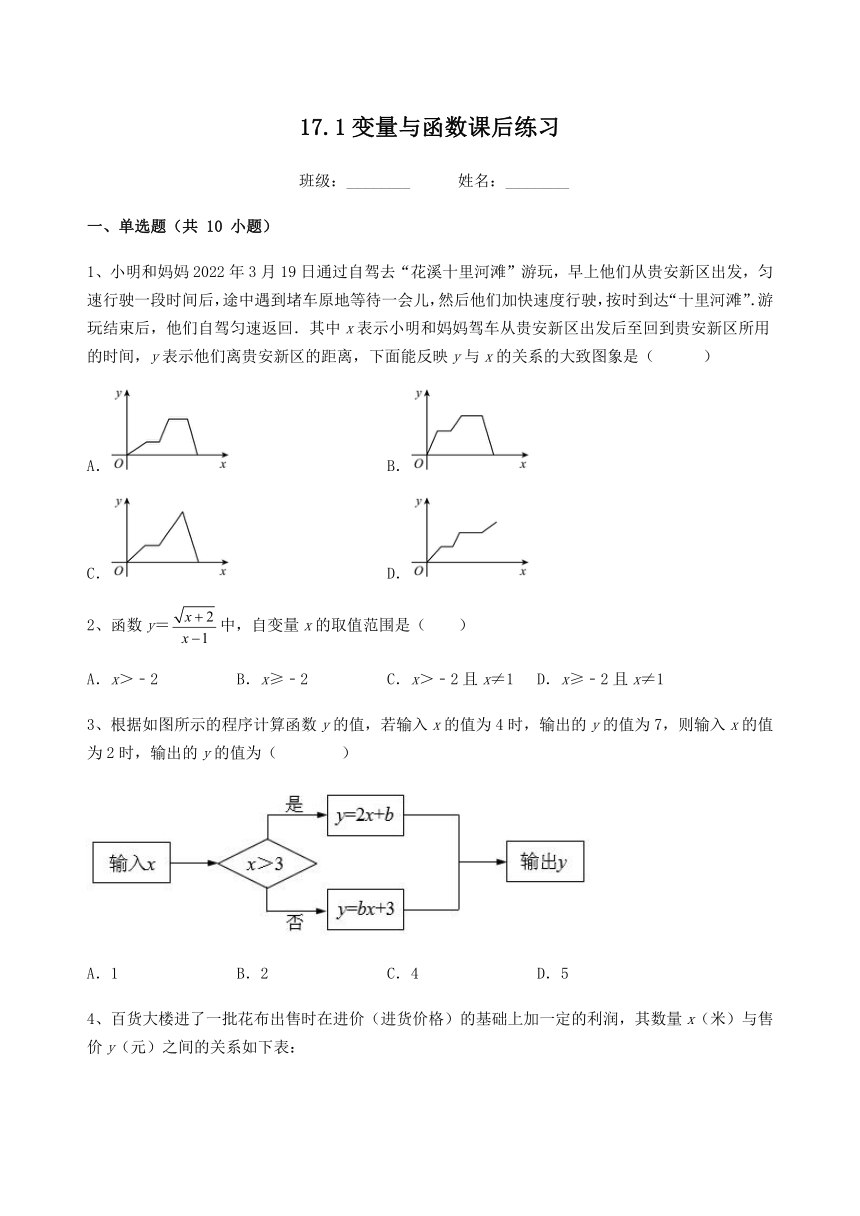
1、小明和妈妈2022年3月19日通过自驾去“花溪十里河滩”游玩,早上他们从贵安新区出发,匀速行驶一段时间后,途中遇到堵车原地等待一会儿,然后他们加快速度行驶,按时到达“十里河滩”.游玩结束后,他们自驾匀速返回.其中x表示小明和妈妈驾车从贵安新区出发后至回到贵安新区所用的时间,y表示他们离贵安新区的距离,下面能反映y与x的关系的大致图象是( )
A. B.
C. D.
2、函数y=中,自变量x的取值范围是( )
A.x>﹣2 B.x≥﹣2 C.x>﹣2且x≠1 D.x≥﹣2且x≠1
3、根据如图所示的程序计算函数y的值,若输入x的值为4时,输出的y的值为7,则输入x的值为2时,输出的y的值为( )
A.1 B.2 C.4 D.5
4、百货大楼进了一批花布出售时在进价(进货价格)的基础上加一定的利润,其数量x(米)与售价y(元)之间的关系如下表:
数量x(米) 2 3 4 5 …
售价y(元) …
下列用数量x表示售价y的关系中,正确的是( )
A. B. C. D.
5、弹簧挂上物体后会伸长,测得一弹簧的长度y(cm)与所挂的物体的重量x(kg)间有下面的关系:
x(kg) 0 1 2 3 4 5
y(cm) 10 10.5 11 11.5 12 12.5
下列说法不正确的是( )
与都是变量,且是自变量,是因变量
B.物体质量每增加1kg,弹簧长度增加0.5cm
C.所挂物体质量为7 kg时,弹簧长度为13.5 cm
D.与的关系表达式是
6、下列变量之间是函数关系的有( )
①正方形的面积S与边长a;
②长方形的周长C与长a;
③圆的周长C与半径R;
④中的y与x.
A.1个 B.2个 C.3个 D.4个
7、某地区用电量与应缴电费之间的关系如下表:则下列叙述错误的是( )
用电量(千瓦 时) 1 2 3 4 …
应缴电费(元) 0.55 1.10 1.65 2.20 …
A.用电量每增加1千瓦 时,电费增加0.55元
B.若用电量为8千瓦 时,则应缴电费4.4元
C.若应缴电费为2.75元,则用电量为6千瓦 时
D.应缴电费随用电量的增加而增加
8、某品牌热水壶的成本为50元,销售商对其销量与定价的关系进行了调查,结果如下:
定价/元 70 80 90 100 110 120
销量/把 80 100 110 100 80 60
现销售了把水壶,则定价约为( )
A.元 B.元 C.元 D.元
9、等腰三角形的周长是,腰长是底边长的函数,此函数解析式和自变量取值范围正确的是( )
A. B.
C. D.
10、已知一段导线的电阻R(Ω)与温度T(℃)的关系如下表,若导线的电阻R为4Ω,则导线的温度T为( )
温度T(℃) 0 1 2 3
电阻R(Ω) 2 2.08 2.16 2.24
A.25℃ B.30℃ C.40℃ D.50℃
二、填空题(共 8 小题)
1、已知函数,当时,y的值是______.
2、明星中学计划投资8万元购买学生用电脑,则所购电脑的台数n(台)与单价x(万元)之间的关系是_______________,其中________是常量,_______是变量.
3、将长为、宽为的长方形白纸,按如图所示的方法粘合起来,粘合部分的宽为,设张白纸粘合后的总长度为,与的函数关系式为___________.
4、汽车开始行驶时,油箱中有油30升,如果每小时耗油5升,那么油箱中的剩余油量(升)和工作时间(时)之间的函数关系式是____,自变量的取值范围____.
5、定义:给定关于x的函数y,对于该函数图象上任意两点(x1,y1),(x2,y2),当x1=﹣x2时,都有y1=y2,称该函数为偶函数,根据以上定义,可以判断下面所给的函数中,是偶函数的有__(填上所有正确答案的序号).
①y=2x; ②y=﹣x+1; ③y=x2; ④y=﹣;
6、向阳书店里某种书的定价元,如果购买本以上,超过本的部分打折.购书数量与付款金额之间的函数关系如下表所示:
购书数量(本) 1 2 3 4 5 6 7 8 9 10 11 …
应付金额(元) 10 20 30 40 50 60 70 80 88 96 104 …
则付款金额(元)关于购书数量(本)之间的函数关系用解析式表示是____________.
7、等边三角形的边长为x,此三角形的面积S表示成x的函数为______.
8、若函数,当自变量分别取1,2,,100时,对应的函数值的和是 __.
三、解答题(共 6 小题)
1、如图1,在中,于点D,,,动点E从点B出发,沿射线以的速度匀速运动,到达点D时停留1s后以原速度继续运动.如图2为的面积S()随时间t(s)的变化图像.
(1)填写图2中数据:________,_______,_______,_______;
(2)当_______s时,为的中线;
(3)当_______s时,;
(4)当动点E从点B出发时,动点F同时从点C沿边以的速度向终点B运动,当点F到达终点B后,点E也随之停止运动.当_______s时,.
2、某公交车每月的支出费用为4000元,每月的乘车人数x(人)与每月利润(利润=收入费用﹣支出费用)y(元)的变化关系如表所示(每位乘客的公交票价是固定不变的).
x(人) 500 1000 1500 2000 2500 3000 …
y(元) ﹣3000 ﹣2000 ﹣1000 0 1000 2000 …
(1)在这个变化过程中,每月的乘车人数x与每月利润y分别是 变量和 变量;
(2)观察表中数据可知,每月乘客量达到 人以上时,该公交车才不会亏损;
(3)当每月乘车人数为4000人时,每月利润为多少元?
3、一名高尔夫球手某次击出的球的高度h(m)和经过的水平距离d(m)满足下面的关系式:.
(1)当球经过的水平距离为50m时,球的高度是多少?
(2)当球第一次落到地面时,经过的水平距离是多少?
(3)设当球经过的水平距离分别为20m和80m时,球的高度分别为和,比较和的大小.
4、蜡烛厂为了解某批次蜡烛燃烧情况,进行了实验.点燃一根该批次蜡烛,蜡烛的高度h(cm)与燃烧的时间t(min)之间的关系如下表:
燃烧的时间t(min) 0 2 4 6 …
蜡烛的高度h(cm) 20 19 18 17 …
(1)上表反映了哪两个变量之间的关系?自变量、因变量各是什么?
(2)蜡烛的高度h(cm)与燃烧的时间t(min)之间的关系式是什么?
(3)若一根该批次蜡烛燃烧了26分钟,则此时这根蜡烛的高度是多少?
(4)若一根该批次蜡烛的高度为8厘米,则此时这根蜡烛已经燃烧的时间是多少?
5、如图,在一个边长为10cm的正方形的四个角处,都剪去一个大小相等的小正方形,当小正方形的边长由小到大变化时,图中阴影部分的面积也随之发生变化.
(1)在这个变化过程中,自变量、因变量各是什么?
(2)如果小正方形的边长为xcm,图中阴影部分的面积,请写出y与x之间的关系式;
(3)当小正方形的边长由1cm变化到2.5cm时,阴影部分的面积变小了多少?
6、某公交车每月的支出费用为4000元,每月的乘车人数x(人)与每月利润(利润=收入费用﹣支出费用)y(元)的变化关系如下表所示(每位乘客的公交票价是固定不变的):
x(人) 500 1000 1500 2000 2500 3000 …
y(元) ﹣3000 ﹣2000 ﹣1000 0 1000 2000 …
(1)在这个变化过程中,______是自变量,______是因变量;
(2)观察表中数据可知,每月乘客量达到_______人以上时,该公交车才不会亏损;
(3)请你估计当每月乘车人数为3500人时,每月利润为多少元?
班级:________ 姓名:________
一、单选题(共 10 小题)
1、小明和妈妈2022年3月19日通过自驾去“花溪十里河滩”游玩,早上他们从贵安新区出发,匀速行驶一段时间后,途中遇到堵车原地等待一会儿,然后他们加快速度行驶,按时到达“十里河滩”.游玩结束后,他们自驾匀速返回.其中x表示小明和妈妈驾车从贵安新区出发后至回到贵安新区所用的时间,y表示他们离贵安新区的距离,下面能反映y与x的关系的大致图象是( )
A. B.
C. D.
2、函数y=中,自变量x的取值范围是( )
A.x>﹣2 B.x≥﹣2 C.x>﹣2且x≠1 D.x≥﹣2且x≠1
3、根据如图所示的程序计算函数y的值,若输入x的值为4时,输出的y的值为7,则输入x的值为2时,输出的y的值为( )
A.1 B.2 C.4 D.5
4、百货大楼进了一批花布出售时在进价(进货价格)的基础上加一定的利润,其数量x(米)与售价y(元)之间的关系如下表:
数量x(米) 2 3 4 5 …
售价y(元) …
下列用数量x表示售价y的关系中,正确的是( )
A. B. C. D.
5、弹簧挂上物体后会伸长,测得一弹簧的长度y(cm)与所挂的物体的重量x(kg)间有下面的关系:
x(kg) 0 1 2 3 4 5
y(cm) 10 10.5 11 11.5 12 12.5
下列说法不正确的是( )
与都是变量,且是自变量,是因变量
B.物体质量每增加1kg,弹簧长度增加0.5cm
C.所挂物体质量为7 kg时,弹簧长度为13.5 cm
D.与的关系表达式是
6、下列变量之间是函数关系的有( )
①正方形的面积S与边长a;
②长方形的周长C与长a;
③圆的周长C与半径R;
④中的y与x.
A.1个 B.2个 C.3个 D.4个
7、某地区用电量与应缴电费之间的关系如下表:则下列叙述错误的是( )
用电量(千瓦 时) 1 2 3 4 …
应缴电费(元) 0.55 1.10 1.65 2.20 …
A.用电量每增加1千瓦 时,电费增加0.55元
B.若用电量为8千瓦 时,则应缴电费4.4元
C.若应缴电费为2.75元,则用电量为6千瓦 时
D.应缴电费随用电量的增加而增加
8、某品牌热水壶的成本为50元,销售商对其销量与定价的关系进行了调查,结果如下:
定价/元 70 80 90 100 110 120
销量/把 80 100 110 100 80 60
现销售了把水壶,则定价约为( )
A.元 B.元 C.元 D.元
9、等腰三角形的周长是,腰长是底边长的函数,此函数解析式和自变量取值范围正确的是( )
A. B.
C. D.
10、已知一段导线的电阻R(Ω)与温度T(℃)的关系如下表,若导线的电阻R为4Ω,则导线的温度T为( )
温度T(℃) 0 1 2 3
电阻R(Ω) 2 2.08 2.16 2.24
A.25℃ B.30℃ C.40℃ D.50℃
二、填空题(共 8 小题)
1、已知函数,当时,y的值是______.
2、明星中学计划投资8万元购买学生用电脑,则所购电脑的台数n(台)与单价x(万元)之间的关系是_______________,其中________是常量,_______是变量.
3、将长为、宽为的长方形白纸,按如图所示的方法粘合起来,粘合部分的宽为,设张白纸粘合后的总长度为,与的函数关系式为___________.
4、汽车开始行驶时,油箱中有油30升,如果每小时耗油5升,那么油箱中的剩余油量(升)和工作时间(时)之间的函数关系式是____,自变量的取值范围____.
5、定义:给定关于x的函数y,对于该函数图象上任意两点(x1,y1),(x2,y2),当x1=﹣x2时,都有y1=y2,称该函数为偶函数,根据以上定义,可以判断下面所给的函数中,是偶函数的有__(填上所有正确答案的序号).
①y=2x; ②y=﹣x+1; ③y=x2; ④y=﹣;
6、向阳书店里某种书的定价元,如果购买本以上,超过本的部分打折.购书数量与付款金额之间的函数关系如下表所示:
购书数量(本) 1 2 3 4 5 6 7 8 9 10 11 …
应付金额(元) 10 20 30 40 50 60 70 80 88 96 104 …
则付款金额(元)关于购书数量(本)之间的函数关系用解析式表示是____________.
7、等边三角形的边长为x,此三角形的面积S表示成x的函数为______.
8、若函数,当自变量分别取1,2,,100时,对应的函数值的和是 __.
三、解答题(共 6 小题)
1、如图1,在中,于点D,,,动点E从点B出发,沿射线以的速度匀速运动,到达点D时停留1s后以原速度继续运动.如图2为的面积S()随时间t(s)的变化图像.
(1)填写图2中数据:________,_______,_______,_______;
(2)当_______s时,为的中线;
(3)当_______s时,;
(4)当动点E从点B出发时,动点F同时从点C沿边以的速度向终点B运动,当点F到达终点B后,点E也随之停止运动.当_______s时,.
2、某公交车每月的支出费用为4000元,每月的乘车人数x(人)与每月利润(利润=收入费用﹣支出费用)y(元)的变化关系如表所示(每位乘客的公交票价是固定不变的).
x(人) 500 1000 1500 2000 2500 3000 …
y(元) ﹣3000 ﹣2000 ﹣1000 0 1000 2000 …
(1)在这个变化过程中,每月的乘车人数x与每月利润y分别是 变量和 变量;
(2)观察表中数据可知,每月乘客量达到 人以上时,该公交车才不会亏损;
(3)当每月乘车人数为4000人时,每月利润为多少元?
3、一名高尔夫球手某次击出的球的高度h(m)和经过的水平距离d(m)满足下面的关系式:.
(1)当球经过的水平距离为50m时,球的高度是多少?
(2)当球第一次落到地面时,经过的水平距离是多少?
(3)设当球经过的水平距离分别为20m和80m时,球的高度分别为和,比较和的大小.
4、蜡烛厂为了解某批次蜡烛燃烧情况,进行了实验.点燃一根该批次蜡烛,蜡烛的高度h(cm)与燃烧的时间t(min)之间的关系如下表:
燃烧的时间t(min) 0 2 4 6 …
蜡烛的高度h(cm) 20 19 18 17 …
(1)上表反映了哪两个变量之间的关系?自变量、因变量各是什么?
(2)蜡烛的高度h(cm)与燃烧的时间t(min)之间的关系式是什么?
(3)若一根该批次蜡烛燃烧了26分钟,则此时这根蜡烛的高度是多少?
(4)若一根该批次蜡烛的高度为8厘米,则此时这根蜡烛已经燃烧的时间是多少?
5、如图,在一个边长为10cm的正方形的四个角处,都剪去一个大小相等的小正方形,当小正方形的边长由小到大变化时,图中阴影部分的面积也随之发生变化.
(1)在这个变化过程中,自变量、因变量各是什么?
(2)如果小正方形的边长为xcm,图中阴影部分的面积,请写出y与x之间的关系式;
(3)当小正方形的边长由1cm变化到2.5cm时,阴影部分的面积变小了多少?
6、某公交车每月的支出费用为4000元,每月的乘车人数x(人)与每月利润(利润=收入费用﹣支出费用)y(元)的变化关系如下表所示(每位乘客的公交票价是固定不变的):
x(人) 500 1000 1500 2000 2500 3000 …
y(元) ﹣3000 ﹣2000 ﹣1000 0 1000 2000 …
(1)在这个变化过程中,______是自变量,______是因变量;
(2)观察表中数据可知,每月乘客量达到_______人以上时,该公交车才不会亏损;
(3)请你估计当每月乘车人数为3500人时,每月利润为多少元?
