2022-2023学年 京改版九年级数学下册23.3轴对称变换 同步练习(无答案)
文档属性
| 名称 | 2022-2023学年 京改版九年级数学下册23.3轴对称变换 同步练习(无答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 435.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-24 00:00:00 | ||
图片预览


文档简介
23.3轴对称变换同步练习
班级:________ 姓名:________
一、单选题(共 10 小题)
1、下列说法正确的是( ).
A.如果两个三角形全等,则它们必是关于某条直线成轴对称的图形
B.如果两个三角形关于某条直线成轴对称,那么它们是全等三角形
C.等腰三角形是关于一条边上的中线成轴对称的图形
D.所有的轴对称图形都只有一条对称轴
2、在平面直角坐标系中,点A的坐标为(-2,-3),点B的坐标为(3,-3),下列说法不正确的是( )
A.点A在第三象限 B.点B在第二、四象限的角平分线上
C.线段AB平行于x轴 D.点A与点B关于y轴对称
3、是点关于x轴的对称点.若一个正比例函数的图象经过点,则该函数的表达式为( )
A. B. C. D.
4、在平面直角坐标系中,点A(2,m)在直线y=﹣2x+1上,点A关于y轴的对称点B恰好落在直线y=kx+2上,则k的值为( )
A.2 B.2.5 C.﹣2 D.﹣3
5、若点A(1+m,1﹣n)与点B(﹣3,2)关于y轴对称,则m+n的值是( )
A.﹣5 B.﹣3 C.3 D.1
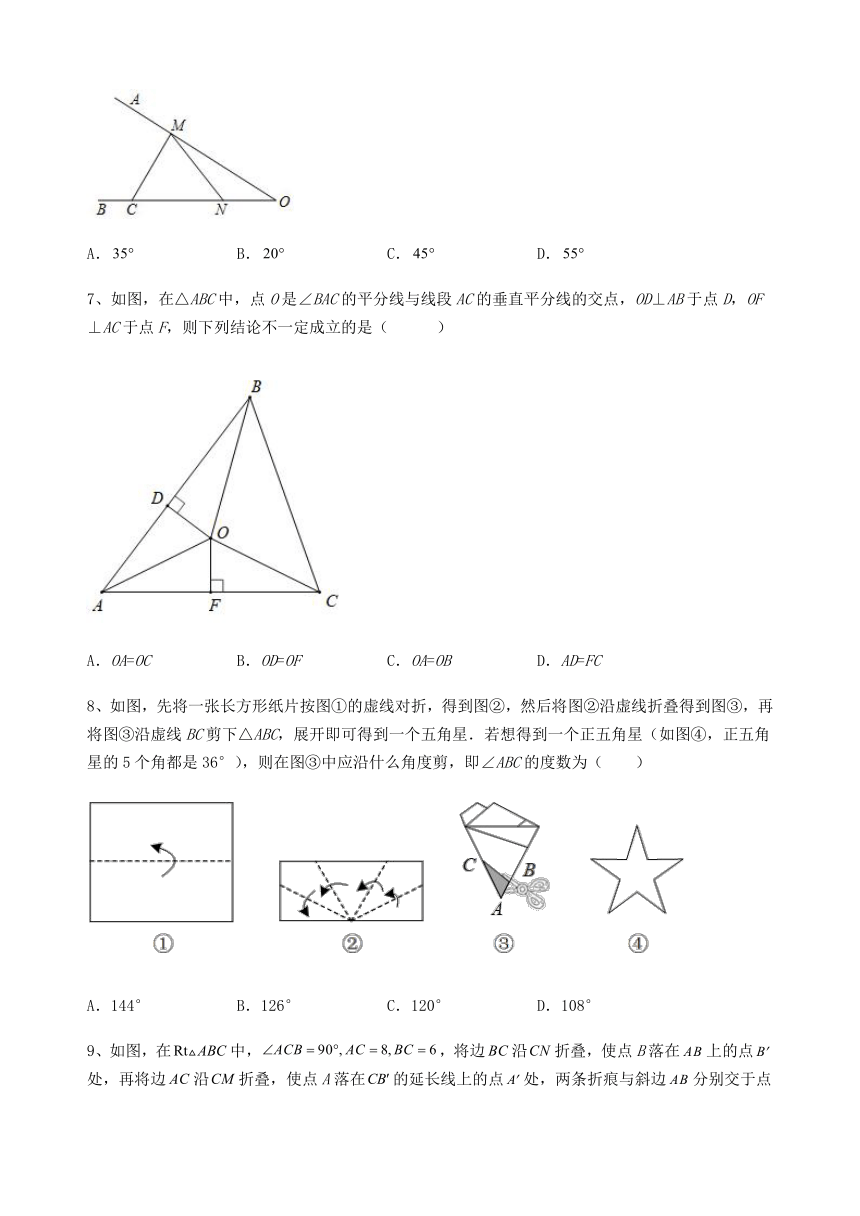
6、如图,,C为OB上的定点,M,N分别为射线OA、OB上的动点.当的值最小时,的度数为( )
A. B. C. D.
7、如图,在△ABC中,点O是∠BAC的平分线与线段AC的垂直平分线的交点,OD⊥AB于点D,OF⊥AC于点F,则下列结论不一定成立的是( )
A.OA=OC B.OD=OF C.OA=OB D.AD=FC
8、如图,先将一张长方形纸片按图①的虚线对折,得到图②,然后将图②沿虚线折叠得到图③,再将图③沿虚线BC剪下△ABC,展开即可得到一个五角星.若想得到一个正五角星(如图④,正五角星的5个角都是36°),则在图③中应沿什么角度剪,即∠ABC的度数为( )
A.144° B.126° C.120° D.108°
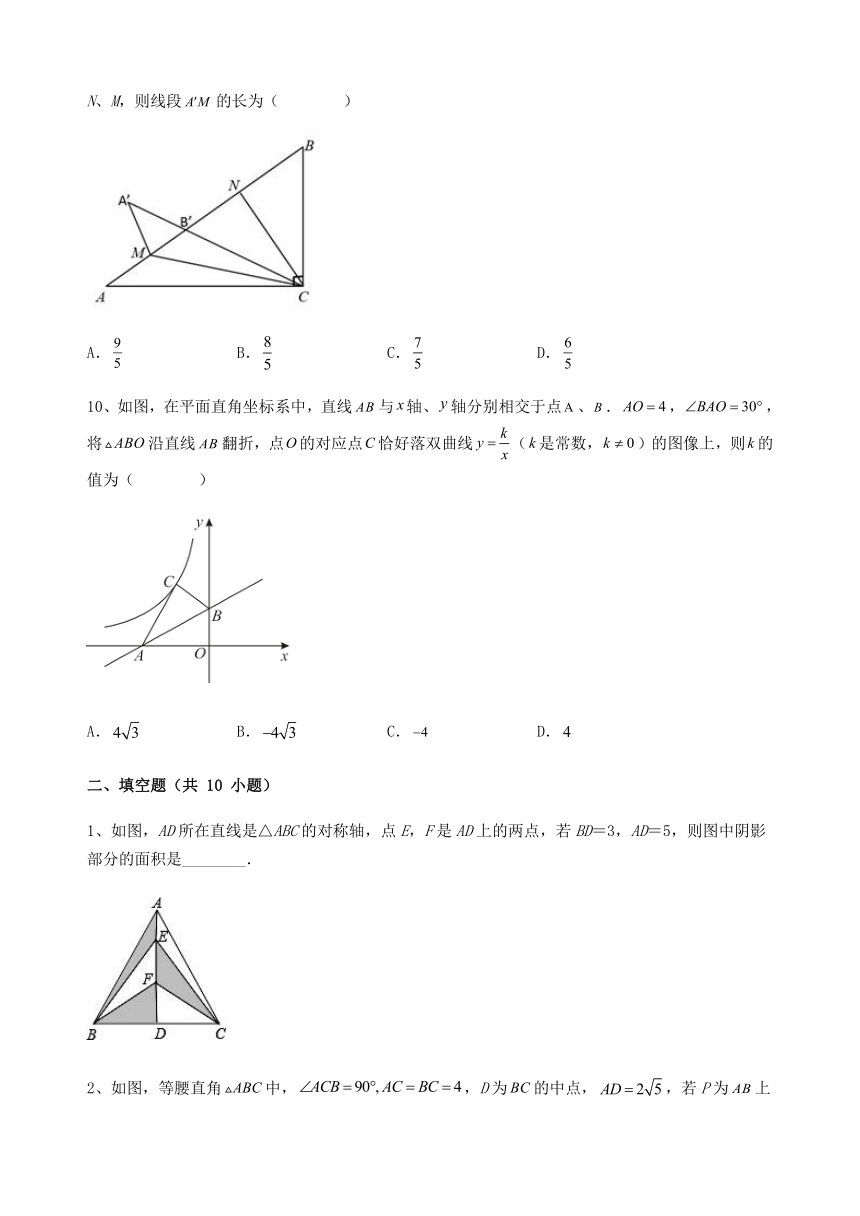
9、如图,在中,,将边沿折叠,使点B落在上的点处,再将边沿折叠,使点A落在的延长线上的点处,两条折痕与斜边分别交于点N、M,则线段的长为( )
A. B. C. D.
10、如图,在平面直角坐标系中,直线与轴、轴分别相交于点、.,,将沿直线翻折,点的对应点恰好落双曲线(是常数,)的图像上,则的值为( )
A. B. C. D.
二、填空题(共 10 小题)
1、如图,AD所在直线是△ABC的对称轴,点E,F是AD上的两点,若BD=3,AD=5,则图中阴影部分的面积是________.
2、如图,等腰直角中,,D为的中点,,若P为上一个动点,则的最小值为_________.
3、根据光学中平面镜光线反射原理,入射光线、反射光线与平面镜所夹的角相等.如图,是两面互相平行的平面镜,一束光线m通过镜面反射后的光线为n,再通过镜面β反射后的光线为k.光线m与镜面的夹角的度数为,光线n与光线k的夹角的度数为.则x与y之间的数量关系是______.
4、在平面直角坐标系中,的三个顶点分别为、、,如果以、、为顶点的三角形与全等(点与点不重合),请写出一个符合条件的点的坐标为________.
5、规定:两个函数,的图象关于y轴对称,则称这两个函数互为“Y函数”.例如:函数与的图象关于y轴对称,则这两个函数互为“Y函数”.若函数(k为常数)的“Y函数”图象与x轴只有一个交点,则其“Y函数”的解析式为______.
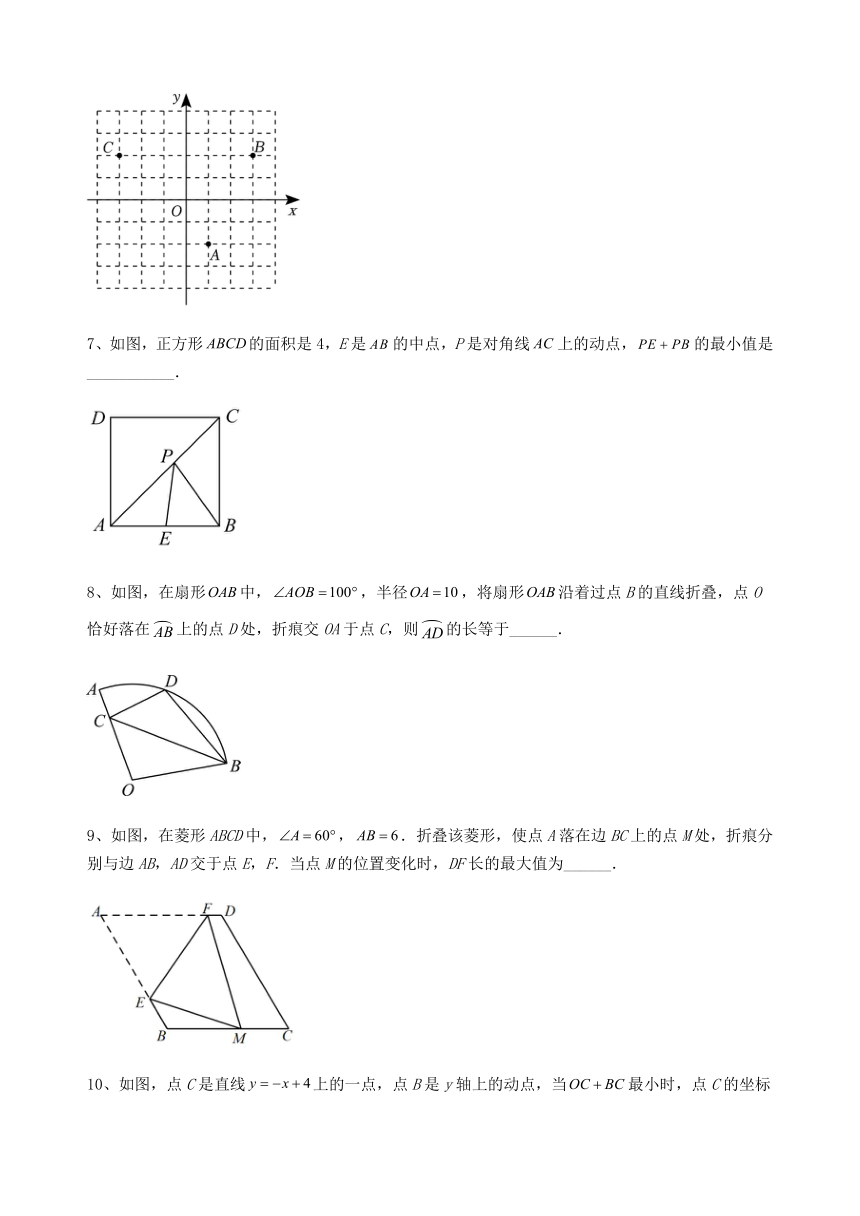
6、如图,在平面直角坐标系中,点A的坐标为(1,-2),点B的坐标为(3,2),点A与点C(-3,2)之间的距离为 _____,点D在y轴上运动,当AD+BD的值最小时,点D的坐标为 _____,此时AD+BD的最小值为 _____.
7、如图,正方形的面积是4,E是的中点,P是对角线上的动点,的最小值是___________.
8、如图,在扇形中,,半径,将扇形沿着过点B的直线折叠,点O恰好落在上的点D处,折痕交OA于点C,则的长等于______.
9、如图,在菱形ABCD中,,.折叠该菱形,使点A落在边BC上的点M处,折痕分别与边AB,AD交于点E,F.当点M的位置变化时,DF长的最大值为______.
10、如图,点C是直线上的一点,点B是y轴上的动点,当最小时,点C的坐标为______.
三、解答题(共 6 小题)
1、在平面直角坐标系中,的三个顶点的位置如图所示.
(1)请画出关于轴对称的;
(2)直接写出关于轴对称的的,,三点的坐标:__________,__________,__________;
(3)求的面积.
2、如图,长方形,点E是上的一点,将沿折叠后得到,且点O在长方形内部.已知,.
(1)如图1,若,求四边形的面积.
(2)如图2,延长交于F,连结,将沿折叠,当点D的对称点恰好为点O时,求四边形的面积.
(3)如图3,在(2)的条件下,延长交于点G,连结,将沿折叠,当点C的对称点恰好为点O时,求四边形的面积.
3、已知点A(﹣1,3a﹣1)与点B(2b+1,﹣2)关于x轴对称,点C(a+2,b)与点D关于原点对称.
(1)求点A、B、C、D的坐标;
(2)顺次联结点A、D、B、C,求所得图形的面积.
4、已知一次函数的图象与x轴,y轴交于点A、B.
(1)若将此函数图象沿x轴向右平移2个单位后经过原点,求b的值;
(2)若函数图象与一次函数的图象关于y轴对称,求k、b的值.
5、(1)如图1,已知△ABC为直角三角形,∠C=90°,若沿图中虚线剪去∠C,则∠1+∠2等于___________
A.90° B.135° C.270° D.315°
(2)如图2,已知△ABC中,∠A=40°,剪去∠A后成四边形,则∠1+∠2=_______
(3)如图2,根据(1)与(2)的求解过程,请你归纳猜想∠1+∠2与∠A的关系是________________
(4)如图3,若没有剪掉,而是把它折成如图3形状,试探究∠1+∠2与∠A的关系并说明理由.
6、如图,在直角坐标平面内,已知点A的坐标(﹣2,0).
(1)图中点B的坐标是______;
(2)点B关于原点对称的点C的坐标是_____;点A关于y轴对称的点D的坐标是______;
(3)四边形ABDC的面积是______;
(4)在y轴上找一点F,使,那么点F的所有可能位置是______.
班级:________ 姓名:________
一、单选题(共 10 小题)
1、下列说法正确的是( ).
A.如果两个三角形全等,则它们必是关于某条直线成轴对称的图形
B.如果两个三角形关于某条直线成轴对称,那么它们是全等三角形
C.等腰三角形是关于一条边上的中线成轴对称的图形
D.所有的轴对称图形都只有一条对称轴
2、在平面直角坐标系中,点A的坐标为(-2,-3),点B的坐标为(3,-3),下列说法不正确的是( )
A.点A在第三象限 B.点B在第二、四象限的角平分线上
C.线段AB平行于x轴 D.点A与点B关于y轴对称
3、是点关于x轴的对称点.若一个正比例函数的图象经过点,则该函数的表达式为( )
A. B. C. D.
4、在平面直角坐标系中,点A(2,m)在直线y=﹣2x+1上,点A关于y轴的对称点B恰好落在直线y=kx+2上,则k的值为( )
A.2 B.2.5 C.﹣2 D.﹣3
5、若点A(1+m,1﹣n)与点B(﹣3,2)关于y轴对称,则m+n的值是( )
A.﹣5 B.﹣3 C.3 D.1
6、如图,,C为OB上的定点,M,N分别为射线OA、OB上的动点.当的值最小时,的度数为( )
A. B. C. D.
7、如图,在△ABC中,点O是∠BAC的平分线与线段AC的垂直平分线的交点,OD⊥AB于点D,OF⊥AC于点F,则下列结论不一定成立的是( )
A.OA=OC B.OD=OF C.OA=OB D.AD=FC
8、如图,先将一张长方形纸片按图①的虚线对折,得到图②,然后将图②沿虚线折叠得到图③,再将图③沿虚线BC剪下△ABC,展开即可得到一个五角星.若想得到一个正五角星(如图④,正五角星的5个角都是36°),则在图③中应沿什么角度剪,即∠ABC的度数为( )
A.144° B.126° C.120° D.108°
9、如图,在中,,将边沿折叠,使点B落在上的点处,再将边沿折叠,使点A落在的延长线上的点处,两条折痕与斜边分别交于点N、M,则线段的长为( )
A. B. C. D.
10、如图,在平面直角坐标系中,直线与轴、轴分别相交于点、.,,将沿直线翻折,点的对应点恰好落双曲线(是常数,)的图像上,则的值为( )
A. B. C. D.
二、填空题(共 10 小题)
1、如图,AD所在直线是△ABC的对称轴,点E,F是AD上的两点,若BD=3,AD=5,则图中阴影部分的面积是________.
2、如图,等腰直角中,,D为的中点,,若P为上一个动点,则的最小值为_________.
3、根据光学中平面镜光线反射原理,入射光线、反射光线与平面镜所夹的角相等.如图,是两面互相平行的平面镜,一束光线m通过镜面反射后的光线为n,再通过镜面β反射后的光线为k.光线m与镜面的夹角的度数为,光线n与光线k的夹角的度数为.则x与y之间的数量关系是______.
4、在平面直角坐标系中,的三个顶点分别为、、,如果以、、为顶点的三角形与全等(点与点不重合),请写出一个符合条件的点的坐标为________.
5、规定:两个函数,的图象关于y轴对称,则称这两个函数互为“Y函数”.例如:函数与的图象关于y轴对称,则这两个函数互为“Y函数”.若函数(k为常数)的“Y函数”图象与x轴只有一个交点,则其“Y函数”的解析式为______.
6、如图,在平面直角坐标系中,点A的坐标为(1,-2),点B的坐标为(3,2),点A与点C(-3,2)之间的距离为 _____,点D在y轴上运动,当AD+BD的值最小时,点D的坐标为 _____,此时AD+BD的最小值为 _____.
7、如图,正方形的面积是4,E是的中点,P是对角线上的动点,的最小值是___________.
8、如图,在扇形中,,半径,将扇形沿着过点B的直线折叠,点O恰好落在上的点D处,折痕交OA于点C,则的长等于______.
9、如图,在菱形ABCD中,,.折叠该菱形,使点A落在边BC上的点M处,折痕分别与边AB,AD交于点E,F.当点M的位置变化时,DF长的最大值为______.
10、如图,点C是直线上的一点,点B是y轴上的动点,当最小时,点C的坐标为______.
三、解答题(共 6 小题)
1、在平面直角坐标系中,的三个顶点的位置如图所示.
(1)请画出关于轴对称的;
(2)直接写出关于轴对称的的,,三点的坐标:__________,__________,__________;
(3)求的面积.
2、如图,长方形,点E是上的一点,将沿折叠后得到,且点O在长方形内部.已知,.
(1)如图1,若,求四边形的面积.
(2)如图2,延长交于F,连结,将沿折叠,当点D的对称点恰好为点O时,求四边形的面积.
(3)如图3,在(2)的条件下,延长交于点G,连结,将沿折叠,当点C的对称点恰好为点O时,求四边形的面积.
3、已知点A(﹣1,3a﹣1)与点B(2b+1,﹣2)关于x轴对称,点C(a+2,b)与点D关于原点对称.
(1)求点A、B、C、D的坐标;
(2)顺次联结点A、D、B、C,求所得图形的面积.
4、已知一次函数的图象与x轴,y轴交于点A、B.
(1)若将此函数图象沿x轴向右平移2个单位后经过原点,求b的值;
(2)若函数图象与一次函数的图象关于y轴对称,求k、b的值.
5、(1)如图1,已知△ABC为直角三角形,∠C=90°,若沿图中虚线剪去∠C,则∠1+∠2等于___________
A.90° B.135° C.270° D.315°
(2)如图2,已知△ABC中,∠A=40°,剪去∠A后成四边形,则∠1+∠2=_______
(3)如图2,根据(1)与(2)的求解过程,请你归纳猜想∠1+∠2与∠A的关系是________________
(4)如图3,若没有剪掉,而是把它折成如图3形状,试探究∠1+∠2与∠A的关系并说明理由.
6、如图,在直角坐标平面内,已知点A的坐标(﹣2,0).
(1)图中点B的坐标是______;
(2)点B关于原点对称的点C的坐标是_____;点A关于y轴对称的点D的坐标是______;
(3)四边形ABDC的面积是______;
(4)在y轴上找一点F,使,那么点F的所有可能位置是______.
