人教版九年级下册27.1 图形的相似 提升卷(无答案)
文档属性
| 名称 | 人教版九年级下册27.1 图形的相似 提升卷(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 156.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-24 20:09:05 | ||
图片预览

文档简介
27.1 图形的相似
选择题
1.已知,那么下列等式中成立的是( )
A. B. C. D..
2.下列图形一定是相似图形的是( )
A.两个矩形
B.两个周长相等的直角三角形
C.两个正方形
D.两个等腰三角形
3.下列说法正确的是( )
A.对应边都成比例的多边形相似
B.对应角都相等的多边形相似
C.边数相同的正多边形相似
D.矩形都相似
4.若两个相似多边形的面积之比为4:9,则这两个多边形的周长之比为( )
A.: B.2:3 C.4:9 D.16:81
5.一个四边形各边长为2,3,4,5,另一个和它相似的四边形最长边为15,则的最短边长为( )
A.2 B.4 C.6 D.8
6.下列图形一定是相似图形的是( )
A.两个矩形
B.两个周长相等的直角三角形
C.两个正方形
D.两个等腰三角形
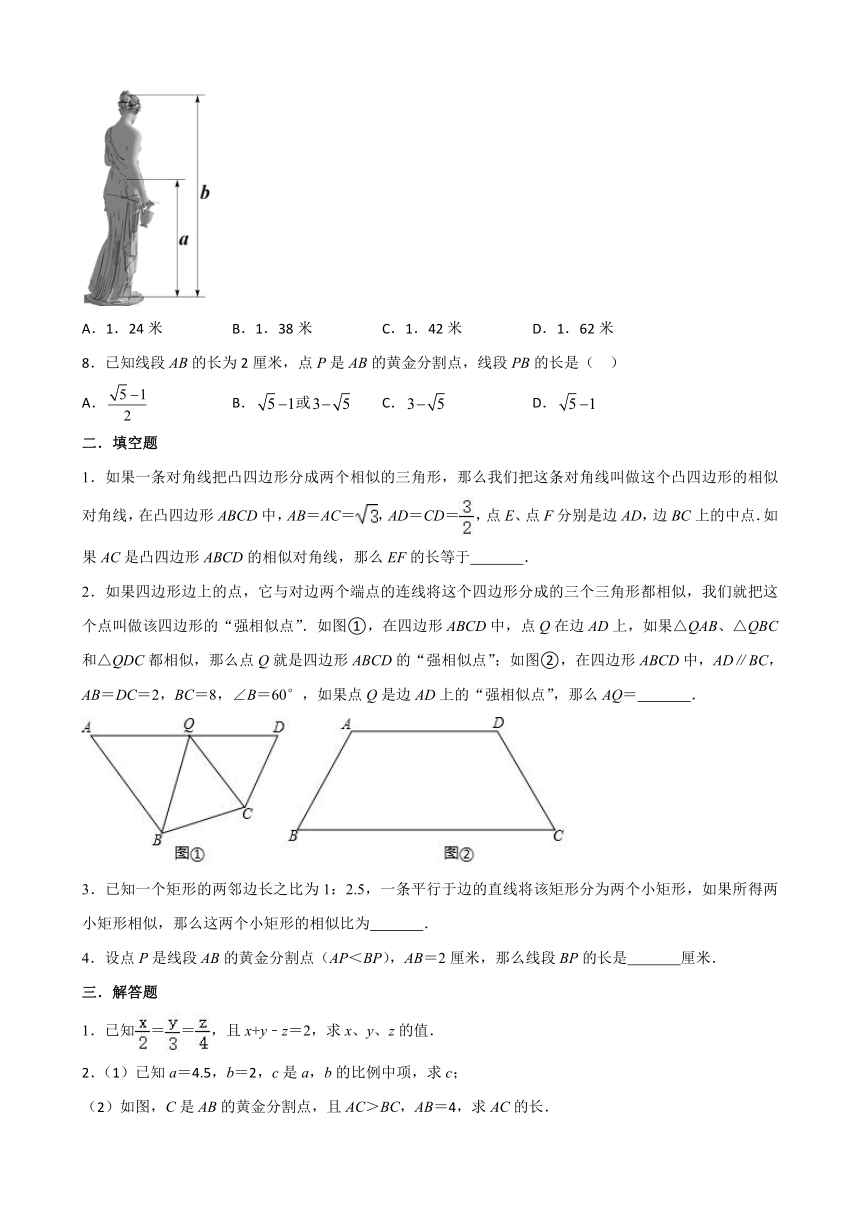
7.生活中到处可见黄金分割的美,如图,在设计人体雕像时,使雕像的腰部以下与全身的高度比值接近0.618,可以增加视觉美感,若图中为2米,则约为( )
A.1.24米 B.1.38米 C.1.42米 D.1.62米
8.已知线段AB的长为2厘米,点P是AB的黄金分割点,线段PB的长是( )
A. B.或 C. D.
填空题
1.如果一条对角线把凸四边形分成两个相似的三角形,那么我们把这条对角线叫做这个凸四边形的相似对角线,在凸四边形ABCD中,AB=AC=,AD=CD=,点E、点F分别是边AD,边BC上的中点.如果AC是凸四边形ABCD的相似对角线,那么EF的长等于 .
2.如果四边形边上的点,它与对边两个端点的连线将这个四边形分成的三个三角形都相似,我们就把这个点叫做该四边形的“强相似点”.如图①,在四边形ABCD中,点Q在边AD上,如果△QAB、△QBC和△QDC都相似,那么点Q就是四边形ABCD的“强相似点”;如图②,在四边形ABCD中,AD∥BC,AB=DC=2,BC=8,∠B=60°,如果点Q是边AD上的“强相似点”,那么AQ= .
3.已知一个矩形的两邻边长之比为1:2.5,一条平行于边的直线将该矩形分为两个小矩形,如果所得两小矩形相似,那么这两个小矩形的相似比为 .
4.设点P是线段AB的黄金分割点(AP<BP),AB=2厘米,那么线段BP的长是 厘米.
三.解答题
1.已知==,且x+y﹣z=2,求x、y、z的值.
2.(1)已知a=4.5,b=2,c是a,b的比例中项,求c;
(2)如图,C是AB的黄金分割点,且AC>BC,AB=4,求AC的长.
3.已知线段a、b满足a:b=3:2,且a+2b=28
(1)求a、b的值.
(2)若线段x是线段a、b的比例中项,求x的值.
4.如图是由小正方形组成的网格,每个小正方形的顶点叫做格点.的三个顶点都是格点.仅用无刻度的直尺在给定网格中完成画图,画图过程用虚线表示.
(1)在图(1)中,,分别是边,与网格线的交点.先将点绕点旋转得到点,画出点,再在上画点,使;
(2)在图(2)中,是边上一点,.先将绕点逆时针旋转,得到线段,画出线段,再画点,使,两点关于直线对称.
5.某校九年级数学兴趣小组在探究相似多边形问题时,他们提出了下面两个观点:
观点一:将外面大三角形按图1的方式向内缩小,得到新三角形,它们对应的边间距都为1,则新三角形与原三角形相似.
观点二:将邻边为6和10的矩形按图2的方式向内缩小,得到新的矩形,它们对应的边间距都为1,则新矩形与原矩形相似.
请回答下列问题:
(1)你认为上述两个观点是否正确?请说明理由.
(2)如图3,已知△ABC,AC=6,BC=8,AB=10,将△ABC按图3的方式向外扩张,得到△DEF,它们对应的边间距都为1,DE=15,求△DEF的面积.
选择题
1.已知,那么下列等式中成立的是( )
A. B. C. D..
2.下列图形一定是相似图形的是( )
A.两个矩形
B.两个周长相等的直角三角形
C.两个正方形
D.两个等腰三角形
3.下列说法正确的是( )
A.对应边都成比例的多边形相似
B.对应角都相等的多边形相似
C.边数相同的正多边形相似
D.矩形都相似
4.若两个相似多边形的面积之比为4:9,则这两个多边形的周长之比为( )
A.: B.2:3 C.4:9 D.16:81
5.一个四边形各边长为2,3,4,5,另一个和它相似的四边形最长边为15,则的最短边长为( )
A.2 B.4 C.6 D.8
6.下列图形一定是相似图形的是( )
A.两个矩形
B.两个周长相等的直角三角形
C.两个正方形
D.两个等腰三角形
7.生活中到处可见黄金分割的美,如图,在设计人体雕像时,使雕像的腰部以下与全身的高度比值接近0.618,可以增加视觉美感,若图中为2米,则约为( )
A.1.24米 B.1.38米 C.1.42米 D.1.62米
8.已知线段AB的长为2厘米,点P是AB的黄金分割点,线段PB的长是( )
A. B.或 C. D.
填空题
1.如果一条对角线把凸四边形分成两个相似的三角形,那么我们把这条对角线叫做这个凸四边形的相似对角线,在凸四边形ABCD中,AB=AC=,AD=CD=,点E、点F分别是边AD,边BC上的中点.如果AC是凸四边形ABCD的相似对角线,那么EF的长等于 .
2.如果四边形边上的点,它与对边两个端点的连线将这个四边形分成的三个三角形都相似,我们就把这个点叫做该四边形的“强相似点”.如图①,在四边形ABCD中,点Q在边AD上,如果△QAB、△QBC和△QDC都相似,那么点Q就是四边形ABCD的“强相似点”;如图②,在四边形ABCD中,AD∥BC,AB=DC=2,BC=8,∠B=60°,如果点Q是边AD上的“强相似点”,那么AQ= .
3.已知一个矩形的两邻边长之比为1:2.5,一条平行于边的直线将该矩形分为两个小矩形,如果所得两小矩形相似,那么这两个小矩形的相似比为 .
4.设点P是线段AB的黄金分割点(AP<BP),AB=2厘米,那么线段BP的长是 厘米.
三.解答题
1.已知==,且x+y﹣z=2,求x、y、z的值.
2.(1)已知a=4.5,b=2,c是a,b的比例中项,求c;
(2)如图,C是AB的黄金分割点,且AC>BC,AB=4,求AC的长.
3.已知线段a、b满足a:b=3:2,且a+2b=28
(1)求a、b的值.
(2)若线段x是线段a、b的比例中项,求x的值.
4.如图是由小正方形组成的网格,每个小正方形的顶点叫做格点.的三个顶点都是格点.仅用无刻度的直尺在给定网格中完成画图,画图过程用虚线表示.
(1)在图(1)中,,分别是边,与网格线的交点.先将点绕点旋转得到点,画出点,再在上画点,使;
(2)在图(2)中,是边上一点,.先将绕点逆时针旋转,得到线段,画出线段,再画点,使,两点关于直线对称.
5.某校九年级数学兴趣小组在探究相似多边形问题时,他们提出了下面两个观点:
观点一:将外面大三角形按图1的方式向内缩小,得到新三角形,它们对应的边间距都为1,则新三角形与原三角形相似.
观点二:将邻边为6和10的矩形按图2的方式向内缩小,得到新的矩形,它们对应的边间距都为1,则新矩形与原矩形相似.
请回答下列问题:
(1)你认为上述两个观点是否正确?请说明理由.
(2)如图3,已知△ABC,AC=6,BC=8,AB=10,将△ABC按图3的方式向外扩张,得到△DEF,它们对应的边间距都为1,DE=15,求△DEF的面积.
