人教版七年级数学下册5.1相交线(基础训练)(含答案)
文档属性
| 名称 | 人教版七年级数学下册5.1相交线(基础训练)(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 373.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-24 00:00:00 | ||
图片预览




文档简介
5.1相交线
(基础训练)
一、单选题
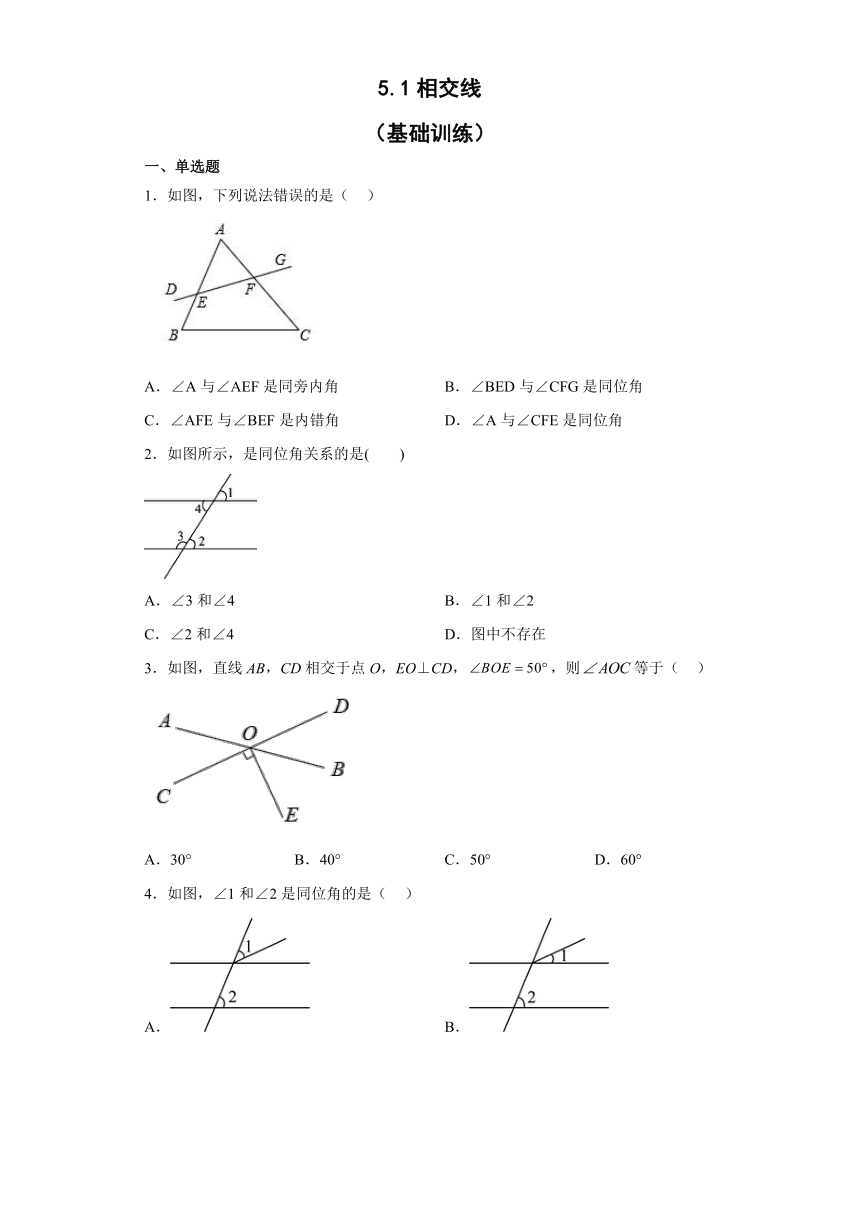
1.如图,下列说法错误的是( )
A.∠A与∠AEF是同旁内角 B.∠BED与∠CFG是同位角
C.∠AFE与∠BEF是内错角 D.∠A与∠CFE是同位角
2.如图所示,是同位角关系的是( )
A.∠3和∠4 B.∠1和∠2
C.∠2和∠4 D.图中不存在
3.如图,直线AB,CD相交于点O,EO⊥CD,,则等于( )
A.30° B.40° C.50° D.60°
4.如图,∠1和∠2是同位角的是( )
A. B.
C. D.
5.如图,下列结论中错误的是( )
A.与是同位角 B.与是内错角
C.与是同旁内角 D.与是对顶角
6.下列各图中,∠1与∠2是对顶角的是( )
A. B.
C. D.
7.如图,直线AB,CD相交于点O,OE平分.若,则的度数为( )
A. B. C. D.
8.如图,下列各组角中,是同位角的一组是( )
A.和 B.和
C.和 D.和
9.如图,直线,被直线和所截,则的同位角有( )个.
A.2 B.3 C.4 D.1
10.如图,直线AB经过点O,若OC⊥OD,∠1=32°,则∠2的大小是( )
A.78° B.68° C.58° D.32°
二、填空题
11.已知线段AB与直线CD互相垂直,垂足为点O,且AO=5 cm,BO=3 cm,则线段AB的长为______________.
12.如图,过直线AB上一点O作射线,,平分,则的度数为__________.
13.如图,某单位要在河岸上建一个水泵房引水到处,他们的做法是:过点作于点,将水泵房建在了处.这样做最节省水管长度,其数学道理是_______.
14.如图,,于点,cm,cm,cm,cm,cm,则点到直线的距离是__________cm.
15.已知∠AOB与∠BOC互为邻补角,OD平分∠BOC,OE⊥OB于点O,若∠AOD=4∠BOC,则∠DOE=_____.
三、解答题
16.如图,直线,相交于点,,是的平分线,是的反向延长线.
(1)求、的度数;
(2)说明平分的理由.
17.如图,直线,相交于点,平分.
(1)若,,求的度数;
(2)若平分,,设.
①求证;
②求的度数.
18.如图,直线与直线相交于点,是内一点,已知,平分,求的度数.
19.拓展题,如图所示,其中同旁内角有多少对?
20.如图,A为射线外一点.
(1)连接;
(2)过点A画出射线的垂线,垂足为点C;(可以使用各种数学工具)
(3)在线段的延长线上取点D,使得;
(4)画出射线;
(5)请直接写出上述所得图形中直角有______个.
21.如图所示,火车站,码头分别位于A,B两点,直线a,b分别表示铁路与河流.
(1)从火车站到码头怎样走最近?请画图并说明理由.
(2)从码头到铁路怎样走最近?请画图并说明理由.
参考答案:
1.B2.B3.B4.A5.B6.C7.C8.A9.B10.C
11.8 cm或2 cm.
12.
13.垂线段最短
14.
15.110°或70°
16.解(1)∵和互为补角,且
∴
∵是的平分线
∴
∵是的反向延长线
∴
(2)解:∵是的平分线,
∴
∵是的反向延长线,
∴,
∴
∴平分
17.(1)∵直线,相交于点,
∴∠BOD=∠AOC=70°,
∵平分,
∴∠BOE=∠DOE=35°,
又∵,
∴∠EOF=∠DOF-DOE=90°-35°=55°.
(2)①∵直线,相交于点,
∴∠BOC=∠AOD
又∵平分,
∴∠BOE=∠DOE,
∴∠BOC+∠BOE=∠AOD+∠DOE
即
②∵,,
∴∠COE=x°,
∴∠DOE=180°-x°
∵OE平分∠BOD
∴∠BOE=∠DOE=180°-x°
∵平分
∴∠COF=∠EOF=
∴∠BOF=∠EOF-∠BOE=
∵
即
解得:
∴∠COE=130°,∠BOE=∠DOE=180°-130°=50°,
∴∠AOC=∠BOD=2∠DOE=100°,
故∠AOC=100°.
18.
19.AD,EF被AB所截得的同旁内角是∠A与∠AEF;AD,EF被CD所截得的同旁内角是∠D与∠DFE;EF,BC被AB所截得的同旁内角是∠FEB与∠B;EF,BC被CD所截得的同旁内角是∠EFC与∠C;AB,CD被AD所截得的同旁内角是∠A与∠D;AB,CD被EF所截得的同旁内角是∠AEF与∠DFE,∠BEF与∠EFC;AB,CD被BC所截得的同旁内角是∠B与∠C;AD,BC被AB所截得的同旁内角是∠A与∠B;AD,BC被CD所截得的同旁内角是∠D与∠C,故同旁内角共有10对.
20.(1)解:连接,如图:
(2)解:如图:使用直角三角板,过点A画出射线的垂线,垂足为点C,
(3)解:如图:使用圆规在线段的延长线上取点D,使得,
(4)解:如图:使用直尺画出射线,
(5)解:图中的直角有:,,,,共有4个,
故答案为:4.
21.(1)如图,沿线段AB走,理由:两点之间,线段最短.
(2)如图,沿垂线段BD走,理由:垂线段最短.
(基础训练)
一、单选题
1.如图,下列说法错误的是( )
A.∠A与∠AEF是同旁内角 B.∠BED与∠CFG是同位角
C.∠AFE与∠BEF是内错角 D.∠A与∠CFE是同位角
2.如图所示,是同位角关系的是( )
A.∠3和∠4 B.∠1和∠2
C.∠2和∠4 D.图中不存在
3.如图,直线AB,CD相交于点O,EO⊥CD,,则等于( )
A.30° B.40° C.50° D.60°
4.如图,∠1和∠2是同位角的是( )
A. B.
C. D.
5.如图,下列结论中错误的是( )
A.与是同位角 B.与是内错角
C.与是同旁内角 D.与是对顶角
6.下列各图中,∠1与∠2是对顶角的是( )
A. B.
C. D.
7.如图,直线AB,CD相交于点O,OE平分.若,则的度数为( )
A. B. C. D.
8.如图,下列各组角中,是同位角的一组是( )
A.和 B.和
C.和 D.和
9.如图,直线,被直线和所截,则的同位角有( )个.
A.2 B.3 C.4 D.1
10.如图,直线AB经过点O,若OC⊥OD,∠1=32°,则∠2的大小是( )
A.78° B.68° C.58° D.32°
二、填空题
11.已知线段AB与直线CD互相垂直,垂足为点O,且AO=5 cm,BO=3 cm,则线段AB的长为______________.
12.如图,过直线AB上一点O作射线,,平分,则的度数为__________.
13.如图,某单位要在河岸上建一个水泵房引水到处,他们的做法是:过点作于点,将水泵房建在了处.这样做最节省水管长度,其数学道理是_______.
14.如图,,于点,cm,cm,cm,cm,cm,则点到直线的距离是__________cm.
15.已知∠AOB与∠BOC互为邻补角,OD平分∠BOC,OE⊥OB于点O,若∠AOD=4∠BOC,则∠DOE=_____.
三、解答题
16.如图,直线,相交于点,,是的平分线,是的反向延长线.
(1)求、的度数;
(2)说明平分的理由.
17.如图,直线,相交于点,平分.
(1)若,,求的度数;
(2)若平分,,设.
①求证;
②求的度数.
18.如图,直线与直线相交于点,是内一点,已知,平分,求的度数.
19.拓展题,如图所示,其中同旁内角有多少对?
20.如图,A为射线外一点.
(1)连接;
(2)过点A画出射线的垂线,垂足为点C;(可以使用各种数学工具)
(3)在线段的延长线上取点D,使得;
(4)画出射线;
(5)请直接写出上述所得图形中直角有______个.
21.如图所示,火车站,码头分别位于A,B两点,直线a,b分别表示铁路与河流.
(1)从火车站到码头怎样走最近?请画图并说明理由.
(2)从码头到铁路怎样走最近?请画图并说明理由.
参考答案:
1.B2.B3.B4.A5.B6.C7.C8.A9.B10.C
11.8 cm或2 cm.
12.
13.垂线段最短
14.
15.110°或70°
16.解(1)∵和互为补角,且
∴
∵是的平分线
∴
∵是的反向延长线
∴
(2)解:∵是的平分线,
∴
∵是的反向延长线,
∴,
∴
∴平分
17.(1)∵直线,相交于点,
∴∠BOD=∠AOC=70°,
∵平分,
∴∠BOE=∠DOE=35°,
又∵,
∴∠EOF=∠DOF-DOE=90°-35°=55°.
(2)①∵直线,相交于点,
∴∠BOC=∠AOD
又∵平分,
∴∠BOE=∠DOE,
∴∠BOC+∠BOE=∠AOD+∠DOE
即
②∵,,
∴∠COE=x°,
∴∠DOE=180°-x°
∵OE平分∠BOD
∴∠BOE=∠DOE=180°-x°
∵平分
∴∠COF=∠EOF=
∴∠BOF=∠EOF-∠BOE=
∵
即
解得:
∴∠COE=130°,∠BOE=∠DOE=180°-130°=50°,
∴∠AOC=∠BOD=2∠DOE=100°,
故∠AOC=100°.
18.
19.AD,EF被AB所截得的同旁内角是∠A与∠AEF;AD,EF被CD所截得的同旁内角是∠D与∠DFE;EF,BC被AB所截得的同旁内角是∠FEB与∠B;EF,BC被CD所截得的同旁内角是∠EFC与∠C;AB,CD被AD所截得的同旁内角是∠A与∠D;AB,CD被EF所截得的同旁内角是∠AEF与∠DFE,∠BEF与∠EFC;AB,CD被BC所截得的同旁内角是∠B与∠C;AD,BC被AB所截得的同旁内角是∠A与∠B;AD,BC被CD所截得的同旁内角是∠D与∠C,故同旁内角共有10对.
20.(1)解:连接,如图:
(2)解:如图:使用直角三角板,过点A画出射线的垂线,垂足为点C,
(3)解:如图:使用圆规在线段的延长线上取点D,使得,
(4)解:如图:使用直尺画出射线,
(5)解:图中的直角有:,,,,共有4个,
故答案为:4.
21.(1)如图,沿线段AB走,理由:两点之间,线段最短.
(2)如图,沿垂线段BD走,理由:垂线段最短.
