5.3平行线的性质(基础训练)(含答案)2022—2023学年人教版数学七年级下册
文档属性
| 名称 | 5.3平行线的性质(基础训练)(含答案)2022—2023学年人教版数学七年级下册 |
|
|
| 格式 | docx | ||
| 文件大小 | 249.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-24 00:00:00 | ||
图片预览

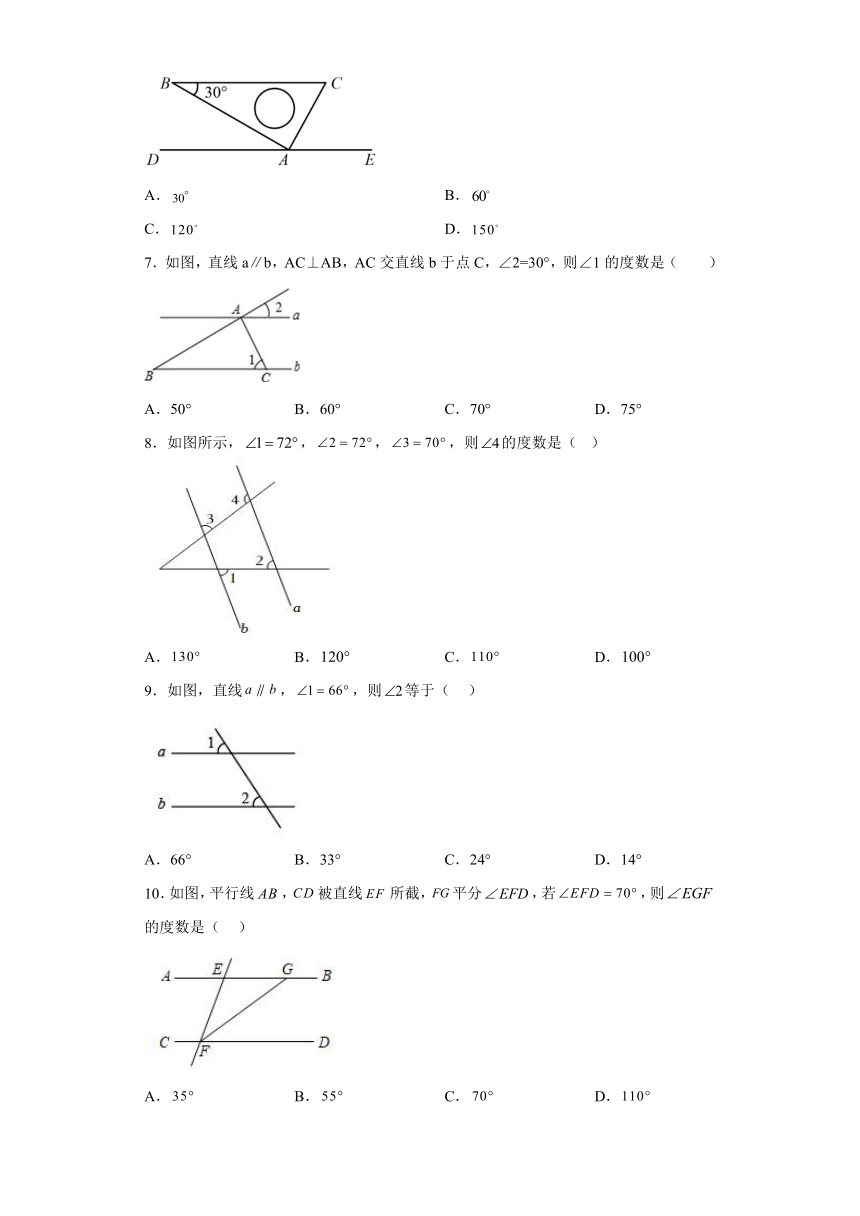
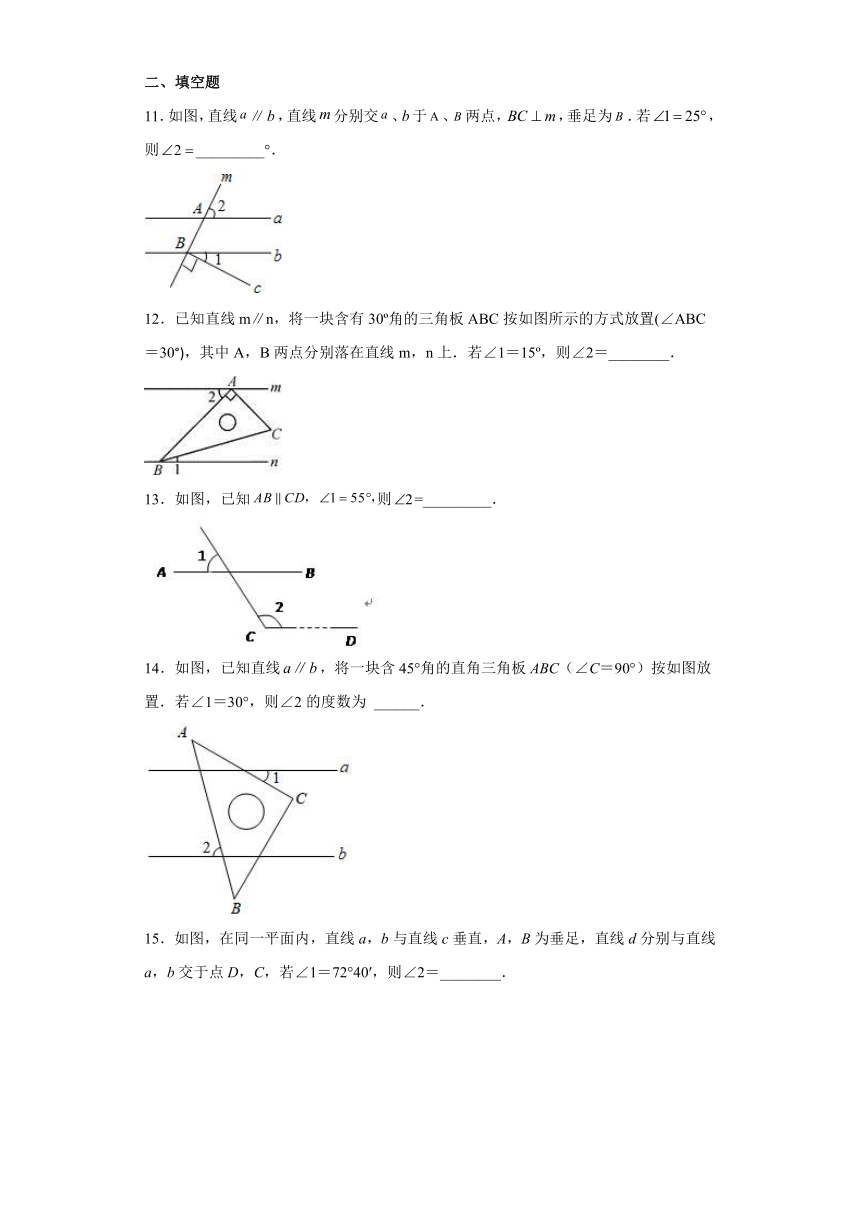
文档简介
5.3平行线的性质
(基础训练)
一、单选题
1.三角形中至少有
A.一个锐角 B.两个锐角
C.三个锐角 D.两个或三个锐角
2.如果∠α与∠β的两边分别平行,∠α比∠β的3倍少40°,则∠α的度数为( )
A.20° B.125° C.20°或125° D.35°或110°
3.将一副三角板和一个直尺按如图所示的位置摆放,则的度数为( )度.
A. B. C. D.
4.如图,AB∥CD,∠AEF=52°,FG平分∠EFD,则∠BGF的度数等于( )
A.154° B.152° C.136° D.144°
5.如图,直线,直线与直线,分别交于点,点,于点,交直线于点.如果,那么的度数为( )
A. B. C. D.
6.如图,将三角尺的直角顶点放在直线上,且使,则为( )
A. B.
C. D.
7.如图,直线a∥b,AC⊥AB,AC交直线b于点C,∠2=30°,则∠1的度数是( )
A.50° B.60° C.70° D.75°
8.如图所示,,,,则的度数是( )
A. B. C. D.
9.如图,直线,,则等于( )
A.66° B.33° C.24° D.14°
10.如图,平行线,被直线所截,平分,若,则的度数是( )
A. B. C. D.
二、填空题
11.如图,直线∥,直线分别交、于、两点,,垂足为.若,则_________°.
12.已知直线m∥n,将一块含有30 角的三角板ABC按如图所示的方式放置(∠ABC=30°),其中A,B两点分别落在直线m,n上.若∠1=15 ,则∠2=________.
13.如图,已知则=_________.
14.如图,已知直线,将一块含45°角的直角三角板ABC(∠C=90°)按如图放置.若∠1=30°,则∠2的度数为 ______.
15.如图,在同一平面内,直线a,b与直线c垂直,A,B为垂足,直线d分别与直线a,b交于点D,C,若∠1=72°40′,则∠2=________.
三、解答题
16.如图,已知AD⊥EF,CE⊥EF,∠2+∠3=180°.
(1)请说明∠1=∠BDC;
(2)若∠1=70°,DA平分∠BDC,试求∠FAB的度数.
17.完成下面的证明:如图,点、、分别是三角形的边,,上的点,//,.求证://.
证明:∵//(已知),
__________( ).
(已知),
___________(等量代换),
∴//( ).
18.如图,∠1=60°,∠2=60°,∠3=85°,求∠4的度数.
19.如图,在三角形ABC中,EF⊥AB,∠ADG=∠B,若点G在AC边上,∠1=∠2,判断CD与AB的位置关系,并说明理由.
20.如图,AB∥CD,AB平分∠EAD.求证:∠C=∠D.
参考答案:
1.B2.C3.C4.A5.B6.C7.B8.C9.A10.A
11.65
12.45°
13.
14.75°
15.107°20′
16.(1)∵AD⊥EF,CE⊥EF,
∴∠GAD=∠GEC=90°,
∴AD∥CE,
∴∠ADC+∠3=180°,
又∵∠2+∠3=180°,
∴∠2=∠ADC,
∴AB∥CD,
∴∠1=∠BDC;
(2) ∵AD⊥EF,
∴∠FAD=90°,
∵AB∥CD,
∴∠BDC=∠1=70°,
∵DA平分∠BDC,
∴∠ADC=∠BDC=×70°=35°,
∵AB∥CD,
∴∠2=∠ADC=35°,
∴∠FAB=∠FAD-∠2=90°-35°=55°.
17.或;两直线平行,同位角相等;或;内错角相等,两直线平行
18.∠4=85°.
19.解:CD⊥AB.理由如下:
∵∠ADG=∠B,
∴DG∥BC,
∴∠1=∠DCB,
∵∠1=∠2,
∴∠2=∠DCB,
∴CD∥EF,
∴∠CDB=∠EFB,
∵EF⊥AB,
∴∠EFB=90°,
∴∠CDB=90°,
∴CD⊥AB.
20.解:证明:∵AB∥CD,
∴∠BAD=∠D,∠EAB=∠C,
∵AB平分∠EAD,
∴∠EAB=∠BAD,
∴∠C=∠D.
(基础训练)
一、单选题
1.三角形中至少有
A.一个锐角 B.两个锐角
C.三个锐角 D.两个或三个锐角
2.如果∠α与∠β的两边分别平行,∠α比∠β的3倍少40°,则∠α的度数为( )
A.20° B.125° C.20°或125° D.35°或110°
3.将一副三角板和一个直尺按如图所示的位置摆放,则的度数为( )度.
A. B. C. D.
4.如图,AB∥CD,∠AEF=52°,FG平分∠EFD,则∠BGF的度数等于( )
A.154° B.152° C.136° D.144°
5.如图,直线,直线与直线,分别交于点,点,于点,交直线于点.如果,那么的度数为( )
A. B. C. D.
6.如图,将三角尺的直角顶点放在直线上,且使,则为( )
A. B.
C. D.
7.如图,直线a∥b,AC⊥AB,AC交直线b于点C,∠2=30°,则∠1的度数是( )
A.50° B.60° C.70° D.75°
8.如图所示,,,,则的度数是( )
A. B. C. D.
9.如图,直线,,则等于( )
A.66° B.33° C.24° D.14°
10.如图,平行线,被直线所截,平分,若,则的度数是( )
A. B. C. D.
二、填空题
11.如图,直线∥,直线分别交、于、两点,,垂足为.若,则_________°.
12.已知直线m∥n,将一块含有30 角的三角板ABC按如图所示的方式放置(∠ABC=30°),其中A,B两点分别落在直线m,n上.若∠1=15 ,则∠2=________.
13.如图,已知则=_________.
14.如图,已知直线,将一块含45°角的直角三角板ABC(∠C=90°)按如图放置.若∠1=30°,则∠2的度数为 ______.
15.如图,在同一平面内,直线a,b与直线c垂直,A,B为垂足,直线d分别与直线a,b交于点D,C,若∠1=72°40′,则∠2=________.
三、解答题
16.如图,已知AD⊥EF,CE⊥EF,∠2+∠3=180°.
(1)请说明∠1=∠BDC;
(2)若∠1=70°,DA平分∠BDC,试求∠FAB的度数.
17.完成下面的证明:如图,点、、分别是三角形的边,,上的点,//,.求证://.
证明:∵//(已知),
__________( ).
(已知),
___________(等量代换),
∴//( ).
18.如图,∠1=60°,∠2=60°,∠3=85°,求∠4的度数.
19.如图,在三角形ABC中,EF⊥AB,∠ADG=∠B,若点G在AC边上,∠1=∠2,判断CD与AB的位置关系,并说明理由.
20.如图,AB∥CD,AB平分∠EAD.求证:∠C=∠D.
参考答案:
1.B2.C3.C4.A5.B6.C7.B8.C9.A10.A
11.65
12.45°
13.
14.75°
15.107°20′
16.(1)∵AD⊥EF,CE⊥EF,
∴∠GAD=∠GEC=90°,
∴AD∥CE,
∴∠ADC+∠3=180°,
又∵∠2+∠3=180°,
∴∠2=∠ADC,
∴AB∥CD,
∴∠1=∠BDC;
(2) ∵AD⊥EF,
∴∠FAD=90°,
∵AB∥CD,
∴∠BDC=∠1=70°,
∵DA平分∠BDC,
∴∠ADC=∠BDC=×70°=35°,
∵AB∥CD,
∴∠2=∠ADC=35°,
∴∠FAB=∠FAD-∠2=90°-35°=55°.
17.或;两直线平行,同位角相等;或;内错角相等,两直线平行
18.∠4=85°.
19.解:CD⊥AB.理由如下:
∵∠ADG=∠B,
∴DG∥BC,
∴∠1=∠DCB,
∵∠1=∠2,
∴∠2=∠DCB,
∴CD∥EF,
∴∠CDB=∠EFB,
∵EF⊥AB,
∴∠EFB=90°,
∴∠CDB=90°,
∴CD⊥AB.
20.解:证明:∵AB∥CD,
∴∠BAD=∠D,∠EAB=∠C,
∵AB平分∠EAD,
∴∠EAB=∠BAD,
∴∠C=∠D.
