切线长定理及应用
图片预览

文档简介
遵义县中路片区
中小学交互式电子白板应用优质课比赛教案(初中数学)
执教人:冉瑞金(遵义县三岔中学)
教学时间 2013年11月21日 课题 切线长定理的应用 课型 习题课
学习内容分析 这节课是切线的性质、判定以及切线长定理初 ( http: / / www.21cnjy.com )步理解的学习基础上,进一步研究切线长定理的应用的有关知识和方法,本节课将在此基础上引导学生如何灵活应用切线长的定理以及三角形内切圆的有关知识。
学习者分析 本堂课是优质课比赛,由于学生对老师的不熟悉 ( http: / / www.21cnjy.com ),教学方法的不适应,可能会出现一些配合、语言沟通等方面的问题。所以首先要打破师生陌生的局面,其次在课堂上通过具体的问题的指引、学生自己思考、动手操作等,引发学生的兴趣,引导他们一步步达成了教学目标。
教学目标 课程标准:1、掌握切线长定理及其应用。
知识技能:1、在理解切线长定理的基础上熟练、灵活地应用切线长定理。2、掌握一些解题技巧和方法。
过程与方法:1、学生经历操作、观察、发现、探究、讨论、归纳、总结出切线长定理应用的过程,培养学生观察、比较、归纳的逻辑思维能力。2、学生经历探索、讨论求三角形内切圆和外切圆半径的过程,培养学生的概括能力和运用数学语言表述问题的能力。3、通过引导学生思考、解决问题,从而提炼相关的数学知识,渗透数形结合、一题多解的思想。
情感态度与价值观:1、学生经过观察、实验、 ( http: / / www.21cnjy.com )发现、探究、讨论、确认等数学活动,在探索切线长定理的应用过程中,体会在解决数学问题后的成功喜悦,感受解决数学的乐趣。2、掌握在平面几何中“无图无真相”的解题理念。
教学重点、难点及解决措施 教学重点:1、切线长定理的运用;2、掌握通过练习总结出的二级公式。教学难点:能熟练掌握并能灵活运用切线长定理解决数学问题。解决措施:利用课件,电子白板等,并创建活动让学生亲身参与,由此来引导学生对问题的思考,并逐步掌握解决问题的关键。
教学方法 观察讨论、合作交流、探究概括等
教学工具 多媒体、答题纸片
教学思路 本课的设计内容分为以下几个部分:1、认知准备,从情境导入,引导学生复习切线长定理。2、引导学生观察、探究、讨论、解决问题渗透解题技巧和方法。3、学生动手操作,能根据问题画出图形。从画图引入,激发学生的求知欲,从而得到其相关知识。4、巩固练习。5、引导学生小结本堂课的知识点。6、完成作业,教师质疑。
理论依据 引导发现式教学
信息技术应用分析 知识点 学 媒体内容与形式 使用方式、效果
切线长定理 能灵活运用切线长定理 计算机、电子白板、展台等 引起学生的兴趣,促使学生积极参与课堂活动,使他们由生动形象的感性知识逐步过渡到对知识的掌握
教学过程
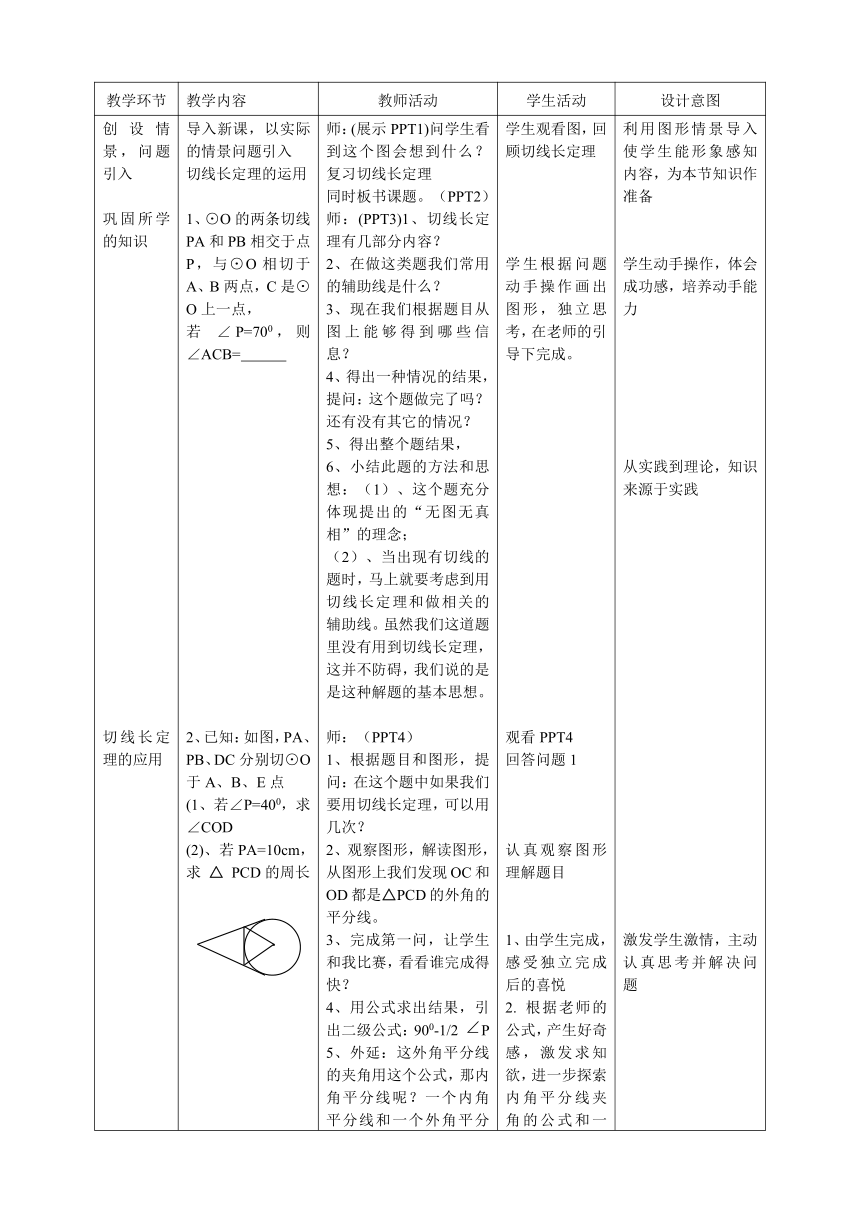
教学环节 教学内容 教师活动 学生活动 设计意图
创设情景,问题引入巩固所学的知识切线长定理的应用三角形内切圆的有关知识的应用。 应用迁移,巩固提高课堂作业课堂小结 导入新课,以实际的情景问题引入切线长定理的运用1、⊙O的两条切线PA和PB相交于点P,与⊙O相切于A、B两点,C是⊙O上一点,若 ∠P=700,则 ∠ACB= 2、已知:如图,PA、PB ( http: / / www.21cnjy.com )、DC分别切⊙O于A、B、E点
(1、若∠P=400,求 ∠COD
(2)、若PA=10cm,求 △ PCD的周长3、如图,⊙O是Rt△ABC的内切圆, ( http: / / www.21cnjy.com ) C=900
1、若AC=12cm,BC=9cm,求⊙O的半径
2、若BC=a,AC=b,AB=c,求⊙O的半径4、如图,AC⊥BC于点C,BC=a,CA=b,⊙O与直线AB、BC、CA都相切,则⊙O的半径等于 。练习1.如图,AB是⊙O的直径,AD、DC、BC是切线,点A、E、B为切点, (1)求证:OD ⊥ OC (2)若BC=9,AD=4,求OB的长.2、已知:P为⊙O外一点,PA、PB为⊙O的切线,A、B为切点,BC是直径。 求证:AC∥OP 师:(展示PPT1)问学生看到这个图会想到什么?复习切线长定理同时板书课题。(PPT2)师:(PPT3)1、切线长定理有几部分内容?2、在做这类题我们常用的辅助线是什么?3、现在我们根据题目从图上能够得到哪些信息?4、得出一种情况的结果,提问:这个题做完了吗?还有没有其它的情况?5、得出整个题结果,6、小结此题的方法和思想:(1)、这个题充分体现提出的“无图无真相”的理念;(2)、当出现有切线的题时,马上就 ( http: / / www.21cnjy.com )要考虑到用切线长定理和做相关的辅助线。虽然我们这道题里没有用到切线长定理,这并不防碍,我们说的是是这种解题的基本思想。师:(PPT4)1、根据题目和图形,提问:在这个题中如果我们要用切线长定理,可以用几次?2、观察图形,解读图形,从图形上我们发现OC和OD都是△PCD的外角的平分线。3、完成第一问,让学生和我比赛,看看谁完成得快?4、用公式求出结果,引出二级公式:900-1/2 P5、外延:这外角平分线的夹角用这个公式,那内角平分线呢?一个内角平分线和一个外角平分线的夹角呢?6、归纳:内角平分线夹角的关系:900+1/2∠x;一内角平分线和一外角平分线与它们不相邻的内角的关系:1/2∠x。师:(PPT5)1、解读图形,挑战自我,先一般再特殊,完成此题。先运用学习的切线长定理求出三角形内切圆的半径的公式。2、引导完成,做辅助线,连接OD、OE、OF,提问:根据图形,怎么做呀?从图上我们又能捕捉到些什么有用的信息呢?讲解此题。3、得出结论:直角三角形内切圆的半径公式r=(a+b-c)/2(切线长定理)提问:还有没有不同意见?引导学生讨论用面积法去完成。归纳:r=ab/(a+b+c),4、外延:提问:我们这是直角三角形内切圆的半径公式,那不是直角三角形的内切圆的半径又该咋办?(1)、能用切线长定理找关系吗?(2)、仍用面积法去求怎么样?师:(PPT6)1、观察图形,解读图的内容,有谁知道这个圆与△ABC有什么关系?2、引导得出旁切圆和旁心的概念。3、外延:提问:如果给你一个任意三角形,要找一个点与三角形三边的距离相等,这样的点有几个?4、根据上一题的方法,在此题中看能不能运用?5、根据切线长定理得出结论:r=(b+c-a)/2师:(PPT7)学习提醒,当在一个题中出现多条切线时,切线长定理是一个必用的定理。师:(PPT8)1、提问:要求证两条线垂直可用的方法有哪些?2、提问:通过对图形的观察,对此题你有什么思路?3、对于第二问提示:有什么方法建立数量关系?我们通常运用的方法是什么?看能不能运用勾股定理解决?4、发答题纸片,由学生完成,然后选做得好的同学的用展台进行展示,评讲师:(PPT9)由学生独立完成师:(PPT10)课堂小结切线长定理为证明线段相等,角相等,弧相等,垂直关系提供了理论依据。必须掌握并能灵活应用。2、希望同学们在以后的学习中要勇于探索和实践,养成科学的学习态度。同时还要注意总结作辅助线的方法和解题时要注意运用“数形结合”的思想方法。3、本堂课你学到些什么? 学生观看图,回顾切线长定理学生根据问题动手操作画出图形,独立思考,在老师的引导下完成。观看PPT4 回答问题1认真观察图形理解题目1、由学生完成,感受独立完成后的喜悦2. 根据老师的公式,产生好奇感,激发求知欲,进一步探索内角平分线夹角的公式和一个内角平分线和一外角平分线夹角的公式。学生思考,领会并记住公式,掌握解题技巧。学生认真观察图形掌握并能根据题目作出常用的辅助线,然后在图形中获取自己解题有用的信息。让学生感受一题多解的思想不同的思维方式可有不同的解题方法。让学生根据直角三角形内切圆半径的公式讨论一般三角形内切圆的半径公式认真观察图形,回答问题1掌握外延的相关知识知识的运用,根据上一题的讲解,掌握基本解题思路,及时运用到本题,得出结论通过学习提醒,提炼解题的基本思想,让学生掌握一定的解题思路。根据题目认真观察图形,首先打开解题思路,找到解题的方法,进行推理论证。积极讨论,发表意见然后在答题纸上开始答题,最先完成的,老师展台展示完成情况。学生口述切线长定理学生思考后发表意见,回答并总结 利用图形情景导入使学生能形象感知内容,为本节知识作准备学生动手操作,体会成功感,培养动手能力从实践到理论,知识来源于实践激发学生激情,主动认真思考并解决问题在探索过程中体验数学的快乐,把理论用于实践中去师生共同参与,培养了凝聚力激发学生的学习兴趣使学生养成观察、探索、探究、讨论、归纳的良好学习习惯,对知识的总结和积累培养学生的观察能力培养学生知识迁移的能力,灵活运用学过的解题方法得出结论,感受成功的喜悦。切线长定理的应用,在掌握基本解题思路和方法的同时,灵活的应用切线长定理解决数学问题。对学生独立完成作业后的肯定,激发学生独立完成作业的欲望,培养学生学习的自信心和成就感,养成良好的学习习惯。
板书设计 切线长定理切线长定理内容的两部分:一相等,二平分 关于三角形相关的角平分线的二级公式:900-1/2∠P,900+1/2∠x,1/2x直角三角形内切圆的半径公式r=(a+b-c)/2(切线长定理)直角三角形和一般三角形内切圆的半径公式:r=ab/(a+b+c)(面积法)
教学反思
.
O
D
E
C
B
A
P
F
E
D
C
B
A
O
.
C
B
A
O
.
O
A
B
C
D
E
C
P
A
B
D
O
A
中小学交互式电子白板应用优质课比赛教案(初中数学)
执教人:冉瑞金(遵义县三岔中学)
教学时间 2013年11月21日 课题 切线长定理的应用 课型 习题课
学习内容分析 这节课是切线的性质、判定以及切线长定理初 ( http: / / www.21cnjy.com )步理解的学习基础上,进一步研究切线长定理的应用的有关知识和方法,本节课将在此基础上引导学生如何灵活应用切线长的定理以及三角形内切圆的有关知识。
学习者分析 本堂课是优质课比赛,由于学生对老师的不熟悉 ( http: / / www.21cnjy.com ),教学方法的不适应,可能会出现一些配合、语言沟通等方面的问题。所以首先要打破师生陌生的局面,其次在课堂上通过具体的问题的指引、学生自己思考、动手操作等,引发学生的兴趣,引导他们一步步达成了教学目标。
教学目标 课程标准:1、掌握切线长定理及其应用。
知识技能:1、在理解切线长定理的基础上熟练、灵活地应用切线长定理。2、掌握一些解题技巧和方法。
过程与方法:1、学生经历操作、观察、发现、探究、讨论、归纳、总结出切线长定理应用的过程,培养学生观察、比较、归纳的逻辑思维能力。2、学生经历探索、讨论求三角形内切圆和外切圆半径的过程,培养学生的概括能力和运用数学语言表述问题的能力。3、通过引导学生思考、解决问题,从而提炼相关的数学知识,渗透数形结合、一题多解的思想。
情感态度与价值观:1、学生经过观察、实验、 ( http: / / www.21cnjy.com )发现、探究、讨论、确认等数学活动,在探索切线长定理的应用过程中,体会在解决数学问题后的成功喜悦,感受解决数学的乐趣。2、掌握在平面几何中“无图无真相”的解题理念。
教学重点、难点及解决措施 教学重点:1、切线长定理的运用;2、掌握通过练习总结出的二级公式。教学难点:能熟练掌握并能灵活运用切线长定理解决数学问题。解决措施:利用课件,电子白板等,并创建活动让学生亲身参与,由此来引导学生对问题的思考,并逐步掌握解决问题的关键。
教学方法 观察讨论、合作交流、探究概括等
教学工具 多媒体、答题纸片
教学思路 本课的设计内容分为以下几个部分:1、认知准备,从情境导入,引导学生复习切线长定理。2、引导学生观察、探究、讨论、解决问题渗透解题技巧和方法。3、学生动手操作,能根据问题画出图形。从画图引入,激发学生的求知欲,从而得到其相关知识。4、巩固练习。5、引导学生小结本堂课的知识点。6、完成作业,教师质疑。
理论依据 引导发现式教学
信息技术应用分析 知识点 学 媒体内容与形式 使用方式、效果
切线长定理 能灵活运用切线长定理 计算机、电子白板、展台等 引起学生的兴趣,促使学生积极参与课堂活动,使他们由生动形象的感性知识逐步过渡到对知识的掌握
教学过程
教学环节 教学内容 教师活动 学生活动 设计意图
创设情景,问题引入巩固所学的知识切线长定理的应用三角形内切圆的有关知识的应用。 应用迁移,巩固提高课堂作业课堂小结 导入新课,以实际的情景问题引入切线长定理的运用1、⊙O的两条切线PA和PB相交于点P,与⊙O相切于A、B两点,C是⊙O上一点,若 ∠P=700,则 ∠ACB= 2、已知:如图,PA、PB ( http: / / www.21cnjy.com )、DC分别切⊙O于A、B、E点
(1、若∠P=400,求 ∠COD
(2)、若PA=10cm,求 △ PCD的周长3、如图,⊙O是Rt△ABC的内切圆, ( http: / / www.21cnjy.com ) C=900
1、若AC=12cm,BC=9cm,求⊙O的半径
2、若BC=a,AC=b,AB=c,求⊙O的半径4、如图,AC⊥BC于点C,BC=a,CA=b,⊙O与直线AB、BC、CA都相切,则⊙O的半径等于 。练习1.如图,AB是⊙O的直径,AD、DC、BC是切线,点A、E、B为切点, (1)求证:OD ⊥ OC (2)若BC=9,AD=4,求OB的长.2、已知:P为⊙O外一点,PA、PB为⊙O的切线,A、B为切点,BC是直径。 求证:AC∥OP 师:(展示PPT1)问学生看到这个图会想到什么?复习切线长定理同时板书课题。(PPT2)师:(PPT3)1、切线长定理有几部分内容?2、在做这类题我们常用的辅助线是什么?3、现在我们根据题目从图上能够得到哪些信息?4、得出一种情况的结果,提问:这个题做完了吗?还有没有其它的情况?5、得出整个题结果,6、小结此题的方法和思想:(1)、这个题充分体现提出的“无图无真相”的理念;(2)、当出现有切线的题时,马上就 ( http: / / www.21cnjy.com )要考虑到用切线长定理和做相关的辅助线。虽然我们这道题里没有用到切线长定理,这并不防碍,我们说的是是这种解题的基本思想。师:(PPT4)1、根据题目和图形,提问:在这个题中如果我们要用切线长定理,可以用几次?2、观察图形,解读图形,从图形上我们发现OC和OD都是△PCD的外角的平分线。3、完成第一问,让学生和我比赛,看看谁完成得快?4、用公式求出结果,引出二级公式:900-1/2 P5、外延:这外角平分线的夹角用这个公式,那内角平分线呢?一个内角平分线和一个外角平分线的夹角呢?6、归纳:内角平分线夹角的关系:900+1/2∠x;一内角平分线和一外角平分线与它们不相邻的内角的关系:1/2∠x。师:(PPT5)1、解读图形,挑战自我,先一般再特殊,完成此题。先运用学习的切线长定理求出三角形内切圆的半径的公式。2、引导完成,做辅助线,连接OD、OE、OF,提问:根据图形,怎么做呀?从图上我们又能捕捉到些什么有用的信息呢?讲解此题。3、得出结论:直角三角形内切圆的半径公式r=(a+b-c)/2(切线长定理)提问:还有没有不同意见?引导学生讨论用面积法去完成。归纳:r=ab/(a+b+c),4、外延:提问:我们这是直角三角形内切圆的半径公式,那不是直角三角形的内切圆的半径又该咋办?(1)、能用切线长定理找关系吗?(2)、仍用面积法去求怎么样?师:(PPT6)1、观察图形,解读图的内容,有谁知道这个圆与△ABC有什么关系?2、引导得出旁切圆和旁心的概念。3、外延:提问:如果给你一个任意三角形,要找一个点与三角形三边的距离相等,这样的点有几个?4、根据上一题的方法,在此题中看能不能运用?5、根据切线长定理得出结论:r=(b+c-a)/2师:(PPT7)学习提醒,当在一个题中出现多条切线时,切线长定理是一个必用的定理。师:(PPT8)1、提问:要求证两条线垂直可用的方法有哪些?2、提问:通过对图形的观察,对此题你有什么思路?3、对于第二问提示:有什么方法建立数量关系?我们通常运用的方法是什么?看能不能运用勾股定理解决?4、发答题纸片,由学生完成,然后选做得好的同学的用展台进行展示,评讲师:(PPT9)由学生独立完成师:(PPT10)课堂小结切线长定理为证明线段相等,角相等,弧相等,垂直关系提供了理论依据。必须掌握并能灵活应用。2、希望同学们在以后的学习中要勇于探索和实践,养成科学的学习态度。同时还要注意总结作辅助线的方法和解题时要注意运用“数形结合”的思想方法。3、本堂课你学到些什么? 学生观看图,回顾切线长定理学生根据问题动手操作画出图形,独立思考,在老师的引导下完成。观看PPT4 回答问题1认真观察图形理解题目1、由学生完成,感受独立完成后的喜悦2. 根据老师的公式,产生好奇感,激发求知欲,进一步探索内角平分线夹角的公式和一个内角平分线和一外角平分线夹角的公式。学生思考,领会并记住公式,掌握解题技巧。学生认真观察图形掌握并能根据题目作出常用的辅助线,然后在图形中获取自己解题有用的信息。让学生感受一题多解的思想不同的思维方式可有不同的解题方法。让学生根据直角三角形内切圆半径的公式讨论一般三角形内切圆的半径公式认真观察图形,回答问题1掌握外延的相关知识知识的运用,根据上一题的讲解,掌握基本解题思路,及时运用到本题,得出结论通过学习提醒,提炼解题的基本思想,让学生掌握一定的解题思路。根据题目认真观察图形,首先打开解题思路,找到解题的方法,进行推理论证。积极讨论,发表意见然后在答题纸上开始答题,最先完成的,老师展台展示完成情况。学生口述切线长定理学生思考后发表意见,回答并总结 利用图形情景导入使学生能形象感知内容,为本节知识作准备学生动手操作,体会成功感,培养动手能力从实践到理论,知识来源于实践激发学生激情,主动认真思考并解决问题在探索过程中体验数学的快乐,把理论用于实践中去师生共同参与,培养了凝聚力激发学生的学习兴趣使学生养成观察、探索、探究、讨论、归纳的良好学习习惯,对知识的总结和积累培养学生的观察能力培养学生知识迁移的能力,灵活运用学过的解题方法得出结论,感受成功的喜悦。切线长定理的应用,在掌握基本解题思路和方法的同时,灵活的应用切线长定理解决数学问题。对学生独立完成作业后的肯定,激发学生独立完成作业的欲望,培养学生学习的自信心和成就感,养成良好的学习习惯。
板书设计 切线长定理切线长定理内容的两部分:一相等,二平分 关于三角形相关的角平分线的二级公式:900-1/2∠P,900+1/2∠x,1/2x直角三角形内切圆的半径公式r=(a+b-c)/2(切线长定理)直角三角形和一般三角形内切圆的半径公式:r=ab/(a+b+c)(面积法)
教学反思
.
O
D
E
C
B
A
P
F
E
D
C
B
A
O
.
C
B
A
O
.
O
A
B
C
D
E
C
P
A
B
D
O
A
同课章节目录
