2022-2023学年八年级数学下册北师大版 1.1.等腰三角形 同步练习(含答案)
文档属性
| 名称 | 2022-2023学年八年级数学下册北师大版 1.1.等腰三角形 同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 253.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-25 07:58:47 | ||
图片预览




文档简介
1.1. 等腰三角形
同步练习
一、单选题
1.如图,在等边△ABC中,AB=4cm,BD平分∠ABC,点E在BC的延长线上,且,则CE的长是( )
A.1cm B.2cm C.3cm D.4cm
2.如图,在中,,,,则( )
A. B. C. D.
3.如图,直线l1l2,点C、A分别在l1、l2上,以点C为圆心,CA长为半径画弧,交l1于点B,连接AB.若∠BCA=150°,则∠1的度数为( )
A.10° B.15° C.20° D.30°
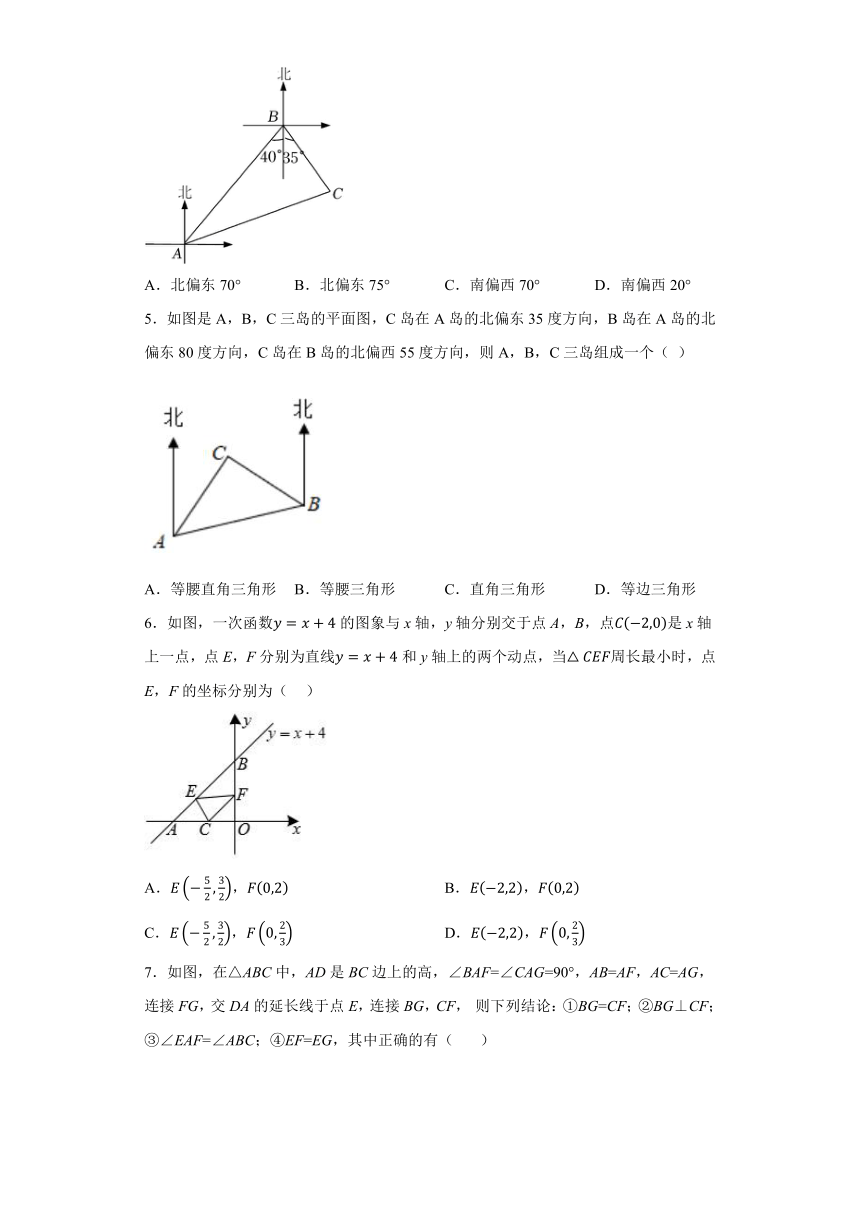
4.如图,某海域中有A,B,C三个小岛,其中A在B的南偏西40°方向,C在B的南偏东35°方向,且B,C到A的距离相等,则小岛C相对于小岛A的方向是( )
A.北偏东70° B.北偏东75° C.南偏西70° D.南偏西20°
5.如图是A,B,C三岛的平面图,C岛在A岛的北偏东35度方向,B岛在A岛的北偏东80度方向,C岛在B岛的北偏西55度方向,则A,B,C三岛组成一个( )
A.等腰直角三角形 B.等腰三角形 C.直角三角形 D.等边三角形
6.如图,一次函数的图象与x轴,y轴分别交于点A,B,点是x轴上一点,点E,F分别为直线和y轴上的两个动点,当周长最小时,点E,F的坐标分别为( )
A., B.,
C., D.,
7.如图,在△ABC中,AD是BC边上的高,∠BAF=∠CAG=90°,AB=AF,AC=AG,连接FG,交DA的延长线于点E,连接BG,CF, 则下列结论:①BG=CF;②BG⊥CF;③∠EAF=∠ABC;④EF=EG,其中正确的有( )
A.①②③ B.①②④ C.①③④ D.①②③④
8.如图所示,在四边形ABCD中,,,,,在AD上找一点P,使的值最小;则的最小值为( )
A.4 B.3 C.5 D.6
9.如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作等边△ABC和等边△ECD,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q连接PQ.以下五个结论正确的是( )
① ;②PQ∥AE; ③ ;④ ;⑤
A.①③⑤ B.①③④⑤ C.①②③⑤ D.①②③④⑤
10.如图,中,,点D在内部,且使得.则的度数为( )
A. B. C. D.不能确定
二、填空题
11.如图,在等边△ABC中,点E是边AC上一点,AD为BC边上的中线,AD、BE相交于点F,若∠AEB=100°,则∠AFB的度数为_____.
12.如图,在中,,点D为的中点,将绕点D逆时针旋转得到,当点A的对应点落在边上时,点在的延长线上,连接,若,则的面积是____________.
13.《庄子 天下篇》记载“一尺之锤,日取其半,万世不竭.”如图,直线与轴交于点,过点作轴的平行线交直线于点,过点作轴的平行线交直线于点,以此类推,令,,,,若对任意大于1的整数恒成立,则的最小值为___________.
14.如图,为等边的BC边上的高,E、F分别为线段上的动点,且,若时,则的最小值为_____,若时,的最小值为_____.
15.如图,在平面直角坐标系中,一次函数分别交x轴、y轴于A、B两点,若C为x轴上的一动点,则2BC+AC的最小值为__________.
三、解答题
16.为了解学生对所学知识的应用能力,某校老师在八年级数学兴趣小组活动中,设置了这样的问题:因为池塘两端A,B的距离无法直接测量,请同学们设计方案测量A,B的距离.甲、乙两位同学分别设计出了如下两种方案:
甲:如图1,先在平地上取一个可以直接到达点A,B的点O,连接AO并延长到点C,连接BO并延长到点D,使CO=AO,DO=BO,连接DC,测出DC的长即可;
乙:如图2,先确定直线AB,过点B作直线BE⊥AB,在直线BE上找可以直接到达点A的一点D,连接DA,作DC=DA,交直线AB于点C,最后测量BC的长即可.
甲、乙两个同学的方案是否可行?请说明理由.
17.如图,在△ABC中,∠A=100°,AB=AC,BE是∠ABC的平分线,求证:AE+BE=BC.
18.如图,E为的外角平分线上的一点,AE//BC,.
(1)求证:是等腰三角形;
(2)若,求CE的长.
19.在边长为9的等边三角形中,点是上一点,点是上一动点,以每秒1个单位的速度从点向点移动,设运动时间为秒.
(1)如图1,若,,求的值;
(2)如图2,若点从点向点运动,同时点以每秒2个单位的速度从点经点向点运动,当为何值时,为等边三角形?
20.如图1,中,,点D在AB上,且.
(1)求的大小;
(2)如图2,于E,于F,连接EF交CD于点H.
①求证:CD垂直平分EF:
②猜想三条线段AE,DB,BF之间的数量关系,并对你的猜想进行说明.
21.如图,直线与x轴、y轴分别交于点,点P在x轴上运动,连接,将沿直线折叠,点O的对应点记为.
(1)求k、b的值;
(2)在x轴上是否存在点C,使得为等腰三角形?若存在,求出点C的坐标;若不存在,说明理由.
(3)若点恰好落在直线上,求的面积.
参考答案:
1.B2.D3.B4.A5.A6.C7.D8.A9.C10.C
11.130度
12.
13.2
14.
15.6
16.甲、乙两同学的方案都可行
17.解:如图,延长BE到F,使BF=BC,连接FC,
∵AB=AC,∠A=100°,
∴∠ABC=∠ACB=40°,
∵BE平分∠ABC,
∴∠ABE=∠EBC=20°,
∵BF=BC,
∴∠F=∠BCF=80°,
∴∠FCE=∠ACB=40°,
在BC上取CF′=CF,连接EF′,
在△FCE与△F′CE中,,
∴△FCE≌△F′CE(SAS),
∴EF=EF′,∠EF′C=∠F=80°,
∴∠BF′E=100°,
∴∠A=∠BF′E,
在△ABE与△F′BE中,,
∴△ABE≌△F′BE(AAS),
∴AE=EF′,
∴AE=EF,
∴AE+BE=BE+EF=BC.
18.(1)证明:∵AE//BC,
,,
为的外角平分线上的一点,
,
,
,
是等腰三角形.
(2)解:由(1)已得:,
,
在和中,,
,
,
,
.
19.(1)3
(2)6
20.(1)解:设,
,
,
,
,
,
,
,
,
,
;
(2)①证明:由(1)得:,,
,
,,
,
,
,
,,
∴D点、C点均在EF是垂直平分线上,
∴CD垂直平分EF;
②三条线段AE,DB,BF之间的数量关系为:,理由如下:
在CA上截取,连接DG,如图2所示,
∵,
,,
,
,
,,
,
,
,,
由(1)得:,,
,
,
,
,
21.(1)
(2)存在,或或或
(3)或
同步练习
一、单选题
1.如图,在等边△ABC中,AB=4cm,BD平分∠ABC,点E在BC的延长线上,且,则CE的长是( )
A.1cm B.2cm C.3cm D.4cm
2.如图,在中,,,,则( )
A. B. C. D.
3.如图,直线l1l2,点C、A分别在l1、l2上,以点C为圆心,CA长为半径画弧,交l1于点B,连接AB.若∠BCA=150°,则∠1的度数为( )
A.10° B.15° C.20° D.30°
4.如图,某海域中有A,B,C三个小岛,其中A在B的南偏西40°方向,C在B的南偏东35°方向,且B,C到A的距离相等,则小岛C相对于小岛A的方向是( )
A.北偏东70° B.北偏东75° C.南偏西70° D.南偏西20°
5.如图是A,B,C三岛的平面图,C岛在A岛的北偏东35度方向,B岛在A岛的北偏东80度方向,C岛在B岛的北偏西55度方向,则A,B,C三岛组成一个( )
A.等腰直角三角形 B.等腰三角形 C.直角三角形 D.等边三角形
6.如图,一次函数的图象与x轴,y轴分别交于点A,B,点是x轴上一点,点E,F分别为直线和y轴上的两个动点,当周长最小时,点E,F的坐标分别为( )
A., B.,
C., D.,
7.如图,在△ABC中,AD是BC边上的高,∠BAF=∠CAG=90°,AB=AF,AC=AG,连接FG,交DA的延长线于点E,连接BG,CF, 则下列结论:①BG=CF;②BG⊥CF;③∠EAF=∠ABC;④EF=EG,其中正确的有( )
A.①②③ B.①②④ C.①③④ D.①②③④
8.如图所示,在四边形ABCD中,,,,,在AD上找一点P,使的值最小;则的最小值为( )
A.4 B.3 C.5 D.6
9.如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作等边△ABC和等边△ECD,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q连接PQ.以下五个结论正确的是( )
① ;②PQ∥AE; ③ ;④ ;⑤
A.①③⑤ B.①③④⑤ C.①②③⑤ D.①②③④⑤
10.如图,中,,点D在内部,且使得.则的度数为( )
A. B. C. D.不能确定
二、填空题
11.如图,在等边△ABC中,点E是边AC上一点,AD为BC边上的中线,AD、BE相交于点F,若∠AEB=100°,则∠AFB的度数为_____.
12.如图,在中,,点D为的中点,将绕点D逆时针旋转得到,当点A的对应点落在边上时,点在的延长线上,连接,若,则的面积是____________.
13.《庄子 天下篇》记载“一尺之锤,日取其半,万世不竭.”如图,直线与轴交于点,过点作轴的平行线交直线于点,过点作轴的平行线交直线于点,以此类推,令,,,,若对任意大于1的整数恒成立,则的最小值为___________.
14.如图,为等边的BC边上的高,E、F分别为线段上的动点,且,若时,则的最小值为_____,若时,的最小值为_____.
15.如图,在平面直角坐标系中,一次函数分别交x轴、y轴于A、B两点,若C为x轴上的一动点,则2BC+AC的最小值为__________.
三、解答题
16.为了解学生对所学知识的应用能力,某校老师在八年级数学兴趣小组活动中,设置了这样的问题:因为池塘两端A,B的距离无法直接测量,请同学们设计方案测量A,B的距离.甲、乙两位同学分别设计出了如下两种方案:
甲:如图1,先在平地上取一个可以直接到达点A,B的点O,连接AO并延长到点C,连接BO并延长到点D,使CO=AO,DO=BO,连接DC,测出DC的长即可;
乙:如图2,先确定直线AB,过点B作直线BE⊥AB,在直线BE上找可以直接到达点A的一点D,连接DA,作DC=DA,交直线AB于点C,最后测量BC的长即可.
甲、乙两个同学的方案是否可行?请说明理由.
17.如图,在△ABC中,∠A=100°,AB=AC,BE是∠ABC的平分线,求证:AE+BE=BC.
18.如图,E为的外角平分线上的一点,AE//BC,.
(1)求证:是等腰三角形;
(2)若,求CE的长.
19.在边长为9的等边三角形中,点是上一点,点是上一动点,以每秒1个单位的速度从点向点移动,设运动时间为秒.
(1)如图1,若,,求的值;
(2)如图2,若点从点向点运动,同时点以每秒2个单位的速度从点经点向点运动,当为何值时,为等边三角形?
20.如图1,中,,点D在AB上,且.
(1)求的大小;
(2)如图2,于E,于F,连接EF交CD于点H.
①求证:CD垂直平分EF:
②猜想三条线段AE,DB,BF之间的数量关系,并对你的猜想进行说明.
21.如图,直线与x轴、y轴分别交于点,点P在x轴上运动,连接,将沿直线折叠,点O的对应点记为.
(1)求k、b的值;
(2)在x轴上是否存在点C,使得为等腰三角形?若存在,求出点C的坐标;若不存在,说明理由.
(3)若点恰好落在直线上,求的面积.
参考答案:
1.B2.D3.B4.A5.A6.C7.D8.A9.C10.C
11.130度
12.
13.2
14.
15.6
16.甲、乙两同学的方案都可行
17.解:如图,延长BE到F,使BF=BC,连接FC,
∵AB=AC,∠A=100°,
∴∠ABC=∠ACB=40°,
∵BE平分∠ABC,
∴∠ABE=∠EBC=20°,
∵BF=BC,
∴∠F=∠BCF=80°,
∴∠FCE=∠ACB=40°,
在BC上取CF′=CF,连接EF′,
在△FCE与△F′CE中,,
∴△FCE≌△F′CE(SAS),
∴EF=EF′,∠EF′C=∠F=80°,
∴∠BF′E=100°,
∴∠A=∠BF′E,
在△ABE与△F′BE中,,
∴△ABE≌△F′BE(AAS),
∴AE=EF′,
∴AE=EF,
∴AE+BE=BE+EF=BC.
18.(1)证明:∵AE//BC,
,,
为的外角平分线上的一点,
,
,
,
是等腰三角形.
(2)解:由(1)已得:,
,
在和中,,
,
,
,
.
19.(1)3
(2)6
20.(1)解:设,
,
,
,
,
,
,
,
,
,
;
(2)①证明:由(1)得:,,
,
,,
,
,
,
,,
∴D点、C点均在EF是垂直平分线上,
∴CD垂直平分EF;
②三条线段AE,DB,BF之间的数量关系为:,理由如下:
在CA上截取,连接DG,如图2所示,
∵,
,,
,
,
,,
,
,
,,
由(1)得:,,
,
,
,
,
21.(1)
(2)存在,或或或
(3)或
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
