2022-2023学年 京改版九年级数学下册23.4位似变换课后专题练习(无答案)
文档属性
| 名称 | 2022-2023学年 京改版九年级数学下册23.4位似变换课后专题练习(无答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 413.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-25 10:33:39 | ||
图片预览


文档简介
23.4位似变换课后专题练习
班级:________ 姓名:________
一、单选题(共 10 小题)
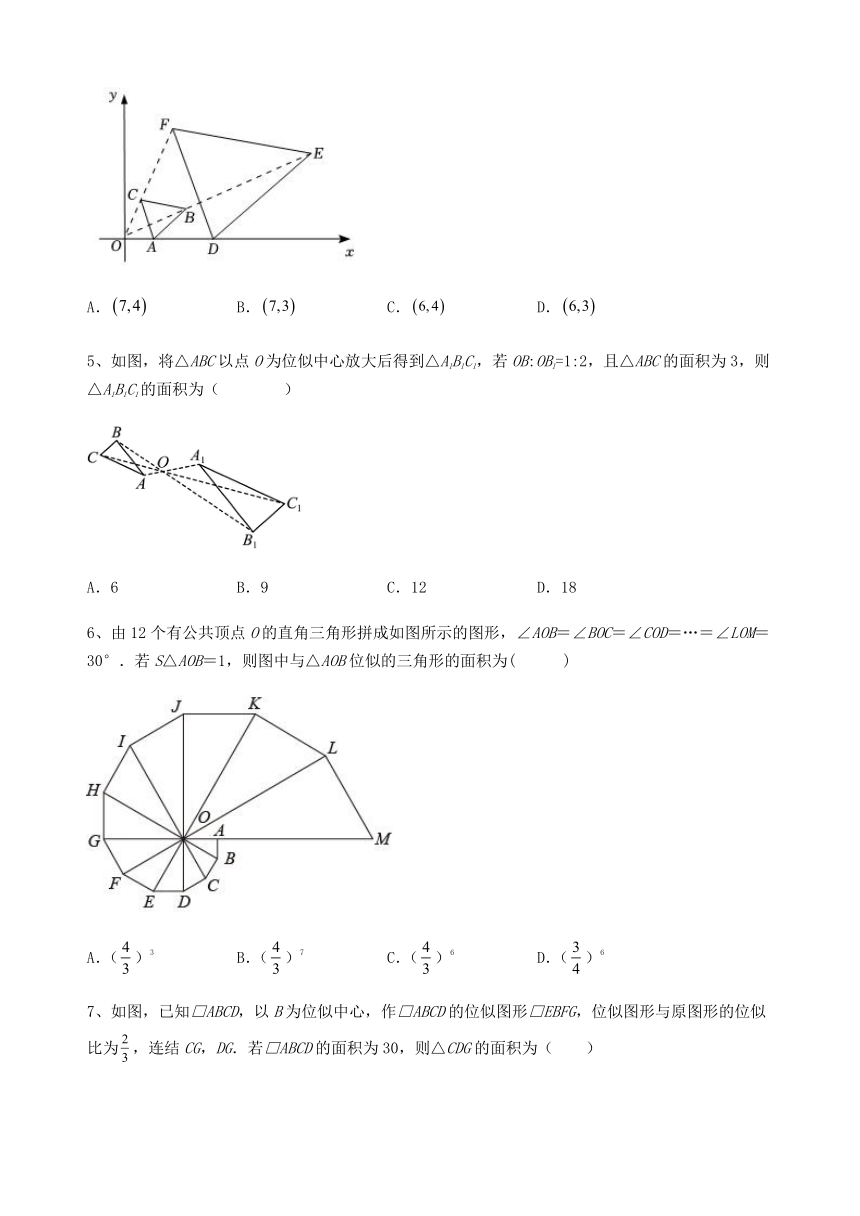
1、某学习小组在讨论“变化的三角形”时,知道大三角形与小三角形是位似图形(如图所示),则小三角形上的顶点(a,b)对应于大三角形上的顶点 ( )
A.(-2a,-2b) B.(2a,2b) C.(-2b,-2a) D.(-2a,-b)
2、如图,△AOB中,A,B两个顶点在x轴的上方,点O是原点.以点O为位似中心,在x轴的下方作△AOB的位似图形△A′OB′,且AB:A′B′=1:2.若点A的横坐标是a,则点A的对应点A′的横坐标是( )
A.﹣2a B.2a C. D.
3、已知△ABC中,AB=AC,∠A=36°,以点A为位似中心把△ABC的各边放大2倍后得到△AB′C′,则∠B的对应角∠B′的度数为( )
A.36° B.54° C.72° D.144°
4、如图,在平面直角坐标系中,已知,,,ABC与DEF位似,原点O是位似中心,则E点的坐标是( )
A. B. C. D.
5、如图,将△ABC以点O为位似中心放大后得到△A1B1C1,若OB:OB1=1:2,且△ABC的面积为3,则△A1B1C1的面积为( )
A.6 B.9 C.12 D.18
6、由12个有公共顶点O的直角三角形拼成如图所示的图形,∠AOB=∠BOC=∠COD=…=∠LOM=30°.若S△AOB=1,则图中与△AOB位似的三角形的面积为( )
A.()3 B.()7 C.()6 D.()6
7、如图,已知□ABCD,以B为位似中心,作□ABCD的位似图形□EBFG,位似图形与原图形的位似比为,连结CG,DG.若□ABCD的面积为30,则△CDG的面积为( )
A.3 B.4 C.5 D.6
8、下列命题:①两个正方形是位似图形;②两个等边三角形是位似图形;③两个同心圆是位似图形;④平行于三角形一边的直线截这个三角形的两边,所得的三角形与原三角形是位似图形,其中正确的有( )
A.1个 B.2个 C.3个 D.4个
9、如图,已知ABC,任取一点O,连AO,BO,CO,分别取点D,E,F,使OD=AO,OE=BO,OF=CO,得DEF.下列说法中,错误的是( )
A.DEF与ABC是位似三角形 B.OAC与ODF是位似三角形
C.DEF与ABC周长的比是1:3 D.图中位似的两个三角形面积比是1:9
10、△DEF和△ABC是位似图形,点O是位似中心,点D,E,F分别是OA,OB,OC的中点,若△DEF的面积是2,则△ABC的面积是( )
A.2 B.4 C.6 D.8
二、填空题(共 10 小题)
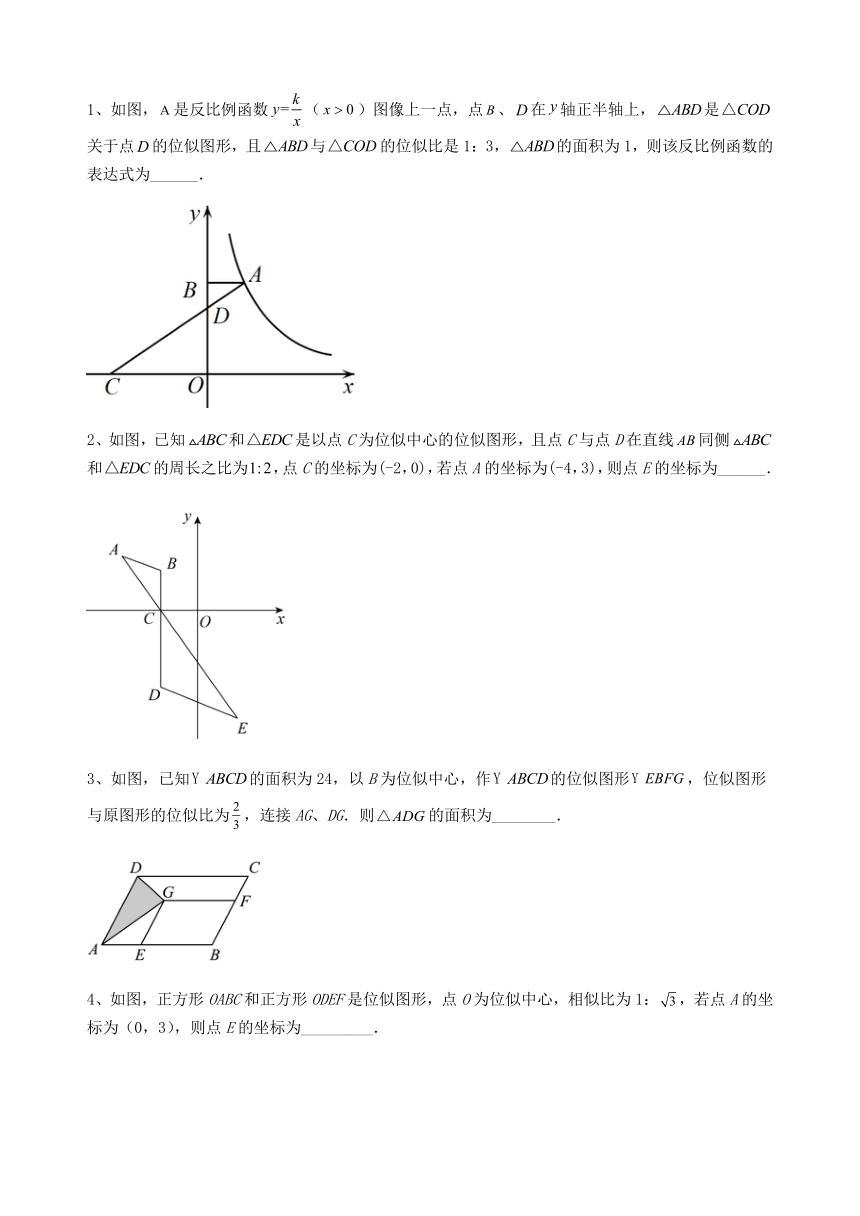
1、如图,是反比例函数()图像上一点,点、在轴正半轴上,是关于点的位似图形,且与的位似比是1:3,的面积为1,则该反比例函数的表达式为______.
2、如图,已知和是以点C为位似中心的位似图形,且点C与点D在直线同侧和的周长之比为,点C的坐标为(-2,0),若点A的坐标为(-4,3),则点E的坐标为______.
3、如图,已知的面积为24,以B为位似中心,作的位似图形,位似图形与原图形的位似比为,连接AG、DG.则的面积为________.
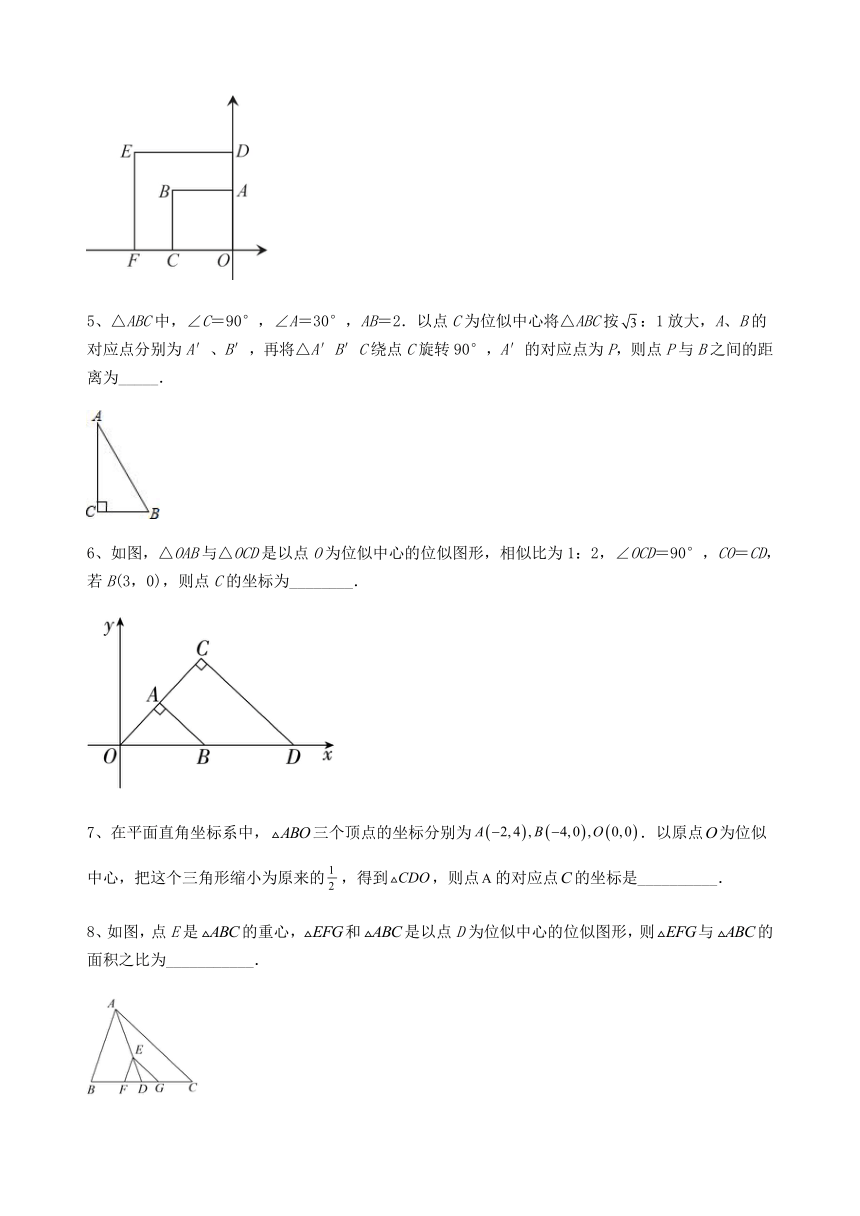
4、如图,正方形OABC和正方形ODEF是位似图形,点O为位似中心,相似比为1:,若点A的坐标为(0,3),则点E的坐标为_________.
5、△ABC中,∠C=90°,∠A=30°,AB=2.以点C为位似中心将△ABC按:1放大,A、B的对应点分别为A′、B′,再将△A′B′C绕点C旋转90°,A′的对应点为P,则点P与B之间的距离为_____.
6、如图,△OAB与△OCD是以点O为位似中心的位似图形,相似比为1:2,∠OCD=90°,CO=CD,若B(3,0),则点C的坐标为________.
7、在平面直角坐标系中,三个顶点的坐标分别为.以原点为位似中心,把这个三角形缩小为原来的,得到,则点的对应点的坐标是__________.
8、如图,点E是的重心,和是以点D为位似中心的位似图形,则与的面积之比为___________.
9、如图,线段CD两个端点的坐标分别为C(1,2)、D(2,0),以原点为位似中心,将线段CD放大得到线段AB,若点B坐标为(5,0),则点A的坐标为__________.
10、如图,与是位似图形,点是位似中心,若,,则________.
三、解答题(共 6 小题)
1、已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).
(1)△ABC向下平移4个单位长度得到的,点的坐标是 ;
(2)以点B为位似中心,在网格内画出,使与△ABC位似,且位似比为2:1,点的坐标是 ;(画出图形)
(3)的面积是 平方单位.
2、如图所示,在网格中,每个小正方形的边长均为1个单位长度,把小正方形的顶点叫做格点,为平面直角坐标系的原点,矩形的4个顶点均在格点上,连接对角线.
(1)在平面直角坐标系内,以原点为位似中心,把缩小,作出它的位似图形,并且使所作的位似图形与的相似比等于;
(2)将以为旋转中心,逆时针旋转,得到,作出,并求出线段旋转过程中所形成扇形的周长.
3、如图,在网格中,每个小正方形的边长为1个单位长度,AB是以格点(网格线的交点)为端点的线段,O是网格中一格点.
(1)将线段AB绕格点O顺时针旋转90°,得到线段CD(点A,B的对应点分别为点C,D),画出线段CD;
(2)以格点O为位似中心,在格点O的另一侧将放大为原来的2倍(即相似比为2∶1),得到,画出,并直接写出的面积.
4、在如图所示的方格中,△OAB的顶点坐标分别为O(0,0)、A(﹣2,﹣1)、B(﹣1,﹣3),△O1A1B1与△OAB是关于点P为位似中心的位似图形.
(1)在图中标出位似中心P的位置,并写出点P的坐标及△O1A1B1与△OAB的位似比;
(2)以原点O为位似中心,在y轴的左侧画出△OAB的另一个位似△OA2B2,使它与△OAB的位似比为2:1,并写出点B的对应点B2的坐标.
5、如图,在平面直角坐标系中,的三个顶点坐标分别是,,.
(1)将向左平移4个单位长度后得到,请画出;
(2)以点为位似中心,在轴的左侧画出的位似图形,使与的位似比为1:2;
(3)请直接写出的值.
6、将下图中的△ABC作下列变换,画出相应的图形,指出三个顶点的坐标所发生的变化.
(1)沿y轴负方向平移1个单位;
(2)关于x轴对称;
(3)以C点为位似中心,放大到1.5倍.
班级:________ 姓名:________
一、单选题(共 10 小题)
1、某学习小组在讨论“变化的三角形”时,知道大三角形与小三角形是位似图形(如图所示),则小三角形上的顶点(a,b)对应于大三角形上的顶点 ( )
A.(-2a,-2b) B.(2a,2b) C.(-2b,-2a) D.(-2a,-b)
2、如图,△AOB中,A,B两个顶点在x轴的上方,点O是原点.以点O为位似中心,在x轴的下方作△AOB的位似图形△A′OB′,且AB:A′B′=1:2.若点A的横坐标是a,则点A的对应点A′的横坐标是( )
A.﹣2a B.2a C. D.
3、已知△ABC中,AB=AC,∠A=36°,以点A为位似中心把△ABC的各边放大2倍后得到△AB′C′,则∠B的对应角∠B′的度数为( )
A.36° B.54° C.72° D.144°
4、如图,在平面直角坐标系中,已知,,,ABC与DEF位似,原点O是位似中心,则E点的坐标是( )
A. B. C. D.
5、如图,将△ABC以点O为位似中心放大后得到△A1B1C1,若OB:OB1=1:2,且△ABC的面积为3,则△A1B1C1的面积为( )
A.6 B.9 C.12 D.18
6、由12个有公共顶点O的直角三角形拼成如图所示的图形,∠AOB=∠BOC=∠COD=…=∠LOM=30°.若S△AOB=1,则图中与△AOB位似的三角形的面积为( )
A.()3 B.()7 C.()6 D.()6
7、如图,已知□ABCD,以B为位似中心,作□ABCD的位似图形□EBFG,位似图形与原图形的位似比为,连结CG,DG.若□ABCD的面积为30,则△CDG的面积为( )
A.3 B.4 C.5 D.6
8、下列命题:①两个正方形是位似图形;②两个等边三角形是位似图形;③两个同心圆是位似图形;④平行于三角形一边的直线截这个三角形的两边,所得的三角形与原三角形是位似图形,其中正确的有( )
A.1个 B.2个 C.3个 D.4个
9、如图,已知ABC,任取一点O,连AO,BO,CO,分别取点D,E,F,使OD=AO,OE=BO,OF=CO,得DEF.下列说法中,错误的是( )
A.DEF与ABC是位似三角形 B.OAC与ODF是位似三角形
C.DEF与ABC周长的比是1:3 D.图中位似的两个三角形面积比是1:9
10、△DEF和△ABC是位似图形,点O是位似中心,点D,E,F分别是OA,OB,OC的中点,若△DEF的面积是2,则△ABC的面积是( )
A.2 B.4 C.6 D.8
二、填空题(共 10 小题)
1、如图,是反比例函数()图像上一点,点、在轴正半轴上,是关于点的位似图形,且与的位似比是1:3,的面积为1,则该反比例函数的表达式为______.
2、如图,已知和是以点C为位似中心的位似图形,且点C与点D在直线同侧和的周长之比为,点C的坐标为(-2,0),若点A的坐标为(-4,3),则点E的坐标为______.
3、如图,已知的面积为24,以B为位似中心,作的位似图形,位似图形与原图形的位似比为,连接AG、DG.则的面积为________.
4、如图,正方形OABC和正方形ODEF是位似图形,点O为位似中心,相似比为1:,若点A的坐标为(0,3),则点E的坐标为_________.
5、△ABC中,∠C=90°,∠A=30°,AB=2.以点C为位似中心将△ABC按:1放大,A、B的对应点分别为A′、B′,再将△A′B′C绕点C旋转90°,A′的对应点为P,则点P与B之间的距离为_____.
6、如图,△OAB与△OCD是以点O为位似中心的位似图形,相似比为1:2,∠OCD=90°,CO=CD,若B(3,0),则点C的坐标为________.
7、在平面直角坐标系中,三个顶点的坐标分别为.以原点为位似中心,把这个三角形缩小为原来的,得到,则点的对应点的坐标是__________.
8、如图,点E是的重心,和是以点D为位似中心的位似图形,则与的面积之比为___________.
9、如图,线段CD两个端点的坐标分别为C(1,2)、D(2,0),以原点为位似中心,将线段CD放大得到线段AB,若点B坐标为(5,0),则点A的坐标为__________.
10、如图,与是位似图形,点是位似中心,若,,则________.
三、解答题(共 6 小题)
1、已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).
(1)△ABC向下平移4个单位长度得到的,点的坐标是 ;
(2)以点B为位似中心,在网格内画出,使与△ABC位似,且位似比为2:1,点的坐标是 ;(画出图形)
(3)的面积是 平方单位.
2、如图所示,在网格中,每个小正方形的边长均为1个单位长度,把小正方形的顶点叫做格点,为平面直角坐标系的原点,矩形的4个顶点均在格点上,连接对角线.
(1)在平面直角坐标系内,以原点为位似中心,把缩小,作出它的位似图形,并且使所作的位似图形与的相似比等于;
(2)将以为旋转中心,逆时针旋转,得到,作出,并求出线段旋转过程中所形成扇形的周长.
3、如图,在网格中,每个小正方形的边长为1个单位长度,AB是以格点(网格线的交点)为端点的线段,O是网格中一格点.
(1)将线段AB绕格点O顺时针旋转90°,得到线段CD(点A,B的对应点分别为点C,D),画出线段CD;
(2)以格点O为位似中心,在格点O的另一侧将放大为原来的2倍(即相似比为2∶1),得到,画出,并直接写出的面积.
4、在如图所示的方格中,△OAB的顶点坐标分别为O(0,0)、A(﹣2,﹣1)、B(﹣1,﹣3),△O1A1B1与△OAB是关于点P为位似中心的位似图形.
(1)在图中标出位似中心P的位置,并写出点P的坐标及△O1A1B1与△OAB的位似比;
(2)以原点O为位似中心,在y轴的左侧画出△OAB的另一个位似△OA2B2,使它与△OAB的位似比为2:1,并写出点B的对应点B2的坐标.
5、如图,在平面直角坐标系中,的三个顶点坐标分别是,,.
(1)将向左平移4个单位长度后得到,请画出;
(2)以点为位似中心,在轴的左侧画出的位似图形,使与的位似比为1:2;
(3)请直接写出的值.
6、将下图中的△ABC作下列变换,画出相应的图形,指出三个顶点的坐标所发生的变化.
(1)沿y轴负方向平移1个单位;
(2)关于x轴对称;
(3)以C点为位似中心,放大到1.5倍.
