完全平方公式_2[下学期]
图片预览


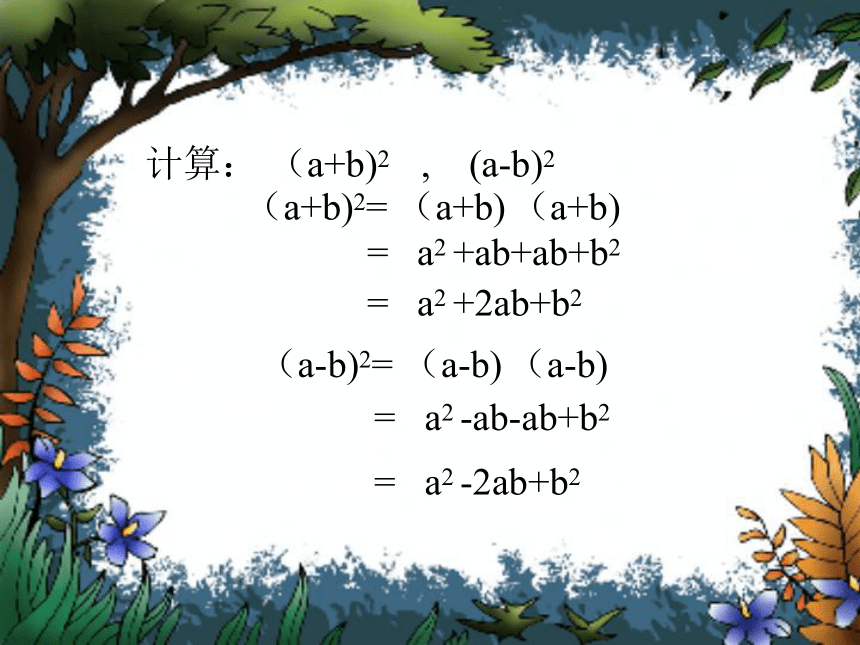


文档简介
课件15张PPT。CAI课件完全平方公式二00一年六月1002=10 0002002=40 0001022=10 4041992=39 601(-b+a)2=(a-b)2=[(-b)+a]2(-a-b)2=[(-a)+(-b)]2=[(-a)-b]2计算: (a+b)2 , (a-b)2(a+b)2= (a+b) (a+b)= a2 +ab+ab+b2= a2 +2ab+b2(a-b)2= (a-b) (a-b)= a2 -ab-ab+b2= a2 -2ab+b2完全平方公式(a+b)2=a2+2ab+b2 两数和(或差)的平方,等于这两个数平方的和,加上(或者减去)它们的积的2倍。(a- b)2=a2- 2ab+b2
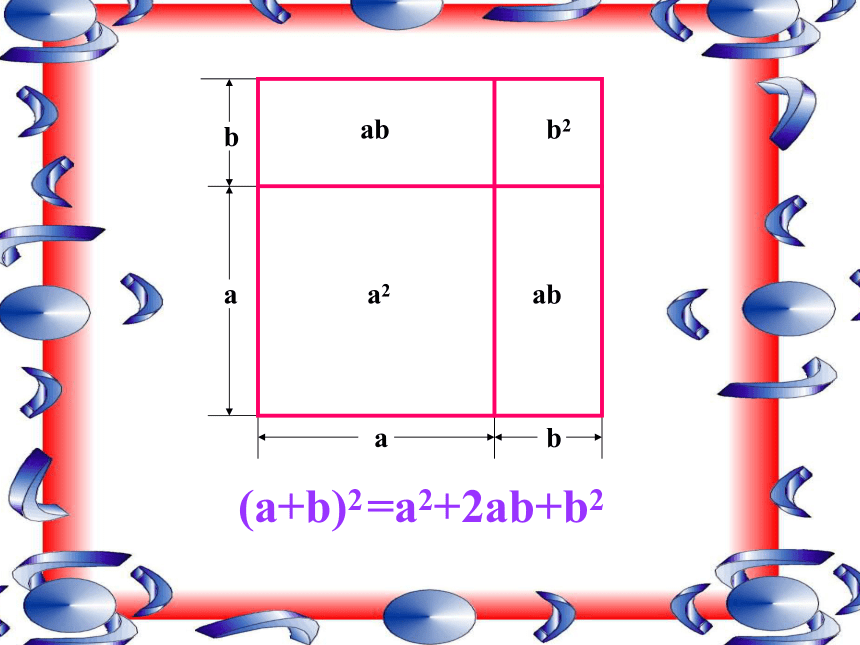
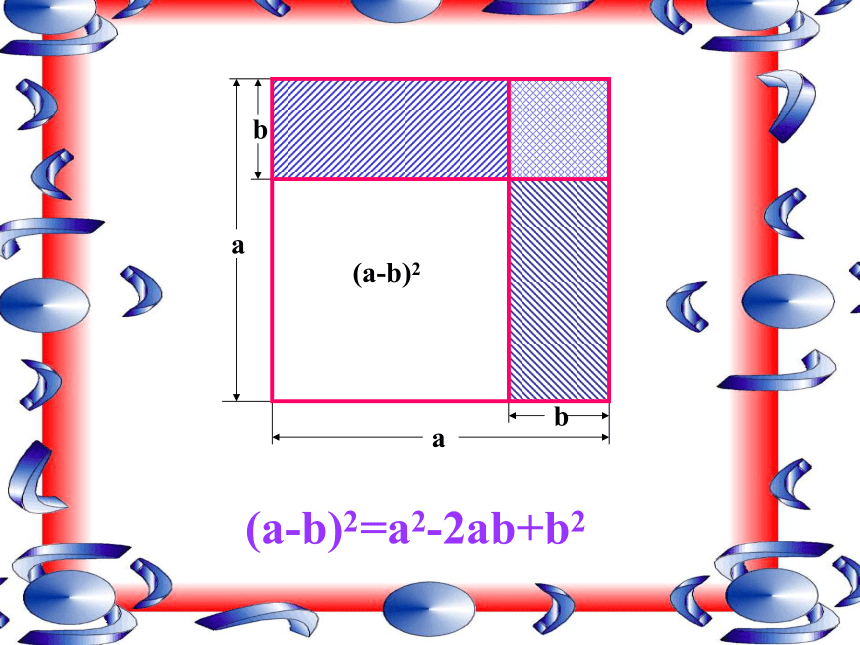
a2 ababb2baab(a+b)2=a2+2ab+b2abab(a-b)2(a-b)2=a2-2ab+b2完全平方公式(a+b)2=a2+2ab+b2(a- b)2=a2- 2ab+b2
口诀:首平方,尾平方,首尾两倍在中央。(x+2y)2 =+2 ? x ? 2y (a+b)2 = a2 +2 a b + b2= x2+4xy+4y2x2+(2y)2计算:(2x-3y)2 = (a - b)2 = a2 - 2 a b + b2(2x)2-2 ? 2x ? 3y+(3y)2=4x2-12xy+9y2例1 运用完全平方公式计算:(1) (4a-b)2解:(4a-b)2==16a2(2)解:(4a)2-2?4a?b+b2-8ab+b2+y= y2+例2 运用完全平方公式计算:(1) 1022解: 1022=(100+2)2=1002+2×100×2+22=10 000+400+4=10 404(2) 1992解: 1992=(200-1)2=2002-2×200+12=40 000 - 400+1=39 601课堂练习 (1)(a+6)2 (2)(4+x)2=a2+12a+36=16+8x+x2(3)(x-7)2 (4) (8-y)2
=x2-14x+49=64-16y+y2(5)(3a+b)2 (6)(4x+3y)2=9a2+6ab+b2=16x2+24xy+9y2(7)(-2x+5y)2(8)(-a-b)2
=4x2-20xy+25y2=a2+2ab+b21. 运用完全平方公式计算 : 课堂练习 :2. 运用完全平方公式计算 :(1)912
(2)3012=(90+1)2=8 281=(300+1)2=90 601(3)4982
(4)79.82=(500-2)2=248 004=(80-0.2)2=6 368.043.下面各式的计算错在哪里?应怎样改正?(1)(a+b)2=a2+b2(2)(a-b)2=a2-b2 想一想:
(a+b)2与(-a-b)2相等吗?
( a-b)2与(b-a)2也相等吗?
为什么?∵ (a+b)2=a2+2ab+b2(-a-b)2=(-a)2+2(-a)(-b)+(-b) 2=a2+2ab+b2∵ (a-b)2=a2-2ab+b2(b-a)2=b2-2ba+a2=a2-2ab+b2∴ (a+b)2= (-a-b)2∴ (a-b)2=(b-a)2本节小结4 应用完全平方公式计算时,要注意: (1)切勿把此公式与公式(ab)2= a2b2混淆,而随意写成(a+b)2 =a2 +b2(2)切勿把“乘积项”2ab中的2丢掉.1 回顾完全平方公式及其特点。2 公式中字母的含义。 3 在应用完全平方公式时,是用“和”还是用“差”,应具体对待,灵活运用。作业:
1 熟记完全平方公式
2 课本 P133:
1,2,3,
a2 ababb2baab(a+b)2=a2+2ab+b2abab(a-b)2(a-b)2=a2-2ab+b2完全平方公式(a+b)2=a2+2ab+b2(a- b)2=a2- 2ab+b2
口诀:首平方,尾平方,首尾两倍在中央。(x+2y)2 =+2 ? x ? 2y (a+b)2 = a2 +2 a b + b2= x2+4xy+4y2x2+(2y)2计算:(2x-3y)2 = (a - b)2 = a2 - 2 a b + b2(2x)2-2 ? 2x ? 3y+(3y)2=4x2-12xy+9y2例1 运用完全平方公式计算:(1) (4a-b)2解:(4a-b)2==16a2(2)解:(4a)2-2?4a?b+b2-8ab+b2+y= y2+例2 运用完全平方公式计算:(1) 1022解: 1022=(100+2)2=1002+2×100×2+22=10 000+400+4=10 404(2) 1992解: 1992=(200-1)2=2002-2×200+12=40 000 - 400+1=39 601课堂练习 (1)(a+6)2 (2)(4+x)2=a2+12a+36=16+8x+x2(3)(x-7)2 (4) (8-y)2
=x2-14x+49=64-16y+y2(5)(3a+b)2 (6)(4x+3y)2=9a2+6ab+b2=16x2+24xy+9y2(7)(-2x+5y)2(8)(-a-b)2
=4x2-20xy+25y2=a2+2ab+b21. 运用完全平方公式计算 : 课堂练习 :2. 运用完全平方公式计算 :(1)912
(2)3012=(90+1)2=8 281=(300+1)2=90 601(3)4982
(4)79.82=(500-2)2=248 004=(80-0.2)2=6 368.043.下面各式的计算错在哪里?应怎样改正?(1)(a+b)2=a2+b2(2)(a-b)2=a2-b2 想一想:
(a+b)2与(-a-b)2相等吗?
( a-b)2与(b-a)2也相等吗?
为什么?∵ (a+b)2=a2+2ab+b2(-a-b)2=(-a)2+2(-a)(-b)+(-b) 2=a2+2ab+b2∵ (a-b)2=a2-2ab+b2(b-a)2=b2-2ba+a2=a2-2ab+b2∴ (a+b)2= (-a-b)2∴ (a-b)2=(b-a)2本节小结4 应用完全平方公式计算时,要注意: (1)切勿把此公式与公式(ab)2= a2b2混淆,而随意写成(a+b)2 =a2 +b2(2)切勿把“乘积项”2ab中的2丢掉.1 回顾完全平方公式及其特点。2 公式中字母的含义。 3 在应用完全平方公式时,是用“和”还是用“差”,应具体对待,灵活运用。作业:
1 熟记完全平方公式
2 课本 P133:
1,2,3,
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
